静电场中等效法的应用

王彦斌

(甘肃省张掖市肃南裕固族自治县第一中学)

等效法是指将一个复杂的物理问题,等效转化为一个熟知的物理模型或问题的方法.常见的等效法有“分解”“等效类比”“等效简化”“等效变换”等.利用等效法解题,可以化繁为简,化难为易,达到事半功倍的效果.

1 在求电场强度中的应用

电场强度是高考重要考点之一,求解电场强度时,叠加法是最常用的方法,即空间某点存在几种电场时,利用几个电场强度的矢量合成求合电场.当场源电荷很多,或场源电荷的电场不好求解时,往往可利用等效法求解.

例1 如 图1 所 示,16 个电荷量均为＋q(q＞0)的小球(可视为点电荷),均匀分布在半径为R的圆周上.若将圆周上P点的一个小球的电荷量换成－2q,则圆心O点处的电场强度的大小为( ).

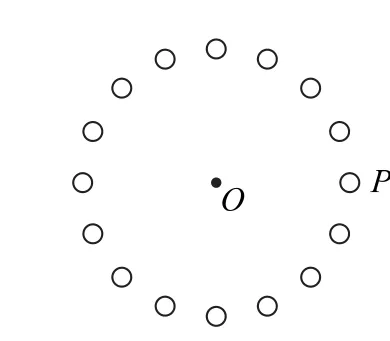
图1

例2 如图2所示,A、B、C、D、E是正五角星的五个尖端,O为五角星的中心,P点位于OA的连线上,且OA＝AP.在A、B、C、D、E五个点上各固定一个点电荷,除A点处的电荷量为－Q外,其余各点的电荷量均为＋Q,此时O点的场强大小为E,现将A点的负电荷移到P点,则O点的场强( ).

解决本题应用“等效类比”,即把A点处的电荷量换为＋Q,求得另外4个正电荷在O点的场强.

2 在求电势中的应用

电势是标量,电势叠加满足简单的代数运算.高中阶段没有给出电势的决定式,高考中对电势的考查,往往给出实际的情境,要求利用思维转化实现问题的巧妙求解.

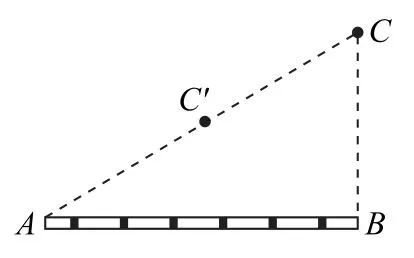
图3

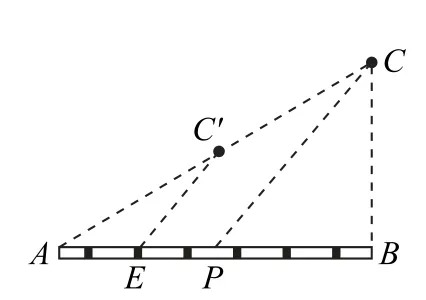
图4

3 在复合场中的应用

实际问题中,重力与电场力同时存在,且都对研究物体做功,则问题的求解过程会比较复杂.如果能将重力场和电场叠加而成的复合场等效为“重力场”,重力与电场力的合力等效为“重力”,将在只有重力存在的单一场下的解题思路、公式、方法、技巧运用到复合场中,可使题目得到相应的简化,实现问题的求解.

例4 如图5所示,在竖直向上的匀强电场中有一竖直放置的光滑半圆形绝缘轨道QPN与一水平绝缘轨道MN在N点平滑相接,半圆形轨道半径R＝40cm,N为半圆形轨道最低点,P为QN圆弧的中点,一带电荷量q＝－1×10－4C、质量为m＝10g的小滑块从N点右侧1.5 m 的M处以初速度v0＝7m·s－1向左运动,通过P点时对轨道的压力大小为0.6N,且小滑块恰能运动到圆弧轨道的最高点Q,g取10m·s－2,求电场强度的大小E以及小滑块与水平轨道间的动摩擦因数μ.

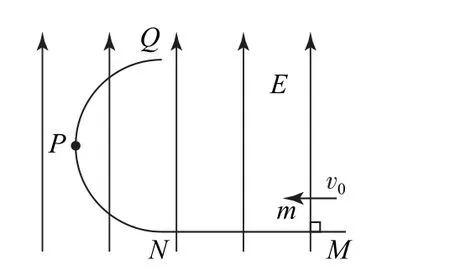
图5

分析 把电场力和重力的合力看成一个力,即有

联立方程解得E＝1×103V·m－1,μ＝0.15.

不用等效的办法,电场力和重力是两个力,列式烦琐、运算量大,利用“等效简化”,通过等效场把一个复合场中的问题转化为力学问题,思路简单,运算量少.

静电场问题是每年高考中的必考知识,等效法是求解静电场问题的一种重要思想方法,利用等效法可以化繁为简,起到事半功倍、立竿见影之效果.