基于细观有限元PVA-ECC材料基本力学性能研究
吴 少 峰
(福建省高速公路科技创新研究院有限公司,福建 福州 350000)
混凝土基础设施在长期外界环境的作用下,由于其固有的脆性,混凝土会不可避免的产生裂缝,从而引起混凝土内部钢筋的锈蚀,使得混凝土结构的使用寿命大幅下降。为了提高混凝土基础设施的耐久性和可持续性,延长其使用寿命,减少维修工作,提出了耐久性优良的工程基复合材料ECC(Engineered cementitious composite)[1]。ECC在拉伸荷载作用下表现出优良的韧性,其拉应变可以达到3%以上,是普通混凝土的几百倍。目前,国内外学者已对ECC做了大量的试验研究,包括ECC材料的抗拉性能,抗压性能,抗弯性能、耐久性等方面[2-4]。然而,这些研究都局限在试验方面,试验过程耗时耗力,试件养护以及龄期等因素带来的影响会对ECC材料的发展形成阻碍,因此很有必要从数值模拟的角度对ECC材料进行研究。
ECC材料的数值模拟可以分为宏观上的数值模拟和细观上的数值模拟,现阶段已有大量的学者进行了宏观尺度上的模拟,Bora Gencturk等[5]采用了宏观数值模型模拟ECC在循环荷载作用下的受力性能,并与试验的结果进行了比较,与试验的结果较为契合,证明了该模型的正确性。李晓琴等[6]运用有限元软件ABAQUS对ECC框架节点在低周往复荷载作用的受力性能进行了数值模拟。然而想要从更深层次上的了解ECC材料,还必须从细观尺度上进行模拟。现阶段,已有学者对混凝土以及钢纤维混凝土的细观数值模拟展开研究,徐彬[7]通过MATLAB实现了混凝土骨料的随机投放算法,建立了纤维混凝土的细观几何模型,为后续通过细观有限元研究混凝土的力学性能奠定了基础。张慧[8]提出了离散-连续耦合细观有限元模型,采用MATLAB实现了零厚度粘结单元的生成算法,模拟钢纤维与基体之间的粘结滑移。并用此模型建立了带缺口试件的直接拉伸、UHPFR从带缺口试件的三点弯与UHPFRC无缺口构件,并通过细观有限元模型研究了各试件的细观破坏机理。Xu等[9]利用ANSYS有限元软件建立了纤维、骨料、基体组成的二维三相细观模型,并利用LS-DYNA有限元软件对冲击荷载作用下的细观有限元模型进行研究。Liang等[10]基于Delaunay三角剖分,成功地建立并验证了钢纤维混凝体的三维细观模型。而相对于钢纤维混凝土的细观数值模拟,ECC材料中PVA纤维直径小、数量多,会对纤维在基体中的随机投放带来一定的挑战,同时PVA纤维与基体之间有着更为复杂的粘结滑移关系。
在前人钢纤维混凝土的细观数值模拟的基础上对ECC材料的细观数值建模展开研究,采用Python语言实现PVA纤维在基体中的随机分布,将ECC看作是由纤维、基体构成的二相非均质材料,模拟ECC材料的非均质性,并考虑纤维与基体之间的相互作用,建立细观尺度下的ECC有限元模型,分析有限元模型在拉、压状态下的力学性能,并和已有的试验结果进行比较研究模型的有效性。从而通过细观数值模拟揭示ECC材料在荷载作用下的力学性能以及内部损伤破坏情况。
1 PVA纤维随机投放算法研究
ECC在浇筑制作过程中,需要将PVA纤维随机分散在基体中,需要严格避免纤维结团以及分散不均匀的情况发生,只有这样才能充分发挥PVA纤维在ECC材料中的作用。因此,在进行ECC材料的细观有限元模拟过程中,不仅仅要模拟ECC材料中的各相组成材料基体以及纤维,还要实现纤维在基体中的随机分布。
与钢纤维不同,有机纤维较细。在ECC材料的细观模拟中,ECC材料中庞大的纤维数量往往给数值模拟带来一定的挑战。因此,为了简化模型,提高计算效率,通常将三维的模型简化为二维的模型。本文将纤维简化为线条,利用Python语言实现二维的线状纤维在二维基体中的随机生成与投放。其中纤维数量n的计算公式为:
(1)
式中:a、b为基体的长度、宽度;Vf为纤维体积分数;d、l为纤维的直径和长度。
二维线状纤维的投放过程中,纤维的控制参数有纤维的中心点坐标以及纤维的倾角,利用Python语言提供的Numpy模块随机生成一根纤维的中心点坐标以及纤维的倾角,即可确定纤维的位置。根据纤维的长度就可推算出纤维两端点的坐标,并且保证纤维的端点都在基体范围内。
如图1所示,首先确定AB纤维的中心点O的坐标(xi,yi),根据纤维的长度以及纤维的倾角确定纤维两端点A、B的坐标。端点的具体坐标可表示为:
(2)
(3)
(4)
(5)
在随机生成所有纤维的端点坐标后,利用ABAQUS二次开发接口提供的Line()几何建模方法,将所有PVA纤维的两个端点坐标连成直线,从而得到纤维随机投放的几何模型。
利用上述介绍的程序算法生成ECC受压构件的纤维随机投放模型,基体的平面尺寸为70.7 mm×70.7 mm,纤维的数量采用公式(1)确定,经过计算,纤维体积分数为1.5%、2.0%、2.5%的试件纤维数量分别为157根、209根、261根。各纤维体积分数的纤维投放图如图2所示,从图2中可以看出,纤维随机分布在基体中,满足规定的投放原则,验证了本文程序算法的正确性和可靠性。
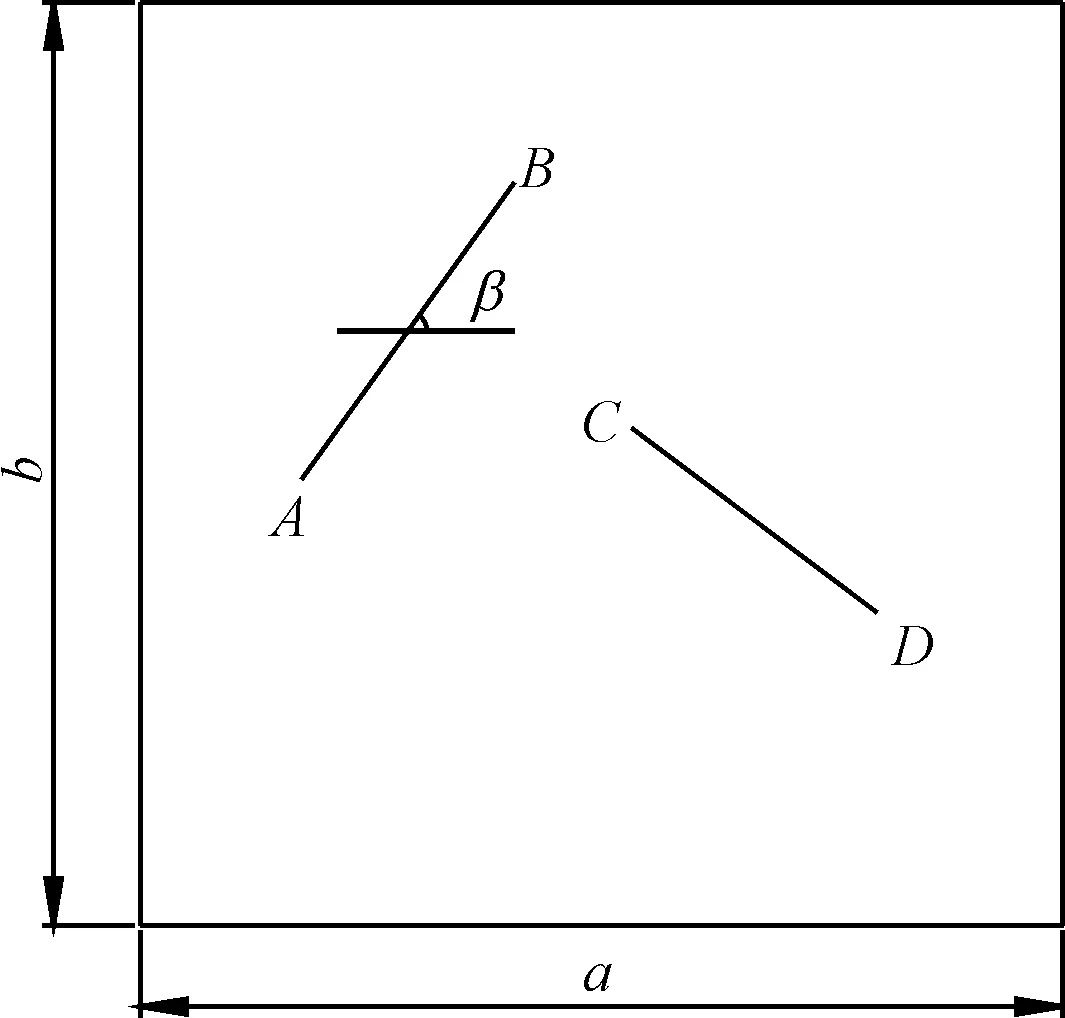
图1 纤维的投放意示图

图2 各纤维体积分数的纤维随机投放
2 数值模拟
2.1 PVA纤维本构
在ECC的细观有限元模拟过程中,PVA纤维采用线弹性本构来进行模拟,纤维的参数见表1所示,纤维达到其极限抗拉强度后即发生断裂,然而要想实现ECC的拉伸应变硬化,纤维的断裂对应力的传递非常不利,纤维的拔出而非拔断才能实现ECC材料的拉伸应变硬化。因此,在达到纤维的极限抗拉强度之前,纤维往往已经从基体中拔出,纤维与基体之间的粘结滑移本构起控制作用。

表1 国产PVA纤维的基本性能
2.2 基体本构
在ABAQUS有限元软件模拟中,混凝土的本构一般采用混凝土塑性损伤模型。对于基体的本构,文献[11-12]表明混凝土的力学性能与水泥砂浆类似,采用混凝土塑性损伤模型来模拟基体。
有限元模拟中的基体强度采用立方体试件的试验实测抗压强度,其数值为29.48 MPa,抗拉强度为3.05 MPa,弹性模量取30 GPa,泊松比为0.2,密度取为2.0 kg/cm3。在ABAQUS有限元软件中,需要给出塑性损伤模型中一些特殊的参数来定义基体的屈服及破坏准则,具体参数的取值参见表2。

表2 塑性损伤模型中的一些特殊参数
2.3 PVA纤维与基体之间的粘结滑移本构
通过Li[12]提出的PVA纤维与基体之间的粘结滑移本构模型来模拟纤维与基体之间的相互作用。三个微观参数由单纤维拉拔试验所得的粘结滑移曲线确定,试验基体尺寸采用10 mm×310 mm×310 mm,纤维埋深为1 mm,单纤维拉拔试验加载过程见图3,具体数据如表3所示。

图3 PVA单纤维拉拔试验
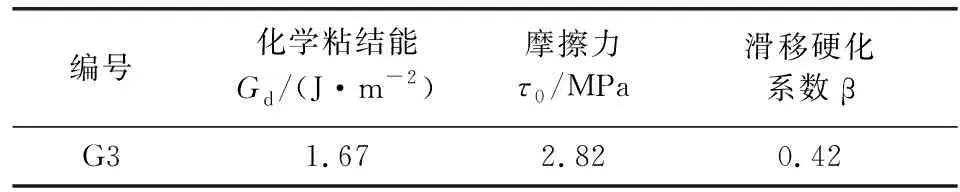
表3 G3的微观参数
张鹏[13]将纤维与基体之间的粘结滑移本构模型赋予纤维单元,在建模过程中不考虑纤维与基体之间的相互作用,而是将纤维嵌入到基体中。把PVA纤维与基体粘结滑移作用等效为纤维的拉伸作用,其本构关系由纤维与基体之间的粘结滑移本构换算得出,具体表达为:
(6)
(7)
式中:σf、εf分别为纤维的应力与应变;P、Sf为PVA纤维的拉拔荷载以及纤维的滑移长度;D、Lf为纤维的直径以及纤维的长度。
对于Li提出的单纤维拉拔模型,纤维的埋深是影响纤维与基体之间的粘结性能的重要因素。然而对于细观数值模拟方法,通常无法预先判断基体的开裂位置,纤维的埋深无法预知。纤维长度为12 mm的纤维,埋深在0 mm~6 mm范围内的单纤维拉拔模型如图4所示,可以看到埋深为2 mm的纤维更接近平均化后的粘结滑移本构,因此本文的细观有限元模型中采用纤维埋深为2 mm的粘结滑移本构。埋深为4 mm、5 mm、6 mm的纤维在脱粘阶段就发生了断裂,为了更好的实现纤维在断裂过程中纤维的拉拔力突然下降的效果,但纤维的接近断裂时,拔出荷载取为0.05 N。为了简化模型,本文暂不考虑纤维与基体之间的夹角对纤维拉拔本构的影响。
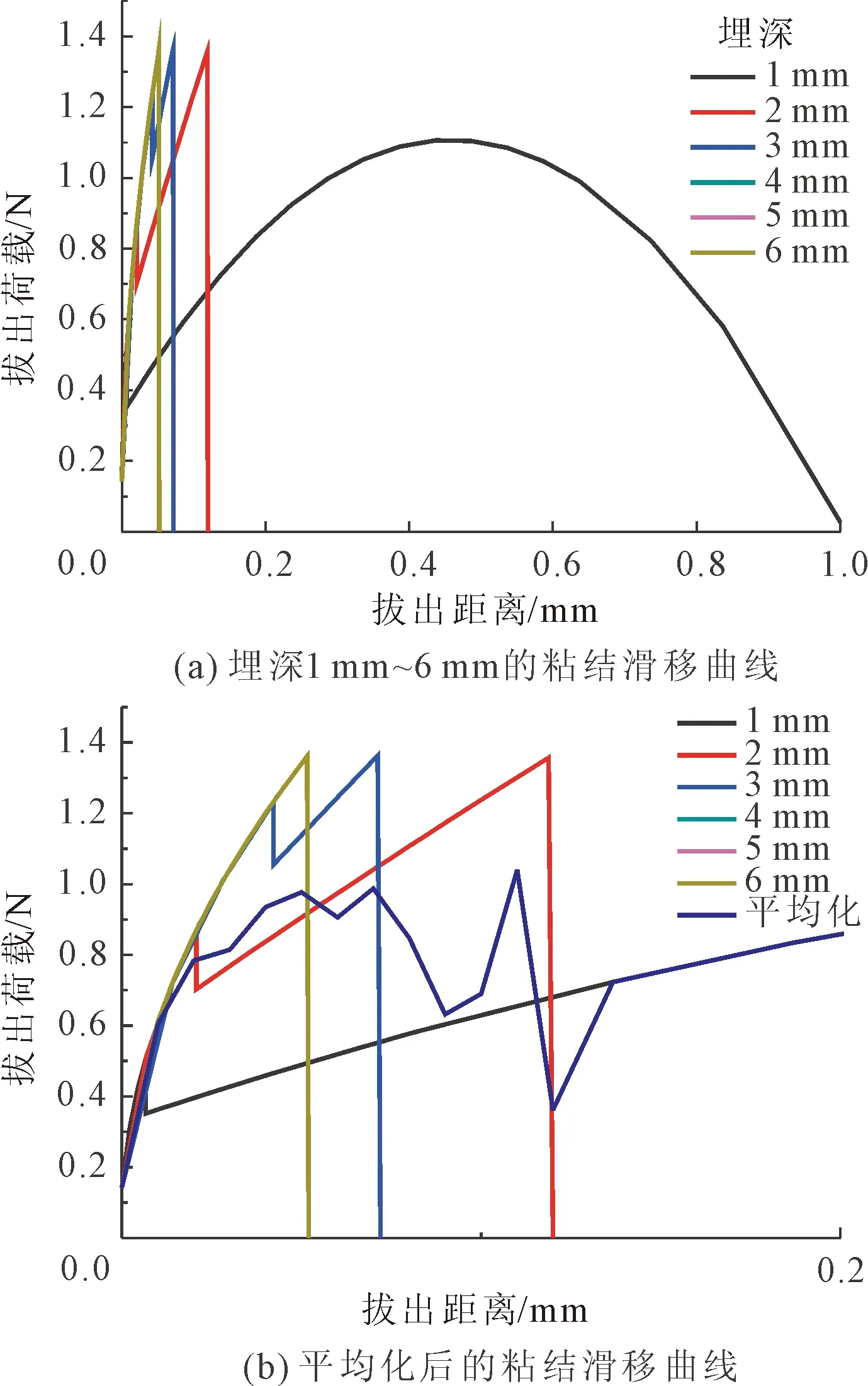
图4 埋深为1 mm~6 mm的粘结滑移曲线及平均化曲线
在ABAQUS有限元模拟过程中,需要输入纤维的应力-应变关系,利用式(6)—式(7)的转化关系将埋深为2 mm的拉拔模型转化为纤维的应力-应变关系。最终的应力应变关系如图5所示。

图5 换算后的纤维的应力-应变曲线
3 PVA-ECC受压试件的数值模拟
利用ABAQUS有限元软件建立考虑纤维与基体的二维细观模型,模拟彭晨星[14]的单轴压缩试验。抗压试件的尺寸为 ,纤维体积分数为2%,采用前文的二维线状纤维随机生成算法完成纤维在基体中的随机投放,其中纤维采用桁架单元建模、基体采用平面单元建模。纤维与基体之间采用ABAQUS中内置区域进行连接,既将纤维的所有节点与基体节点联系在一起,基体采用混凝土塑性损伤本构,纤维与基体之间的粘结滑移本构前文已详细介绍。同时如图6所示抗压试件的底边约束住水平、竖直、转动三个方向的约束,抗压试件的顶部采用位移加载,同时为了加快收敛,采用平滑分析步进行加载,加载位移为1.5 mm。纤维的网格尺寸为0.6 mm, 纤维单元的数量为4 551,基体的网格尺寸为1 mm,采用四边形单元划分网格,单元的数量为5 041。

图6 抗压模型的纤维分布及加载
如图7和图8所示,有限元模拟所得的荷载位移曲线以及应力应变曲线可以看到峰值荷载以及抗压强度分别为141.51 kN、38.22 MPa,峰值荷载对应的位移以及抗压强度对应的应变分别为0.235 mm、0.0033。其中抗压强度比文献中的试验数据高了6.42 MPa,可能是因为将模型简化为二维与实际结构存在一定的差距。同时,掺量为2%的PVA-ECC的抗压强度比PVA-ECC基体的抗压强度降低了1.58 MPa,可以看出纤维的加入对PVA-ECC抗压强度的影响较小。而PVA-ECC的峰值应变为0.0033,与普通砂浆的峰值应变差别不大,与试验中的峰值应变0.004也较为接近。同时,本文得出的荷载-位移曲线在下降段还能继续承受一定的荷载,与试验[15]得出的规律一致。因此总体来说,本文的模型具有一定的可行性。
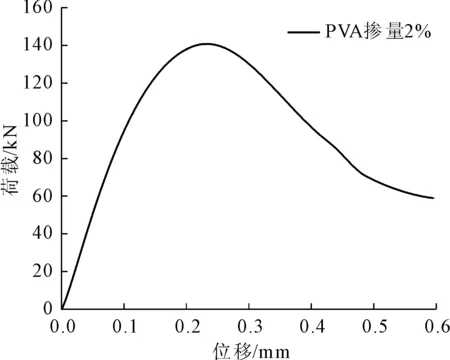
图7 ECC受压荷载-位移曲线

图8 ECC受压应力-应变曲线
图9分别给出了PVA-ECC抗压试件压缩位移为0.100 mm、0.235 mm、0.400 mm、0.600 mm时的受压损伤云图。可以看到在达到峰值荷载之前,ECC抗压试件的内部45度方向上出现明显的损伤,随着荷载的不断增加,内部出现的裂纹不断扩展,并逐渐连通。在达到峰值荷载时,出现了X形损伤,内部裂缝已经完全连通,其中两条对角线的交点处的损伤最为严重。随着荷载的继续增加,由于已经形成的连通裂缝之间有纤维的存在,纤维的桥接作用使得ECC抗压试件还可以继续承受较大的荷载,但此时ECC抗压试件的内部损伤已经较为严重,X形裂缝更加明显。随着荷载的进一步的增加,裂缝的宽度不断的扩大,裂缝之间的纤维逐渐被拔断或者拔出,ECC抗压试件两侧的部分基体逐渐脱落,ECC抗压试件彻底丧失承载力。图9还给出了纤维在ECC抗压试件丧失承载力时的应力云图,从图中可以看到基体对角线方向上的纤维受力较大。
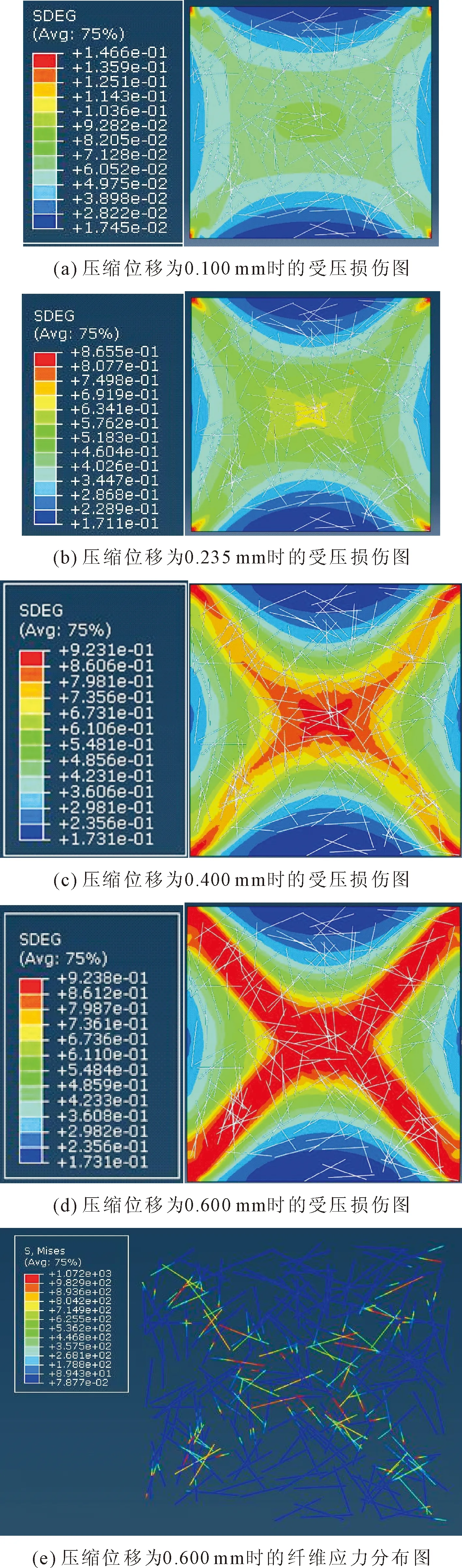
图9 纤维掺量为2%的PVA-ECC受压试件的破坏过程
4 PVA-ECC受拉试件的数值模拟
本节模拟了彭晨星[14]的单轴拉伸试验,利用ABAQUS有限元软件建立考虑纤维与基体的二维细观模型。单轴拉伸试验采取哑铃型试件,利用对称布置在试件中央两侧的夹式引伸计测量100 mm标距长度范围内的变形,如图10所示。模拟过程中抗拉试件的尺寸取哑铃型试件的标距段50 mm×150 mm,纤维体积分数为2%,基体本构以及纤维与基体之间的粘结滑移本构与前文受压模型一致。
如图11所示,抗拉试件的底边约束住水平、竖直、转动三个方向的约束,抗压试件的顶部采用位移加载,并选用顶部的中点建立参考点RP-1,利用ABAQUS中的耦合功能,将顶部表面耦合到参考点RP-1,提取RP-1的位移与反力荷载数据得到单轴受拉试验的荷载位移曲线,在RP-1上进行位移加载,同时为了加快收敛,采用平滑分析步进行加载,加载位移为1.5 mm。纤维的网格尺寸为0.6 mm, 纤维单元的数量为7 241,基体的网格尺寸为1 mm,采用四边形单元划分网格,单元的数量为7 500。
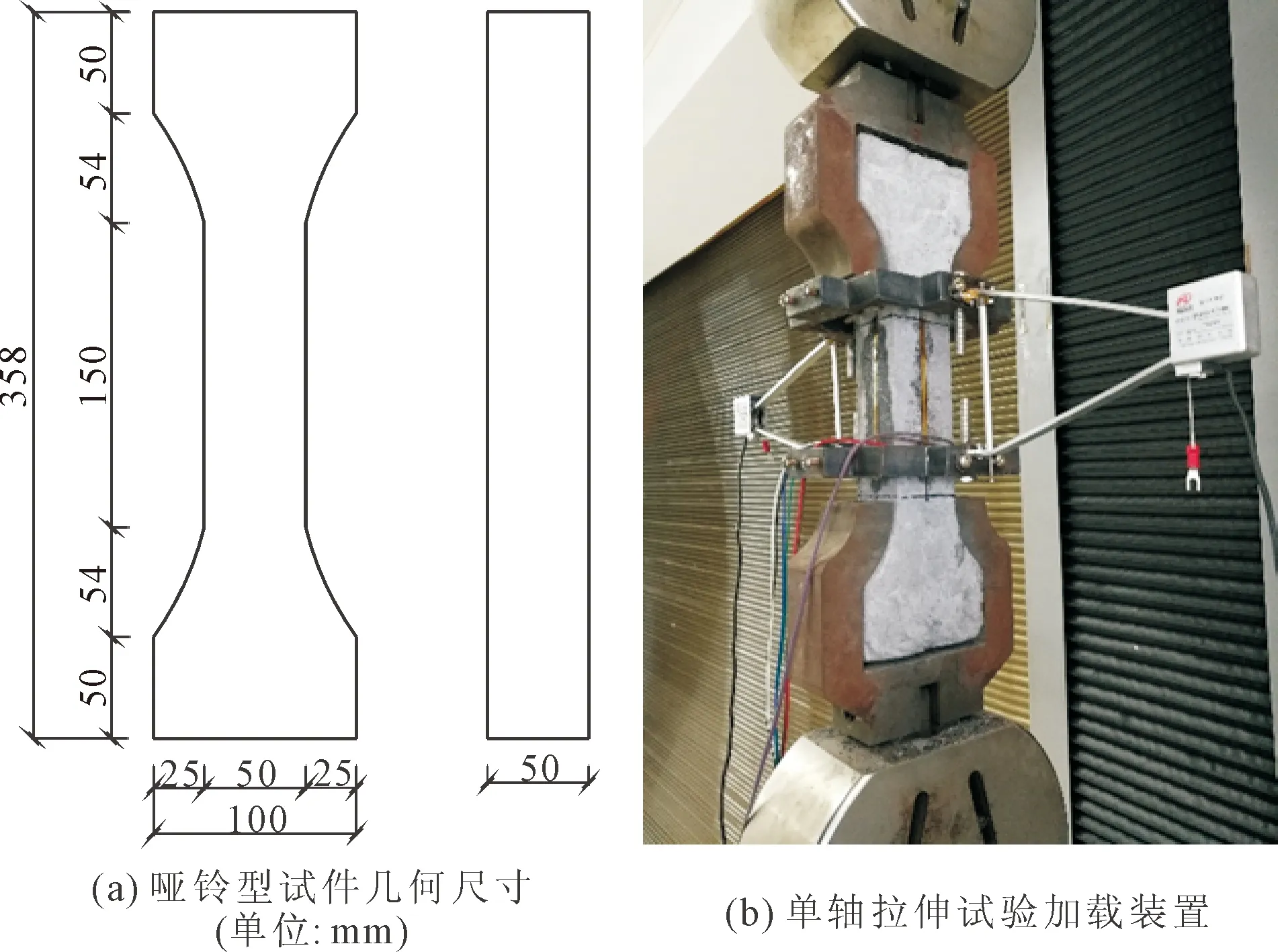
图10 单轴拉伸试验

图11 抗拉模型的加载方式
图12为两个细观模型得出的应力-应变曲线,并给出了试验得出的应力-应变曲线,可以看出模拟得出的应力-应变曲线与试验结果的吻合度较好,同时两条模拟曲线也都出现了屈服平台,并且吻合度也较好。表4给出了两条模拟曲线以及试验曲线的初裂应力、初裂应变、极限应力、极限应变的数值,从表中可以看到,模拟结果和试验结果的初裂应力分别为3.44 MPa和3.57 MPa,初裂应变分别为0.039%和0.035%,极限应力分别为3.74 MPa和4.42 MPa,极限应变分别为1.92%和2.22%。模拟结果的极限应力和初裂应力都比试验结果小,初裂阶段模拟结果和试验结果的曲线吻合较好,但进入屈服阶段后,应力的模拟结果比试验结果要小,同时模拟所得的应力-应变曲线更早的进入下降段,极限应变较试验结果偏低。但总的来说,两条模拟曲线都具有应变硬化平台,能够继续有效的承载,本文细观有限元可以有效的模拟PVA-ECC试件在单轴拉伸荷载作用下的应力-应变关系,既本文的细观模型具有一定的可行性。
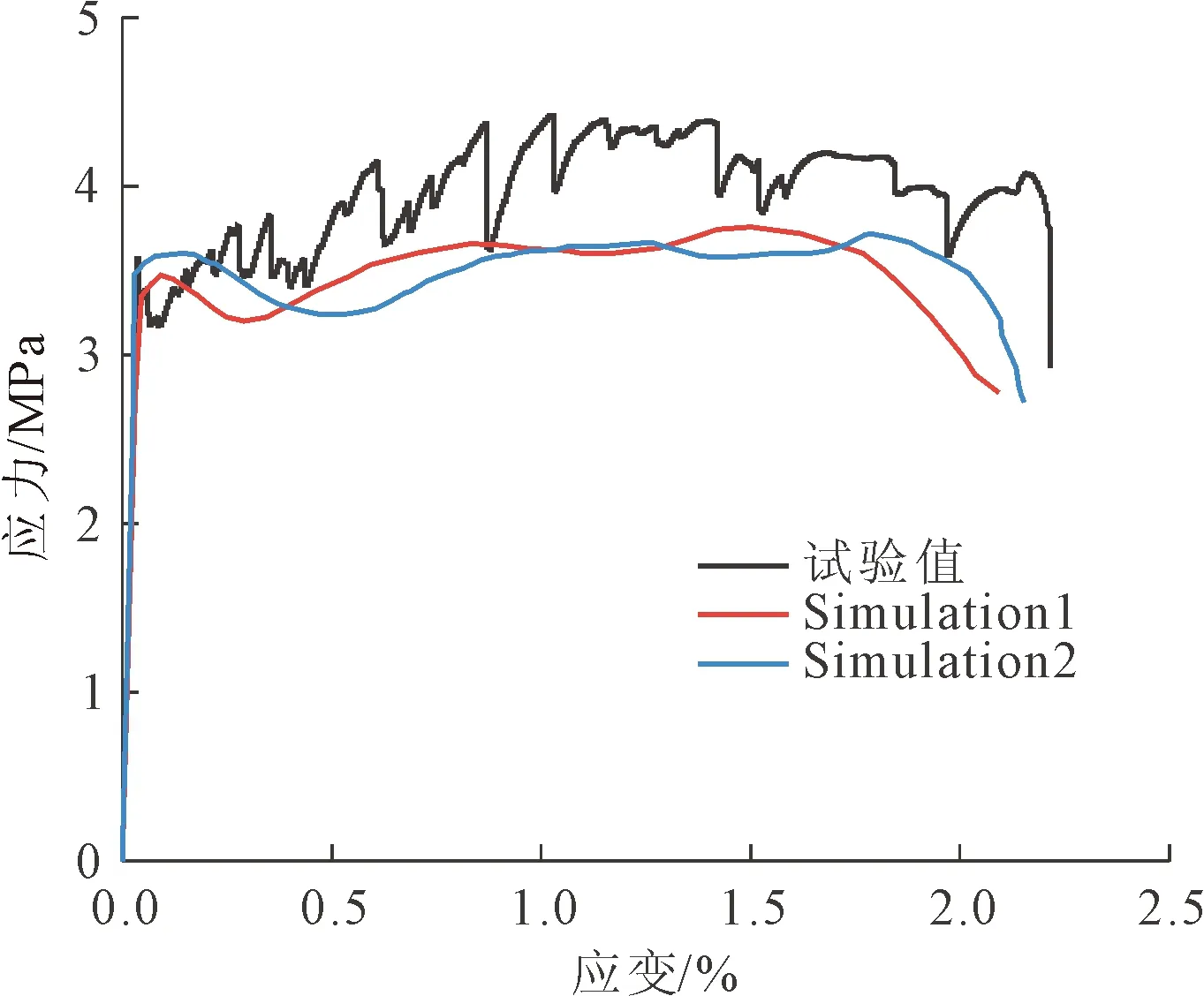
图12 PVA-ECC受拉试件的模拟曲线与试验对比
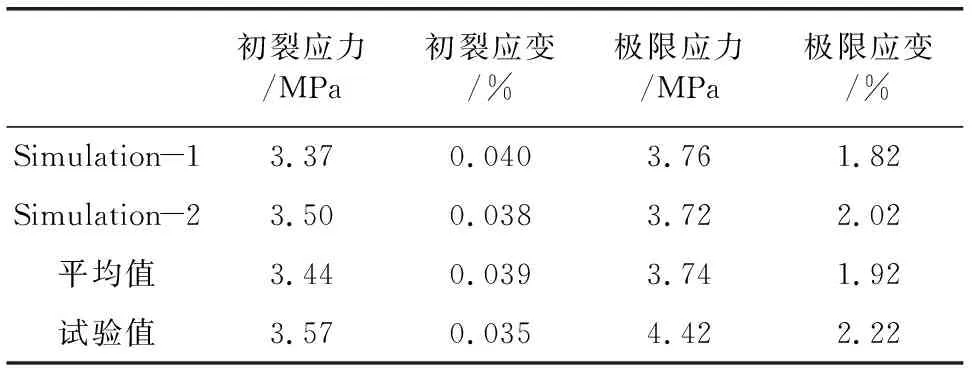
表4 PVA-ECC单轴受拉有限元模拟与试验结果对比
图13展示了Simulation1模拟的ECC受拉试件在整个拉伸过程中基体的损伤情况,图中分别展示了开裂阶段以及应变为0.5%、1%时的基体的受拉损伤情况,同时也给出了极限应变时基体的受拉损伤情况。从图13中可以清晰的看到ECC受拉试件在拉伸荷载作用下裂缝的开展过程,初裂阶段基体总体未受到损伤,当应变为0.5%试件的底部已经出现多条裂缝,当应变为1%时裂缝已经扩展到试件的中部,随着荷载的不断增大,当达到极限应变时,裂缝已经扩展至整个ECC试件,并且试件沿着其中一条最不利的裂缝发生断裂。因此,有限元模拟的ECC受拉试件在拉伸荷载作用下具有明显的应变硬化以及多缝开裂,本文的细观有限元模型具有一定的可行性。
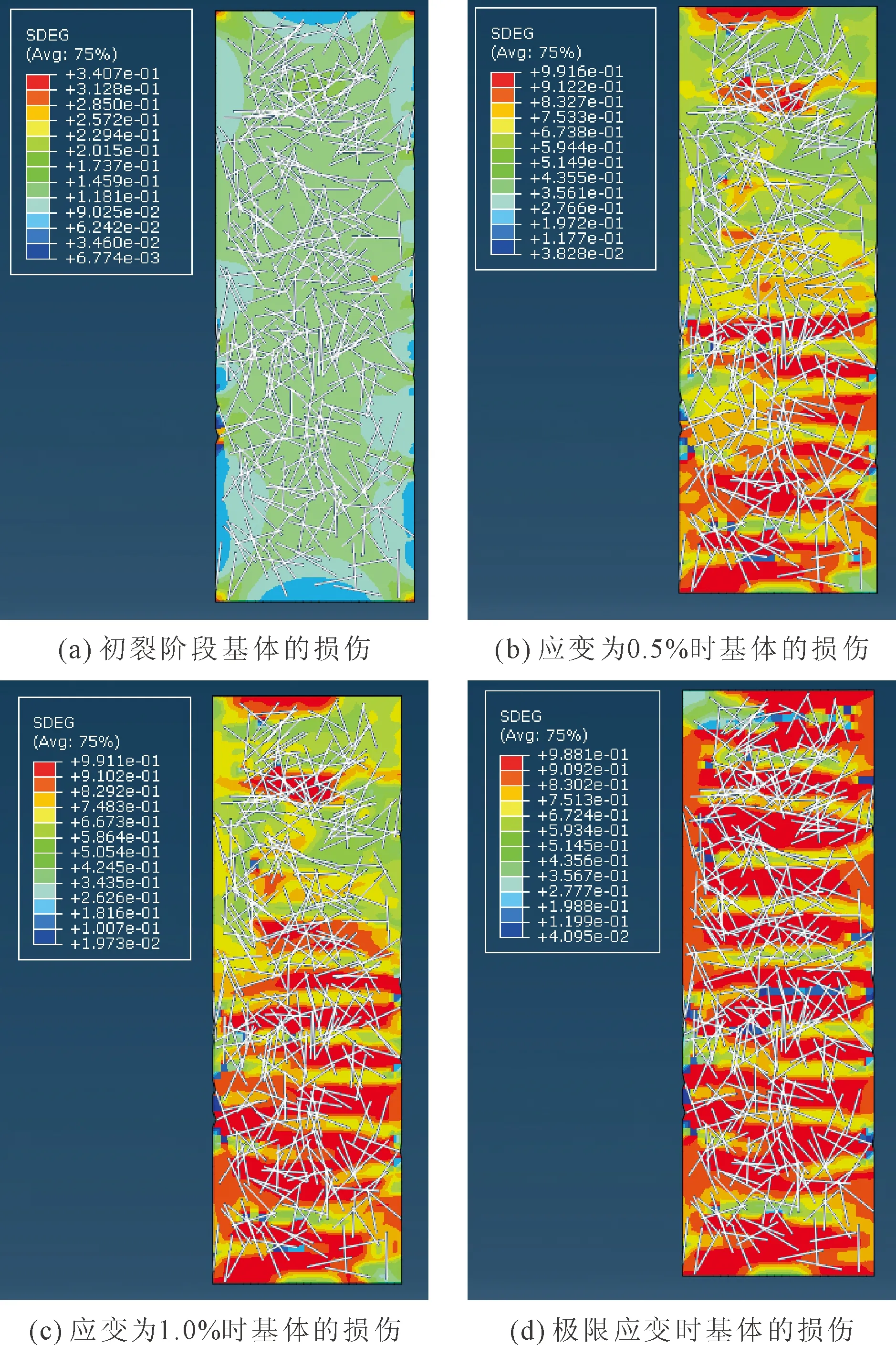
图13 纤维掺量为2%的PVA-ECC受拉试件件的破坏过程
5 结 论
建立了由基体、纤维组成的二维PVA-ECC细观有限元模型,并利用建立的细观有限元模型对在拉、压状态下的ECC试件进行数值模拟,得到以下结论:
(1) 利用细观有限元模型模拟了已有文献中的ECC受拉、受压试验,模拟得出应力应变曲线与试验结果吻合良好,验证了本文的细观有限元模型具有一定的可靠性,同时获得一些破坏规律。
(2) 研究了PVA-ECC材料破坏规律,受压模型在达到峰值荷载之前,ECC抗压试件的破坏与普通混凝土较为相似,内部45度方向上出现明显的损伤,随着荷载增加,内部裂纹扩展,并逐渐连通。在达到峰值荷载时,出现了X形损伤,内部裂缝已经完全连通,其中两条对角线的交点处的损伤最为严重。PVA纤维主要在峰值荷载之后发挥作用,使得ECC受压构件可以更进一步承受荷载。
(2) PVA-ECC受拉模型出现了多缝开裂的破坏形态,随着荷载的不断增大,裂缝逐渐扩展,直到裂缝扩展到整个试件,并且试件沿着其中一条最不利的裂缝发生断裂。

