基于多路延时对准的旋转惯导系统传递对准方法

田凯文，董壮壮，程广新，李 鼎，杨开勇，于旭东

基于多路延时对准的旋转惯导系统传递对准方法

田凯文，董壮壮，程广新，李 鼎，杨开勇，于旭东

（国防科技大学前沿交叉学科学院，长沙 410073）

针对惯性导航系统的传递对准信息品质受周期性振荡误差影响的问题，通过分析周期性振荡误差的产生机理，提出了一种基于多路延时对准的舒勒振荡误差抑制方法，将数据错开一定比例的舒勒周期进行对准，多路信号先后进入导航解算，之后进行数据融合，可以达到抑制舒勒周期振荡误差、提高传递对准信息品质的效果。经过静态、动态实验验证，该方法可以有效提高子惯导在传递对准过程中的惯性器件误差估计的精度与稳定度，可以使子惯导完成高精度的惯性器件误差估计。

传递对准；延时对准；惯性导航系统；舒勒振荡误差

0 引言

惯性导航系统简称惯导系统（inertial navigation system, INS）能够实现全天候、全自主、长航时的导航，是潜艇等舰船进行导航定位的关键系统[1-3]。惯导系统在工作过程中具有舒勒周期误差、傅科周期误差、地球周期误差3种周期性振荡误差，这些振荡误差会极大增加导航速度误差与位置误差，使惯导系统长航时的导航精度大大降低。尤其是对于旋转惯导系统，由于旋转调制已经将惯性器件误差和初始对准误差控制得较小[4-7]，因此周期性振荡误差在一定时间内占据影响导航精度的主要部分。

传递对准是子惯导导航信息动态地匹配主惯导导航信息的过程[8-10]。将带有周期性振荡误差的主惯导导航信息传给子惯导进行传递对准，其对准效果将大大降低。因此，提高主惯导传递信息品质，减小主惯导的周期性振荡误差，使其给子惯导提供更高精度的传递对准参量，具有重要的实际意义。

目前抑制舒勒周期振荡误差的方法主要有阻尼技术和组合导航技术[11-12]。阻尼技术分为外阻尼技术和内阻尼技术，外阻尼技术通过借助外速度来抑制舒勒周期振荡，内阻尼虽然可以在不借助外部信息的情况下抑制舒勒周期振荡，但是也仅适用于低机动状态，当载体处于高机动运行状态时，系统将产生动态误差，这反而会使惯导系统的导航精度降低，并且阻尼系统在无阻尼状态和阻尼状态切换时，产生的超调误差也会严重影响惯导系统的导航精度与导航信息的稳定性[13]。组合导航技术是融合惯导与其他导航系统的信息，信息进行互补，达到抑制周期性振荡误差的效果。采用组合导航技术虽然可以有效地抑制舒勒周期振荡误差，但是借助了其他外部信息，使惯导系统的自主性遭到破坏。因此，寻找一种既不改变惯导系统自主性又能有效抑制舒勒周期振荡误差的方法具有重要意义。

针对主、子惯导均为旋转调制惯导系统的情况，本文对基于多路延时对准的传递对准算法展开研究，旨在提高传递信息品质与传递对准精度。

1 惯导系统舒勒周期振荡误差分析

由于无阻尼惯导系统的动态误差特性和静态误差特性差别较小，且在静止条件下可以更好地体现惯导系统的误差特性，因此为了简化问题，可基于忽略垂向通道的静基座惯导系统误差方程进行分析。静基座惯导系统误差方程为：

式（1）的拉氏变换方程为

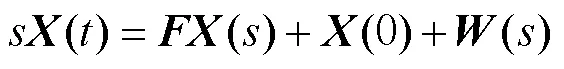
可求得式（2）的特征方程的特征根为：

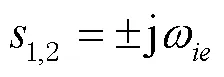
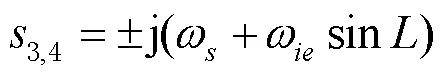
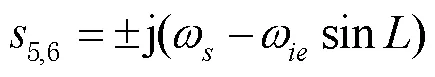
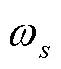
当惯导系统的器件误差和初始对准误差等其他误差量被调制为小量，上述的周期性振荡误差占据影响惯导系统精度的主要部分时，如若惯导系统具有标准的周期性振荡误差，采用多路延时对准的方法，将错开一定振荡周期后对准的多路数据进行数据融合，可以减小主惯导的周期性振荡误差[14]，将有效提升传递对准信息的品质。

2 基于多路延时对准的传递对准

2.1 多路延时对准方案设计

由于一般用于航海的高精度旋转惯导对准时间会达到十几小时，舒勒振荡周期与之相比较短，牺牲一定舒勒振荡周期的时间是完全可行的。傅科振荡与舒勒振荡耦合在一起，因此将舒勒振荡抑制后，傅科振荡自然也会受到抑制。地球振荡周期由于周期过长，在实际使用中牺牲一定地球振荡周期不具有可行性[15]。因此，以下均针对抑制舒勒振荡误差进行方案设计。

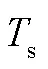
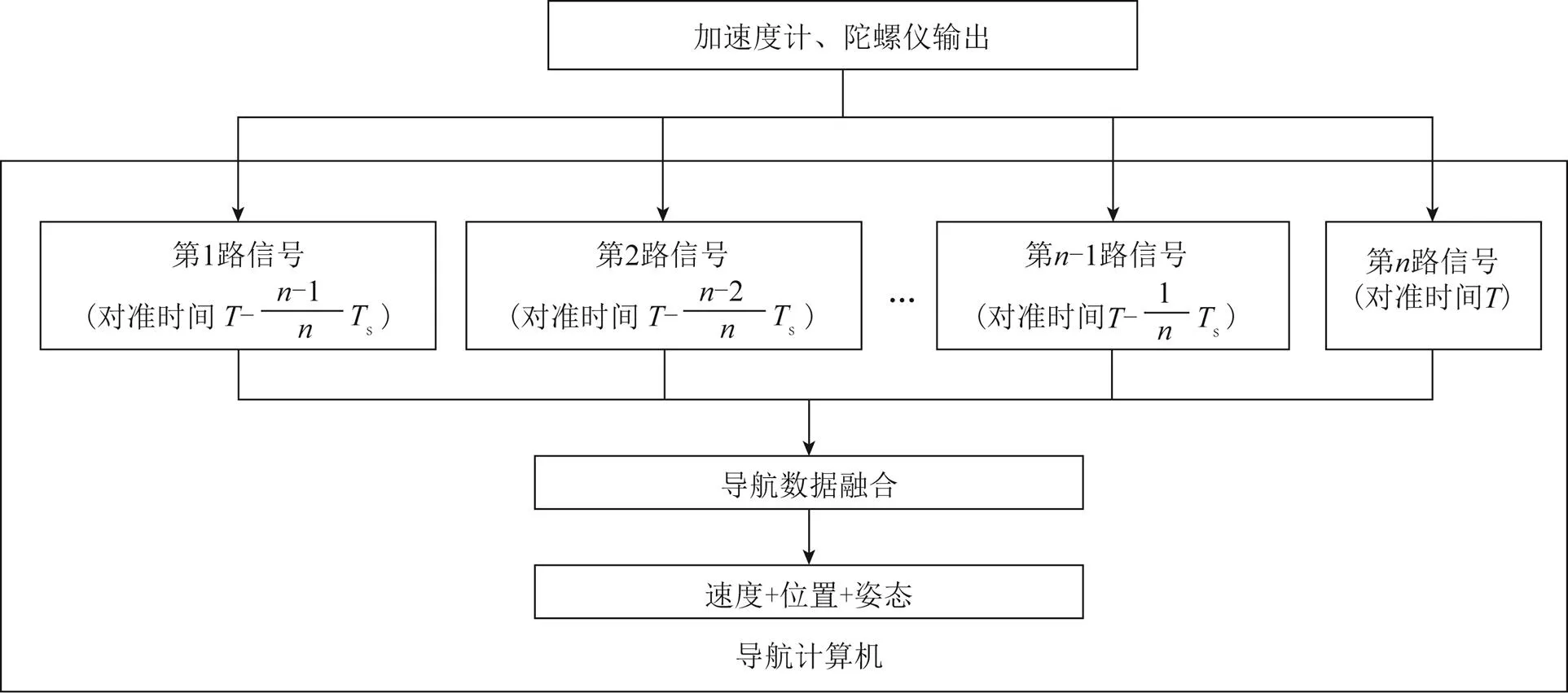
图1 多路延时对准方案设计

以2路延时对准为例，一路信号对准后正常时刻进入导航解算，另一路信号延时对准T/2，2路信号错开T/2进入导航解算。即假设原初始对准时长为10 h，2路同时开始对准，则信号1对准(10 h-T/2)后进入导航，信号2对准10 h后进入导航，以信号2进入导航的时刻记为系统进入导航。

信号1和信号2的舒勒振荡误差的方程为：

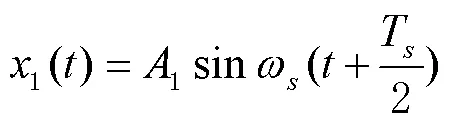
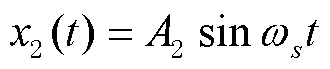
将2路信号融合后，输出为

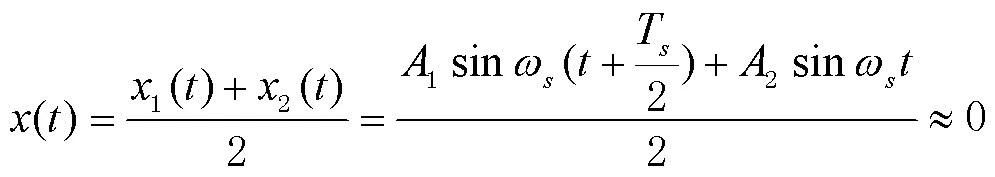
因为信号1和信号2是由同一陀螺加表数据经对准和导航解算得到的，2种信号的幅值、大小接近，因此由式（8）可知，对信号1和信号2取均值，可以很好地抑制舒勒振荡误差。图2给出了2路延时对准的舒勒振荡误差抑制示意图。

图2 2路延时对准的舒勒振荡误差抑制示意图

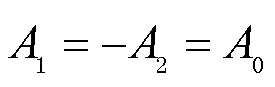
理论上延时对准的信号路数越多，最差情况下对舒勒振荡的抑制效果就越好，系统整体对舒勒振荡误差的抑制效果就越稳定。但是由于多路信号在导航计算机内是并行运算，信号路数过多会导致运算量过大，对惯导系统的导航芯片的运算能力有很高的要求。因此考虑到当前导航计算机的运算能力，在实验中采用4路延时对准的方式。

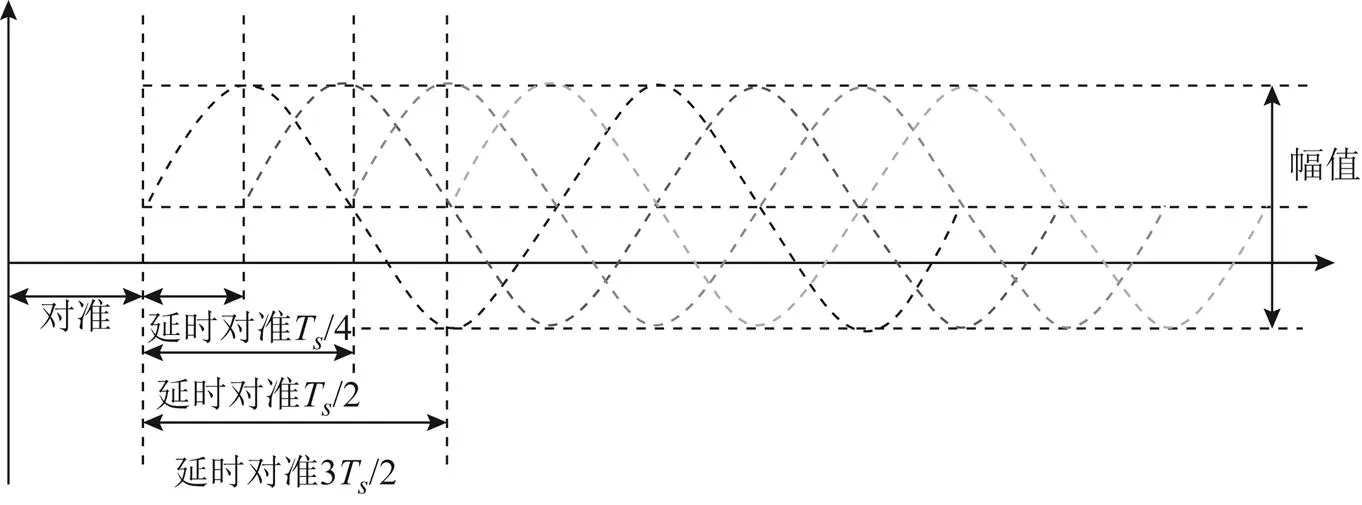
图3 4路延时对准的舒勒振荡误差抑制示意图

2.2 速度匹配传递对准滤波模型

针对主、子惯导均为旋转惯导系统的情况，选取速度匹配传递对准，由于主、子惯导的精度相当，因此主惯导的输出速度误差就成为制约传递对准效果的重要因素[16]。

2.2.1 速度匹配传递对准状态方程

选取状态量为

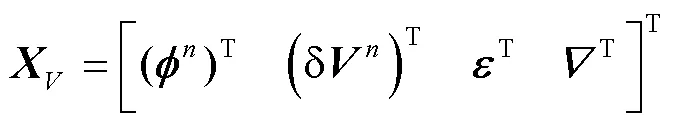
传递对准系统误差模型为

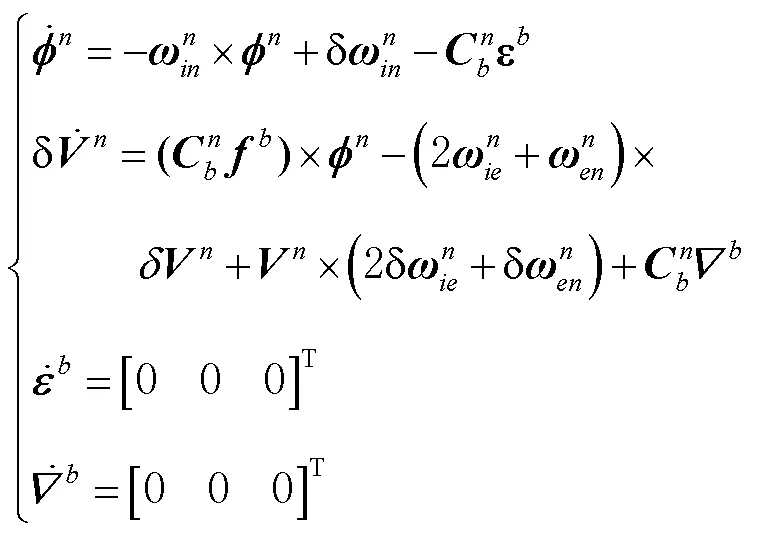
根据式（10），速度匹配传递对准状态方程可写成矩阵形式：

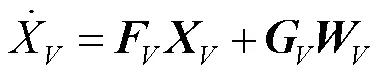
2.2.2 速度匹配传递对准量测方程

速度匹配传递对准量测方程为

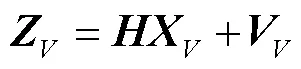
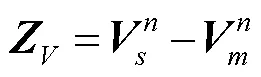
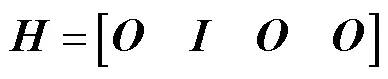
3 实验与结果分析

3.1 静态实验

图4 主惯导4路延时对准静态导航误差结果

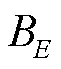
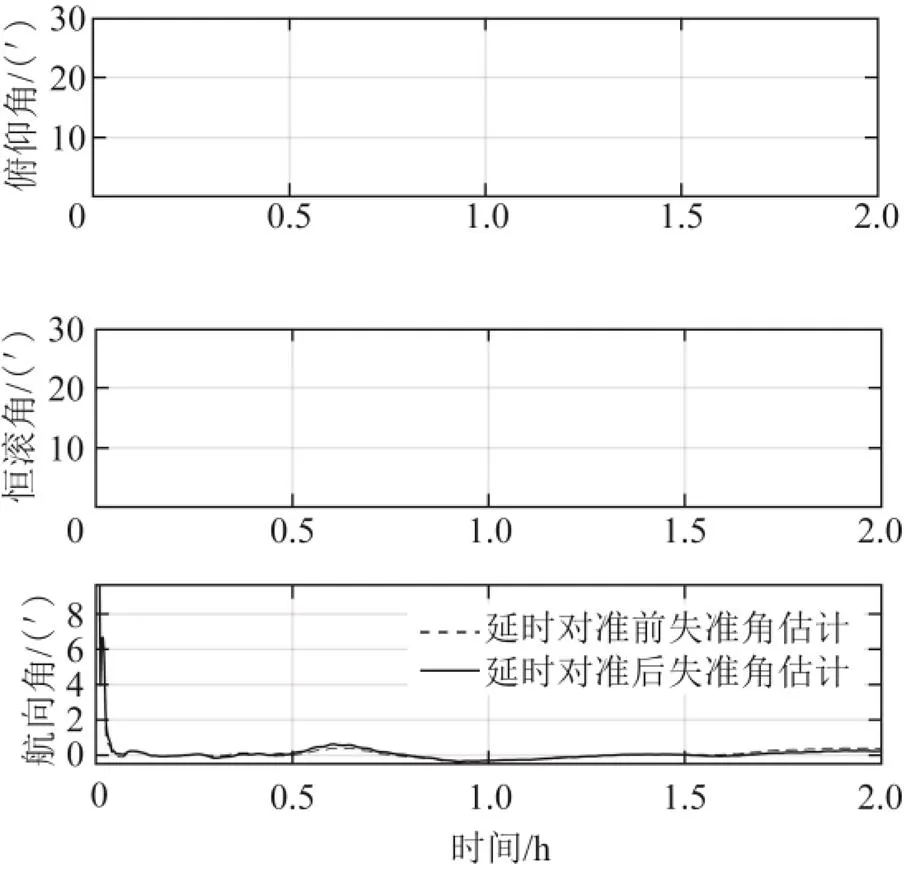
图5 子惯导传递对准失准角估计误差

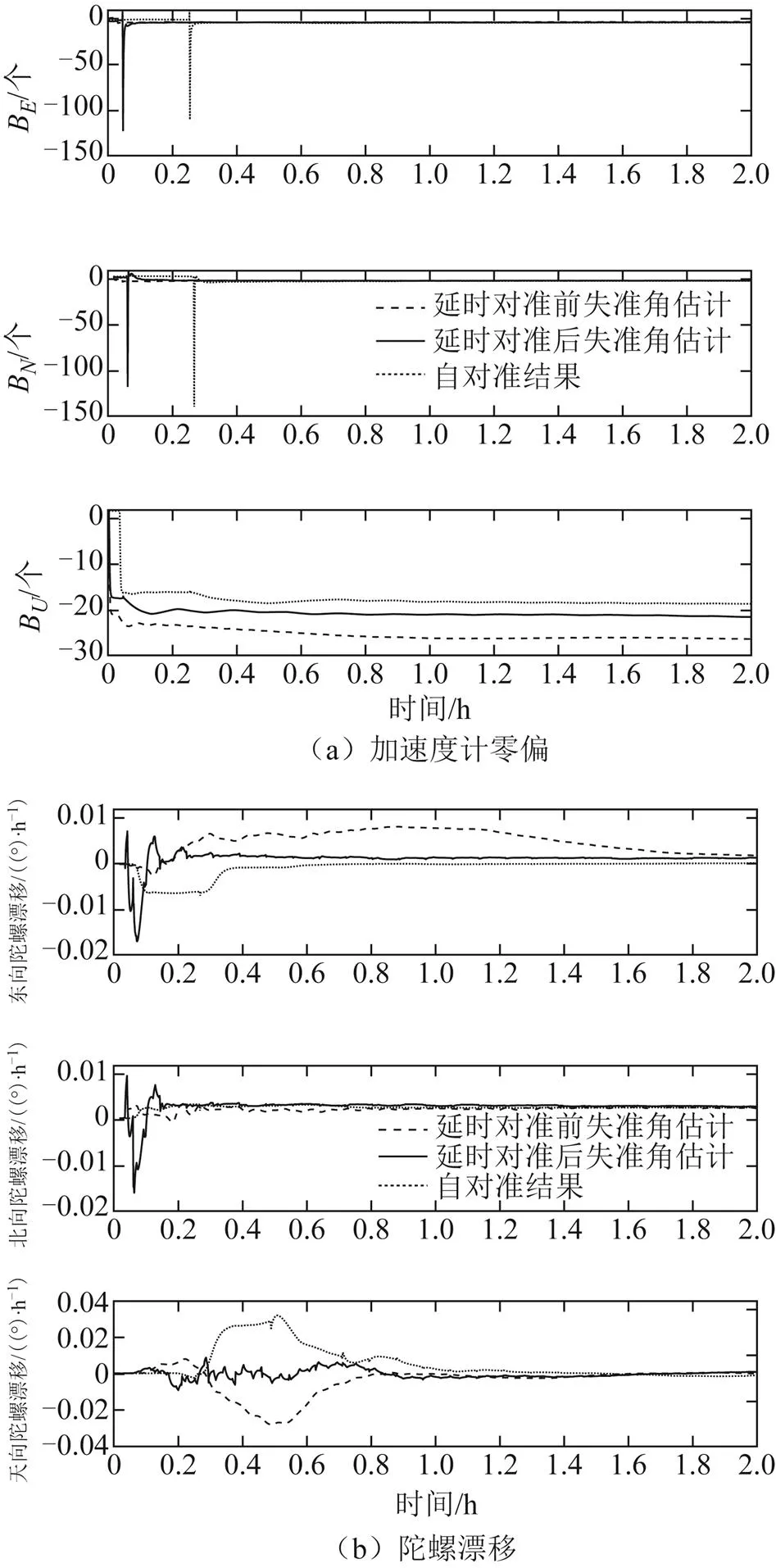
图6 子惯导传递对准惯性器件常值误差估计

3.2 动态实验

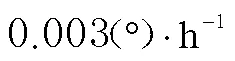
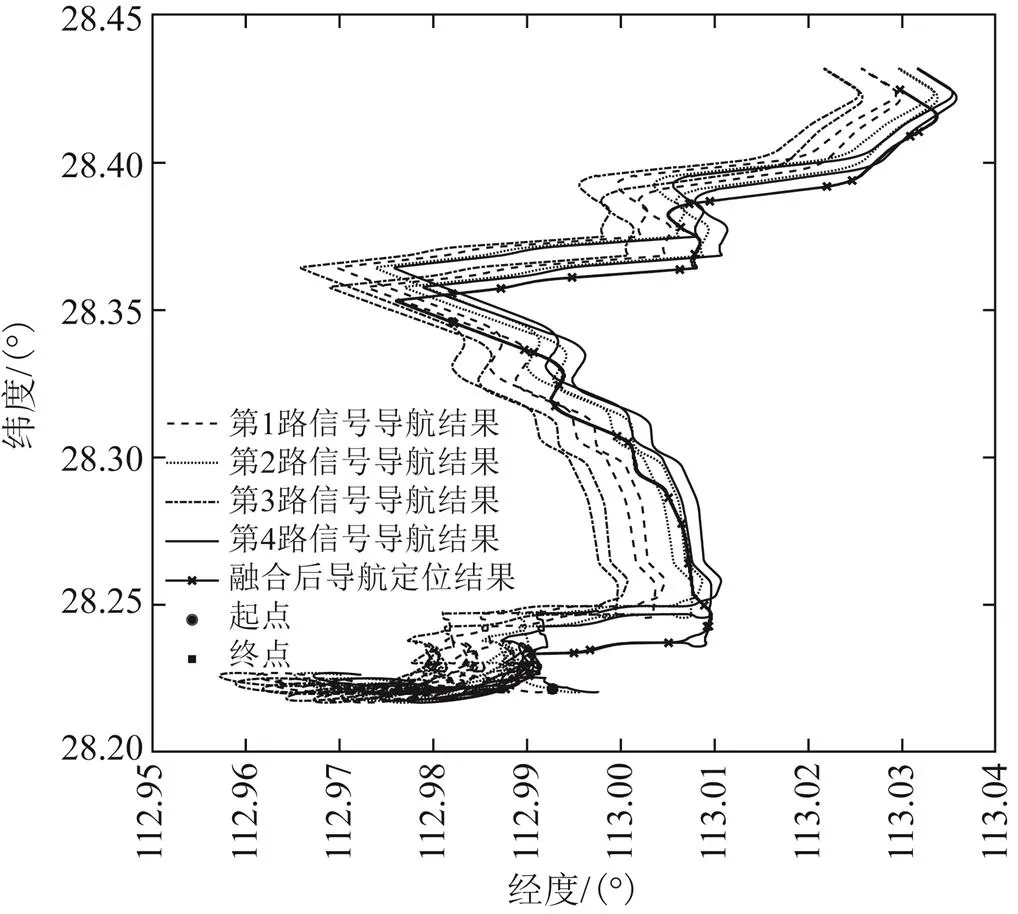
图7 动态跑车实验4路延时对准导航结果

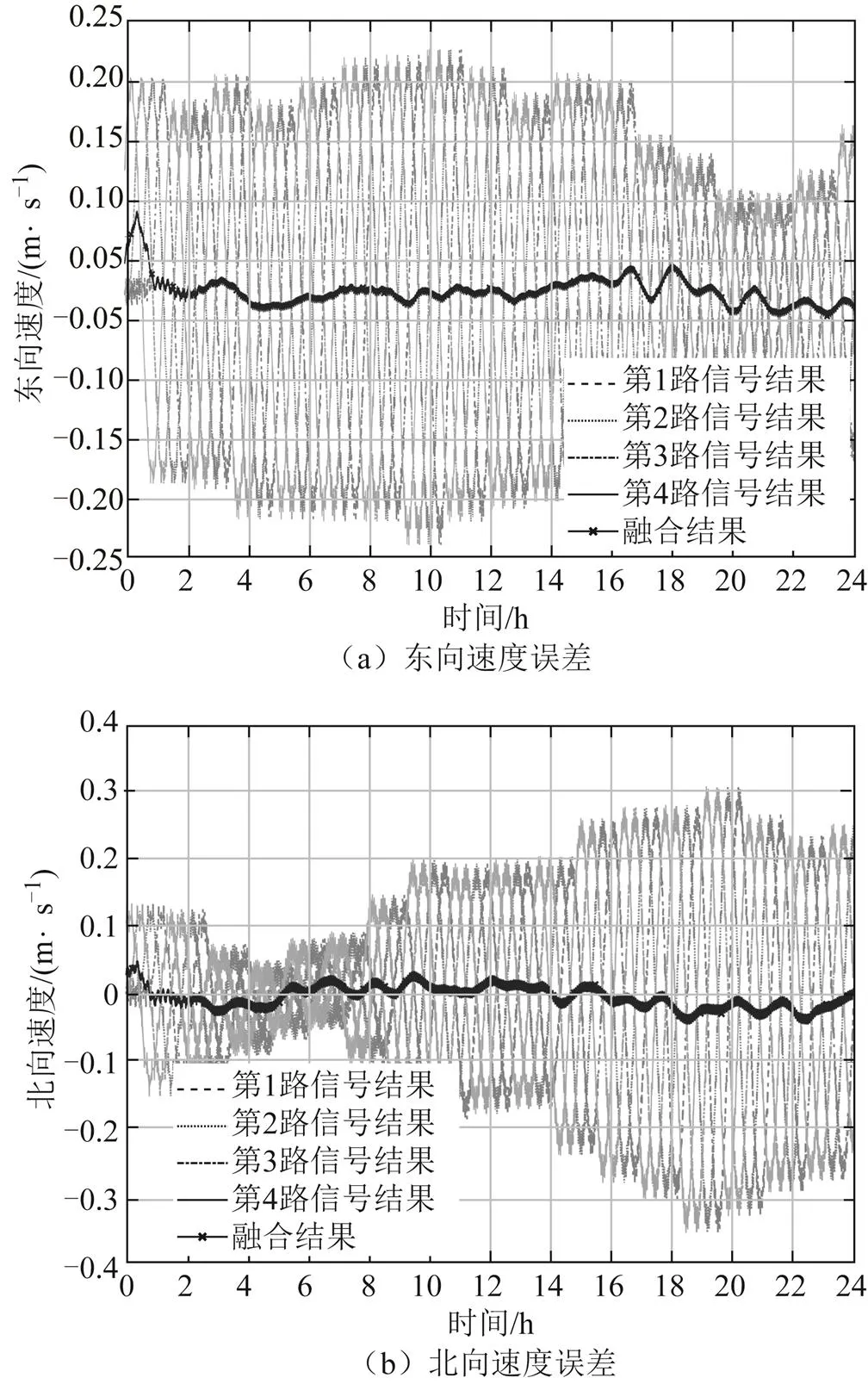
主惯导在动态下对子惯导进行2 h传递对准，图9为子惯导传递对准失准角估计误差图，图10为子惯导惯性器件常值误差估计图。使用延时对准算法后子惯导天向失准角收敛更快，子惯导的天向加表零偏估计误差减小了约78.4%，东向陀螺。漂移的振荡幅度减小了约17.6%，北向陀螺漂移估计误差减小了约41%。

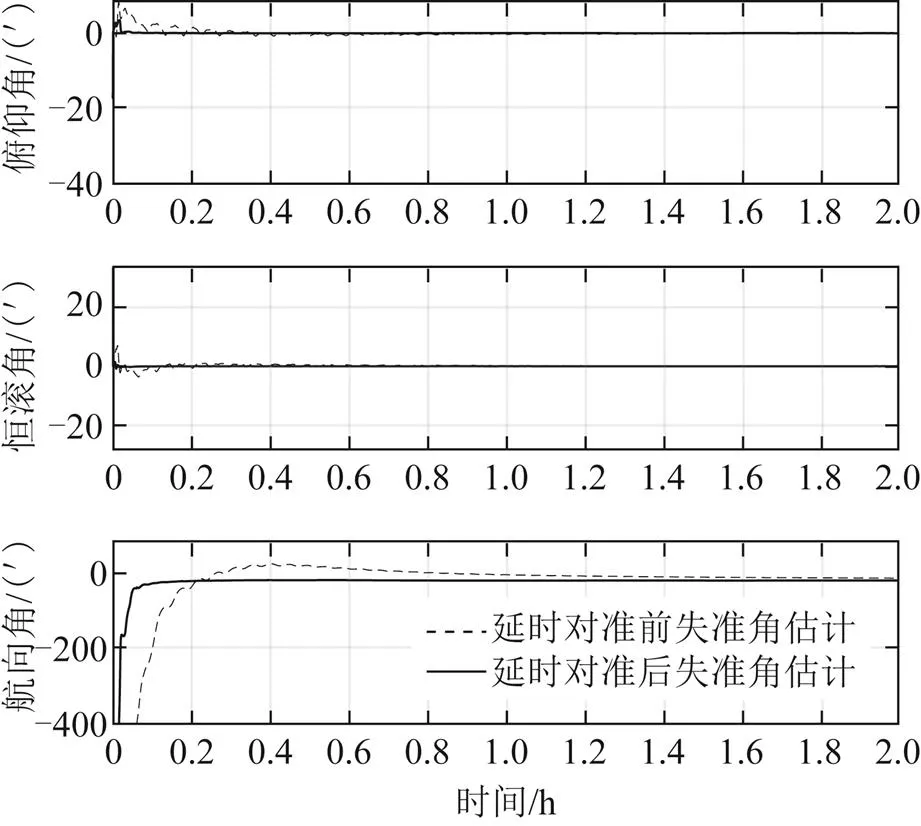
图9 子惯导传递对准失准角估计误差

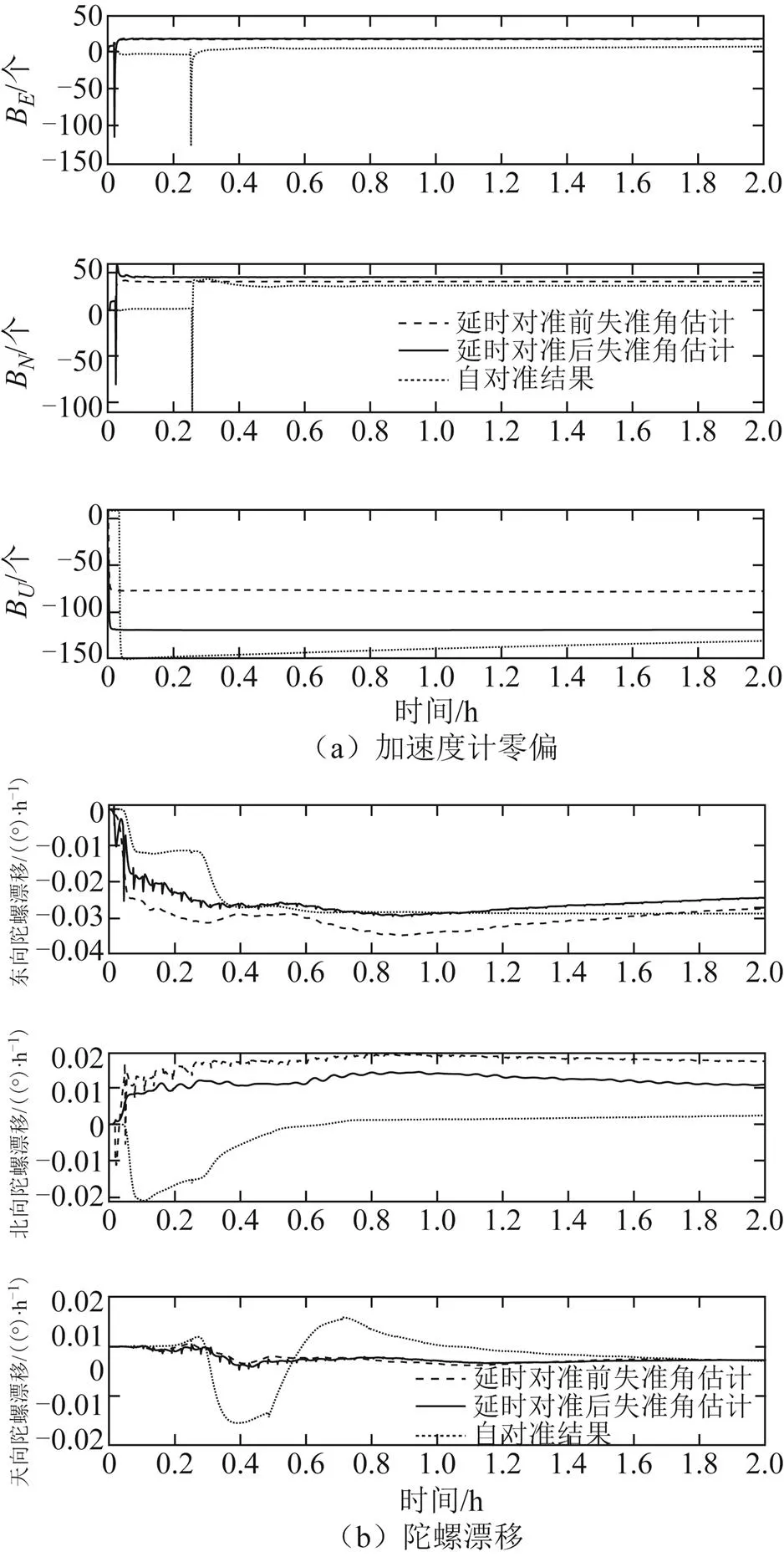
图10 子惯导惯性器件常值误差估计

4 结束语

周期性振荡误差的存在大大降低了惯导系统的传递对准信息品质，进而影响子惯导的传递对准精度。文中提出了一种基于多路延时对准的舒勒振荡误差抑制方法，通过将多路数据错开一定比例的舒勒周期进行初始对准，之后将各路的导航结果融合，抑制了主惯导的舒勒周期振荡误差，提高了传递对准信息品质，使得子惯导在传递对准中能够对其惯性器件误差达到高精度和稳定的估计，可满足高精度、长航时导航与定位的需求。

[1] 薛连莉, 翟峻仪, 葛悦涛. 2020年国外惯性技术发展与回顾[J]. 导航定位与授时, 2021, 8(3): 59-67.

[2] 姬晓琴, 陈文辉, 杨业. 旋转惯导的发展及应用[J]. 航天控制, 2019, 37(1): 27-33.

[3] 冯培德. 惯导产品系统技术的提升大有可为[J]. 导航与控制, 2020, 19(增刊1): 15-17.

[4] HAN H, WANG L, WANG M. An online gyro scale factor error calibration method for laser RINS[J]. IEEE Sensors Journal. 2021, 21(13): 15291-15298.

[5] CAI Q, YANG G, SONG N, et al. Analysis and calibration of the gyro bias caused by geomagnetic field in a dual-axis rotational inertial navigation system[J]. Measurement Science & Technology, 2016, 27(10): 105001.

[6] LIU Z, WANG L, LI K, et al. Analysis and improvement of attitude output accuracy in tri-axis rotational inertial navigation system[J]. IEEE Sensors Journal. 2020, 20(11): 6091-6100.

[7] SONG T, LI K, WANG L, et al. A rapid and high-precision initial alignment scheme for dual-axis rotational inertial navigation system[J]. Microsystem Technologies, 2017, 23(12): 5515-5525.

[8] 史荣宗, 马晨, 郭正玉. 速度匹配算法在传递对准中的应用分析[J]. 系统工程与电子技术, 2020, 42(10): 2328-2333.

[9] 符彦，王剑辉，韩菲. 地固坐标系下捷联惯导系统初始精对准[J]. 导航定位学报, 2019, 7(4): 50-55.

[10] 王文君，柴艳菊. 不同精度INS精度分析与评估方法[J]. 导航定位学报, 2020, 8(3): 87-91.

[11] 王振华. 传递对准中主惯导误差分析及处理方法研究[D]. 哈尔滨:哈尔滨工程大学, 2020.

[12] 汪湛清, 房建成, 汪顺亭, 等. 消除舒拉振荡误差的理论与实践[J]. 中国惯性技术学报, 2012, 20(4): 395-399.

[13] 刘灿, 龙兴武, 魏国, 等. 捷联惯导系统内水平阻尼网络及算法研究[J]. 红外与激光工程, 2014, 43(8): 2637-2643.

[14] 赵琳, 李久顺, 程建华, 等. 基于延时对准船用捷联惯导舒勒振荡抑制方法[J]. 系统工程与电子技术, 2016, 38(10): 2375-2380.

[15] 高春峰. 二频机抖激光陀螺在冗余配置及混合配置状态下的若干关键技术研究[D]. 长沙：国防科技大学, 2018.

[16] 刘为任, 唐艳, 朱蕾, 等. 主惯导旋转调制对传递对准性能的影响[J]. 中国惯性技术学报, 2011, 19(1): 16-20.

Transfer alignment of rotational INS based on multi-channel delayed alignment

TIAN Kaiwen, DONG Zhuangzhuang, CHENG Guangxin, LI Ding, YANG Kaiyong, YU Xudong

（College of Advanced Interdisciplinary Studies, National University of Defense Technology, Changsha 410073, China）

In order to solve the problem that the transfer alignment information quality of inertial navigation system (INS) is affected by periodic oscillation error, by analyzing the mechanism of periodic oscillation error, a Schuler oscillation error suppression method based on multi-channel delayed alignment is proposed. The data staggered a certain proportion of Schuler period are aligned respectively, and the multi-channel signals are successively entered into the navigation solution, followed by data fusion. It can restrain the Schuler oscillation error and improve the information quality of transfer alignment. Through static and dynamic experiments, it can be found that this method can effectively improve the accuracy and stability of inertial elements’ error estimation of slave INS in the process of transfer alignment, and enable slave INS to complete high-precision inertial elements’ error estimation.

transfer alignment; delayed alignment; inertial navigation system; Schuler oscillation error

TN249

A

2095-4999(2022)06-0136-08

田凯文，董壮壮，程广新，等. 基于多路延时对准的旋转惯导系统传递对准方法[J]. 导航定位学报, 2022, 10(6): 136-143.（TIAN Kaiwen, DONG Zhuangzhuang, CHENG Guangxin, et al. Transfer alignment of rotational INS based on multi-channel delayed alignment[J]. Journal of Navigation and Positioning, 2022, 10(6): 136-143.）

10.16547/j.cnki.10-1096.20220618.

2022-07-11

国家自然科学基金项目（62173335）；湖南省科技重大专项（2019GK1012）。

田凯文（1997—），男，陕西宝鸡人，硕士研究生，研究方向为激光陀螺及惯性导航系统。

于旭东（1982—），男，吉林长春人，博士，副研究员，研究方向为激光陀螺及惯性导航系统。