未知系统动态估计器在永磁同步电机控制中的应用

王立刚

（宜宾学院智能制造学部，四川宜宾 644007）

随着永磁体材料成本的下降，采用永磁材料的各类电机，尤其是永磁同步电机（Permanent Magnet Synchronous Motor,PMSM）已在工业系统中被广泛使用.永磁同步电机是一个强耦合、多变量、高阶非线性时变系统.在实际应用中，控制系统中的不确定性干扰会降低运动控制性能，按照文献[1]所列，控制系统中不确定性干扰分为内部扰动和外部扰动.内部干扰有电机参数变化，建模误差，反电势扰动等；外部干扰有摩擦力，负载，传感器误差等.

电机控制的闭环负反馈系统的调节器大部分是采用经典线性PID控制算法，但其在抗扰能力方面存在局限性.随着现代控制理论和智能控制等发展和芯片计算速度的提升，一些先进复杂控制策略也被应用于电机控制系统中[2-3]，如：滑模变结构控制[4-7]、非线性PID[8]、反演控制（Backstepping Control）[9]、自适应控制[10-11]、鲁棒控制[12]、智能控制[13-15]等.虽然以上方法能抑制系统的扰动，但都仅依赖反馈控制的机理，动态响应过程依然相对较慢，且对于时变干扰抑制效果并不理想.而以模糊控制、神经网络控制等为代表的智能控制在实际应用中，对处理器计算性能要求较高，故实际应用仍不够成熟.

鉴于上述方法对时变干扰抑制的局限，可考虑通过前馈控制补偿干扰的作用，即从干扰观测和前馈补偿组合策略提高系统抗扰动性能.从这个角度出发，Ohnishi提出一种干扰观测器（Disturbance Observer,DOB）对直流电机系统中扰动进行观测估计，并将其进行前馈补偿抵消干扰的影响[16].此后，顺着这一思路，众多基于DOB的控制方法被用到了实际系统当中[17-20].在近十年中，国内外学者还研究了多种观测扰动的方法，并将之应用到永磁电机运动控制领域，如：扩展状态观测器（Extended State Observer,ESO）[21-22]，非线性干扰观测器（Nonlinear Disturbance Observer,NDO）[23]和滑模型观测器[24]、自适应观测器[25]、Kalman滤波器[26]、Luenberger观测器[27]、模糊观测器[28]等.这些基于干扰观测器的方法大多依赖于控制对象的精确模型，因此被控对象建模与模型参数辨识一直是其关键问题与研究热点.

基于DOB的控制可以补偿非参数化不确定性，并具有简单的结构.在一般的非线性DOB设计中，观测器具有与原始系统相似的结构，且要设置若干个参数[2]，较为复杂.文献[3]则提出了一个简单且有效的未知系统动态观测器来解决系统未知动态估计问题，且其收敛性和鲁棒性也得到了严格的分析.本文提出一种新的未知系统动态估计器（Unknown System Dynamics Estimator,USDE），只需设置一个常数且结构简单，而其收敛速度和稳态响应则和其他常用观测器相同；分别应用在永磁同步电机控制系统的速度环和电流环上，按照两步设计方法[1]设计了基于USDE的抗干扰速度、电流控制器，实现了两个环路中的干扰抑制；最后通过仿真对比验证了该方法的有效性，提高了PMSM速度控制系统的精度.

1 PMSM数学模型及经典矢量控制

PMSM的数学模型通过坐标变换进行化简，得到dq坐标下的PMSM数学模型[29-30]：

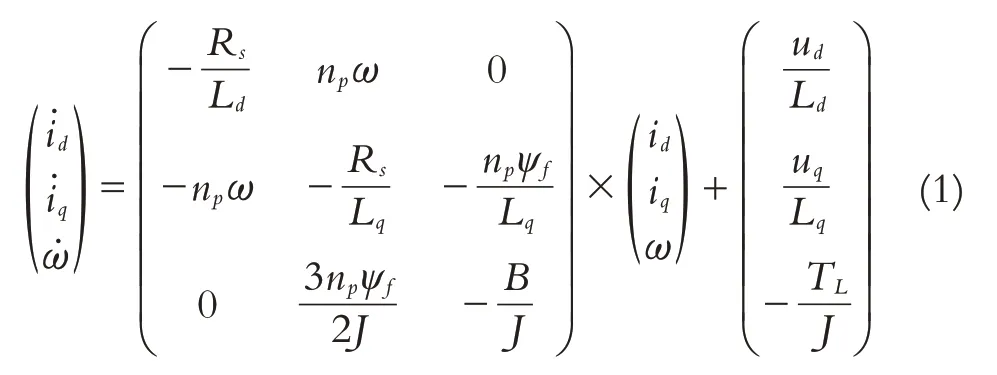
式中：ω为电机转子角速度，np是电机极对数，ψf为已知电机永磁体磁链，TL为负载转矩，Rs为定子电阻，id,iq为d轴和q轴的定子电流，ud,uq为d轴和q轴的定子电压，Ld,Lq为定子电感，Ld=Lq；B为粘性摩擦系数，J为转子转动惯量.图1为目前最常见的PMSM矢量控制系统原理图.

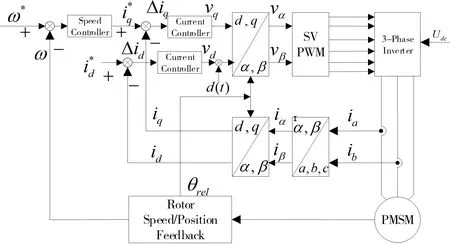
图1 PMSM矢量控制系统结构框图

整个控制系统有3个控制器，分别为速度控制 器、q轴电流控制器和d轴电流控制器，这里主要基于USDE设计速度控制器和d，q轴电流控制器来代替常规的PID控制器，以提高控制系统抗干扰能力.根据文献[30][31]两步控制器设计法，本文将设计基于USDE的PMSM控制系统.

2 控制器设计

2.1 基于未知系统动态估计器的速度控制器设计

在速度环中主要的干扰有电机参数变化、不确定性，摩擦力、电流环中的跟踪误差、负载转矩变化等.为了提高PMSM系统的性能，设计基于USDE速度环控制器.

按照i★d=0设计控制策略，且考虑转矩阻尼，Ld=Lq，PMSM系统电磁转矩方程代入运动平衡方程得PMSM系统的转速方程为

2.1.1 未知系统动态估计器设计

为补偿未知动态对控制系统的影响，设计未知动态估计器.定义ω，i★q的滤波后的变量为ωf，i★qf，则

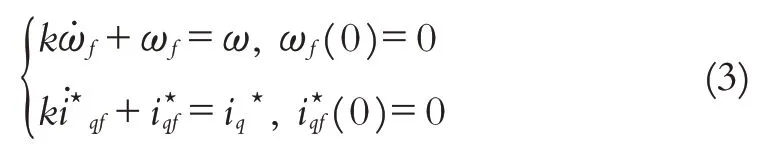
其中k＞0为滤波器参数.

根据不变流形[33]的分析，有如下结论：

定理1[3]考虑系统(2)和滤波操作(3)，则

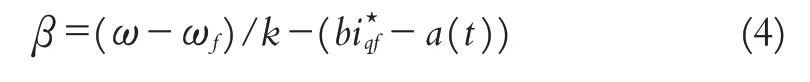
最终有界，且对任意有限常数k＞0，有

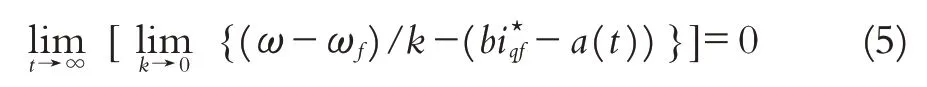
证明：证明可以参考文献[3].

上述不变流形给出了一个从滤波变量ωf，i★qf到未知动力学a(t)的映射.因此，它可以在不知道ω˙信息情况下，设计a(t)的估计器为

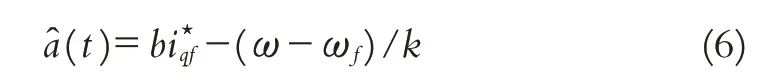
显然，设计者只需选择滤波常数k＞0.

本文提出的估计器的收敛性可以归纳为定理2.

定理2对于系统(2)，设计未知系统动态估计器器(6)，则估计误差eF=a(t)-(t)收敛于集合且 当k→0或ℏ→0时a(t)→(t).

证明：在式(2)的两侧应用低通滤波器(·)f=[·]/(ks+1)，则有

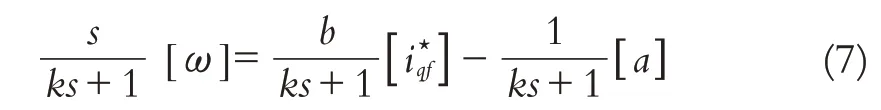
由式(7)和式(3)中的第一个公式可以知

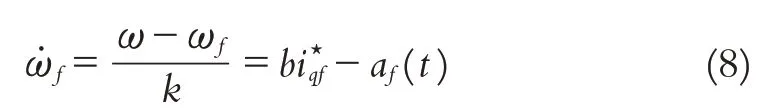
式中：af(t)是a(t)的滤波量，即然后，从式(6)和式(8)可以得出(t)=af(t).因此，估计误差可写为

根据式(11)可得解V(t)≤e-t/kV(0)+k2ℏ2/2，因此有故可进一步确定当k→0或ℏ→0时，有eF(t)→0成立.

2.1.2 速度控制器设计

将所提出的USDE应用到系统(2)的控制器设计中，以实现给定指令ω★的输出跟踪.含有估计器(6)的系统(2)可写为

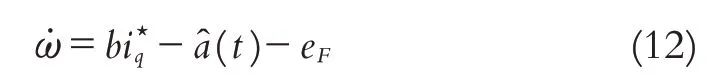
定义速度跟踪误差为

则速度环的复合控制律可设计为

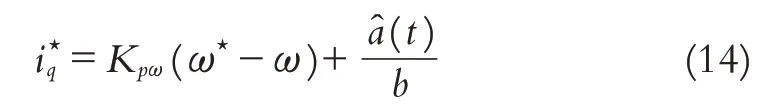
式中，Kpω＞0为速度环比例增益，ω★为参考速度，i★q为速度环输出.

根据文献[31]，可采用Lyapunov定理证明系统的稳定性[32].

定理3对于含有未知动态a(t)的电机系统(1)，设计基于估计器(6)的控制器(14)，则估计误差eF和速度跟踪误差e将收敛于零附近的一个小紧集，且

集合大小由supt≥0的界限决定.

证明：将式(14)代入式(12)，得到跟踪控制误差

由式(6)和式(14)可以得出基于USDE的速度控制系统，如图2所示.图中虚线框内为基于USDE的抗干扰速度控制器，它能抑制速度环路上的干扰，有效抑制速度波动，提高电机控制精度.且由前述证明可知，当减小滤波增益k和增大控制增益Kpw时，可缩小控制系统误差边界.

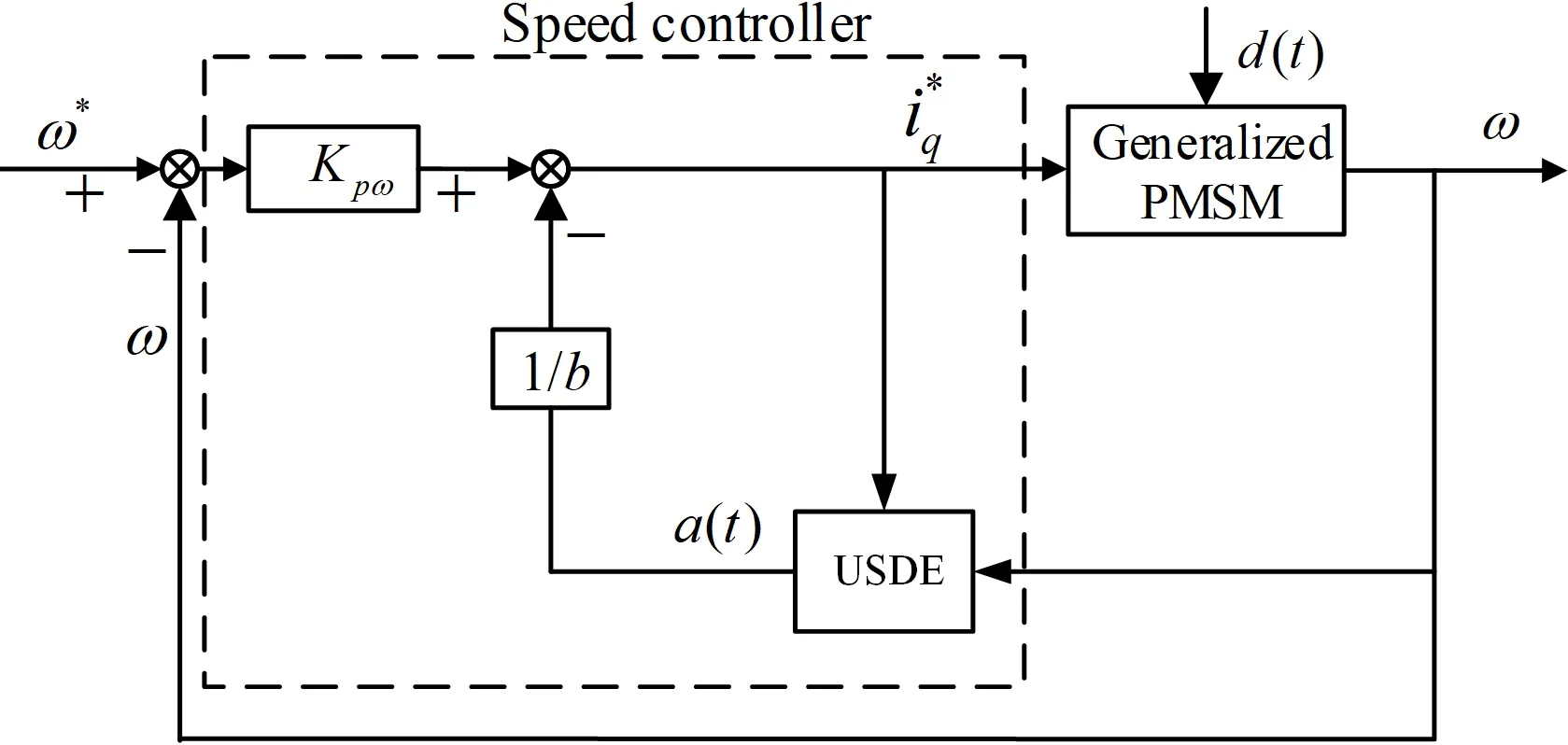
图2 基于USDE速度控制器的PMSM控制系统

2.2 基于未知系统动态估计器的电流环控制器设计

众所周知，PMSM电机控制中电流环受参数变化的影响，如定子绕组电阻、不精确的反电动势模型等，会降低PMSM控制系统性能[10].因为转矩环（即q轴电流环）控制的响应时间要比速度环响应时间更短，任何改善内环抑制参数变化措施都将直接且有效地改善整个系统的控制性能.为了抑制这些集总干扰造成的影响，将分别在d，q轴上使用基于未知动态估计器的复合控制来抑制电流环上的干扰和转矩波动，以提高电机控制精度.

PMSM电压方程为

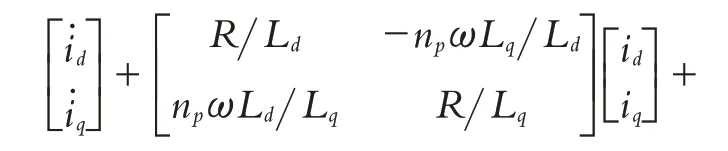
2.2.1 未知输入观测器设计

为克服集总干扰d的影响，定义q和U的滤波后的变量为qf和Uf，有

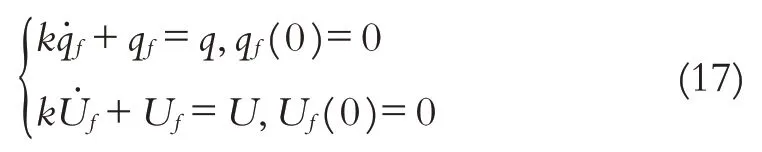
其中，k＞0为滤波器参数.

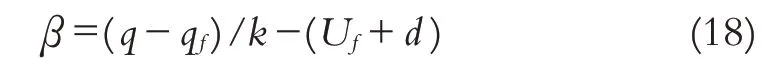
由文献[3]知，考虑系统(16)和滤波操作(17)，有最终一致有界，并对任意有限常数k＞0，公式lki→m0[lt→im∞{(q-qf)/k-(Uf+d(t))}]=0成立.该不变流形提供了从滤波变量qf,Uf到未知动态d(t)的映射.因此，可用于设计d(t)的估计器为

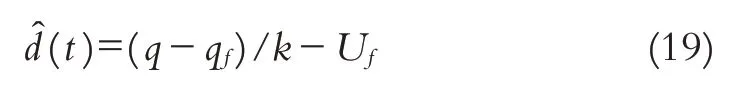
显然，设计者只需选择滤波常数k＞0.把q、Uf代入式(19)得

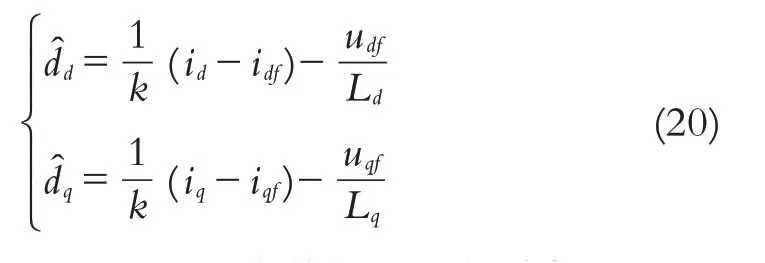
本文提出的观测器的收敛性可以归纳如下：

定理4对于系统(16)，设计未知动态估计器(19)，则 估 计 误 差ed=d-收 敛 于 集 合且当k→0或ℏ→0时d→成立.证明：在式(16)的两侧应用低通滤波器(·)f=[·]/(ks+1)，则有

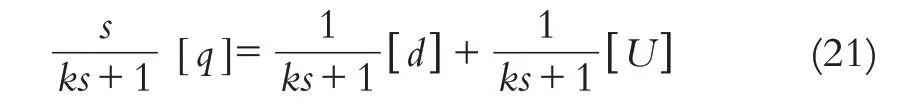
由式(21)和式(17)中的第一个公式可以知

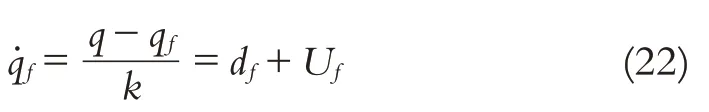
式中，df是d的滤波量，即从式(19)和式(22)可得=df，进而推导出估计误差为

根据式(25)得到解为V(t)≤e-t/kV(0)+k2ℏ2/2，因此进而可知当k→0或ℏ→0时，有ed()t→0成立.

2.2.2 电流控制器设计

把所提出的USDE应用到系统(16)的控制器中，具有估计器(19)的电流环复合的控制率设计为

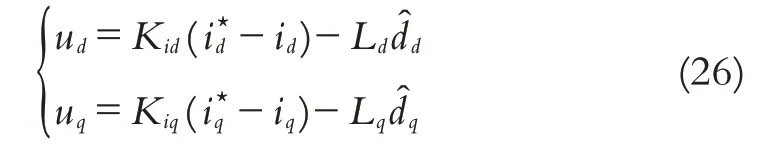
其中：Kid＞0,Kiq＞0为电流环比例增益，i★d,i★q为参考电流，ud,uq为电流环输出.式(26)分别是d、q轴的电流控制器.可类似文献[31]和前述速度环分析证明系统的稳定性，此处从略.

由式(20)和式(26)可以分别得出基于USDE的d、q电流控制器，将其应用到PMSM控制系统，如图3所示.图中两个虚线框分别为d、q轴电流控制器，它能有效且直接地抑制电流环上的集总干扰，减小电机输出电磁转矩的波动，提高控制系统精度.

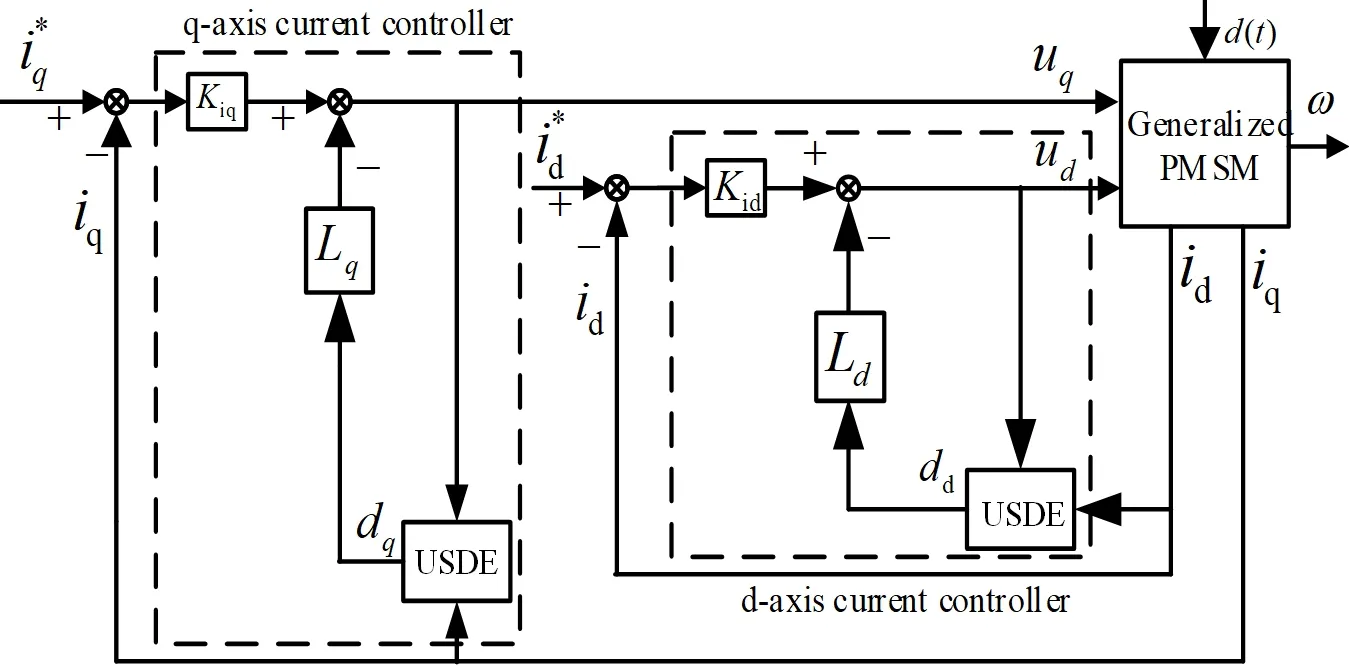
图3 系统的基于USDE的电流控制器

通过未知动态估计器设计了速度环和电流环的3个控制器，所构建的PMSM控制系统如图4所示.

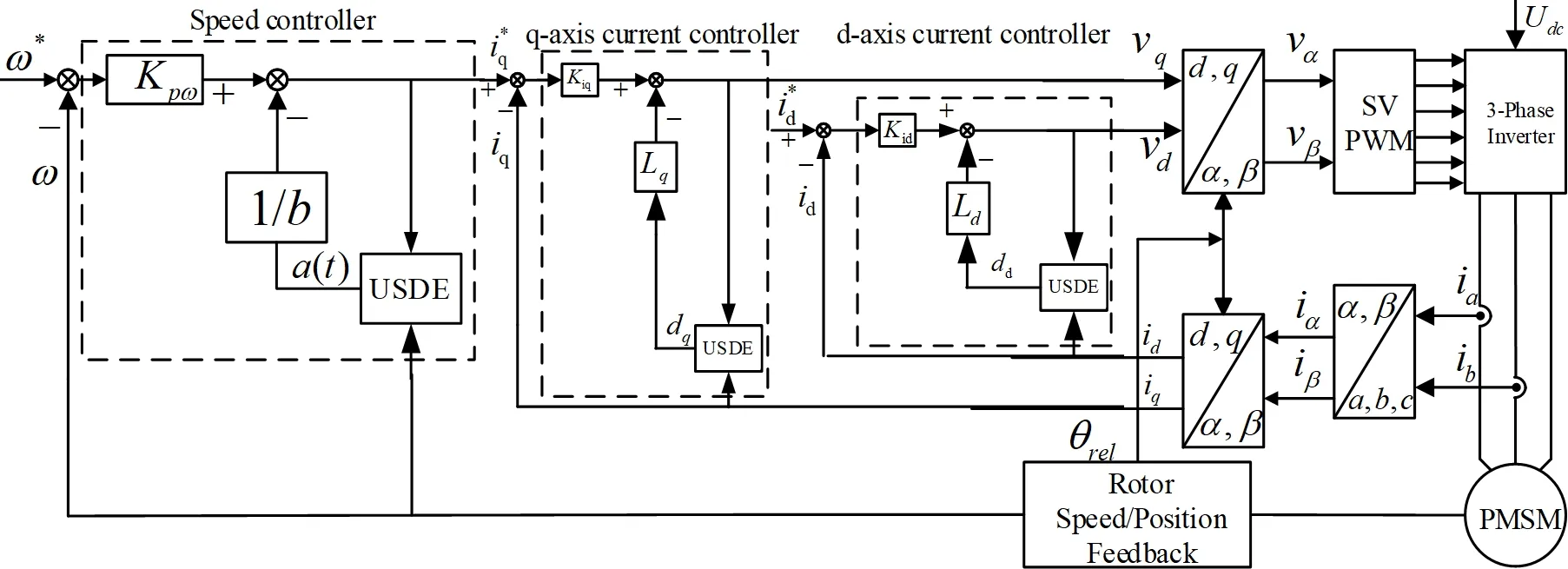
图4 基于USDE控制器下的PMSM控制系统

3 仿真结果及分析

在建立仿真模型时，本文调用了Simulink模块库中的PMSM模块、PI调节模块、三相两电平电压源逆变器模块，直流电压为300 V.PMSM仿真参数如表1所示.

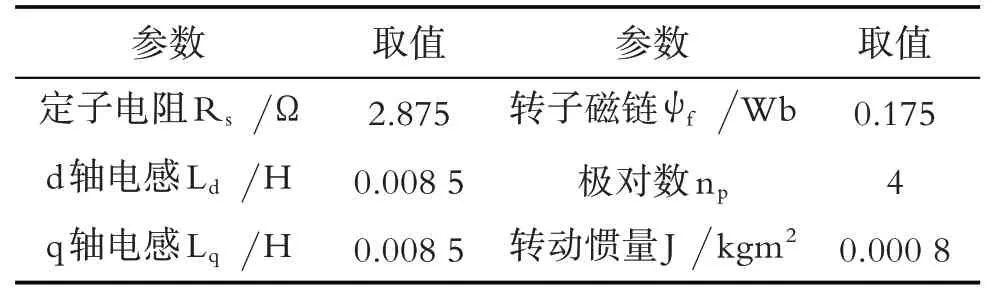
表1 仿真系统参数

图5至图7为PID控制器和含USDE复合控制器下的PMSM系统电流、转矩、转速仿真图，仿真时间位0.2 s，速度给定值为800 r/min，在0.1 s时加入负载2 N·m.为了仿真对比易于观察，在被控系统中加入正弦干扰d(t)=10sin(314t)，如图1系统框图中的干扰信号d(t).

由图5可以看出，由于系统干扰的存在，电机定子电流存在较大波动，尤其在电机启动时波动较大.通过图5刚启动时的局部放大图可以看出，USDE的补偿控制能获得更好的收敛性，且能减小电流的波动，而在PID控制下，启动时电流波动较大.稳定后，在未加负载时和0.1 s加入2 N·m负载后，电流有较大谐波.从图5稳定后局部放大图可以看出PID抑制电流畸变作用不大，黑实线部分谐波成分较大，虚线谐波含量要少于黑实线谐波含量，表明在含USDE的补偿控制下，电机系统有更好的电流波形，谐波含量明显少.

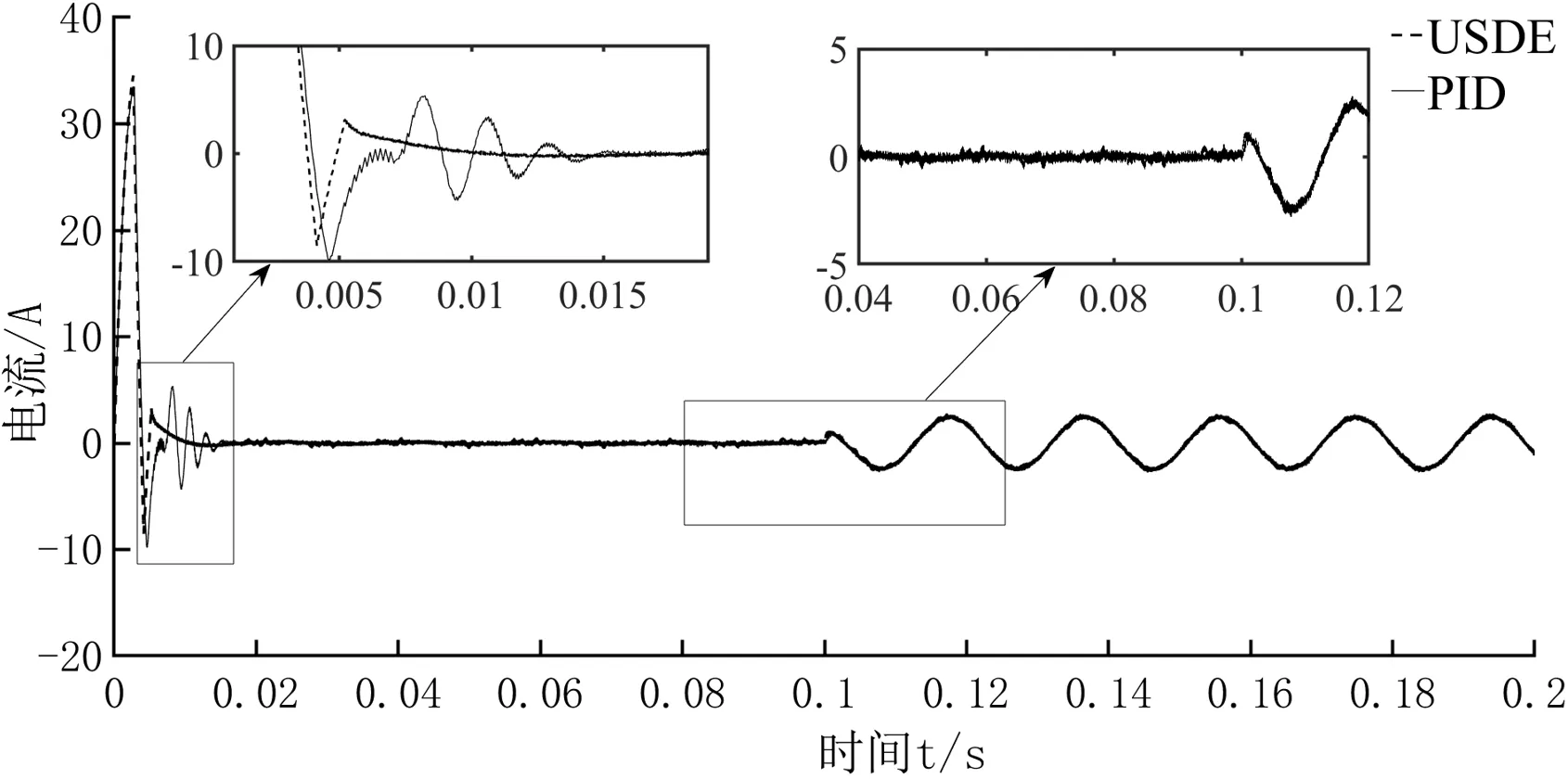
图5 定子电流波形图

通过图6电磁转矩图可以明显看出含USDE的复合控制能使得系统转矩波动更小，尤其在0.1 s加入转矩干扰时候效果更佳.图7为两个控制算法下的转子转速波形对比图，可以看出系统加入正弦干扰后，电机启动时，速度波动较大，后又趋于稳定，这是由于系统启动时，因为电流等状态变量发生变化，引起速度环上的干扰增加，导致电机转速产生波动.通过速度图及其局部放大图对比可知，含USDE复合控制下的PMSM系统速度在启动时，能够快速收敛到800r/min，之后稳定在800r/min，而PID控制下的速度在800r/min附近波动，这是由于加入了正弦干扰所致.综合可见，含USDE的复合控制系统在速度控制抗干扰能力要优于PID控制.

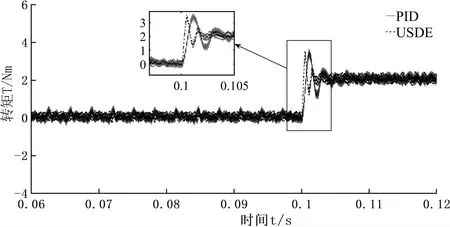
图6 转矩波形图

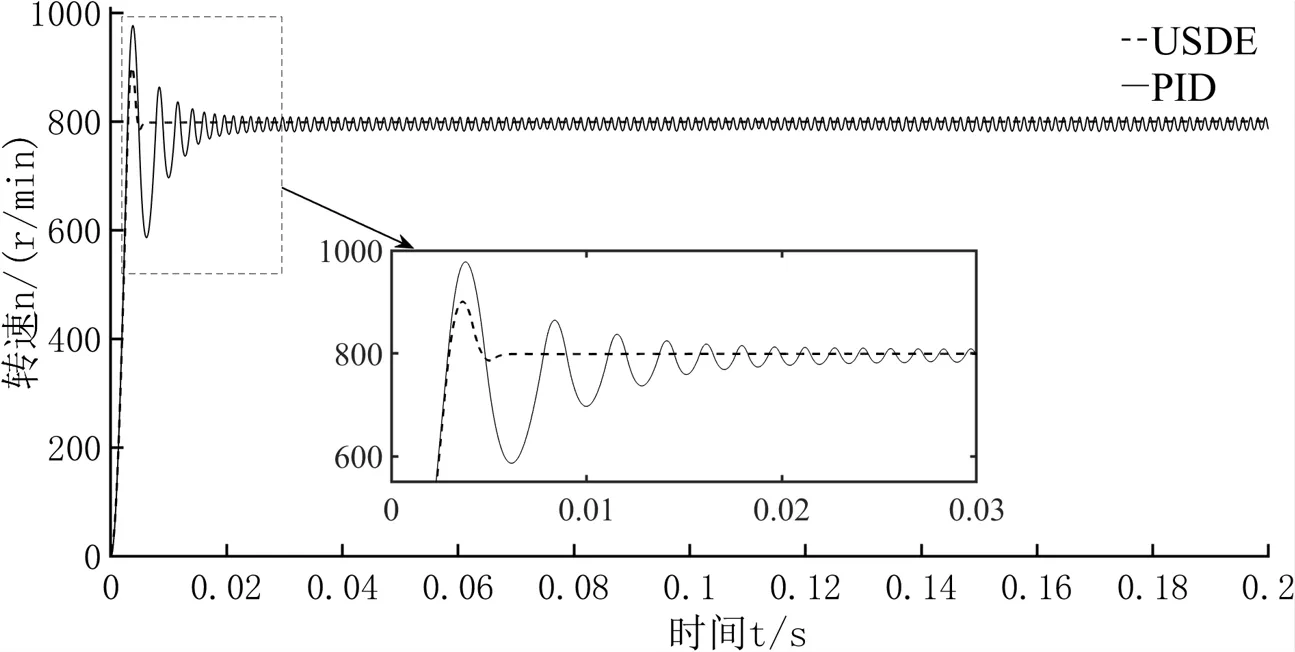
图7 转速波形图

可见，本文提出的基于USDE控制方法能够抑制PMSM控制调速系统中的干扰，不论是电流的谐波干扰，还是负载突变引起的速度、转矩波动等干扰都能被有效抑制.

4 结语

本文设计了一种基于未知系统动态估计器的永磁同步电机速度控制方法.对比传统的PID控制方法，其在抑制系统动态干扰方面更有优势.将含有USDE的复合控制策略应用到PMSM速度控制系统中，可形成一个有效的PMSM矢量速度控制系统.最后通过仿真分析了整个系统的稳定性和控制误差的收敛性能，并开展了对比仿真验证.本文方法可为高精度电机控制提供一个实用且简单有效的新思路.