利用微波遥感数据进行森林生物量两种模型反演
陈 磊,薛东剑,代 优
(成都理工大学地球科学学院,四川成都 610059)
森林是碳储藏库和衡量生态系统平衡的关键指标之一,准确估测森林地上生物量(above-ground biomass,AGB)对于了解气候变化、维持生态系统平衡具有不可代替的作用[1-3].同时,林业是国家经济发展的重要组成部分,森林储蓄量是衡量国家林业资源的关键指标,进行森林地上生物量估测,具有重要的自然和社会经济价值[4].传统的森林地上生物量估测方法主要以野外实地测量为主,此方法虽然精度高、估测准确,但因其耗时、耗力、耗材且在偏远山区和地质条件复杂的地区难以实施,难以运用在连续大范围的生物量监测[5]方面.随着遥感技术不断发展,借助其高效、动态、宏观优势快速获取各个尺度的森林参数,已成为区域或全球大尺度森林资源动态监测和定量评价的重要工具[6].
利用光学遥感、激光雷达和微波遥感数据结合实测样地数据进行森林地上生物量反演已成为国内外学者研究的热点并取得了显著成果[7-10].合成孔径雷达(Synthetic Aperture Radar,SAR)技术,波长较长,对森林有一定的穿透能力,能有效获取森林树干结构特征,且具有全天时、全天候大范围连续动态监测等优点,弥补光学遥感和激光雷达的缺点,在森林地上生物量反方面具有巨大潜力[11-14].陈尔学[15]等利用SIR-C/X两个波段的SAR数据,采用极化干涉测量数据处理方法和树高反演算法,应用于平均树高的提取;张国飞[16]等利用Sentinel数据通过线性回归和机器学习算法估测了滇池湖滨森林地上生物量.除了数据源,森林地上生物量反演方法的选择也十分关键.参数化方法主要是基于数理统计的线性回归方法,谭炳香、李增元[17]等利用Hyperion高光谱数据采用逐步多元线性回归定量估测森林郁闭度,精度达到86.34%.Kronseder[18]等利用全波形激光雷达数据建立多元线性回归模型应用于热带森林地上生物量的估测,解释了样地71%的变化.潘磊[19]等以Sentinel-1 SAR数据的纹理信息构建回归模型估测森林生物量,R2达到0.716.非参数化方法主要是通过建立实测数据和特征变量的非线性关系而实现的,菅永峰[20]等基于GF-2和SPOT-6卫星的纹理信息和光谱信息构建随机森林模型,两者精度分别为R2=0.88、R2=0.89.陈尔学[21]等利用Landsat TM数据采用K最近邻法(K-NN)对小面积统计单元森林蓄积进行了估测,平均误差低于1.5 m3·hm-2;Gleason[22]等利用机载激光雷达数据,对比分析线性混合效应(LME)回归、支持向量机(SVR)和Cubist四种建模技术在生物量估测上的有效性.
本文以Sentinel-1 SAR为数据源,分别提取VV、VH极化下的后向散射系数和四个不同大小窗口下的纹理特征,结合坡度、坡向、高程三个地形信息,采用多元线性回归和随机森林进行建模反演,对比分析两种模型的精度,以探索采用微波遥感数据和非线性方法在森林地上生物量反演上的能力.
1 研究区概况
研究区位于美国弗吉尼亚州东南部和北卡罗来纳州东北部,地理位置为36°26′-36°46′N、76°34′-76°21′W,面积约637 km2,距离大西洋海岸不到64 km.迪斯默尔沼泽属于副热带湿润气候,年均温19℃,年平均降水量为(117~137)cm,地形以平原为主,地势平坦、起伏小.研究区及实测样地数据如图1所示.
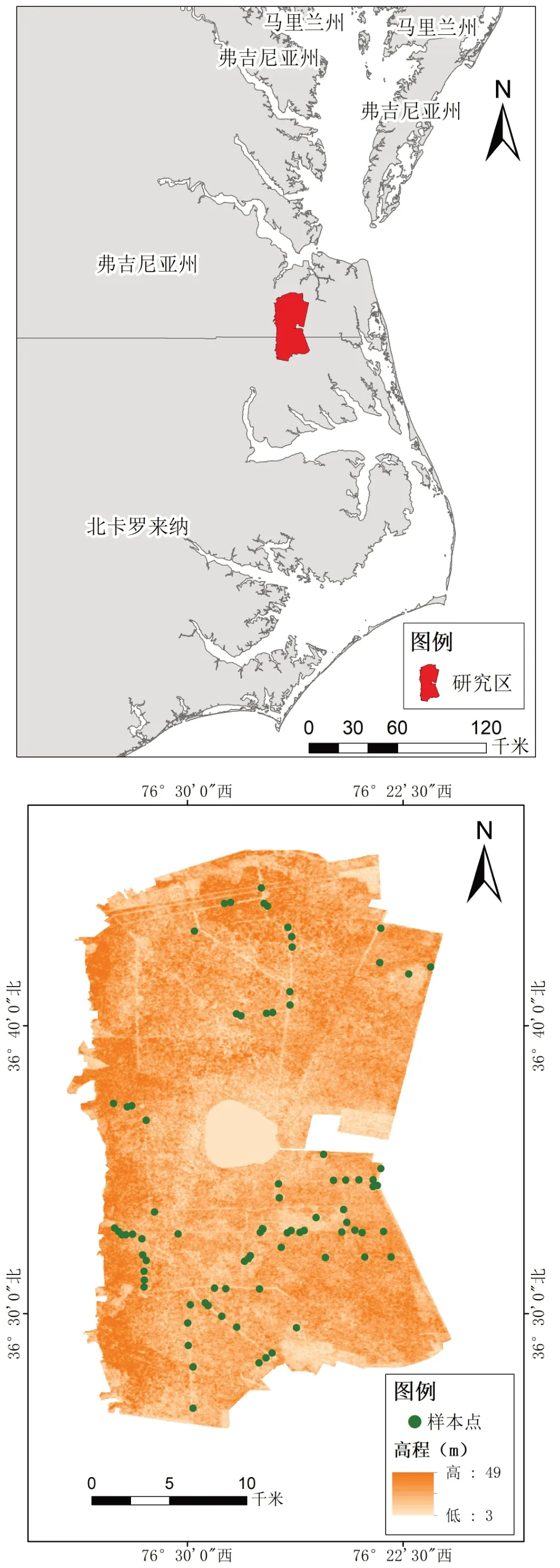
图1 研究区位置及样地分布图
2 材料与方法
2.1 数据来源
(1)雷达数据及处理.采用的Sentinel-1A数据来源于欧空局,影像成像时间为2015年9月18日,数据类型为干涉宽幅模式(IW)斜距单视复数(SLC)影像,极化方式为VV、VH,空间分辨率为5 m×20 m,入射角为43.99°.对Sentinel-1 IW SLC影像进行精密轨道校正、多视处理、Frost滤波处理,利用ASTGTM2 30 m分辨率的DEM进行地形校正、辐射定标和地理编码,最后将图像转换为以分贝为单位的后向散射系数图.
(2)样地调查数据.研究区样地调查数据来源于美国地质调查局于2014年夏季收集地块级现场数据,使用Trimble ProXH全球定位系统(GPS)记录每个样地的中心位置,并进行差分校正.每块样地的半径设置为5.6 m,共计83块样地调查数据.
2.2 特征提取
(1)纹理特征:影像纹理特征提取采用灰度共生矩 阵(GLCM),GLCM于20世 纪70年 代 由Haralick[23]等人提出,它是图像像元之间的角度和距离二者的函数,该矩阵中的值表示的是图像中某个像元与某一个距离和方向处指定像元的像元值出现的次数.本研究采用4个不同大小的窗口(3×3、5×5、7×7、9×9)下的4个不同方向:0°(从左到右)、45°(从左下到右上)、90°(从下到上)、135°(从右下到左上)来计算8个常用纹理变量.
(2)地形特征:利用DEM数据分别提取坡度、坡向、高程三个特征.
本研究提取了VV、VH后向散射系数,VV、VH极化下4个窗口的8种纹理特征,坡度(Slope)、坡向(Aspect)和高程(Elevation)三个地形特征,共计69个特征.特征变量类型、名称和个数见表1.
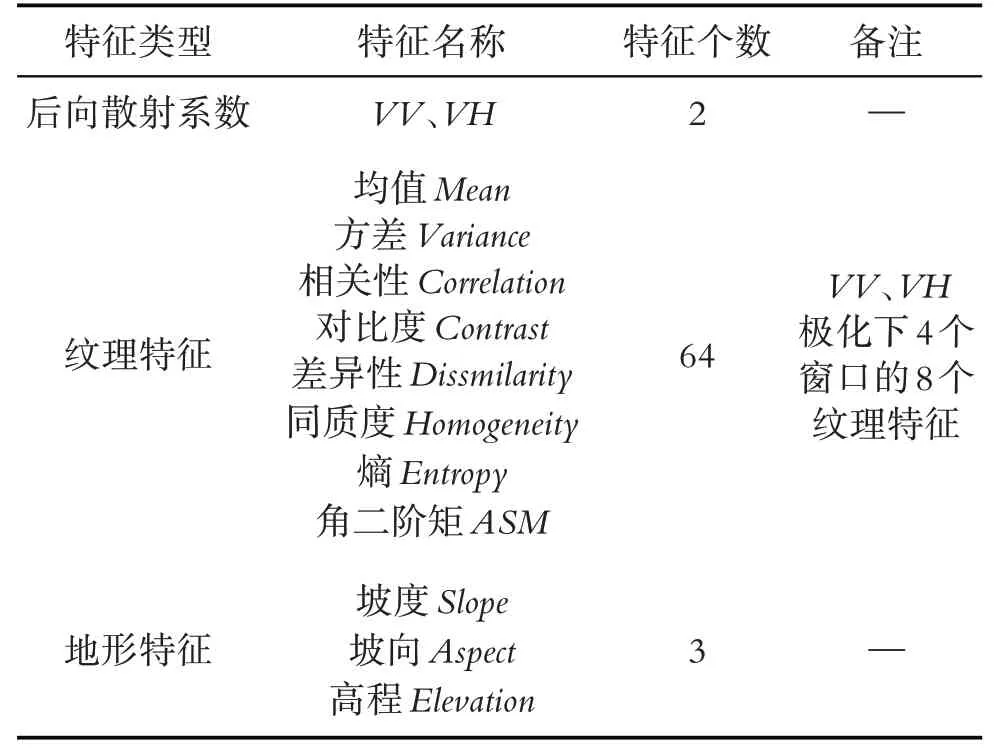
表1 特征变量因子
2.3 生物量估测方法
2.3.1 多元线性回归模型
回归分析的目的是分析两个或两个以上的变量间是否存在相关性以及相关方向和强度.构建多元线性回归模型的任务主要包括:根据多个响应变量和解释变量的实测值来构建线性方程;分析各个响应变量对解释变量的综合线性影响显著性;评价各个响应变量与解释变量的相关性及各个响应变量之间的共线性;选择出对解释变量有显著影响的最优解释变量建立回归模型.多元线性回归模型的一般表达式为:
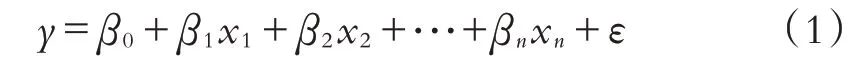
其中,y为生物量实测值,x1,x2,···,xn为特征变量,β0为常数,β1,β2,···,βn为回归系数,n为预测变量个数,ε为误差项.
2.3.2 随机森林模型
随机森林(RF)是由Breiman[24]于2001年提出的一种基于决策树的分类、回归算法,由于随机森林每颗决策树都随机地选择部分样本和部分特征,故该模型可以很好地避免过拟合问题,具有很好的抗噪能力和较好的稳定性,适合并行计算且运算速度和精度都较高.随机森林通过自助法bootstrap重采样技术,从原始训练样本集中随机有放回的抽取2/3样本生成新的训练集合训练决策树,同时从所有特征中选择m个特征来确定决策树节点,按照以上步骤生成n颗决策树组成随机森林.该模型需要调整的参数为决策树的数目(ntree)和节点分类时的变量个数(mtry).经多次运行,根据决策树数目和误差之间的关系图确定最优的数目和变量个数.
2.3.3 模型最优特征变量的选择
在多元线性回归和随机森林两个模型中选择出最优的特征变量进行建模是决定预测精度的重要因素.使用逐步回归法选择多元线性回归模型的最优特征变量,随机森林法选择随机森林模型的最优特征变量.
逐步回归的思想是将变量逐个引入模型,每引入一个解释变量后都要进行F检验,并对已经入选的解释变量逐个进行t检验,当原来引入的解释变量由于后面引入的解释变量变得不再显著时,则将其删除,以确保每次引入新的变量之前回归方程中只包含显著性变量.此过程直到既没有显著的解释变量选入回归方程,也没有不显著的解释变量从回归方程中删除为止,以保证最后所得到的变量集是显著的、最优的.
随机森林算法对解释变量重要性进行度量,选择出重要性高的解释变量.随机森林使用Inc-NodePurity(Increase in Node Purity)值对解释变量重要性进行排序,通过残差平方和来度量,其代表了每个变量对决策树每个节点上观测值的异质性的影响,该值越大表示变量重要性越高.
3 结果与分析
3.1 最优变量选择结果
利用逐步回归法和随机森林法进行最优变量选择的结果见表2.其中,逐步回归法选择出的变量按照进入顺序进行排列,随机森林法选择出的变量按照重要性进行排列.

表2 最优变量选择结果
由表2可知,在地形信息中,两种方法均筛选出坡度(Slope)作为最优变量,且重要性大于其他所有特征;VV极化下的纹理特征更多地参与到森林地上生物量反演建模中.坡度(Slope)信息对于森林生物量估测具有重要作用,VV极化下的纹理特征在森林生物量估测中更具有稳定性,地形信息和微波遥感提取的纹理特征在生物量反演中具有较大潜力.
3.2 模型的构建
多元线性回归模型:根据逐步回归法选择出的最优变量作为自变量,实测样地生物量作为因变量构建回归模型,即:

随机森林模型:根据决策树数目和误差之间的关系图选择最优的数目.经过多次调试,根据图2,当决策树数目为300以后,误差趋于平稳,将随机森林法选择出的最优变量代入模型进行建模反演.

图2 决策树数目和模型误差关系图
3.3 模型精度评价
为定量分析参数和非参数模型在森林地上生物量的反演精度,进行多元线性回归模型和随机森林模型的反演,结果见图3.多元线性回归模型的预测结果较为离散,R2为0.458,均方根误差(RMSE)为65.822 t/hm2,预测精度较差;随机森林模型的预测值和实测值较为吻合,R2为0.697,均方根误差为43.957 t/hm2,预测精度较好.因此,随机森林模型在森林地上生物量预测上效果更好.
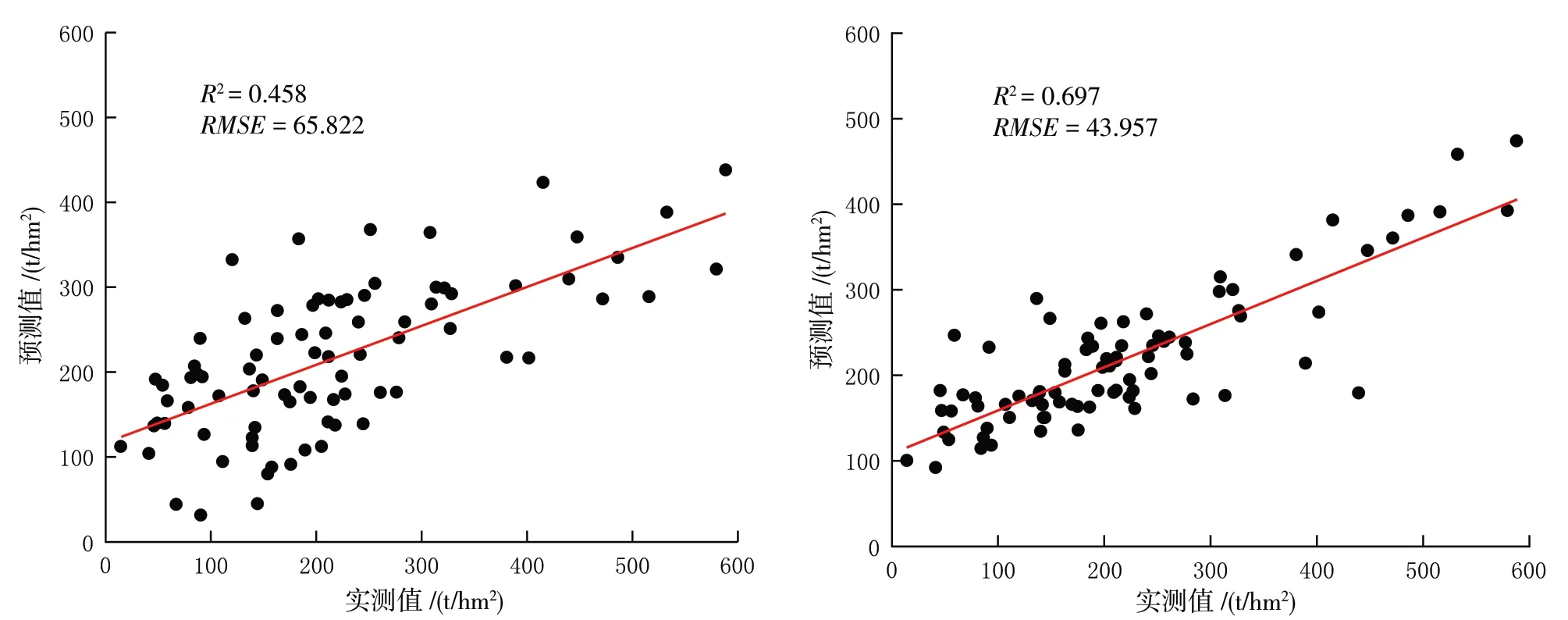
图3 多元线性回归模型(上)和随机森林模型(下)预测结果
从两个模型的预测值和实测值的比较可以看出,两种模型都存在对低生物量过高估计,对高生物量过低估计的问题.基于多元线性回归模型的森林地上生物量预测值最低为31.68 t/hm2,最高为438.08 t/hm2,与之对应的实测值为90.18 t/hm2和588.35 t/hm2,弹性幅度较大,表现出明显饱和的特点,该模型各组数据相对误差较大.基于随机森林模型的森林地上生物量预测值最低为91.97 t/hm2,最高为473.8 t/hm2,与之对应的实测值为41.34 t/hm2和588.35 t/hm2,当生物量小于150 t/hm2和大于270 t/hm2时,相对误差最大,平均相对误差为61.03 t/hm2,生 物 量 在150 t/hm2和270 t/hm2之 间时,相对误差最小,平均相对误差为6.69 t/hm2.
4 结语
本文以美国迪斯默尔沼泽国家野生动物保护区为研究对象,利用Sentinel-1 SAR数据对比分析随机森林和多元线性回归模型在生物量反演中的精度.随机森林方法相比于多元线性回归方法更适用于森林地上生物量反演.多元线性回归方法以数理统计为理论基础,便于分析解释变量和响应变量之间的线性因果关系,但难以描述森林地上生物量与遥感数据间复杂的非线性因果关系,容易造成估测值与实测值之间的偏差过大.随机森林方法不依赖于特定的函数分布,能够有效的在大数据集上运行,处理高维度数据,不容易出现过拟合问题,可以对变量重要性进行排序,既提升了变量特征选择效率,又提高了森林地上生物量估测精度.

