非对称荷载下含中心孔洞煤岩变形损伤特性与本构模型

王 涛,葛丽娜,赵洪宝 ,张向阳,张 欢,李文璞

(1. 太原理工大学 安全与应急管理工程学院,山西 太原 030024;2.中国矿业大学(北京) 能源与矿业学院 北京 100083;3.安徽理工大学 煤矿安全高效开采省部共建教育部重点实验室,安徽 淮南 232001;4.辽宁工程技术大学 建筑与交通学院,辽宁 阜新 123000)

应力诱发岩石变形破坏问题是岩土工程、采矿工程中经常遇到的问题[1-2]。在一些特殊工况下，岩石受赋存环境或开采扰动影响会经历非对称荷载环境下的变形与损伤过程[3-4]。例如，由于隧道上覆山体的起伏，隧道开挖后周边岩体会受到上覆岩层自重引起的非对称荷载作用；井工开采中，上层煤开采遗留的保护煤柱也会导致下层煤开采时工作面运输巷道受到非对称荷载的作用。因此，研究非对称荷载下煤岩体的强度变形行为和裂纹扩展行为对于了解煤岩体的断裂机制和预测岩石工程中的地质灾害尤为重要。

隧道、采矿和水利工程中经常需要进行岩体开挖，在岩体开挖过程中必然对围岩造成损伤和破坏。开展孔洞周边围岩破裂过程的研究有助于揭示围岩损伤破裂机理，并基于此为评估开挖工程围岩的稳定性提供理论基础。赵洪宝等[5]开展了局部荷载作用下含孔洞原煤与型煤单轴压缩试验，对比分析了2种煤样裂纹演化规律的差异性。YANG等[6]开展了含圆孔节理岩体的单轴压缩试验与数值模拟试验，认为根据节理倾角的不同，可将节理与中心孔洞裂隙贯通模式分为3类。腾俊洋等[7]研究了锚杆对含孔洞岩石的力学特性与裂纹扩展规律的影响，认为锚杆形成的锚固区可以弱化岩石裂纹的发展、改变裂纹扩展路径。LI等[8]开展了动静耦合载荷作用下含孔砂岩的断裂过程研究，发现静态加载显著影响表面裂纹的萌生，以及破坏区域的形状和大小，孔周围的应力集中和静载产生的远场应变共同作用促进了岩石的冲击损伤。WU等[9]、CHEN等[10]分别从试验与模拟角度研究了孔的形状对岩石变形、破裂过程的影响，认为孔的形状不同对岩石力学性能折减程度不同，不同形状孔周边均会出现4类裂纹，孔的形状会影响裂纹的出现顺序、起裂位置、扩展特征。韩观胜等[11]研究了含不同孔径双孔洞岩石单轴压缩过程中的力学特性，探讨了次孔洞直径与两孔洞相对位置的变化对岩石力学参数、裂纹演化规律的影响。WU等[12]借助于DIC方法研究了单轴压缩过程中含孔砂岩的变形损伤过程，试验结果表明岩石表面变形场可以直观地显示裂纹演化过程，含孔试样在单轴载荷作用下的破坏是由剪切裂缝和板状裂隙贯通引起的；ZHU等[13]借助于DIC与AE方法，对填充不同夹杂物的预制孔砂岩的变形损伤过程开展研究，认为岩石的力学行为、表面应变场与AE信号具有良好一致性，DIC和AE技术均能揭示试件的断裂演化过程。LIU等[14]利用DIC方法研究了2个椭圆孔洞和4个裂纹对砂岩力学行为的影响，得出应变局部化区域是裂纹萌生的标志，裂纹扩展行为是应变局部化区域的渐进演化结果，描述了裂纹的聚结模式，确定了4种裂纹的聚结模式。

建立岩石的损伤模型对分析和预测岩石工程材料的变形特性具有重要意义，如何建立试验获得参数与力学参数的定量关系并预测岩体失稳破坏仍是岩石力学研究的热点和难点。李波波等[15]开展了不同瓦斯压力下煤岩三轴压缩试验，通过得到的瓦斯压力与黏聚力关系修正了Mohr-Coulomb准则，建立了含瓦斯煤损伤本构模型。WANG等[16]认为煤岩受载过程中产生的电磁辐射是材料内部微损伤的结果，建立了电磁辐射脉冲数与损伤变量的关系，给出了基于电磁辐射脉冲数的煤岩损伤模型。SONG等[17]借助于DIC方法观察了砂岩试件的损伤演化和裂纹扩展过程，提出采用表观应变的偏差计算损伤因子的方法，实现了采用DIC方法定量表征岩石损伤演化过程。

各国学者就完整岩石或含预制裂隙或孔洞岩石的力学特性和损伤破断规律开展了大量的研究，并取得了丰硕的研究成果。但是，已有研究成果均是基于常规单轴压缩或三轴压缩等均布荷载条件下得到的，而关于非对称荷载下岩石的变形与损伤规律的研究鲜见报道。因此，笔者以硬脆性原煤试样与软塑性型煤试样为研究对象，借助于数字散斑方法，开展了非对称荷载与预制圆孔共同影响下不同硬脆性材料的变形场演化与损伤演化规律，研究成果可为偏压条件下隧道或巷道的变形失稳解释与支护设计提供依据。

1 试验方案与设备介绍

1.1 试样制备

试验中采用含中心孔洞的原煤与型煤2种试样，对比非对称荷载下2种具有不同力学特性试样的变形损伤规律。原煤大块取自霍州煤电集团干河矿，将煤块包装好后运至实验室，经过切割、打磨制备而成，煤样加工过程严格按照美国试验与材料协会推荐的标准执行，制备的原煤试样为边长70 mm的立方体，立方体试样制备完成后借助于手持式电钻在试样中心钻凿直径为8 mm的中心孔洞。采用DIC方法开展变形场监测的前提是制备良好的散斑场，为了提高试样表面的散斑对比度，消除煤样表面原生晶体对散斑效果的影响，首先用自喷漆将煤样表面喷涂成黑色，待黑色漆面干燥后再向其表面随机喷涂白色斑点。

型煤试样由煤粉二次压缩而成，将现场取回的煤块破碎、筛分获取粒径在1 mm以下煤粉备用，将煤粉、水泥、水按一定比例搅拌均匀，将混合物放入型煤制备装置，以20 MPa恒压20 min后脱模，脱模后的型煤在养护箱养护28 d后即可达到试验要求。型煤试样中心孔洞与散斑场的制作方法与原煤试样一致。试验中使用的原煤与型煤试样如图1所示。

1.2 试验方案

为了研究荷载非对称程度对含中心孔洞原煤与型煤试样变形损伤的影响，采取了图2所示的4种加载方式，通过移动刚性加载板的位置实现不同程度的非对称荷载作用。由图2可知，本次试验共采取了4种加载方式，分别为4S/4,3S/4,2S/4,S/4，其中S为试样表面积。每种加载方式下原煤与型煤试样均开展3组平行试验，共需原煤试样12块，型煤试样12块。

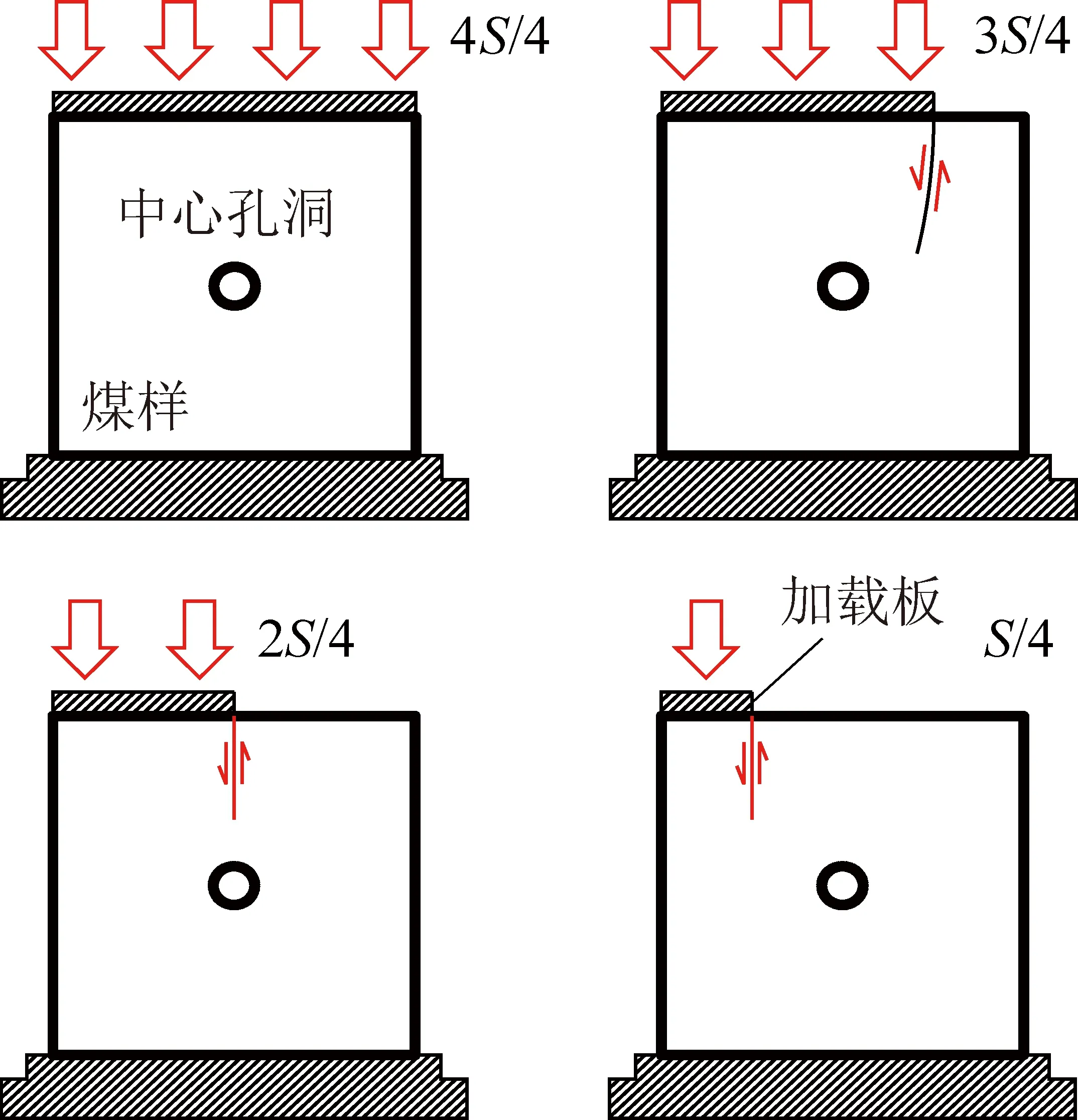
图2 加载方案示意Fig.2 Loading schematic diagram

试验中采用的设备如图3所示。采用MTS电子伺服试验机对煤样开展压缩试验，采用位移控制模式，加载速度设定为0.1 mm/min；加载过程中采用数字散斑系统实时捕获煤样表面散斑场的变化，数字散斑系统包括德国Basler公司生产的404 K面阵黑白工业CCD相机(分辨率：2 352 pixel×1 720 pixel)及配套使用的焦距为105 mm的镜头，2台LED补光灯，1台计算机操作系统。为了更加准确地捕捉煤岩破裂过程，试验过程中相机的采集与存储速率设定为15帧/s，标定得到的物面分辨率为0.05 mm/pixel。前期研究成果表明，采用上述设备与试验参数能够有效地获取煤岩表面变形场信息。首先，将补光灯放置于合适的位置，试验过程中保持煤样表面光照充分且受光均匀；其次，将CCD相机放置于试样前方，调整相机方位，使得相机靶面与煤样表面相互平行，调整焦距，使得煤样占据整个靶面，连接CCD相机与计算机，使试验过程中相机拍摄的照片能以数字信号传输至计算机；最后，利用基于DIC方法编写的图像处理程序获得不同加载时刻煤样表面位移场与应变场云图。

图3 试验系统Fig.3 Testing system

2 结果分析

2.1 应力应变特征分析

定义荷载非对称系数为非加载区面积与加载区面积的比值，即

(1)

式中，λ为非对称系数，0≤λ<1，λ=0为均布荷载；SL为荷载直接作用面积；S为试样表面积。

非对称荷载作用时，试样上表面为局部加载，试样应力计算时采用等效面积的办法，应力计算公式为

(2)

式中，σ′c为非对称荷载加载时试样应力；σc为均布荷载压缩时试样应力；α为相对加载面积，α=1,2,3,4。

根据式(2)对不同非对称荷载条件下煤岩应力进行计算，图4给出了不同非对称系数条件下煤岩应力应变曲线。由图4可知，非对称荷载作用时煤岩应力应变曲线与均布荷载作用时应力应变曲线均表现出典型的阶段性特征，主要包括初始压密阶段、线性变形阶段、塑性屈服阶段与破坏后阶段。初始压密阶段2种煤样应力应变曲线均呈上凹状，该阶段原煤试样主要发生初始孔、裂隙的压密，而型煤试样主要表现为颗粒相对错动导致的颗粒间孔隙减少；线性变形阶段，2种煤样的应力随着应变的增加均呈线性关系增加，其中原煤试样仍表现为原生裂隙的进一步压密，内部基本没有损伤的发生，卸载后试样的变形能够恢复，为线弹性阶段，而对于型煤试样来说，由于其颗粒间黏聚力较小，该阶段已出现颗粒间相对错动，卸载后变形不能恢复，为线性变形阶段；屈服阶段，原煤与型煤试样应力应变曲线均表现为上凸形；进入屈服变形阶段，原煤试样内部微裂纹持续扩展、演化，发生塑性变形，曲线下弯特征没有型煤试样明显，且临近破坏时刻，原煤试样表现为间断性的颗粒弹射现象，峰值时刻原煤发生崩解呈碎块状，表现出硬脆性特征，型煤试样主要发生内部细观颗粒的拉伸或剪切破坏，裂纹稳定扩展至试样破坏，表现为软塑性特征。

由图4可知，随着荷载非对称程度的增大，2种煤样峰值应力均逐渐减小。图5给出了煤岩峰值应力与非对称系数关系曲线，由图5可知，随着非对称系数的增加，煤岩峰值应力逐渐降低，2者大致呈线性函数规律。由此可知，荷载非对称程度越高，煤岩越容易发生破坏。

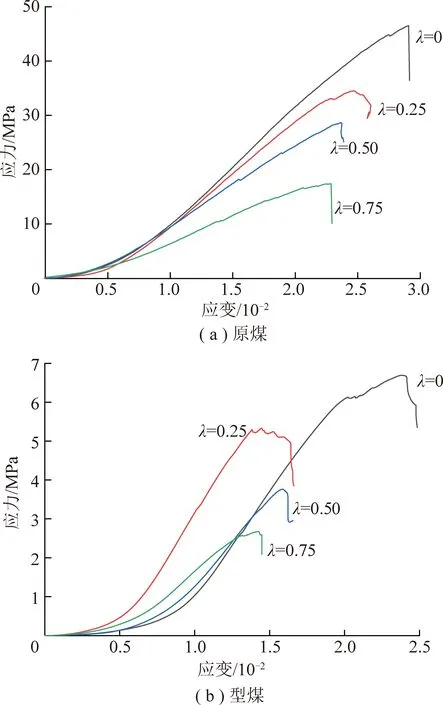
图4 不同非对称系数下煤岩应力应变曲线Fig.4 Stress-strain curves of coal and rock under different asymmetric coefficients

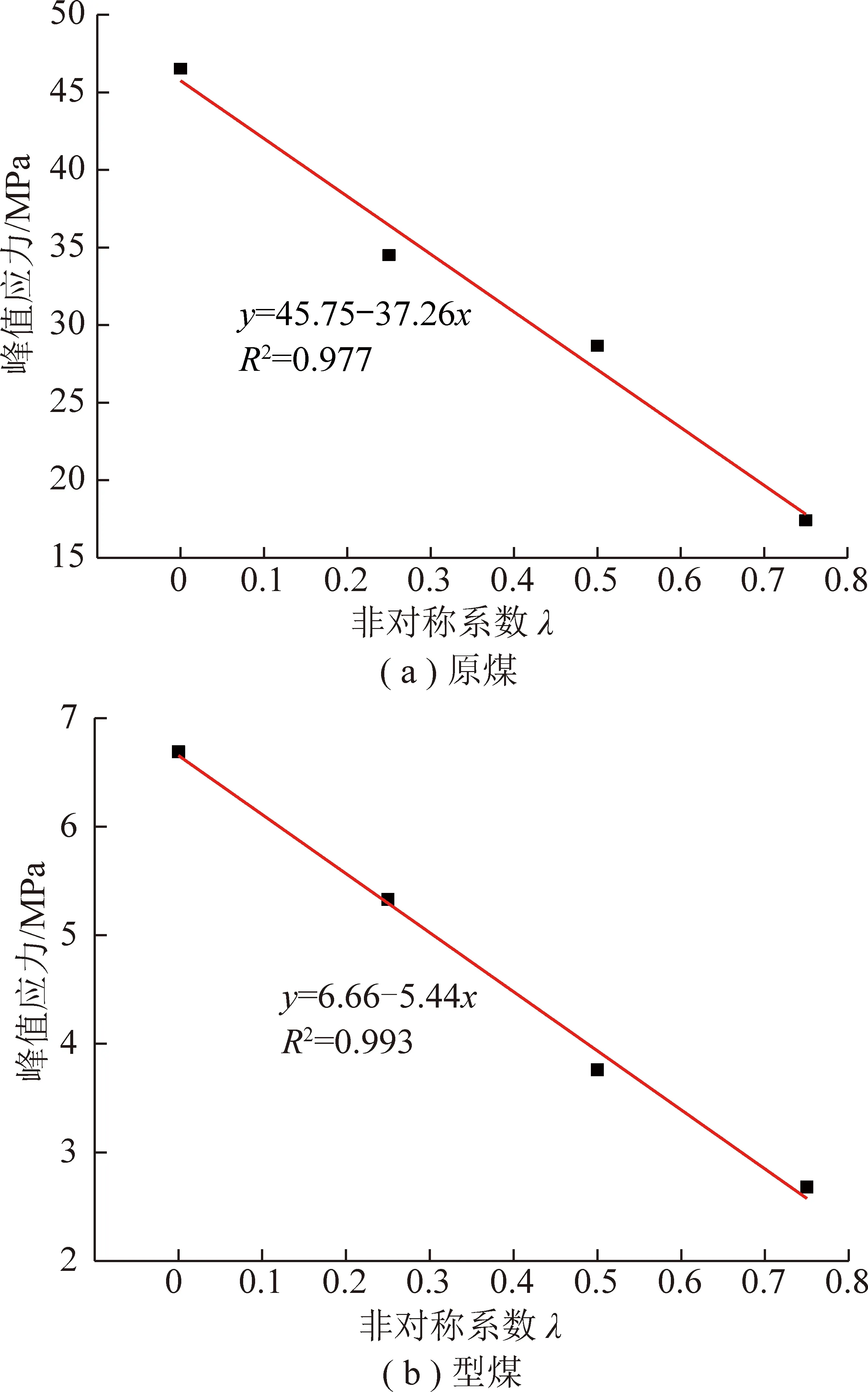
图5 峰值应力与非对称系数关系Fig.5 Relationship between peak stress and asymmetric coefficient

2.2 应变场演化规律分析

为了对比分析原煤与型煤的应变场演化规律，根据煤岩应力应变曲线特征，在其不同加载阶段各选取一个典型观测点位，计算给出了各观测点煤岩表面最大剪切应变(γmax)场云图。

图6为λ=0时不同加载时刻原煤与型煤最大剪切应变场云图，初始压密阶段，试样表面均有变形的发生，原煤试样表面高应变值区域呈散乱分布，而型煤试样主要集中在中心孔洞附近。中心孔洞可看做煤样的初始损伤，原煤试样孔裂隙较为发育，压密阶段表现为原生裂隙的闭合和中心孔洞的受压变形，型煤试样制作过程中孔裂隙已基本压密闭合，压密阶段表现为中心孔洞的变形。随着荷载的增加，高应变值先在中心孔洞周边集中，后继续向孔外侧扩展，形成应变局部化带，应变局部化带的演化过程能够反映出表面裂纹的演化过程，原煤试样破坏后块体呈三角锥形，应变局部化带呈近X型分布，表明原煤主要发生剪切破坏；型煤高应变值先在中心孔附近集中，后向型煤顶、底部扩展，另外，在远离孔的位置形成了一条与加载方向近似平行的应变局部化带，结合表面裂纹的形态，型煤试样主要发生拉伸-剪切破坏。

图7为λ=0.25时，不同加载时刻原煤与型煤最大剪切应变场云图。初始压密阶段，由于荷载非对称程度较小，荷载非对称性对煤样表面变形场分布影响不大，原煤与型煤表面应变分布规律与均布荷载条件下类似；随着荷载的增加，煤样表面高应变值分布向直接加载区与中心孔洞周边集中，局部化现象逐渐显现，最终形成的局部化带连接加载板端部的应力集中区与中心孔洞；原煤与型煤应变场的演化规律基本一致，所形成的应变局部化带形态也基本一致，且应变局部化带位置与表面主控裂纹分布位置基本吻合，结合煤样受力特征，该条件下原煤与型煤为宏观剪切破坏。

图7 λ=0.25时原煤与型煤最大剪切应变场演化规律Fig.7 Evolution law of maximum shear strain field of raw coal and briquette coal when λ=0.25

图8为λ=0.50时，不同加载时刻原煤与型煤最大剪切应变场云图，该条件下2种煤样应变场局部化带演化规律与λ=0.25时基本相同，荷载作用区与非作用区分界面形成的应力集中区域位于试样中部，与中心孔处于同一截面，最终在此区域形成一条应变局部化带，局部化带方向与加载方向近似平行，试验观测到的试样破坏的主控裂纹也位于此区域。

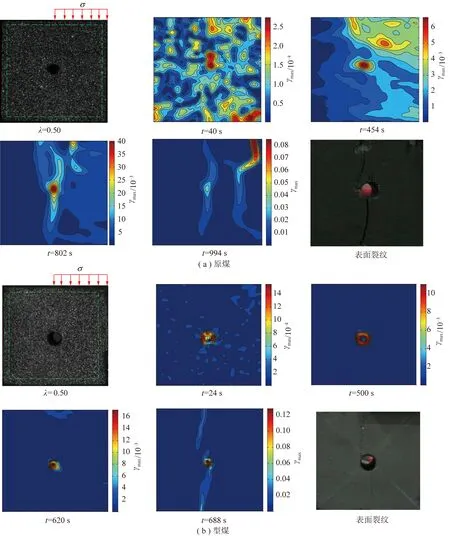
图8 λ=0.50时原煤与型煤最大剪切应变场演化规律Fig.8 Evolution law of maximum shear strain field of raw coal and briquette coal when λ=0.50

图9为λ=0.75时，不同加载时刻原煤与型煤最大剪切应变场云图，该条件下2种煤样应变场局部化带演化规律与加载面积λ=0.25时基本相同，原煤形成的局部化带与加载方向近似平行，型煤试样由于其软塑性特征和非对称荷载程度较高，在未形成明显局部化带前直接受载区即发生大范围破坏；由于中心孔位于非加载区域，原煤试样中心孔周边变形并未出现高应变值集中现象，原煤主控裂纹也未穿过中心孔洞；型煤试样由于其强度太低，对孔的支撑能力较差，孔周边仍出现了较为明显的应变集中现象，这也是该条件下型煤应变局部化带位置与原煤不同的原因，但型煤主控裂纹仍然位于加载区与非加载区交界面区域，并未对中心孔洞造成影响。

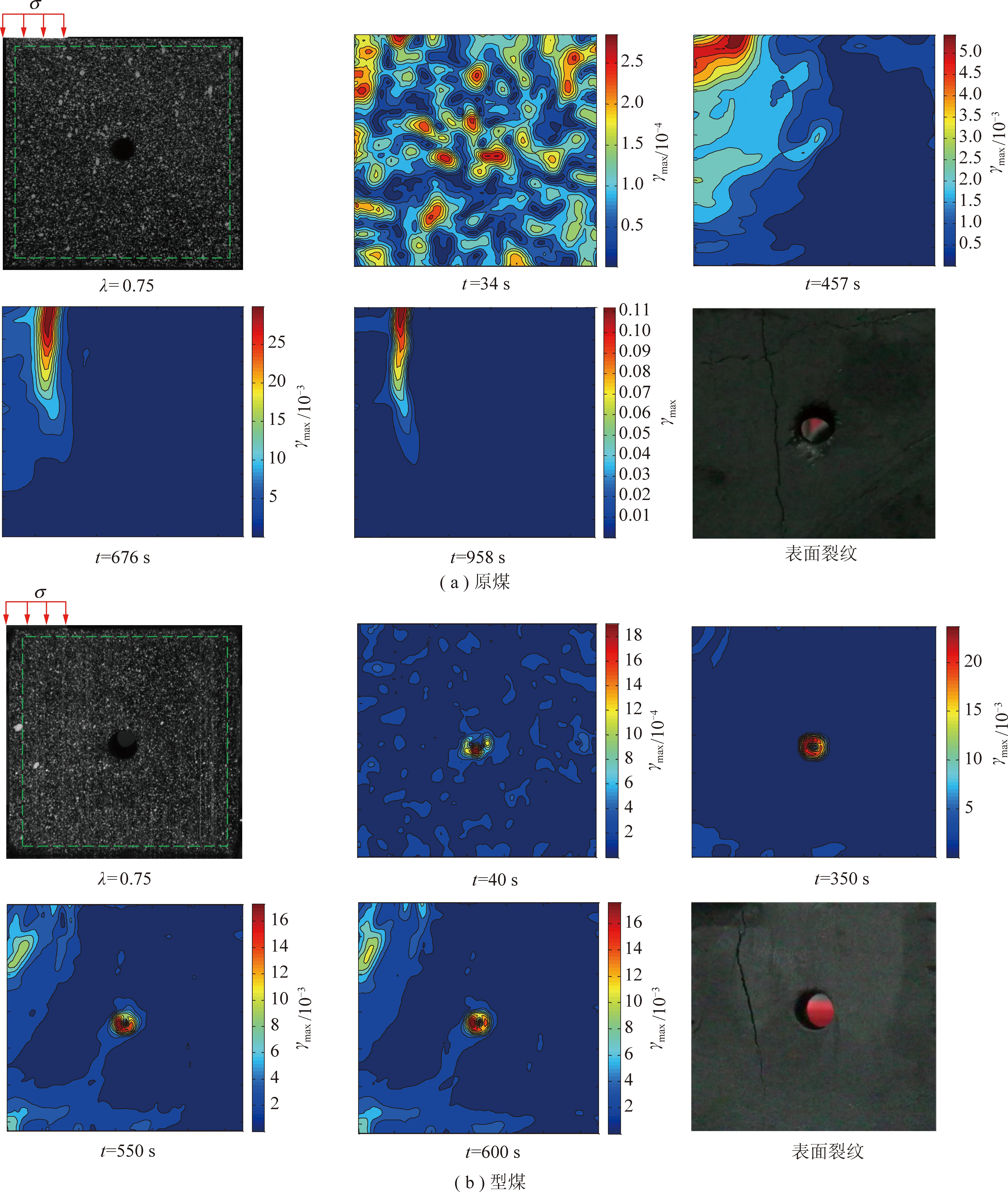
图9 λ=0.75时原煤与型煤最大剪切应变场演化规律Fig. 9 Evolution law of maximum shear strain field of raw coal and briquette coal when λ=0.75

由上述分析可知，均布荷载与非对称作用时含孔原煤与型煤应变场演化均表现出较好的阶段性特征，可分为均匀变形阶段、局部化阶段、破坏阶段；均布荷载作用时原煤与型煤试样宏观破坏模式不同，破坏后形成的局部化带形态不同；非对称荷载作用时，由于加载区与非加载区交界面剪应力作用带的存在使原煤与型煤均发生宏观剪切破坏，煤样主控裂纹与局部化带分布受剪应力作用带与中心孔洞相对位置影响。随着荷载非对称程度的增加，原煤与型煤试样应变场局部化进程加快，局部化带形成所用时间逐渐降低，试样更容易形成局部化带而后发生破坏。煤岩表面应变场演化与裂纹的扩展演化具有较好地对应性，局部化带的形成发展过程能够很好地反映煤岩损伤演化规律。

2.3 局部化演化的定量表征

为了确定应变场局部化带的启动时刻，引入统计指标函数，定量反映应变场局部化演化进程。由最大剪切应变场云图可知，应变局部化带与局部化带外区域相比具有2个明显的特征“数值特征”与“空间特征”[18-19]。

采用应变场各点的标准差反映应变场局部化的“数值特征”，某一加载时刻应变场的标准差Sf可表示为

(3)

式中，n为像素点的数量；Xk为某一时刻第k个点的

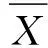
为了反映局部化带的“空间特征”，引入加权函数ws表征局部化带的“空间特征”：

(4)

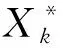
X*=X⊗B

(5)

由卷积的性质可知，应变场的空间集中化程度越大，加权函数ws越大，因此，ws可以表征局部化带的“空间特征”。综合考虑局部化带的“数值特征”与“空间特征”，将定量表征局部化进程的统计指标函数Sw定义为

Sw=(ws+Sf)/2

(6)

统计指标是对应变场演化不均匀程度的反映，当煤岩表面变形出现集中时，应变场不均匀程度增加，统计指标值会增大，对应曲线斜率会发生明显的变化，因此，将统计指标曲线的转折点定义为局部化启动时刻。利用上述公式，借助于Python语言，实现不同加载时刻应变场统计指标值的求解。

为了便于观察，将应力与统计指标进行归一化处理，图10为原煤与型煤在不同非对称系数时应力与统计指标随轴向应变的演化关系曲线(σ为不同加载时刻对应的应力)。

由图10(a)可知，对于原煤试样，λ=0时，在峰值前84.2%σc处，统计指标曲线发生转折，应变场局部化启动，局部化启动应力为39.17 MPa；λ=0.25时，在峰值前95.1%σc处，统计指标曲线发生转折，应变场局部化启动，局部化启动应力为32.98 MPa；λ=0.50时，在峰值前97.8%σc处，统计指标曲线发生转折，应变场局部化启动，局部化启动应力为28.04 MPa；λ=0.75时，在峰值前97.5%σc处，统计指标曲线发生转折，应变场局部化启动，局部化启动应力为16.98 MPa。由图10(b)可知，对于型煤试样，可判定λ=0，0.25，0.50，0.75时应变场局部化启动应力分别为6.48，5.27，3.71，2.56 MPa。

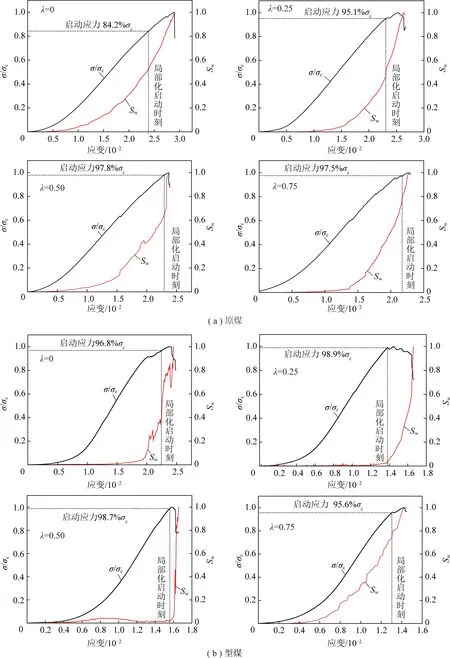
图10 不同非对称系数时原煤与型煤统计指标演化规律Fig. 10 Statistical index evolution law of raw coal and briquette coal with different asymmetric coefficients

通过对原煤与型煤应变场局部化启动时刻分析可知，原煤与型煤应变场局部化启动应力随着非对称系数的增加而逐渐降低，即荷载非对称程度越大，原煤与型煤应变场越容易发生变形集中，形成应变局部化现象。图11给出了原煤与型煤局部化启动应力与非对称系数的关系曲线。由图11可知，随着非对称系数的增加，原煤试样与型煤试样应变局部化启动应力均呈线性函数规律降低。

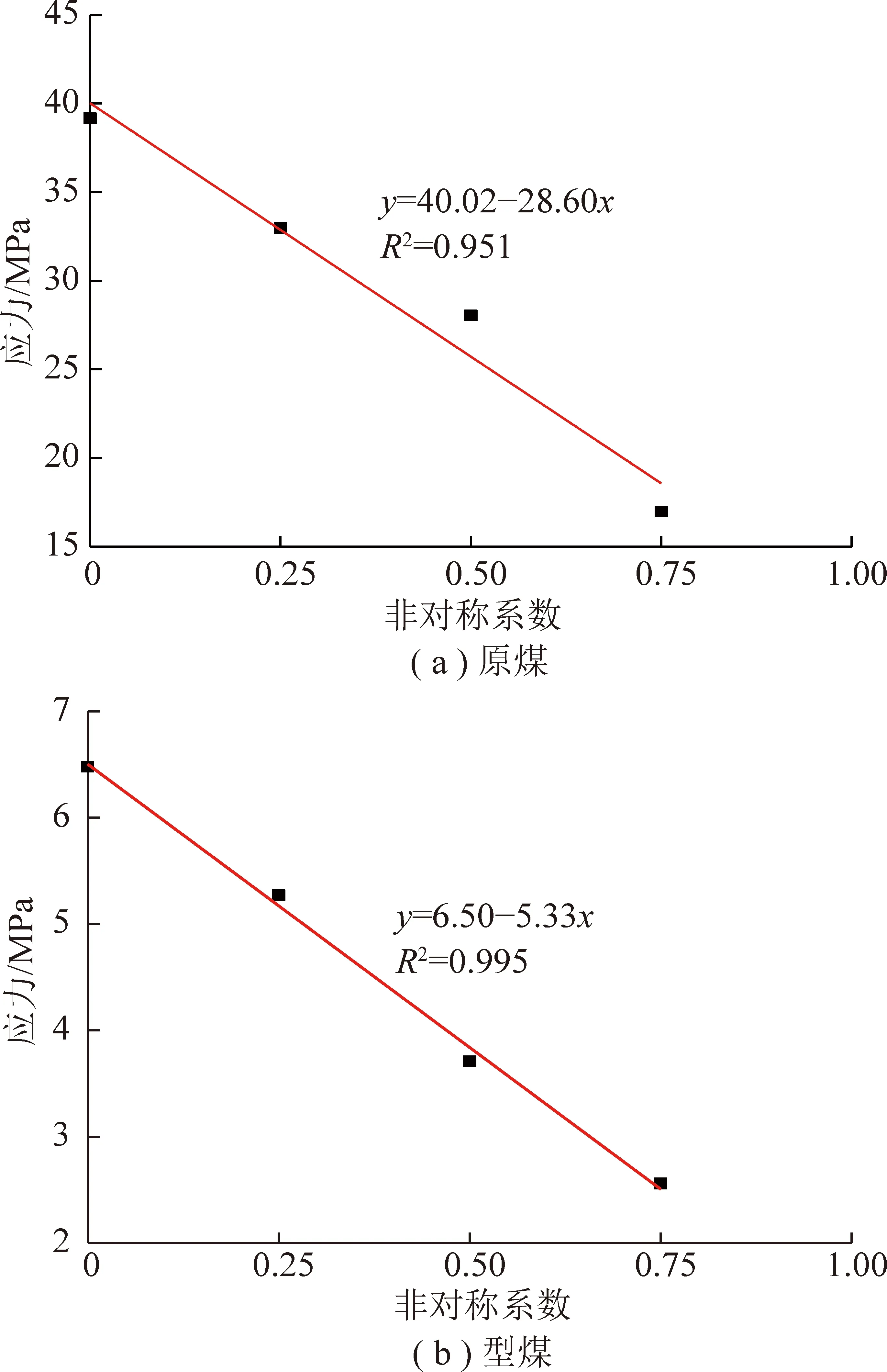
图11 局部化启动应力与非对称系数关系Fig. 11 Relationship between the deformation localization starting stress and the asymmetric coefficient

2.4 损伤本构模型的建立

由上述分析结果可知，最大剪切应变场演化形成局部化带的过程能够很好地反映煤岩的损伤破坏过程，统计指标能够定量反映应变局部化带的形成过程，可用统计指标值表征煤岩损伤情况。因此，用统计指标定义损伤变量Dw即

(7)

式中，Sm为加载过程中统计指标最大值。

以λ=0.50时的原煤与型煤试验数据为例，按式(7)计算了不同加载时刻损伤变量的值，如图12所示。由图12可知，损伤变量与轴向应变关系可用指数函数拟合，即

Dw=κexp(ε1m1)-n1

(8)

式中，κ,m1,n1为模型参数，可通过数据拟合确定；ε1为轴向应变。

假设微观单元体变形满足虎克定律，基于应变等效性假说[20]，可得到描述材料应力应变关系的损伤本构模型，即

σi=Eεi(1-D)+μi(σj+σk)

(9)

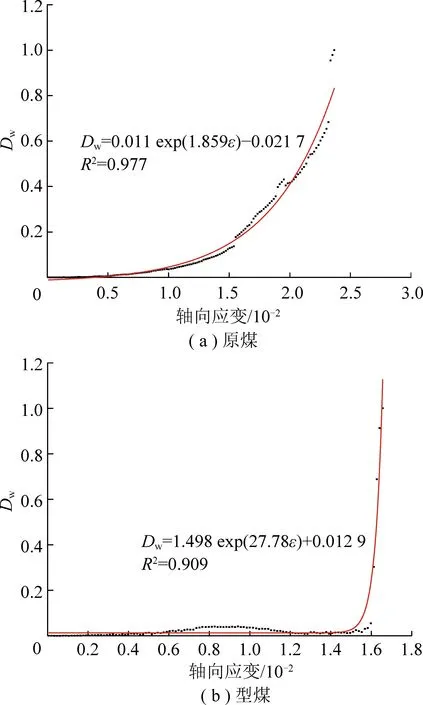
图12 损伤变量拟合结果Fig. 12 Fitting results of Dw

式中，D为损伤变量;σi,σj,σk为材料未受损部分在i,j,k方向的宏观名义应力；εi为名义应力σi作用下产生的应变；E为材料弹性模量;μi为材料在i方向的泊松比，(i,j,k)=(1,2,3),(2,3,1),(3,1,2)。

将式(8)代入式(9)中即可得到基于统计指标定义的材料损伤本构模型，即

σi=Eεi[1-κexp(m1εi)+n1]+μi(σj+σk)

(10)

式(10)是基于材料在受载前未发生损伤建立的，而煤岩材料内部包含丰富的孔隙、裂隙结构，中心孔洞亦可看做是煤岩材料的原生孔隙，式(10)所得的应力应变曲线不能反映煤岩材料受载初期的压密阶段。有效介质理论认为岩石是由基质与裂纹组成的各向异性材料[21]，岩石受载后产生的应变可分为基质压缩产生的应变与裂纹状态变化产生的应变。单轴压缩条件下初始压密阶段轴向应变可表示为

(11)

式中，σ1为轴向应力；a为压密阶段裂隙闭合产生的最大应变；b为模型参数；a,b可通过参数拟合求得。

联立式(10),(11)，可得到一种单轴压缩下考虑初始损伤的煤岩本构模型，该模型采用分段函数表示，具体为

(12)

式中，εc为岩石裂纹的闭合应变，为应力应变曲线弹性阶段反向延长线与应变轴的交点；ε0为两曲线的交点。

利用前文中原煤与型煤试验数据验证本文建立的损伤本构模型的合理性。图13给出了试验所得原煤与型煤的应力应变曲线与理论计算得到的应力应变曲线的对比结果，理论计算过程中模型参数取值见表1。

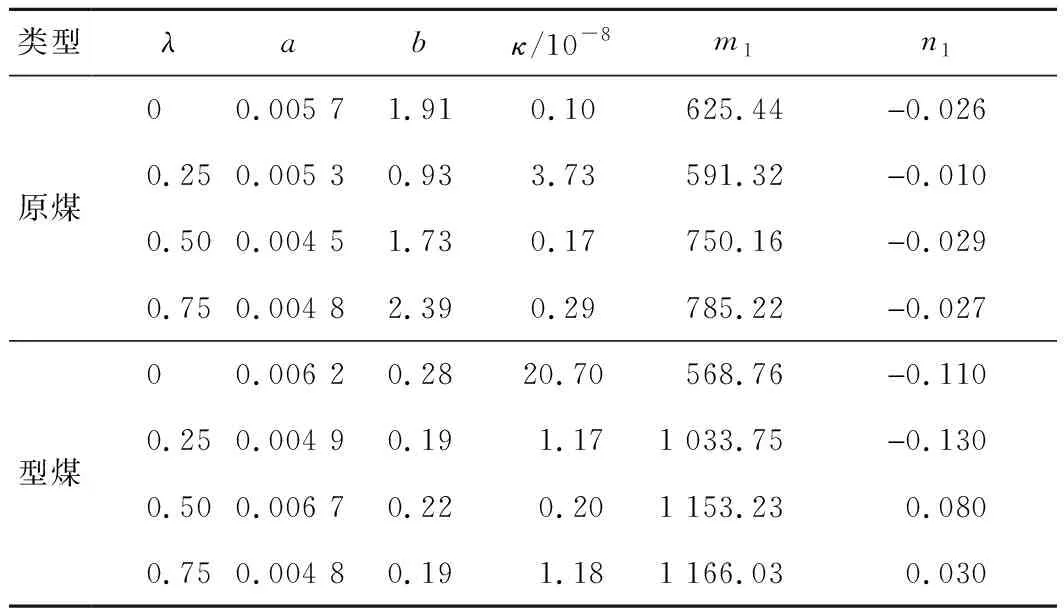
表1 非对称荷载本构模型参数取值

由图13可知，基于统计指标建立的损伤本构模型的理论曲线与试验曲线吻合较好，能够反映原煤与型煤应力应变曲线各阶段的特征，表明本文建立的损伤本构模型的合理性。

3 讨 论

应变场演化规律分析结果表明非对称荷载下煤岩应变局部化受到非对称荷载程度、非对称荷载与中心孔洞相对位置等共同影响。WANG等[22]开展了不同非对称程度荷载作用下完整煤样应变场局部化演化规律研究，为了分析中心孔洞与荷载非对称程度对煤样变形局部化的影响，引用WANG等的部分试验结果与本文试验结果进行对比分析。图14为不同λ时含孔与完整煤样破坏时刻最大剪切应变场云图。

由图14(a)可知，λ=0.25时，完整煤样应变场局部化带均处于加载区与非加载区之间的剪应力集中带附近，试样最终破断面也位于该区域内部；当煤样中含有中心孔洞时，此时中心孔洞处于加载区范围内，煤样应变场局部化带均向中心孔洞发生偏移，局部化带均穿过中心孔洞。由图7也可以看出，表面裂纹由加载板端部的应力集中位置起裂，沿剪应力集中带向下扩展过程中向中心孔洞位置发生偏转，穿过中心孔洞后继续扩展至试样破坏。因此，该加载条件时中心孔洞对煤样损伤破坏起到引导作用。

图14(b)为λ=0.50时含孔与完整煤样破坏时刻最大剪切应变场云图，由图14(b)可知，λ=0.50时，中心孔洞位于加载区与非加载区之间，此时中心孔洞的存在对应变场局部化带形状影响不大，完整煤样与含孔煤样局部化带均大致位于加载区与非加载区间剪应力集中区域。

图14(c)为λ=0.75时含孔与完整煤样破坏时刻应变场云图，由图14(c)可知，λ=0.75时，完整煤样破坏时刻应变场局部化带均位于加载区与非加载区之间剪应力集中区域。中心孔洞位于非加载区范围内，中心孔洞对煤样应变局部化带位置影响不大，对于原煤试样，由于其硬脆性特征，中心孔洞周边变形不大，仅在加载区与非加载之间形成了应变局部化带，中心孔洞对应变场局部化效应的影响可以忽略；对于型煤试样，由于其软塑性特征，剪应力集中带的存在会对中心孔洞产生影响，孔周边会产生一定变形，但应变主要变化区仍集中在加载区。由图9中裂纹分布也可看出，该条件下裂纹仅分布于加载区与非加载区交界面区域，裂纹扩展并未向中心孔洞位置偏转。

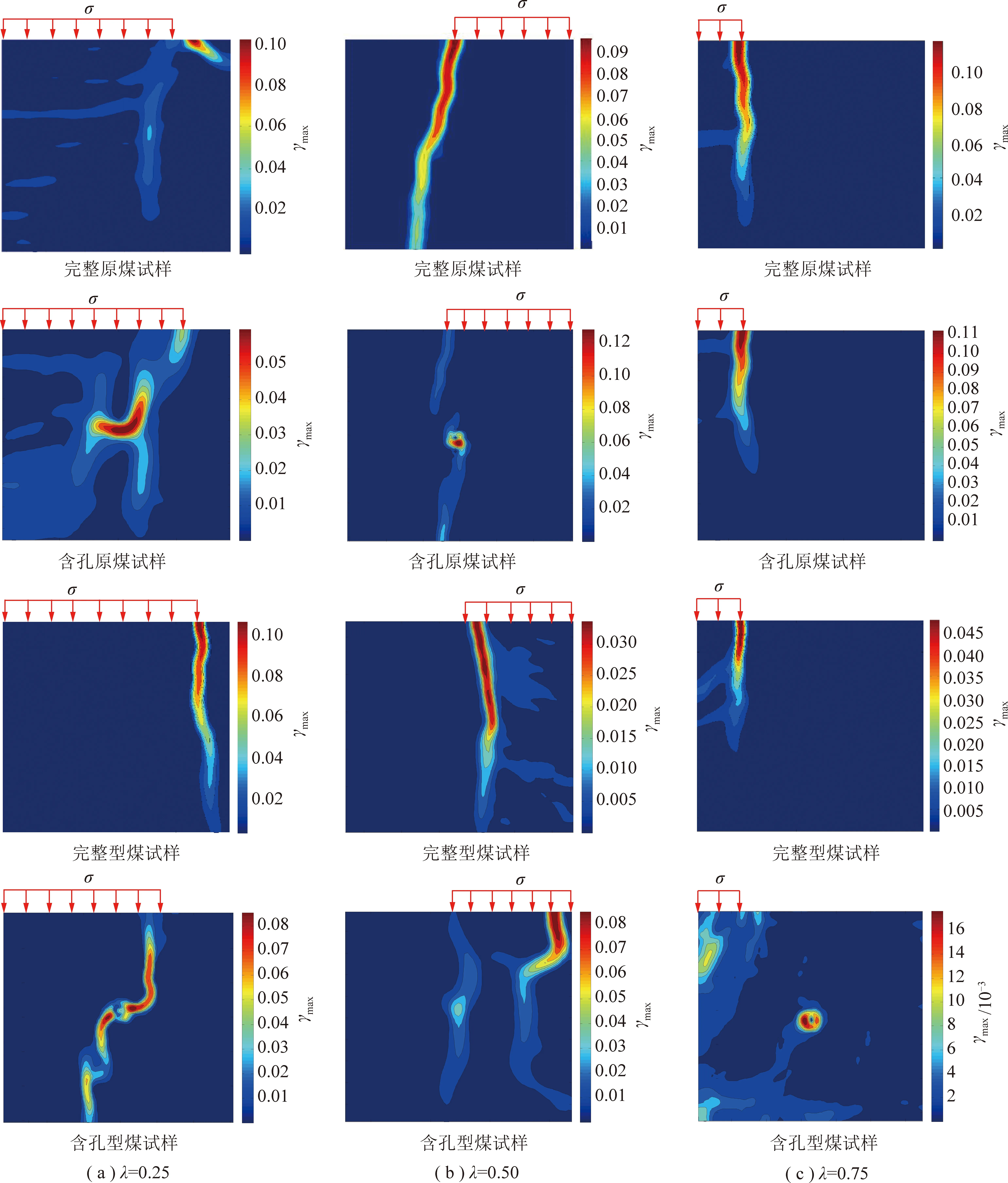
图14 不同非对称系数时煤样最大剪切应变场云图Fig.14 Cloud chart of maximum shear strain field of coal samples with different asymmetric coefficients

由上述分析可知，非对称荷载作用时原煤与型煤变形局部化带与表面裂纹分布受加载区与中心孔洞的相对位置影响，当中心孔洞处于加载区时，变形局部化带与表面裂纹演化方向受加载区与非加载区之间的剪应力带与中心孔洞共同影响，形成的变形局部化带与表面裂纹处于连接加载板端部与中心孔洞位置；当中心孔洞处于非加载区时，变形局部化带与表面裂纹演化方向主要受加载区与非加载区之间的剪应力带位置影响，形成的变形局部化带与表面裂纹位于剪应力带附近，中心孔洞对二者形态的影响程度取决于煤岩的强度，煤岩强度越大，中心孔洞对二者形态影响越小。

4 结 论

(1)原煤与型煤峰值应力均随着荷载非对称系数的增加呈线性函数规律减小；加载区与非加载区交界面剪应力作用带的存在是原煤与型煤发生宏观剪切破坏的主要原因。

(2)非对称荷载作用下含孔原煤与型煤应变场演化均包含均匀变形阶段、局部化阶段、破坏阶段；加载初期，原煤高应变值全场分布，而型煤试样高应变值主要集在中心孔洞附近。

(3)定义了可定量表征煤岩表面应变场局部化程度的统计指标函数，确定了原煤与型煤不同受载条件下的局部化启动应力，发现原煤与型煤试样局部化启动应力随着荷载非对称程度的增加均逐渐降低，表现为线性函数规律。

(4)变形局部化带与表面裂纹分布受加载区与中心孔洞的相对位置影响，当中心孔洞处于加载区范围时，2者从中心孔洞穿过；当中心孔洞处于非加载区时，中心孔洞对2者形态的影响程度取决于煤岩的强度，煤岩强度越大，中心孔洞对二者形态影响越小。

(5)基于统计指标函数定义了表征煤岩损伤的损伤变量，建立了可反映整个加载阶段的煤岩应力应变特性的损伤本构模型，借助于试验数据验证了所建模型的合理性。