上吸式固定床生物质气化炉氧化层和还原层设计的热态数值模拟

严文记 胡翠娟 黄波荣

（佛山蓝之鲸科技有限公司，佛山 528225）

在生物质气化炉的设计中，氧化层和还原层的设计在整个气化过程中起着关键作用，尤其是高度设计是否合理直接决定了气化效率的高低。为了更详细地了解不同还原层在不同高度下运行的基本特性，采用计算流体动力学（Computational Fluid Dynamics，CFD）方法对气化炉氧化层和还原层内的氧气和二氧化碳浓度分布情况进行数值计算，获得不同工况下二氧化碳浓度随还原层高度变化的规律，为生物质气化炉的优化设计提供理论依据。

1 模拟工况的确定

在进行计算机数值模拟计算时，气化炉的炉型结构确定后，影响气化炉内工质运行状态的主要是燃料颗粒度大小和氧化层与还原层的高度[1-2]。本文热态模拟将根据以往的设计经验取燃料直径为100 mm、120 mm、140 mm、160 mm和180 mm这5个长度进行模拟计算。在进行数值模拟计算工作前，先建立氧化层和还原层的几何模型。

2 几何模型的建立

氧化层和还原层数值模拟的几何模型采用真实的燃料颗粒尺寸（直径分别为100 mm、120 mm、140 mm、160 mm和180 mm），并作简化处理。首先，模型的壁面与环境没有热量交换，壁面为绝热壁面。其次，模型内为不可压缩流体，因此密度不会改变。再次，模型内的物料处于动态平衡。最后，模型的物理参数不随时间变化，即为稳态过程。通过以上假设，利用UG12.0三维软件建立三维模型，如图1所示。

图1 几何模型

3 还原层网格划分和网格无关解验证

网格划分时，首先在UG12.0中建立好几何模型，以STP的格式输出文件，导入到CFD前处理器geometry中进行表面处理，再导入mesh中划分网格。为了增强计算的精确度，需要在几何表面临近计算区域的距离向内缩短，再靠近壁面区域划分精密的网格，并在内部流体区生成与表面网格组合的四面体网格[3]。划分网格需要进行网格无关解验证，分别建立网格数量为100万、200万、300万、400万、500万以及600万。网格无关解验证点（如图2所示的点）取在氧化层出口的截面上，其二氧化碳浓度随网格数量的变化情况如图3所示。可以看出当网格数量从400万个增加到600万个时，参考点的二氧化碳的浓度在15%左右，基本不发生变化。为了节约时间，取网格数量在400万个时进行氧化层的模拟计算。

图2 氧化层网格划分图

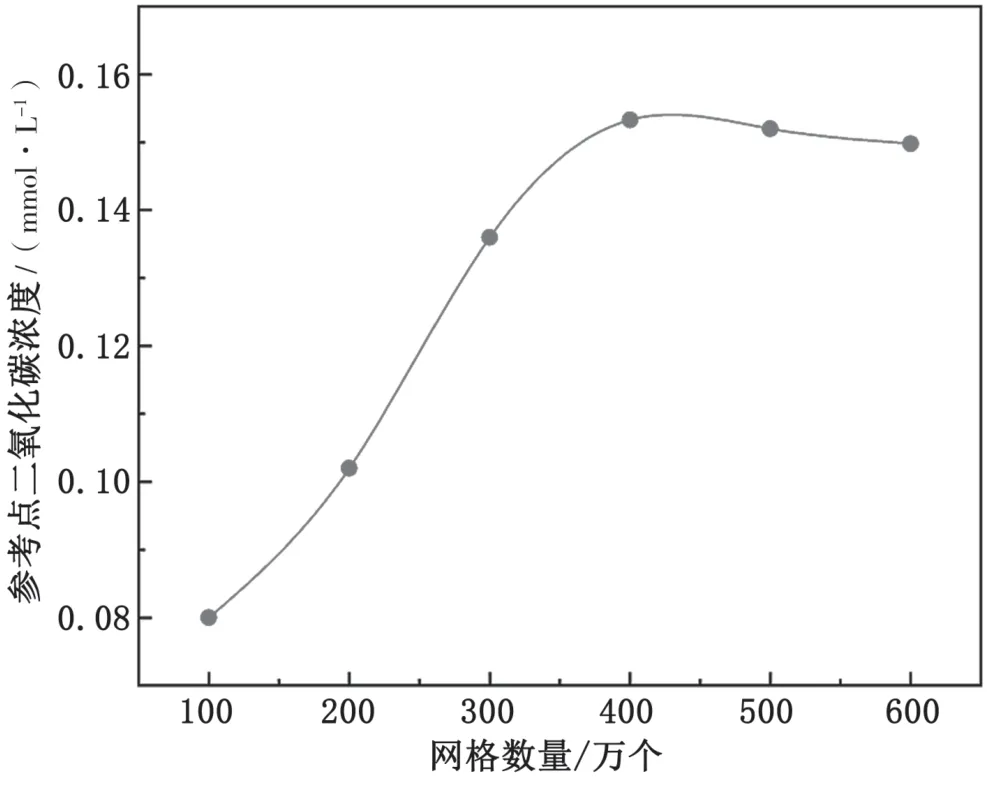
图3 二氧化碳浓度随网格数量的变化

4 边界条件

为了能最大限度地满足实际工程，要选用能够对计算结果的准确性有保障的fluent模型的边界条件。本文中边界条件均根据实验和经验给定。

4.1 入口边界条件

在还原层模型的下方面设气化剂入口面为inlet-air，速度值根据通风量为6 000 m3·h-1计算为8 m·s-1，气化剂中浓度氧气设为0.22 mmol/L，其余为氮气，并设为恒定速度边界面。假设氧化层内气流为完全湍流，气流方向沿验轴线向上，模型中圆柱形颗粒设为生物质颗粒与气化剂接触面。

4.2 出口边界条件

由于氧化层的出口是还原层的进口，可将氧化层出口面气流参数设为还原层进口参数[4]。所以，在氧化层模型上方面设为outlet出口边界条件。

4.3 壁面边界条件

实际工程应用中，炉内气化的速率相对较快，因此氧化层模型需要采纳k-ε模型[5]。因为它的高雷诺数较高，壁面处湍动能和湍流耗散率都设置为0，设为绝热边界条件。边界条件的具体数值见表1。

表1 边界条件

5 氧化层和还原层高度随粒径变化规律的模拟结果

由于气化炉的气化过程较为复杂，按照提到的方法简化模型，计算燃料粒径分别为100 mm、120 mm、140 mm、160 mm和180 mm时氧气、二氧化碳和一氧化碳浓度分布。通过气体分布值确定反应层高度，原则主要有两个方面：一是氧气浓度为零的位置即氧化层所需要的高度；二是二氧化碳浓度为零的位置即还原层所需要的高度[6]。具体计算结果如图4～图13所示。

图4 100 mm粒径氧化层O2浓度分布

图13 180 mm粒径还原层CO2浓度分布

图5 100 mm粒径还原层CO2浓度分布

图6 120 mm粒径氧化层O2浓度分布

图7 120 mm粒径还原层CO2浓度分布

图8 140 mm粒径氧化层O2浓度分布

图9 140 mm粒径还原层CO2浓度分布

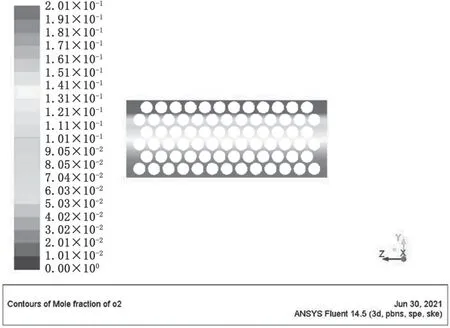
图10 160 mm粒径氧化层O2浓度分布

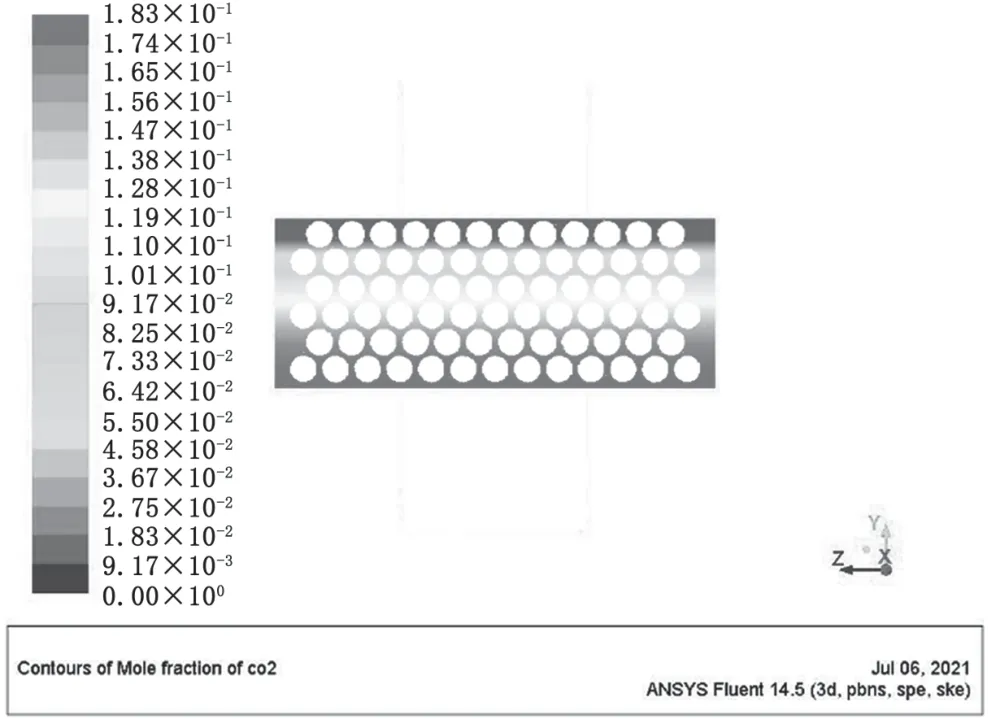
图11 160 mm粒径还原层CO2浓度分布

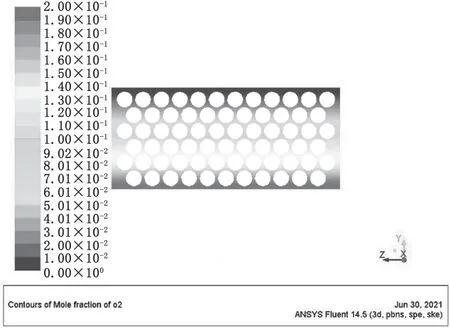
图12 180 mm粒径氧化层O2浓度分布

从以上5种不同粒径的生物质燃料的热态数值模拟结果来看，不同粒径的燃料所需的氧化层和还原层高度相差较大。这对气化炉结构优化的影响较大，有必要进行详细研究。不同粒径的生物质燃料气化所需的氧化层和还原层高度，见图14。

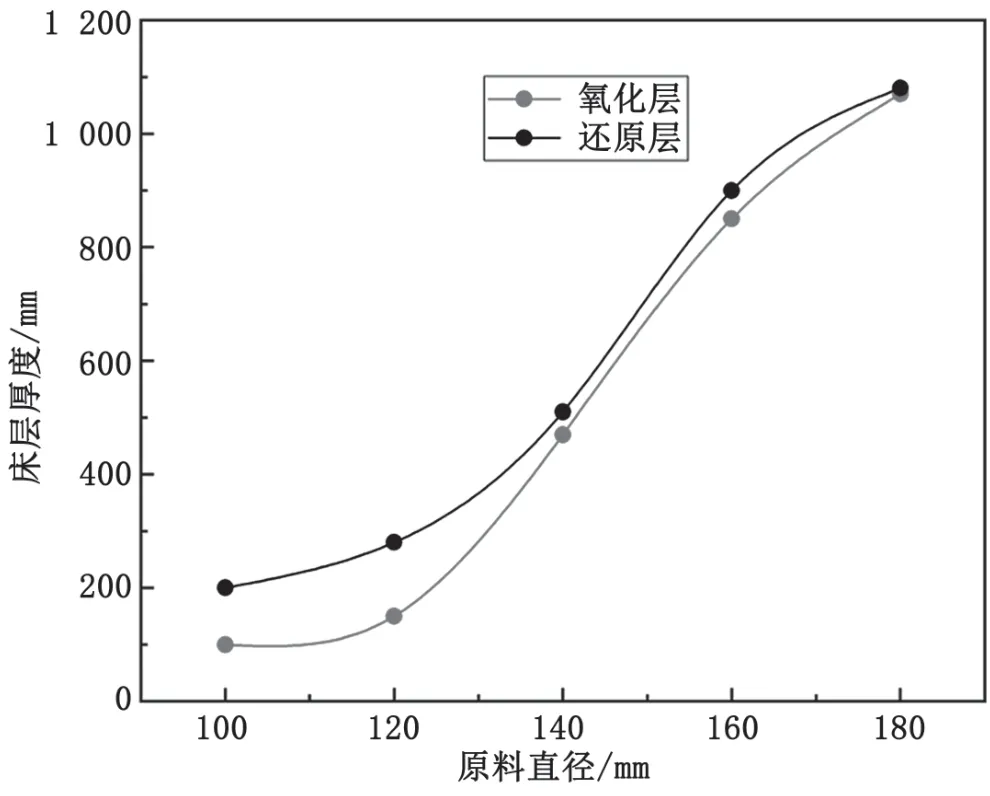
图14 床层厚度随燃料粒径变化图

由图14可知，还原层的高度高于氧化层的高度，这与实际设计经验相符合。床层厚度随着生物质燃料的粒径增大先缓慢增大，当粒径增加到140 mm时，床层厚度随粒径的增加迅速增加，说明当燃料粒径小于140 mm时炉内的燃料颗粒堆积比较密集，粒径大于140 mm燃料颗粒堆积比较稀疏。燃料在气化炉内堆积过于密集，空隙太小造成气流阻力过大，相应增加了电耗，且燃料层厚度太薄，顶部上料时不利于控制[7]。燃料堆积过于稀疏时将会增加床层高度，需要设计更高的气化炉，会增加气化炉的造价成本[8]。因此，生物质气化炉运行时生物质燃料破碎后粒径取140 mm左右为宜，因为燃料的粒径取140 mm时阻力较低，且氧化层和还原层的高度相差不大，都为

500 mm。

6 结论

本文建立了生物质气化炉氧化层和还原层的几何模型，根据气化炉燃烧的理论知识建立燃烧计算模型，进行数值模拟的网格无关解验证，计算获得了不同燃料粒径下气体浓度的分布规律，得出以下结论：

（1）建立的数学模型是合理的；

（2）生物质原料破碎后粒径取140 mm左右为宜；

（3）氧化层和还原层高度均取500 mm为宜，与现有的上吸式固定床生物质气化炉（氧化层高度1 m，还原层高度1 m）相比，氧化层和还原层高度均降低500 mm，整个气化炉高度降低1 m，证明数值模拟的结果是合理的，可以为生物质气化炉的优化设计提供理论依据。