基于超声波渡越时间的非稳态温度场数值计算与实验研究

田雨生,刘东尧

(南京理工大学 能源与动力工程学院，南京 210094)

1 引言

金属材料的高温瞬态热冲击是兵器科学与技术领域的重要问题之一。在火炮发射过程中，火药燃烧后会迅速将化学能转化为热能并传递给身管。火药燃气可以达到2500～3500 K的高温[1]，而身管内壁也会在毫秒内达到1 000 K以上的高温，不管是接触测温还是非接触测温，都面临温度高、变化快、压力大、电磁干扰、高冲击波等恶劣的条件。

在传统方法中，获得温度场内部温度时需借助于内置的温度传感器，这样不仅影响温度场内部的流动状态，也使得传感器易于受环境的干扰而影响测量数据的准确性[2-4]。超声波测温是一种新的测温技术,由于它是非接触式测量[5],故可用于火箭排气、汽缸燃烧气体、熔融液、核反应堆石墨芯等处的测温。近年来研究者们提出多种超声测温技术，如SEI公司将研制的Biolerwatch系列声学温度计用于测量大型火力发电厂中锅炉内部温度场的分布情况[6]，测量范围 300～2 700 ℃，1 200 ℃以上的误差不大于2 ℃，这代表着超声温度计已经从实验室逐步走入产品化阶段[7]。英国的 CODEL 公司成功研制出测量大型烟气管道温度的声学测温装置，实现了气体温度的实时测量[8]。2003年，华中科技大学成功研制了用来测量超声波在炉膛内传播渡越时间的硬件系统[9]。2007年，华北电力大学的沈国清提出了时间延迟算法，是测量超声波渡越时间的一种新的计算方法[10]，并通过大量的实验，验证了该算法能有效地抑制噪声[11]。2008年，沈阳工业大学的颜华等提出了互相关和插值运算的方法，提高了超声波对待测温场温度测量的精度[12]。2009 年，Kobayashi等成功研制出了耐高温换能器，实现了对高温环境下温度的精确测量[13]。此外，东北大学的邵富群教授研发团队，从声源信号的产生、声音信号的降噪、温度场重建算法以及测温实验系统构成进行了大量的研究和实验，为超声测温技术发展提供了数据支持和理论依据[14]。同时，成功设计了一套实验室使用的声学测温系统[15]。

上述的超声测温系统主要针对稳态或准稳态温度场的测量。而火炮身管在发射过程中温度变化的非常剧烈，是一个典型的瞬态温度场测量问题。本文利用超声波在金属材料中的传播速度会随着材料的温度而变化这一特点，测得材料一段连续时间内的超声波渡越时间参数(time of flight,TOF)，用超声波CT图像与导热方程，求出空间中各点温度分布和变化，重建温度场。

2 温度场重建原理

对圆柱型金属材料一端通过火焰进行加热，另一端置于常温中，则该圆柱体热传导问题可简化为沿轴向的一维无内热源非稳态导热问题。此类问题在已知加热端与常温端温度的情况下，便构成了第一类边界条件下非稳态导热的定解问题。

2.1 一维非稳态导热问题的数值求解

一维无内热源常物性的非稳态导热微分表达式为：

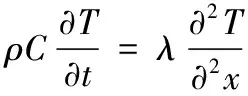
(1)

其中:ρ为材料密度；C为比热容；λ为导热系数；T为温度；t为时间；x为长度。对于一维非稳态导热问题，将材料按导热方向将划分为M个点，将加热过程按经过的时间划分为N个点，则可得到共M·N个网格点，对方程(1)中左端非稳态项在网格点(m，n)处进行向前差分，可得：

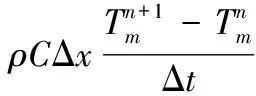
(2)

同样，对方程式(1)右端扩散项进行Taylor级数展开，可得网格点(m+1,n)处温度：

(3)

同理，网格点(m-1,n)处温度：

(4)

将两式相加得到扩散项在网格点(m,n)处二阶差分形式为：

(5)

故其离散方程为：

(6)

引入Fourier数与热扩散系数后整理得：

(7)

2.2 超声波渡越时间与材料温度关系

超声波纵波在金属材料中传播速度与弹性模量关系为

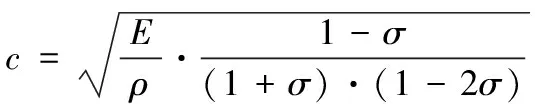
(8)

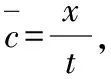
(9)

由式(9)可知，对于金属材料某网格点，在已知其网格长度、材料密度、泊松比时，即可通过超声波在该网格处渡越时间求出弹性模量。而材料的弹性模量是一个与温度有关的参数，故可以通过查表法根据弹性模量求出该网格处平均温度。

2.3 利用渡越时间求解非稳态温度场原理

超声波渡越时间与路径上材料的温度平均值相关，直接测量的渡越时间并不能确定路径上的温度场分布，需结合非稳态温场的数值求解确定。在瞬态热冲击作用下，受热面温度快速上升，然而冷端温度基本不变，可以采用直接测量方式给出；待测热端传热过程非常复杂，火焰和材料端面之间存在着对流、辐射和传导3种传热效应，对于这种瞬态的复杂传热过程，理论和实践上都难以定量地给出边界条件。本文对热端温度计算的方法如下：通过不断检测连续发射和反射的脉冲超声波渡越时间，扫描加热端温度的变化，在加热过程未发生之前，各列脉冲超声波的时差相同，各网格点温度相同；一旦开始加热，材料加热端端面温度将首先开始变化，测量得到的脉冲超声波渡越时间就会相应的发生变化。渡越时间的变化是由两部分引起的：火焰对端面的传热与上一时刻到此时刻为止材料内部的导热。其中火焰对端面的传热占据主要因素。求解时，首先假设除端面网格点外，其他网格点温度不发生改变，则可以通过渡越时间差确定该时刻加热端面上网格点的温度值，并将其作为加热端面上的边界条件，通过导热方程求出其余网格点温度。并在此假设条件下计算除端面网格点外的总渡越时间。将实际渡越时间与除端面网格外的总渡越时间相减，即可求出修正后的端面网格点温度。反复迭代此过程直至计算得出的所有网格点温度对应渡越时间之和与实际总渡越时间误差在给定范围之内。此时求出的温度场即为考虑了端面传热与内部导热2个影响因素的数值解。上述过程可以总结如下：

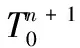
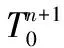
5) 重复过程3)直到理论渡越时间与实际渡越时间误差小于给定误差；

5) 在非稳态传热过程结束之前，检测到下一次脉冲超声波时差，转到过程2)；

6) 结束计算。

3 金属材料测温实验过程及结果

3.1 实验条件

实验内容为采用丁烷喷灯火焰加热长圆柱体金属材料一端。另一端连接超声波收发一体探头。通过超声脉冲发生器以固定频率发射超声波，并在接收到反射后的回波时通过示波器显示波形图像，并用高速摄像机记录波图像变化过程。同时对材料固定点使用热电偶测温，用于验证实验结果。随后通过图像识别软件将波形图读取为超声波渡越时间。最终利用计算机重建材料温度场。

实验所用金属材料为镍基合金Inconel 601，其各项参数与温度关系如表1所示。

表1 材料参数

在计算过程中，通过插值法给出不同温度下材料各参数。

待测金属材料为长度330 mm，直径45 mm的实心长圆柱体，为了验证温度场正确性，在材料两端与中部对称地加工出6个盲孔以放置热电偶，如图1所示。需注意的是两端测量点距离端面的距离为1.5 mm。

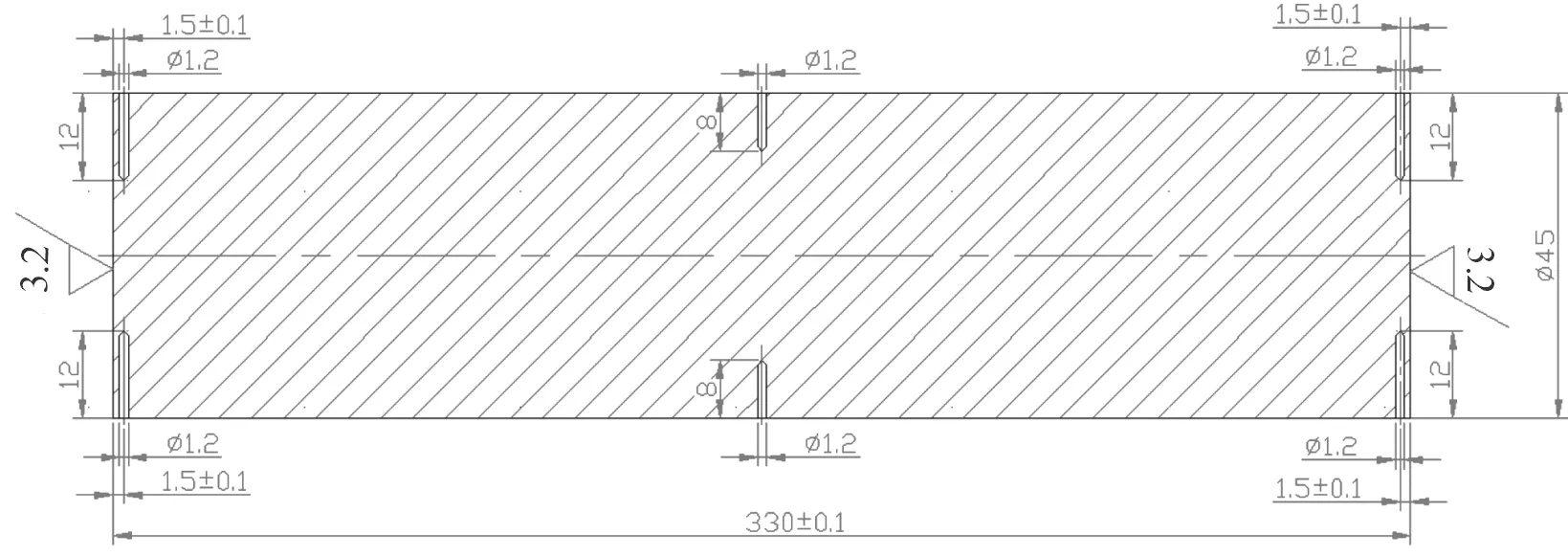
图1 圆柱体加工图Fig.1 Material drawing

实验所用超声波发生器型号为CTS-8077PR脉冲发生器，重复频率采用100 Hz。示波器型号为GDS-3252型数字存储示波器。高速摄像机拍摄频率采用250 Hz。

3.2 超声波波形图像

当示波器时标网格单位为10 ms时，测量得到的超声波图像如图2所示。此时每个脉冲就是一次超声波发射和回波信号，每个脉冲之间间隔为10 ms，即100 Hz重复频率。

当示波器时标网格单位为20 μs时，每个脉冲的波形图像如图3所示。其中最左侧靠近时标零点的波形为发射波，经历约5.6个时标网格后，接收到第一次反射波。两波形之间的时间间隔即为渡越时间。

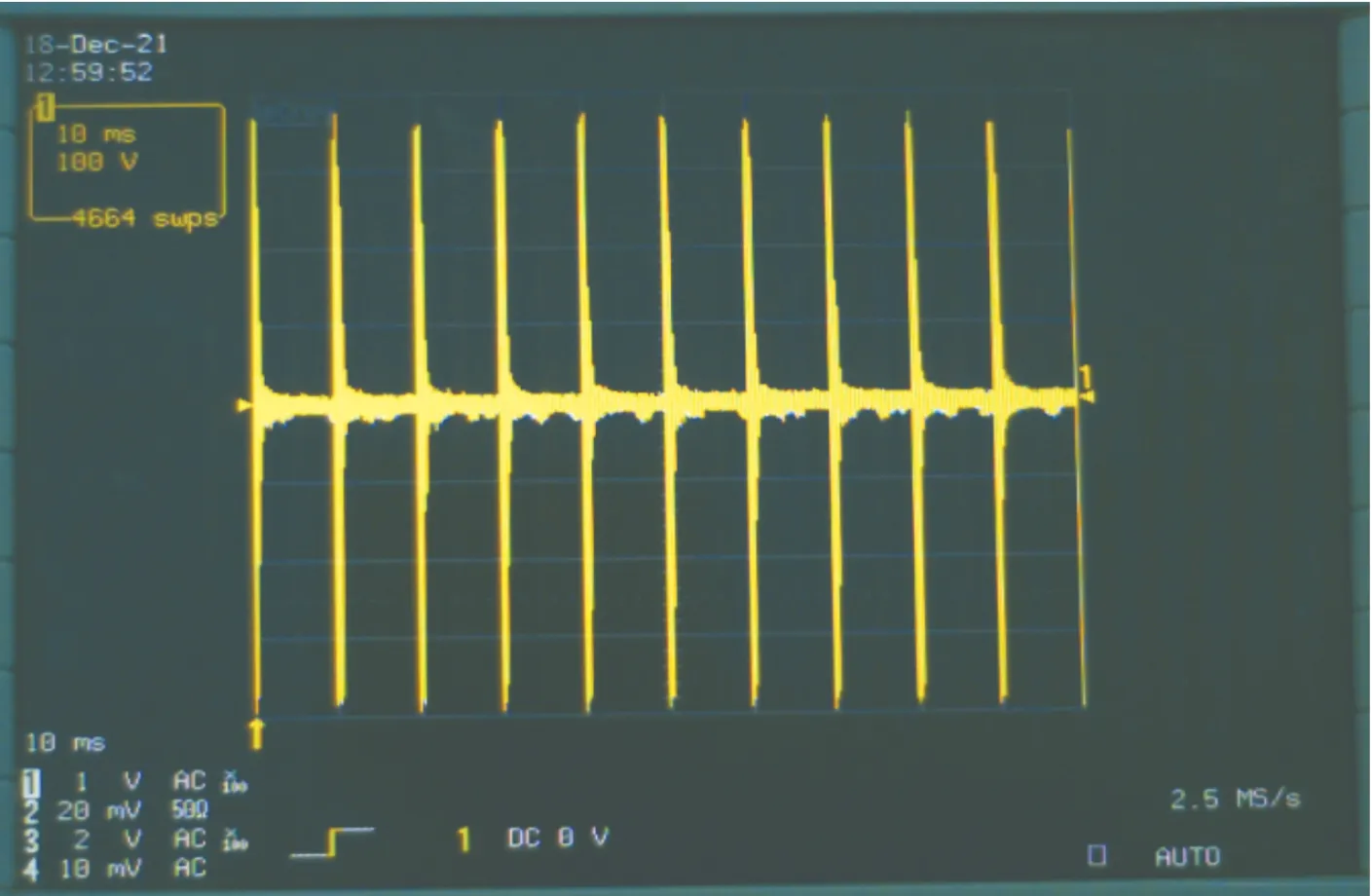
图2 网格点为10 ms波形图像Fig.2 Waveform diagram with grid point of 10 ms

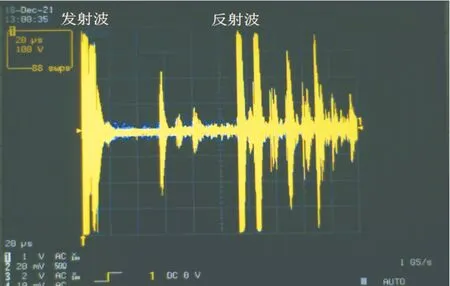
图3 网格点为20 μs波形图像Fig.3 Waveform diagram with grid point of 20 μs

由于金属材料中超声波传播速度较高，材料温度变化时，超声波一次反射的渡越时间变化较小。为了提高测时精度，提高时标网格的分辨率到20 ns，并将图3中第一次反射波的过零点与时标零点对齐，将回波与X轴交点视为触发点，则初始渡越时间为113.150 μs，如图4所示。

图4 网格点为20 ns波形图像Fig.4 Waveform diagram with grid point of 20 ns

金属材料受热端一旦受到丁烷火焰的加热作用，由于温度的升高导致超声波传播速度的降低，对应的渡越时间将增大。在图4中所显示的回波脉冲将向右移动。通过高速录像可以记录到随着热端温度迅速及热量的传递，回波信号移动序列图像。受丁烷火焰温度及材料传热性能的限制，当观测到热端温度变化不明显时，即停止实验，加热过程持续约100 s。

3.3 温度场重建

在超声波回波图像的记录过程中，高速摄像机共采集到19 965张有效图像。图5为距离材料受热面1.5 mm处测温点的温度随时间变化关系曲线。其中实线为通过渡越时间计算出的温度，虚线为安装在该处热电偶测得的温度。由图可见，在材料受热端，计算得出的温度与热电偶所测得温度基本一致。其平均相对误差为3.53%。最大相对误差为15.59%，另外，整个过程中加热端最大绝对误差为5.04 ℃。

图5 加热端温度变化Fig.5 Temperature change at the heating end

加热结束时，沿热量传递方向上的温度分布的计算结果如图6所示。由于实验采用的Inconel 601材料其导热系数较低、热容量较大，在整个加热过程中，材料内部热惯性大、热量传递比较缓慢，故材料中部与常温端温度几乎没有变化。

图6 加热结束时材料温度分布的计算结果曲线Fig.6 Material temperature distribution

金属材料在整个加热过程中温度场变化如图7所示。其中距离表示材料上任一点到加热端的距离。在整个加热过程中，受热面温度快速上升，在受热面附近的温度变化较为明显，且距离受热面越近，温度上升越高。在受热面的表面，其最高温度为176.5 ℃。但是离开受热面一定距离，温度基本保持不变。这与图4所描述的温度分布规律基本一致。

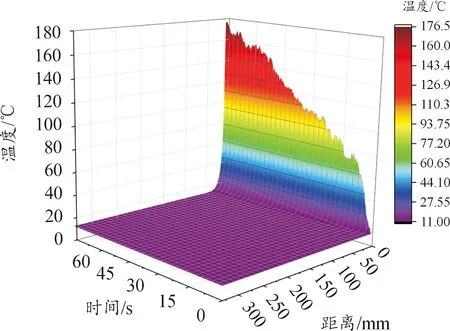
图7 材料温度场变化图Fig.7 Material temperature field change

4 结论

以瞬态热冲击作用下，金属材料的温度场的非接触测量为工程背景，研究了火焰热流作用下金属材料温度变化规律，设计了一种利用超声波渡越时间求解金属材料非稳态传热时温度场变化的计算方法。初步得到如下结论：

1) 以镍基合金Inconel 601材料进行热流冲击加热实验和计算，计算了其在一端受热时温度分布情况，并与热电偶测温结果进行了对比与误差分析。

2) 本文所设计超声波测温方法可适用于温度场变化情况复杂的非稳态导热环境，解决了传统超声波测温对环境温度的稳态或准稳态要求问题。

3) 为金属材料的非接触式测温提供了一种行之有效的方法，较传统热电偶测温等方法，这种非接触式测温方法无需置于待测对象温度场内部，不会受对象内部恶劣环境干扰，且对温度场的变化几乎不会产生影响，为通过超声波测温方法对火炮发射时身管温度场的求解奠定了基础。