变形仿生飞翼跨介质无人机外形设计与航行仿真

吕 达,苏浩秦，2,李 筠,张子俊, 龙 浩，马 宇，刘晓伟

(1.中国航天空气动力技术研究院， 北京 100074；2.彩虹无人机科技有限公司， 北京 100074； 3.北京联合大学 北京市信息服务工程重点实验室， 北京 100101； 4.北京联合大学机器人学院， 北京 100027)

1 引言

水空两栖跨介质无人机是一种同时拥有水中、空中运动能力的无人机，且其能通过自身能量及驱动装置多次跨越水、空两种介质。水空跨介质无人机具备了水下航行器的隐蔽性以及空中无人机的机动性，能同时完成水中及空中的作业及作战任务，得到了各国研究人员的广泛关注，是无人系统装备发展的研究热点。现有的跨介质无人机主要可分为仿生滑翔跨介质无人机、变形跨介质无人机、多旋翼跨介质无人机、仿生扑翼跨介质无人机等。目前，已经取得实质进展或实现跨介质航行的无人机项目主要有如下：美国海军的“鸬鹚”水下发射跨介质无人机[1]，该项目计划将无人机通过潜射导弹发射筒发射，完成任务后采用减速伞减速并溅落入水，由无人潜航器回收；MIT的仿飞鱼跨介质无人机，该无人机已经实现短距离跨介质滑翔[2]；Siddall 等[3]设计了一款桨式推进仿鲣鸟两栖飞行器AquaMav，采用喷射方式从水下起飞，采用鲣鸟溅落式入水；Zufferey等[4]在AquaMAV的基础上设计了新一代跨介质航行器，不同之处在于新样机利用化学反应爆炸而不是高压气体来完成喷水动作，重点对出水过程进行了验证。Lu等[5]提出一种跨介质旋翼固定翼复合飞行器“哪吒”，具备垂直起降、平飞巡航、水下滑翔、水空多次穿越能力。William S等[6]-[7]开发了“鹰鳐”(EagleRay)固定翼跨介质航行器，可从水面起飞或潜入水下航行。目前所公开的跨介质无人机主要存在如下问题：单一的外形难以满足水空两相的航行特点；可实现的飞行距离一般较短；飞行速度较慢，一般为亚音速；一般为常规布局，空中隐身效果较差；以单次跨越介质模式为主，难以同时实现多次跨越介质；跨越介质时普遍噪声较大。本文中所设计的变形仿生飞翼跨介质无人机(deformable bionic flying-wing aerial-aquatic unmanned vehicle，DBFAUV)外形采用飞翼布局，结合头部仿生设计，相比于传统常规布局跨介质无人机更重视隐身能力，且头部的仿生化设计带来了更小的入水水花和噪声，无尾的布局又能显著减低无人机在水下航行时的阻力，相比常规布局的跨介质无人机，隐蔽性更好，生存能力更强。通过CFD计算了该无人机空中飞行和水下航行的流场，验证了该外形设计具有良好的气动和水动特性。

2 变形仿生飞翼跨介质无人机外形设计

传统的航空飞行器以及水下航行器在外形方面存在巨大的差异，这是由于航行介质的不同导致的。水的密度以及黏度都大大高于空气，根据相似原理，同样的外形在相同速度下在水中航行产生的升力是空中的14倍，因此，跨介质无人机在空中需保持较高速度飞行，在水中需保持较低的速度和较大的负攻角航行，然而，较大的负攻角所导致的诱导阻力又使得无人机较难在水中航行。借鉴传统的航空飞行器的外形设计，提出了一种兼顾水空两相航行的变形无人机外形，同时该外形兼顾隐身效果以及入水的稳定性和降噪。

该跨介质无人机的工作模式为“单次入水，上浮海面回收”，无人机由陆地或者军舰上的发射装置发射，随后无人机开始飞行，飞行高度为10～20 km，飞行速度为马赫数0.78；到达预定位置后，无人机开始准备入水。无人机入水前减速到30 m/s，且将机翼外部向下折叠至机身腹部；入水过程采用滑翔溅落入水；入水之后机身翻转180°，折叠后的机翼产生的负升力用以抵消浮力，随后无人机开始水下作业，以最大10 m/s的速度航行，任务完成后上浮至海面完成回收。

该跨介质无人机头部模仿鲣鸟头部设计，以此期望降低在入水时空泡对无人机的影响，鲣鸟从其鸟喙尖端到头部的直径逐渐增大，鲣鸟在入水时能够使水流流向身后，溅起少量的入水水花，从而使入水姿态更容易被控制以及降低入水噪声。该跨介质无人机采用飞翼布局，机翼采用中等后掠角可折叠变形翼，兼顾空中隐身效果以及水下航行减阻，无人机在空中飞行时，机翼完全展开以增加升力，在水下航行时，机翼外部向下折叠至飞机腹部，减少无人机在水下的阻力，同时，无尾的设计能够进一步减少该无人机在水下航行时受到的阻力。

空中飞行状态下的DBFAUV外形如图1所示，水下航行状态的DBFAUV外形如图2所示。溅落入水时的DBFAUV外形如图3所示。

图1 DBFAUV在空中飞行状态下的外形图Fig.1 Conceptual diagram of the DBFUAV in the air

图2 DBFAUV在水下航行状态下的外形图Fig.2 Conceptual diagram of the DBFUAV in the water

图3 DBFAUV在溅落入水时的外形图Fig.3 Conceptual diagram of the DBFUAV splashing into the water

3 数值方法及网格

3.1 计算模型和网格

本文中所述无人机在流体中航行时，涉及到复杂的湍流问题，采用工程应用中较为常用的雷诺平均法，通过引入湍流模型封闭方程组，求解湍流要素的时均值。

本文中网格划分采用非结构化网格，计算域设置为长为16 m，半径为6 m的圆柱体，无人机顶端距计算域入口6 m。并且对无人机头部、尾部、机翼等曲率变化较大的位置进行加密处理，且对机翼后缘、水下机翼折叠处等流场参数变化剧烈的区域进行加密处理。图4为该跨介质无人机空中状态下的网格划分及壁面Y+分布云图，图5为水下状态的网格划分及壁面Y+分布云图，空中状态下的网格数量约为700万，水下状态的网格数量约为800万。空中状态的壁面法向网格第一层的高度定为0.000 001 6，边界层总高度为0.001，水下状态的壁面法向网格第一层的高度定为0.000 002 8，边界层总高度为0.001，经检验，本文中所述2种状态下的网格的近壁面处的Y+值均在1以下。

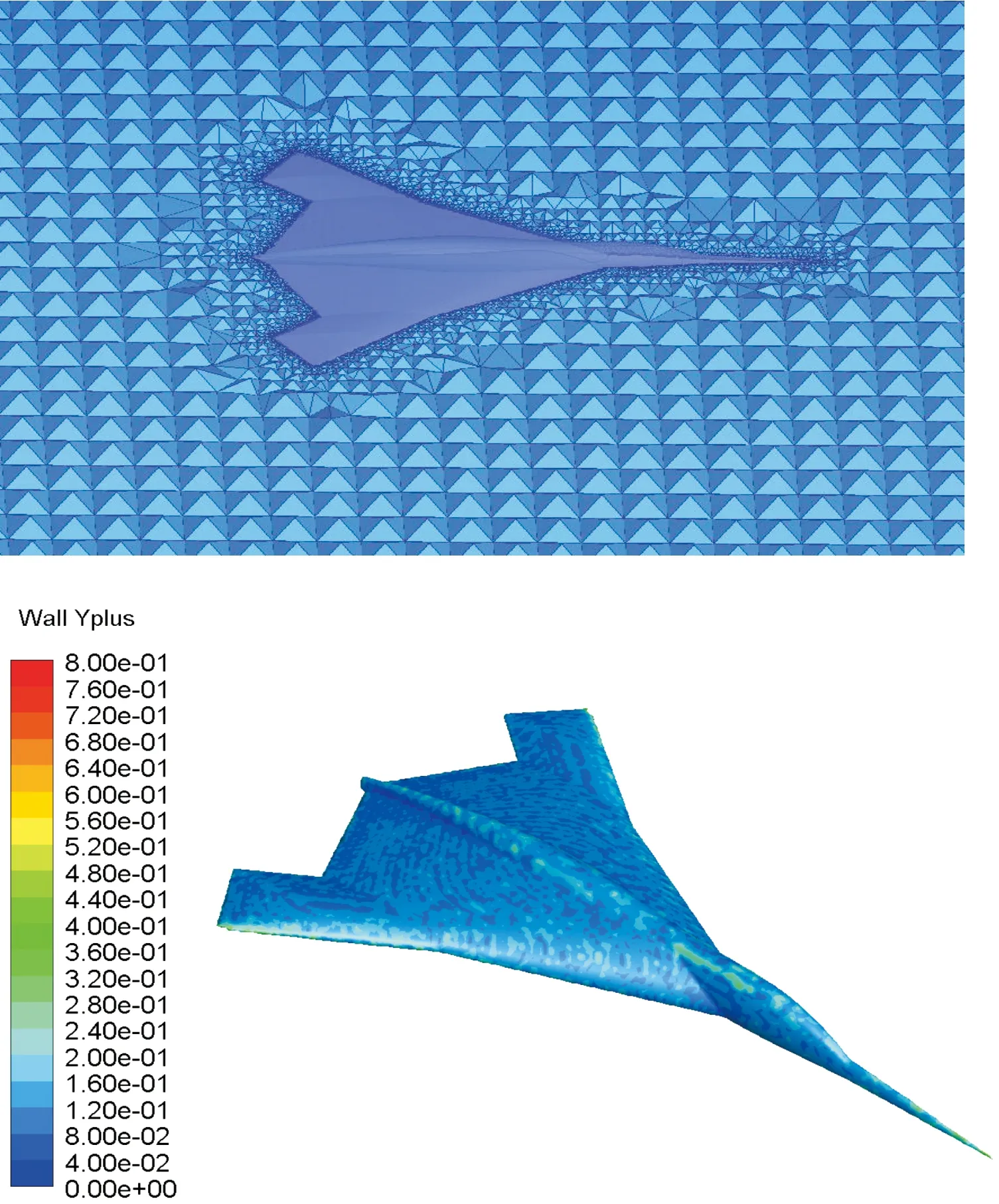
图4 DBFAUV在空气介质中的网格及Y+分布云图Fig.4 Mesh generation of the DBFAUV in the air phase and the contour of wall Y+

图5 DBFAUV在海水介质中的网格及Y+分布云图Fig.5 Mesh generation of the DBFAUV in the water phase and the contour of wall Y+

3.2 控制方程

本文中所涉及到的控制方程主要包括质量守恒方程、动量守恒方程和能量守恒方程。文献[1]给出其通用形式如下，

(1)

3.3 湍流模型

选取基于SST(Shear stress transport)的k-ω方程模型，其考虑了湍流剪切应力的传播，能够很好的处理近壁面处低雷诺数的数值计算，并且同样具备k-ω模型对于远场计算的优点，其对于不同界面的处理具有较好的适应性，收敛效果好。

k-ω模型求解了2个运输方程，分别为湍动能方程和湍流频率方程：

(2)

(3)

式中：Pk为层流产生的湍流动能；σk和σω分别为湍动能方程和湍流频率方程的湍流能量普朗特数，湍流黏度μt与湍动能和湍流频率有关，其关系式为：

(4)

3.4 边界条件

无人机壁面采用无滑移壁面，采用亚松弛因子默认值计算初场。流体入口的边界类型为压力远场条件。选择笛卡尔坐标系速度分量定义方式，速度分量随无人机攻角变化而变化。

首先对无人机空中气动特性进行研究，选择基于密度的隐式求解器，计算域内介质为空气，表压设定为101.33 kPa，合速度大小分别设置为马赫数0.5，0.65和0.78。

对无人机水下水动特性进行研究时，选择基于压力的隐式求解器，计算域内介质设置为海水，表压设置为160 kPa，合速度大小分别设置为1 m/s，5 m/s，10 m/s。

图6为无人机在空中以马赫数0.78的速度0°攻角飞行时的表面压力云图。由图中可以看出，无人机头部、翼前缘形成高压区，机身中部及翼中部产生低压区，与实际工程经验相符。图7为流场剖面速度云图，由图中可看出，飞机背部中段局部速度较高，从而产生较大升力。

图6 DBFAUV在空中飞行时的表面压力云图 (马赫数0.78，攻角为0°)Fig.6 Surface pressure contour of the DBFAUV at the speed of Mach Number 0.78 with 0° attack angles

图7 DBFAUV在空中飞行时的流场剖面速度云图 (马赫数0.78，攻角为0°)Fig.7 Velocity contour of the flow field at the speed of Mach Number 0.78 with 0° attack angle

4 计算结果分析

本文中计算了无人机空中飞行时速度在马赫数0.5，0.65，0.78下，攻角在-15°变化到15°共27个状态之下的流场。计算了无人机在水下航行时在1 m/s，5 m/s，10 m/s的航行速度下，攻角在-30°变化到30°共39个状态之下的流场。

图8为该DBFAUV在空气中的阻力系数随攻角变化曲线，由图可以看出：阻力系数的最低点对应一小的负攻角，阻力基本上以最小点处成对称分布，且阻力在-5°到5°攻角范围之内变化平缓，当攻角小于-5°或超过5°时，DBFAUV的阻力急剧上升，这是由于其迎风面积的增加造成的。

图8 DBFAUV空气中的阻力系数随攻角变化曲线Fig.8 Drag coefficient curve of the DBFAUV in the air with attack angle

图9为该DBFAUV在空气中的升力系数随攻角变化曲线，由图可以看出：升力系数随攻角的增加而增加，且在攻角超过12°之后变化平缓。升力系数的零点对应一小的负攻角，约为-4°。0°攻角时飞机产生正升力，且在攻角较小时，即可产生较大升力。

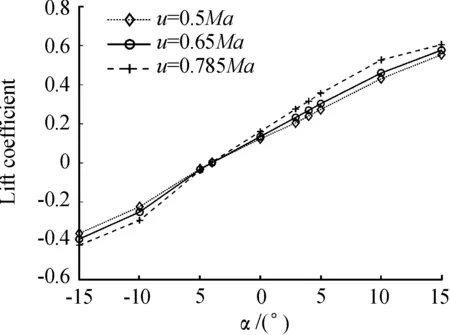
图9 DBFAUV空气中的升力系数随攻角变化曲线Fig.9 Lift coefficient curve of the DBFAUV in air with attack angles

图10为该DBFAUV在空气中的升阻比随攻角变化曲线，由图可以看出：当攻角到达4°左右时，升阻比达到最大，因此，根据航程计算公式，保持攻角在4°左右小范围内变化是减小阻力增大航程的关键。

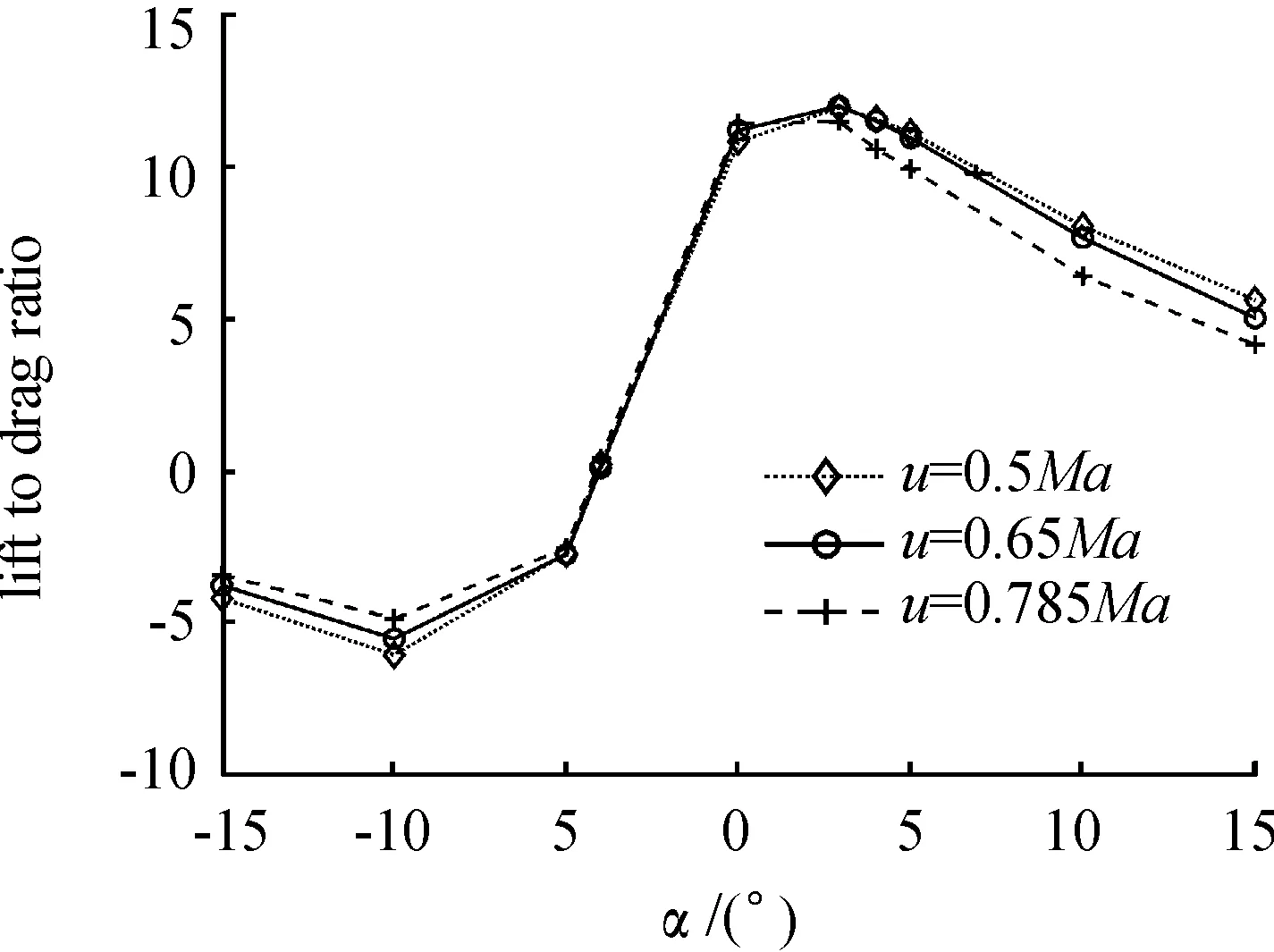
图10 DBFAUV空气中的升阻比随攻角变化曲线Fig.10 Lift to drag ratio curve of the DBFAUV in air with attack angles

图11为无人机在水中以5 m/s的速度0°攻角航行时的表面压力云图。由图中可以看出，无人机的头部、翼前缘、翼后缘以及翼折叠处形成高压区，无人机的上翼面前部，下翼面中部产生低压区，与实际的工程经验较为相符。图12为流场剖面速度云图，由图中可看出，在实际航行过程中，由于无人机在水下翻转180°航行，在翼折叠后无人机下表面中段的流体流速较高，从而产生向下的升力。

图11 DBFAUV在水中以5 m/s的速度0°攻角 航行时的表面压力云图Fig.11 Surface pressure contour of the DBFAUV sailing in water at a speed of 5 m/s with 0° attack angle

图12 DBFAUV在水中以5 m/s的速度0°攻角 航行时的流场剖面速度云图Fig.12 Velocity contour of the flow field at a speed of 5 m/s with 0° attack angle

图13为该DBFAUV在水中翻转与不翻转航行时的阻力系数随攻角变化曲线，由图可以看出：该无人机在翻转180°航行时，当攻角为2°左右时，DBFAUV所受阻力最小，且当攻角在2°到4°之间时，阻力系数几乎无变化。当无人机处于负攻角时的阻力系数曲线变化相比正攻角时更为平缓。且阻力在0°到5°攻角范围之内变化较小，当攻角小于0°或超过5°时，DBFAUV的阻力系数开始快速上升，这是由于其迎风面积的增加造成的。因此，保持攻角在2°到4°之间变化是减小水下阻力的关键。

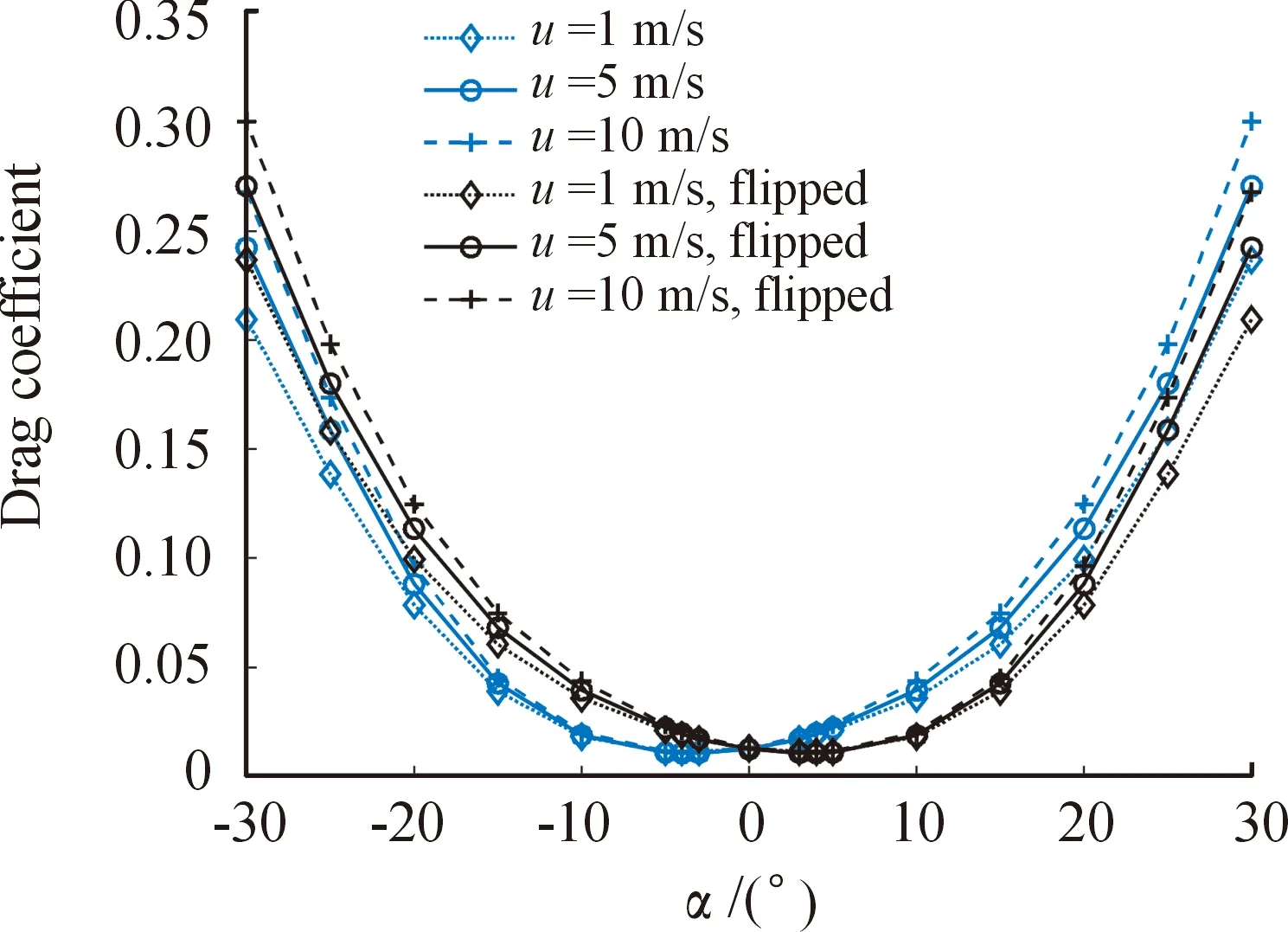
图13 DBFAUV在水中翻转与不翻转的阻力系数 随攻角变化曲线Fig.13 Drag coefficient curve of the DBFAUV in water with attack angles

图14为该DBFAUV在水中翻转与不翻转航行时的升力系数随攻角变化曲线，由图可以看出：该无人机在翻转180°航行时，该无人机的升力系数随攻角的增加而减小，大体上成线性变化。零升力攻角约为5°。0°攻角时飞机产生负升力，且在攻角在5°左右进行小范围变化时，产生的升力较小，同时阻力也较小，故可以通过控制攻角在5°左右来实现飞机在水下的配平与减阻。

图14 DBFAUV在水中翻转与不翻转的升力系数 随攻角变化曲线Fig.14 Lift coefficient curve of the DBFAUV in water with attack angles

此外，不难看出，若该无人机在水下翻转180°航行，升力与浮力配平后其受到的阻力将更小。这是由于该无人机的密度小于水的密度，以所述DBFAUV为例，其在水下存在正浮力ΔB=200 N，若要配平升力和正浮力，则该无人机需要产生的负升力大小为-ΔB=-200 N，则当无人机翻转180°时，则可推得其在航行速度为10 m/s时的升力系数为-0.002，由图14可得其配平攻角为4.8°，其对应的阻力系数为0.020 5，同理可得当无人机不翻转时，配平攻角为5.3°，则其对应的阻力系数为0.021 3，翻转相比不翻转阻力系数减小了3.8%，从而可看出当该无人机在水下翻转航行能降低其阻力。

5 DBFAUV的航行动力学仿真

上文中描述了DBFAUV的外形设计和其基本的气动和水动特性。然而，为了研究该跨介质无人机外形在实际飞行状态下的机动性和操控性，对该飞行器进行动力学仿真是十分必要的。

设计用于该DBFAUV的组合式操纵系统，包括3对舵，分别为升降舵、副翼1以及副翼2。DBFAUV在空中飞行时，采用Bank to turn(BTT)倾斜转弯技术，通过3种舵机的联动倾斜机身，靠升力来改变方向，且靠升降舵来控制高度，其控制系统的舵面组成如图15所示。DBFAUV在水下航行时，副翼1与副翼2组合成一个开合式襟翼，通过该开合式翼控制飞行器的方向，采用Side to turn(STT)侧滑控制技术直接通过“摆动”来控制方向，且与空中飞行类似，DBFAUV在水下靠升降舵来控制深度，水下控制系统的舵面组成如图16所示。

图15 DBFAUV在空中飞行时的舵面组成示意图Fig.15 Composition of control surface of DBFAUV in the air

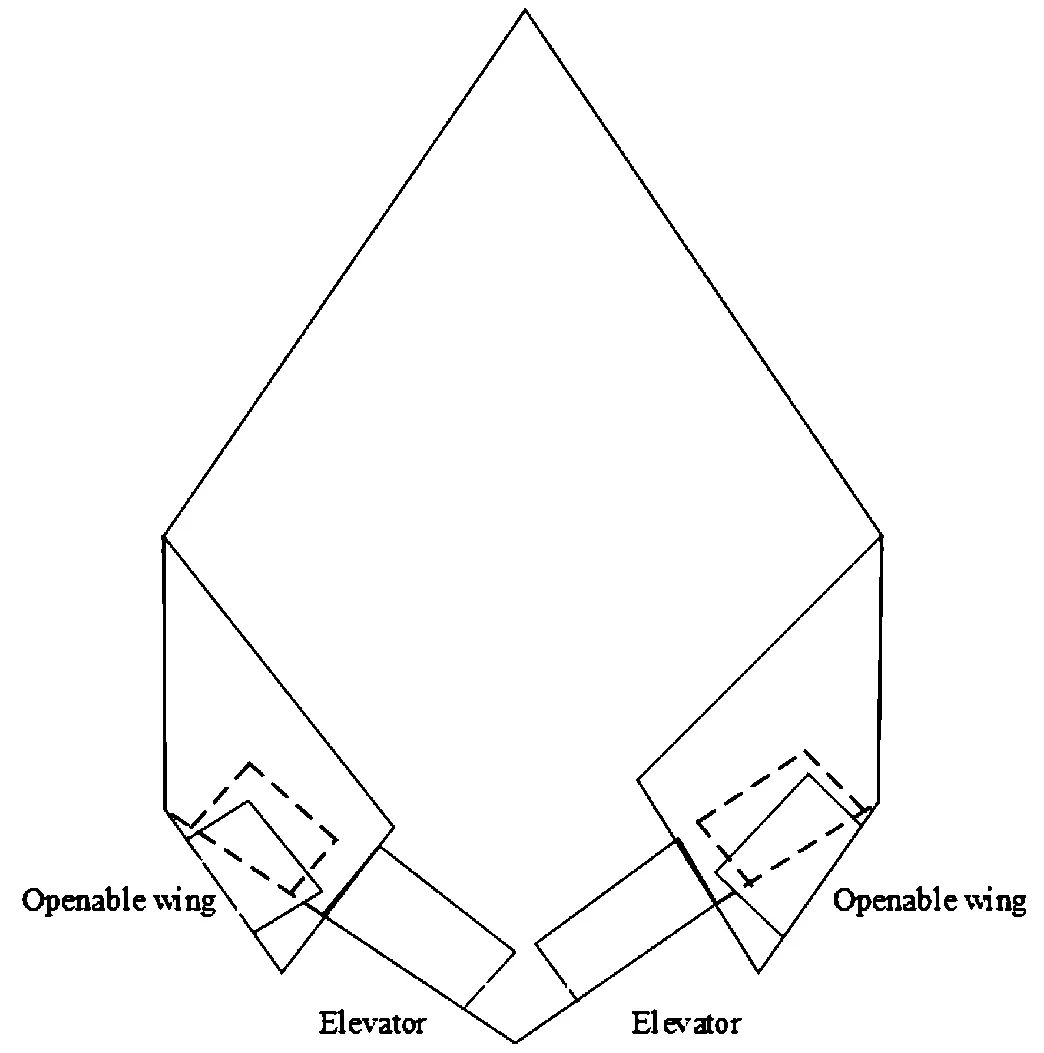
图16 DBFAUV在水中航行时的舵面组成示意图Fig.16 Composition of control surface of DBFAUV in the water

通过CFD以及工程估算法得到该DBFAUV在飞行状态下的气动数据以及水下航行时的水动数据[10]。在Simulink中采用S-函数建立其2种状态下的动力学模型[11]，如图17所示。采用PID控制技术设计空中飞行以及水下航行的控制系统[12]，用以测试该飞行器在2种状态下的机动和操控性能，无人机在空气中和水下的舵效由CFD方法获得。无人机的总体数据和仿真过程中的基本信息如表1所示。无人机在空气中的舵效信息如表2所示，无人机在水中的舵效信息如表3所示。

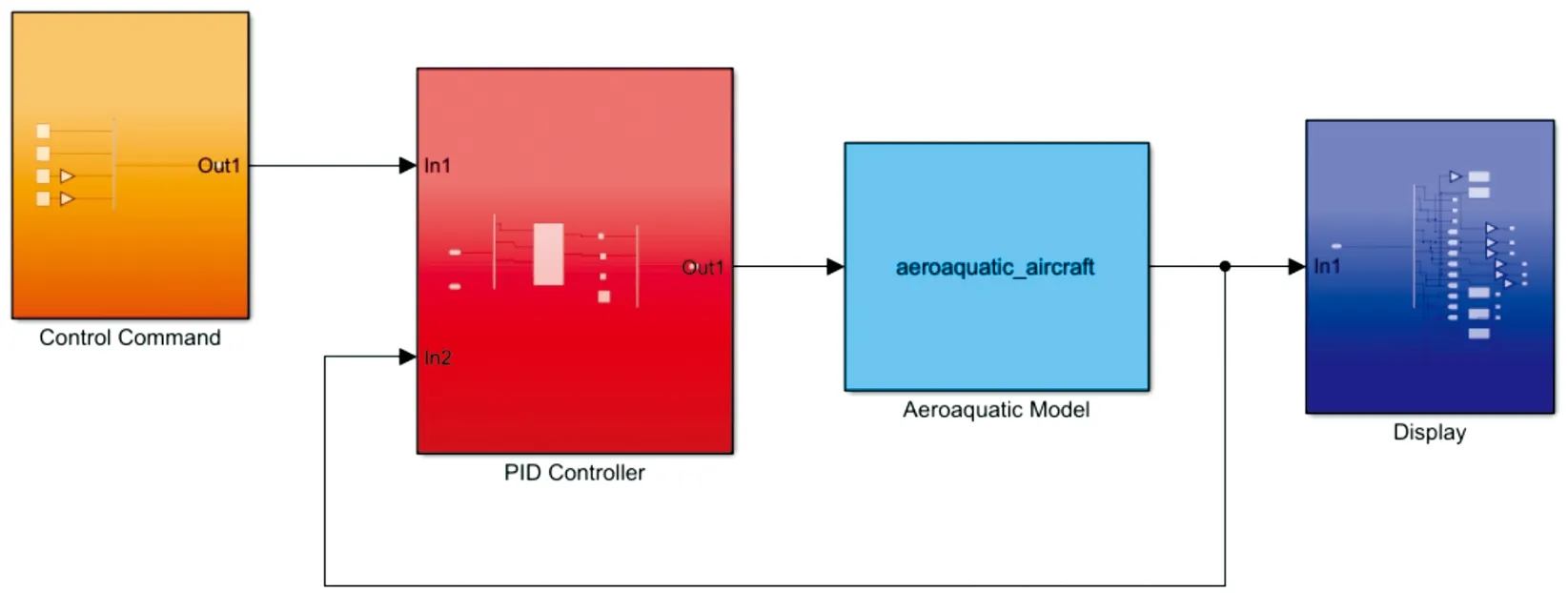
图17 采用S-函数的DBFAUV的动力学仿真模型示意图 Fig.17 Dynamic simulation model of the DBFAUV using S-Function

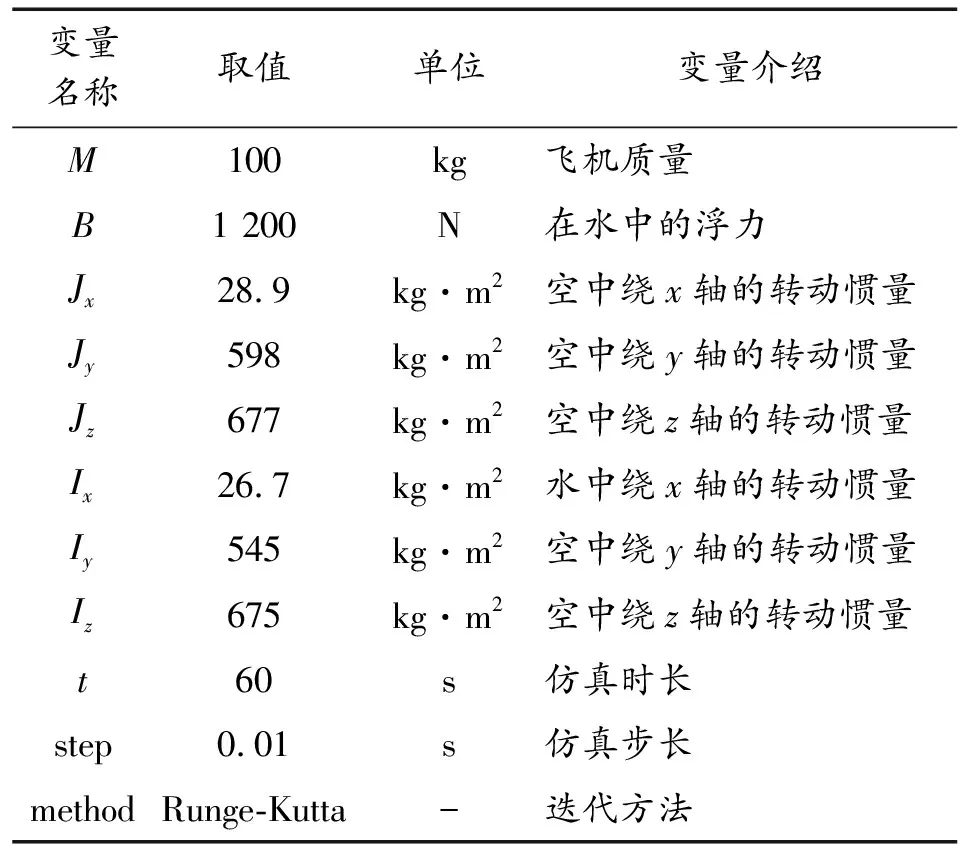
表1 无人机的总体数据及仿真基本信息设置Table 1 General data and basic simulation information setting of the DBFAUV

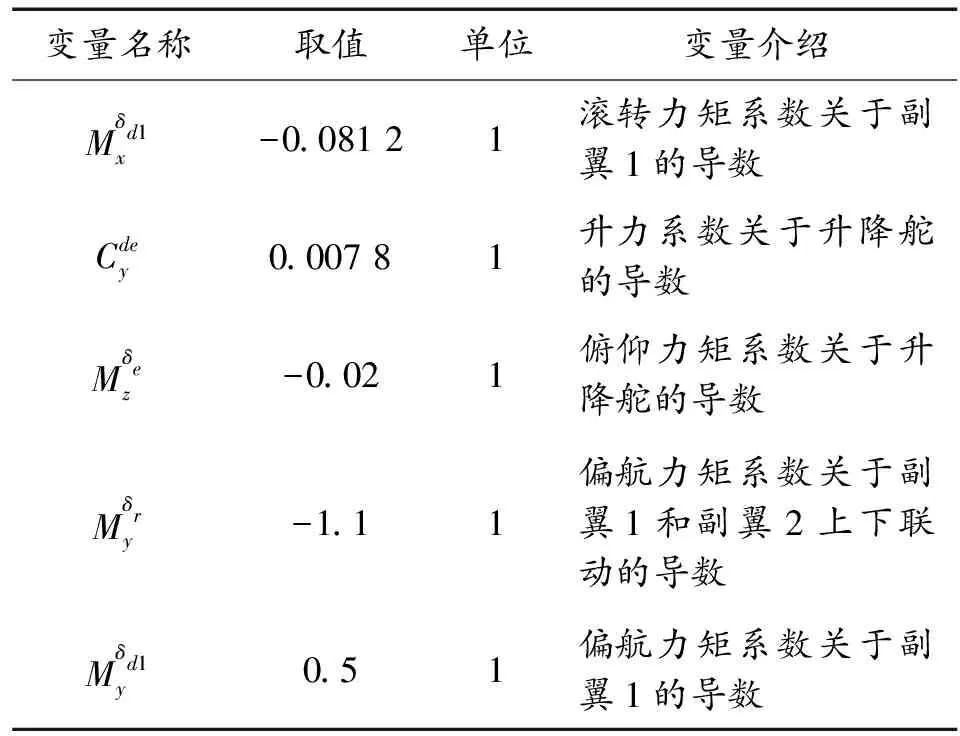
表2 无人机在空气中的舵效信息

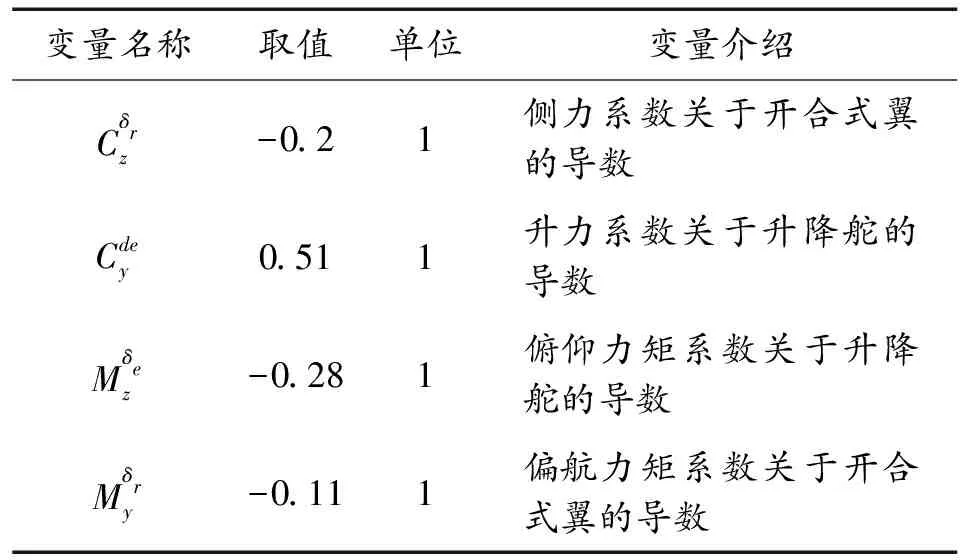
表3 无人机在水中的舵效信息

图18为该DBFAUV在空中以200 m/s的速度下，高度从距离海平面200 m下降到170 m，且同时偏航角由正北0°变为北偏西30°时的高度变化曲线°，图19为该过程的偏航角变化曲线。由图可看出，本文中所设计的飞行器在空中可以通过升降舵的改变来实现纵向高度的变化，以及通过升降舵与副翼的配合以倾斜转弯的方式实现航向的变化，且高度调整以及偏航角变化较为精准迅速，超调量小，故该无人机在空中操纵性较好。

图18 DBFAUV在空中的高度变化曲线Fig.18 Height curve of the DBFAUV in the air

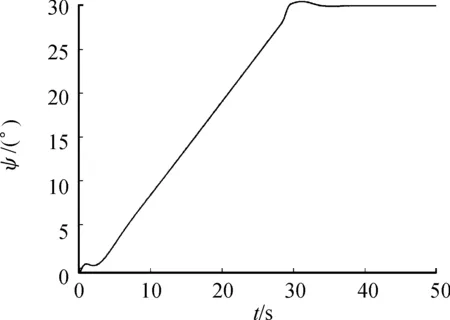
图19 DBFAUV在空中的偏航角变化曲线Fig.19 Pitch angle curve of the DBFAUV in the air

图20为该DBFAUV在水下以10 m/s的速度下，深度从距离海平面200 m上升到170 m，且同时偏航角由正北0°变为北偏西30°时的深度变化曲线，图21为该过程的偏航角变化曲线。由图可看出，本文中所设计的飞行器在水中可以通过升降舵的改变来实现纵向深度的变化，以及通过开合翼以侧滑转弯的方式实现航向的变化，深度以及偏航角的改变过程均在15 s内完成，且无超调，证明该无人机在水下操纵较为灵活且平稳。

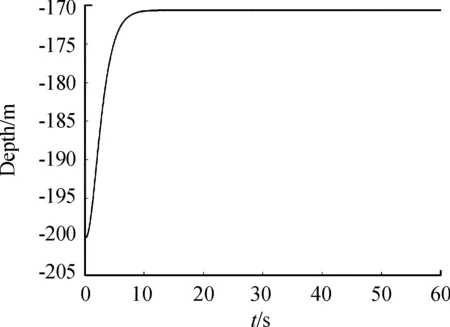
图20 DBFAUV在水中的深度变化曲线Fig.20 Depth curve of the DBFAUV in the water

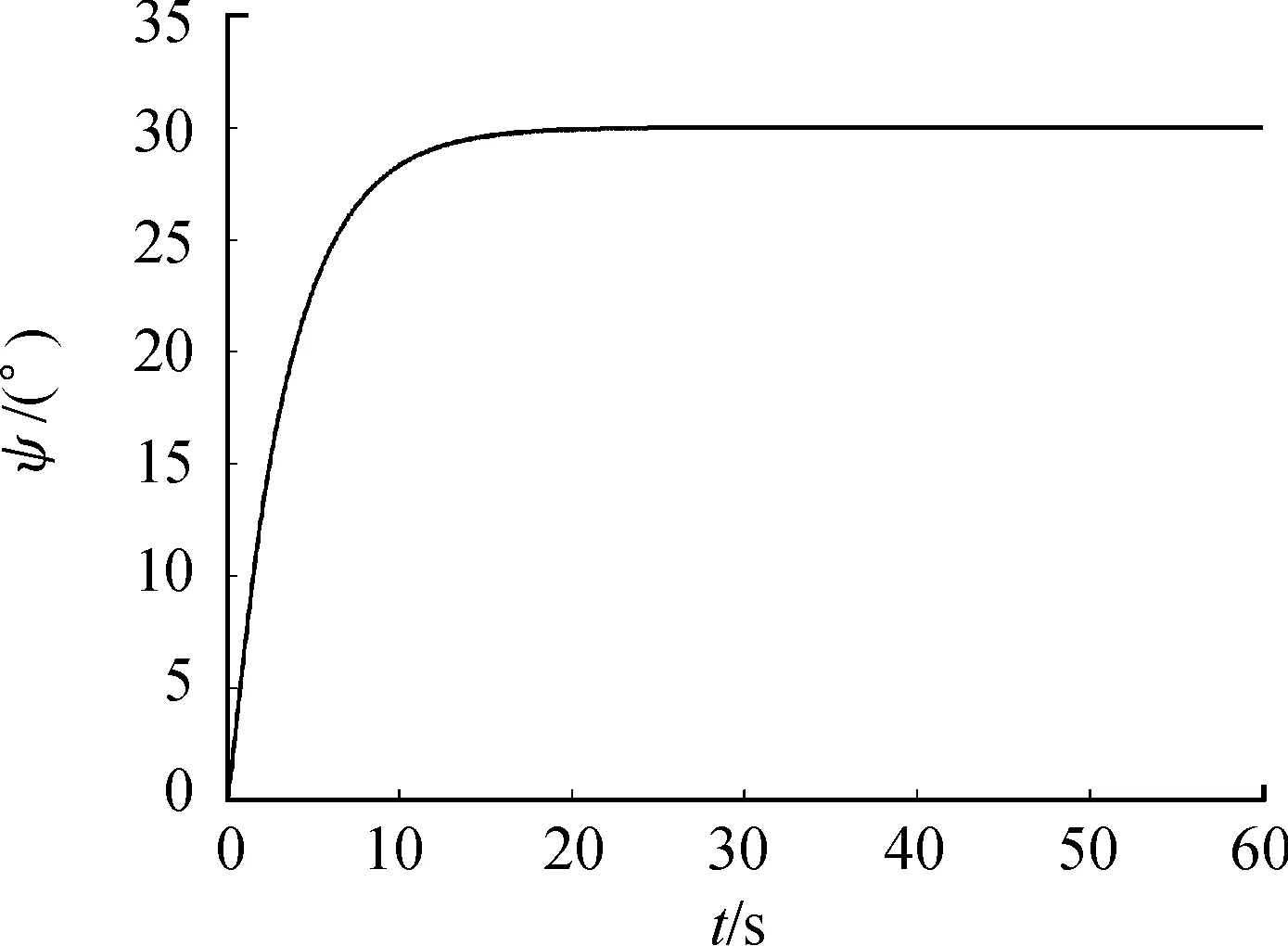
图21 DBFAUV在水中的偏航角变化曲线Fig.21 Pitch angle curve of the DBFAUV in the water

6 结论

1) 所设计的无人机在空中飞行时具有良好的升阻特性，攻角较小时阻力较小，升阻比较大。且该无人机能够通过变形获得较好的水下航行能力，其水下阻力在小攻角时较小，且其变形后的机翼提供的升力能够抵消无人机的正浮力，能够达到气动性能和水动性能的良好平衡。

2) 所设计的无人机密度比水小，需要利用飞机产生的升力抵消正浮力，使无人机在水下翻转180°航行，可利用升力抵消正浮力获得更小的航行阻力，增大航程。

3) 所设计的无人机在空中能够通过升降舵和两组副翼的联动实现控制高度以及航向，在水下能够通过升降舵和由副翼组成的开合式翼分别控制深度和航向，在2种介质中的机动性与操控性均达到平衡。

4) 作者将在以后重点研究该无人机在入水过程中进一步减少水花以及降低噪音等问题。