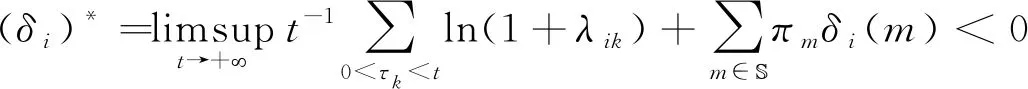一类具有Markov切换和脉冲效应的两种群竞争模型的生存性分析

贺小杰，王清龙，刘志军

(湖北民族大学 数学与统计学院，湖北 恩施 445000)

基于经典的Lotka-Volterra模型，Gopalsamy[1]提出了一类具有饱和效应的两种群竞争模型.随后许多学者对该模型和以该模型为基础延伸的新模型进行广泛的研究并取得了较好结果，主要涉及持久性、稳定性、分支问题和概周期解等方面[2-6].特别是2020年胡静和刘志军[6]研究了如下一类具有耦合噪声和饱和效应的两种群竞争模型：

(1)

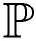
在现实环境中种群可能会受到一些较为剧烈的环境扰动，例如洪水、寒流、干旱等.这些扰动可能会导致种群的生存环境迅速由一个状态切换为另一个状态，从而改变种群的增长率[7-8].通常情况下，不同环境之间的切换是无记忆的，且在每个状态停留的时间是服从指数分布的.因此，可以用一个具有有限状态空间={1,2,…,N}的右连续Markov链α(t)来描述这一类生态系统中的随机因素[9-11].此外，种群的增长可能会在某些固定的时刻受到相对较短时间间隔的作用，如投放、捕获等，这会使得种群数量在短期内发生跳跃性的变化，在数学上通常把这种变化以“脉冲”形式进行体现[12-13].近年来一些学者研究了具有白噪声扰动和脉冲效应的种群模型[14-18]，然而研究具有Markov切换和脉冲效应的多种群模型较少.受上述思想的启发，本文拟在模型(1)的基础上考虑如下一类具有Markov切换和脉冲效应的两种群竞争模型:

(2)

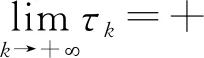
1 准备知识

令α(t)的生成元Λ=(γij)N×N由下式确定：

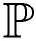
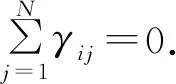
为方便后面的讨论，给出如下符号标记：

+=(0,+∞)，

在全文中假设下面(A1)和(A2)始终成立：

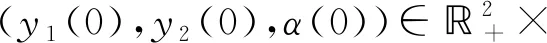
证明考虑如下一个具有Markov切换无脉冲的随机微分模型：

(3)

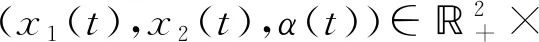
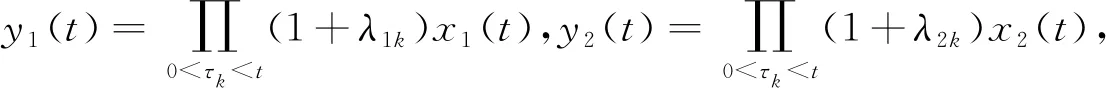
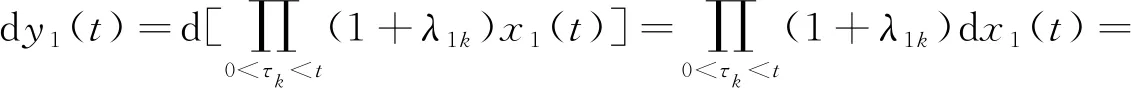
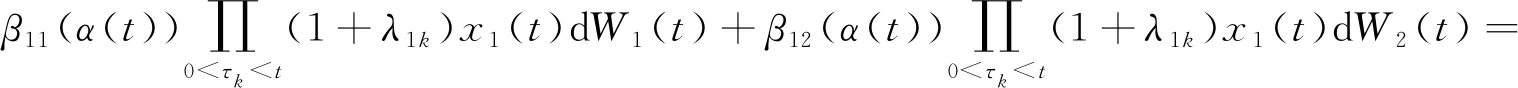
同理可得

β21(α(t))y2(t)dW1(t)+β22(α(t))y2(t)dW2(t).

在每个间断点τk∈+，k∈处，右极限满足

左极限满足

2 灭绝性与持久性

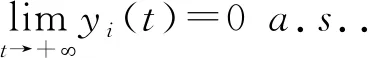
β11(α(t))dW1(t)+β12(α(t))dW2(t)，

对上式两端由0到t积分有

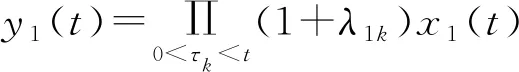
(4)

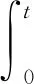
根据鞅的强大数定律[9]可以得到

(5)

对式(4)两边同时除以t有

根据α(t)的遍历性和式(5)可以得到

当(δ2)*<0时，类似上面的讨论可以证明种群y2灭绝.证毕.

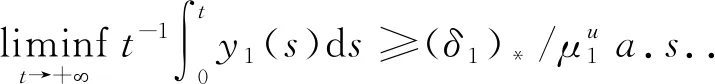
因此对所有t>T，将上述不等式代入式(4)可以得到

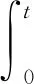
(6)

因此,

对上式使用洛必达法则得到

由于ε>0是任意小的，因此当(δ1)*>0时可以得到种群y1是强平均持久生存.

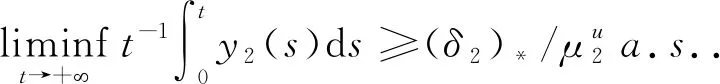
证明定理3与定理2的证明类似，故省略.

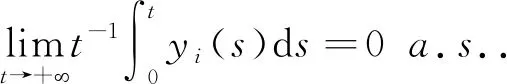
证明对于任意小的ε>0，存在T>0,使得当t>T时有

将上述不等式代入式(4)获得

其中η1=(δ1)*+ε/2.经过类似式(6)的计算可以得到

因此有

进一步通过使用洛必达法则可得

由于ε是任意小的.因此当(δ1)*=0时可以断定种群y1会非平均持久生存.

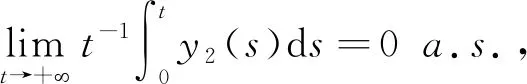
3 数值模拟和讨论

通过数值模拟来支持理论分析结果.对于模型(2)取τk=k，k∈，λik=e(-1)k+1/k-1，那么此时脉冲条件λik满足假设(A2)，即脉冲有界.当脉冲有界时通过定理1～4可知由此可以发现有界脉冲对种群灭绝和持久没有影响.

(i) 对于种群y1，当2种状态下其他参数不改变时，取π11=0.55，通过计算可以得到(δ1)*=-0.01<0，根据定理1可知此时种群y1灭绝(见图1(a)).对于种群y2，当2种状态下其他参数不改变时，取π21=0.4，通过计算可以得到(δ2)*=-0.002 5<0，根据定理1可知此时种群y2灭绝(见图1(b)).

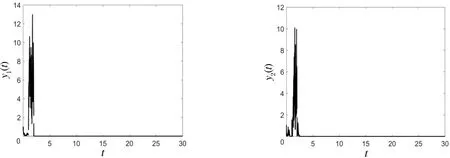
(a) 当π11=0.55时种群y1灭绝(b) 当π21=0.4时种群y2灭绝图1 两种群灭绝Fig.1 Extinction of the two species

(ii) 对于种群y1，当2种状态下其他参数不改变时，取π11=0.65，通过计算可以得到(δ1)*=0，根据定理4可知此时种群y1非平均持久(见图2(a)).对于种群y2，当2种状态下其他参数不改变时，取π21=0.425，通过计算可以得到(δ2)*=0，根据定理4可知此时种群y2非平均持久(见图2(b)).

(iii) 对于种群y1，当2种状态下其他参数不改变时，取π11=0.8，通过计算可以得到(δ1)*=0.015>0，根据定理2可知此时种群y1强平均持久(见图3(a)).对于种群y2，当2种状态下其他参数不改变时，取π21=0.4，通过计算可以得到(δ2)*=-0.002 5<0，根据定理2可知此时种群y2灭绝(见图3(b)).

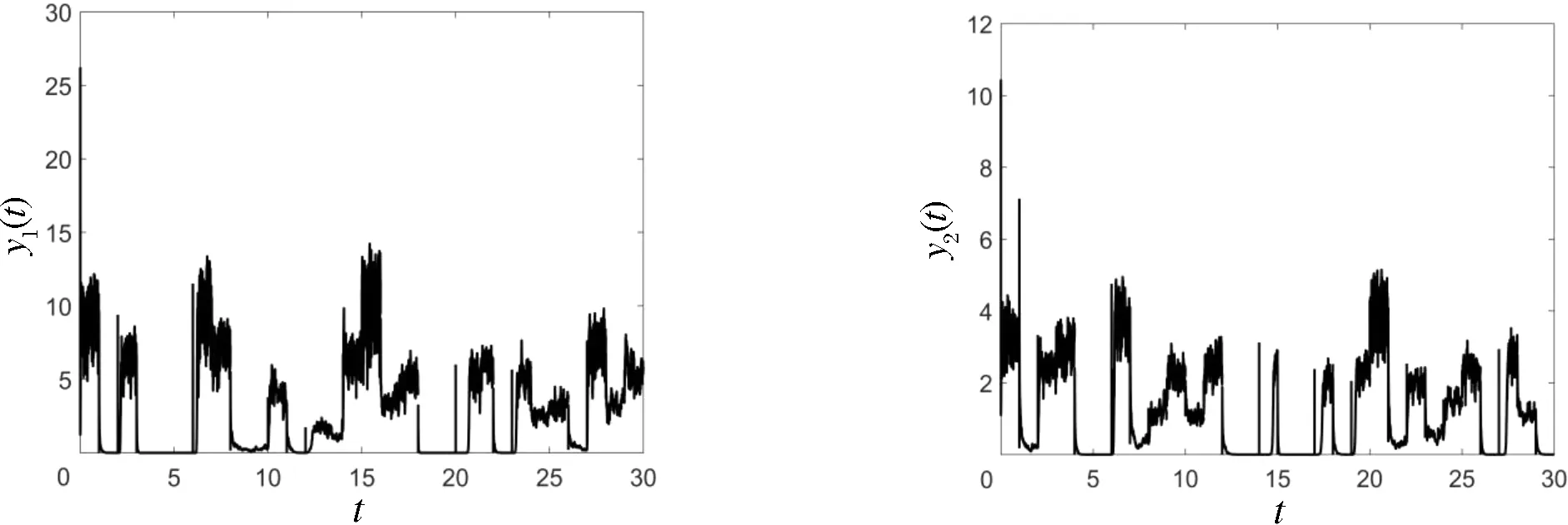
(a) 当π11=0.65时种群y1非平均持久 (b) 当π21=0.425时种群y2非平均持久图2 两种群非平均持久Fig.2 Non-mean persistence of the two species

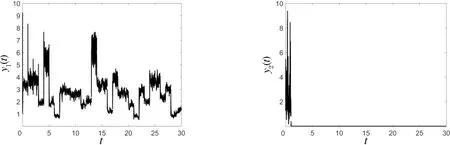
(a) 当π11=0.8时种群y1强平均持久(b) 当π21=0.4时种群y2灭绝图3 两种群部分持久Fig.3 Partial persistence of the two species

根据上述讨论结果(i)～(iii)可以发现，随着π的变化种群的灭绝和持久状态也会发生变化，即模型(2)中种群y1和y2的灭绝和持久与Markov链α(t)的分布π有着密切的关系.

4 结语