数字经济对农业全要素生产率的驱动影响

翟力红，王江鑫

（1.首都经济贸易大学，北京 100070；2.河北经贸大学，河北 石家庄 050000）

0 引言

在1994年出版的《数字经济》一书中，Don Tapscott详细阐述了这种新经济形态，用大量实证阐述了数字化应用给社会带来的重大影响［1］。此后国内外数字经济的内涵出现了不同的变化，其内涵囊括的信息逐渐全面。丁志帆等人将其理解为以数字化信息作为生产要素，将信息技术应用到传统产业以实现配置效率提升和结构优化的一种新经济活动［2］。然而量化数字经济对于经济社会的影响，通常是通过数字经济发展水平的测度、数字经济发展指数的测算以及选取合适的代理变量来进行。刘传辉从数字基础设施、数字产业基础、人力资源支撑等方面出发，将其定义为一级指标，并根据实际情况进行二级指标构建，之后采用熵权法构建了综合的数字经济发展水平综合测度体系，结果表明城市群之间的数字经济差异明显，呈现出了一定的波动性［3］。

全要素生产率本质上指总产出量占所有的生产要素投入量的比例情况，此外还可以将其分解为技术进步和综合效率影响，冯海发于1990年首次通过测度农业的全要素生产率来评价经济效率［4］。在此基础之上，有学者采用数据包络分析法（DEA）来进行测算。王霞云等人将产出指标定为第一产业（农、林、牧、渔业）总产值，并选取了以农作物播种总面积、农业机械总动力为代表的6个投入要素，采用DEA模型测算农业全要素生产率［5］。此外李展等通过一个全新的视角，即从KLEMSTFP出发测度中国农业在1980-2016年的变化情况［6］。张帆等通过分析其空间网络联动性发现，地理邻接关系对其有促进作用，但农业结构调整却对全要素生产率有反向影响［7］。

当前有诸多学者对于数字经济发展水平进行了较为科学的指标体系构建与测算，并且利用合适的方法计算了农业的全要素生产率，对其影响因素进行了进一步深化分析，但很少研究量化数字经济水平对农业全要素生产率的影响，当前更多的是二者之间关系的理论化研究，缺少实证分析。本文立足于中国农业数字经济发展水平现状，根据农业实时特点构建指标体系，并采用DEA-Malmquist指数模型综合测算农业全要素生产率，主要基于内地31个省份2014-2019的年面板数据，构建模型对数字经济发展水平和农业全要素生产率之间的关系做出量化分析，以期在数字化大背景下为农业的高质量发展提供政策建议。

1 指标体系的构建和测度分析

1.1 数字经济发展水平

1.1.1 指标体系的构建原则及指标解释

借鉴中国社会科学院农村发展研究所和北京农业信息技术研究中心发布的《乡村数字经济指标体系构建》以及《中国数字乡村发展报告（2020年）》等相关文献，结合农业发展的范围需求、大环境要求以及实时特点，从投入与产出的视角选取了数字基础设施水平、数字产业发展基础、农业数字化效益三个维度构建指标体系，如表1所示。

表1 数字经济发展水平指标体系

1.1.2 熵权法

本文通过对主客观赋权法的优缺点对比及其具体方法的对比分析，结合数据之间的内在统计规律，采用熵权法，几乎不受主观因素影响地得出较为客观的指标权重。由于本文涉及的指标体系均是正向指标，因此无需做非负化处理，结合实际的农业农村数字化特点，采用熵权法计算数字经济发展水平。

1.1.3 测度结果分析

采用熵权法确定权重后，各指标测算结果以及各个省份年度数据测算结果与年度排名如表2所示。

表2 31个省份2015-2019年的数字经济发展水平的测度结果（续表）

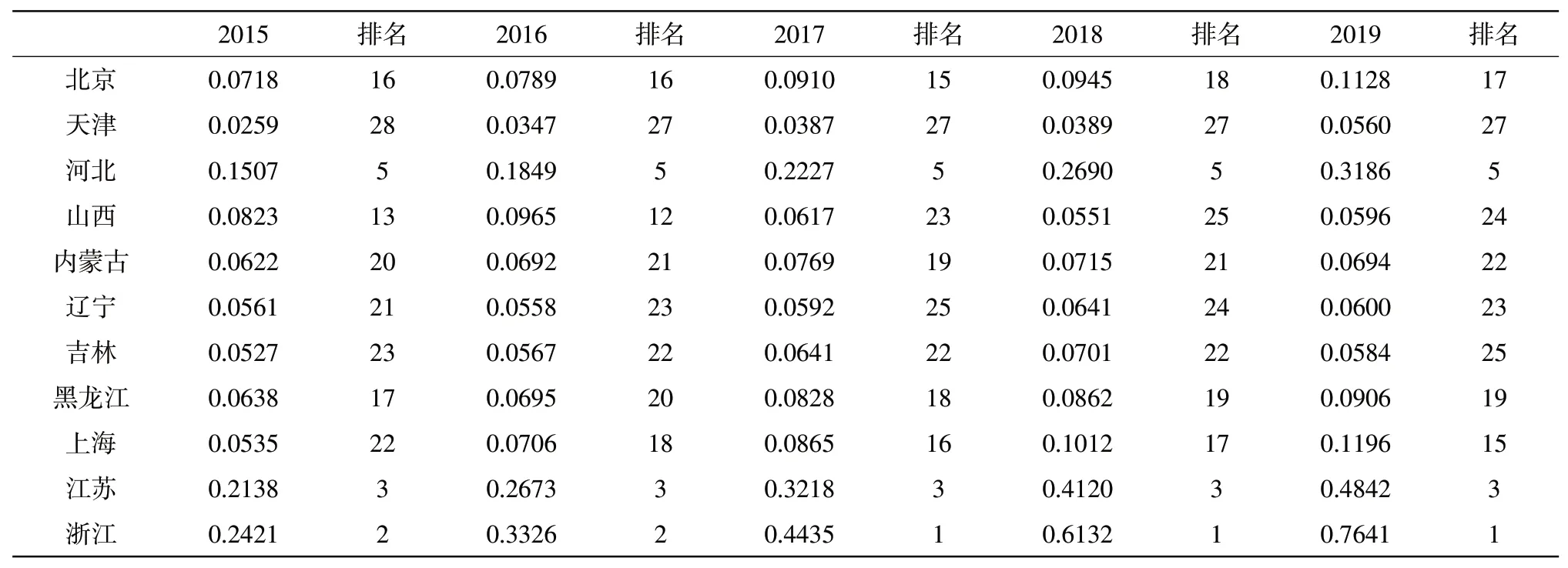
表2 31个省份2015-2019年的数字经济发展水平的测度结果

由表2可知，各个省份的数字经济发展水平均呈现出了上升的趋势，其中北京、上海、浙江等地的发展趋势明显，表明其数字经济发展水平较高，河北、内蒙古等地的数字经济保持相对平缓的速度，且在全国的排名也出现了小幅度的波动，海南、宁夏、青海等地区的数字经济发展水平逐年递增，但进步不太明显；此外，从横向看，河北、浙江、福建、广东、四川等地的数字经济发展水平相对较高，并且在全国处于较为领先的位置，表明这些地区农业相关的数字化投入以及数字化效益等方面效果显著，因此充分发挥数字经济发展水平的优势对于地区经济发展具有重要的意义。

1.2 农业全要素生产率

1.2.1 方法及理论的介绍

Malmquist指数是一种基于生产前沿发展起来的测量农业全要素生产率的有效方法，现今已经应用到各个行业的生产率测算中，由于它主要是通过计算数据包络分析（DEA）来实现，因此也常被称为DEA-Malmquist指数法。该方法不需要任何假设，只要提供必要的对象和指标便可进行求解。

借鉴文献［8］对于Malmquist指数的定义，其具体表达见公式（1），表3对其中变量进行了说明。

表3 DEA-Malmquist指数测算变量说明

1.2.2 指标体系的构建

根据上述测算方法的介绍，采用DEA-Malmquist指数法从投入与产出的视角来测算内地31个省份2015-2019年的农业全要素生产率。本文基于已有的研究成果和数据的可获得性，将产出变量定为农林牧渔业的总产值，将投入要素定为农林牧渔业以及相关行业服务的从业人员、农作物的播种面积、农业机械总动力、有效化肥施用量以及农业耕地灌溉面积，该部分投入一定程度上囊括了劳动、资本等生产要素的投入，并使得投入更加全面和具体，如表4所示。由于DEA分析的投入产出有无量纲的特点，所以不需要对单位进行调整，具体的投入产出变量选取如表4所示。

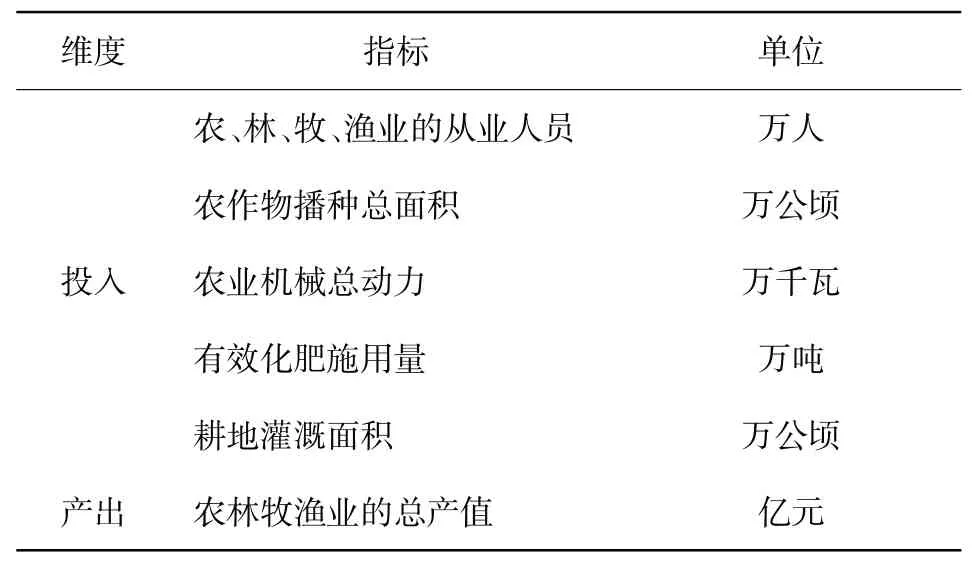
表4 农业全要素指标体系构建

1.2.3 测算结果分析

运用DEAP2.1软件对31个省份2014-2019年间的数据进行TFP的整体测算，并采用投入型与规模报酬不变作为基础条件，测算出农业全要素增长率，再将2014年作为基期类推进行连乘［9］，得到2015-2019年的TFP，具体结果如表5所示。

表5 31个省份2015-2019年的TFP数据

根据表5结果可知，从时间维度上来看，农业全要素生产率均呈现出了一定幅度的上升趋势，且最近几年都突破了1，实现了各投入要素资源配置效率、利用效率等的提升，技术进步明显，相对于2015年的数据，2019年的整体增速也愈发明显；从省份看，全国31个省份尽管都呈现出了进步的趋势，但各省份农业全要素生产率增速不一。基于2019年的数据做了一个三梯队划分，其中黑龙江、江西、湖南、重庆等8个省份的农业全要素生产率处在第一梯队，具有很高的水平，北京、天津、山西等15个省份在第二梯队，河北、内蒙古、上海等8个省份在第三梯队。

1.3 数据来源

综合指标体系的构建数据来源于《中国统计年鉴》《中国农村统计年鉴》、阿里研究院、国家统计局以及各省市的统计年鉴等，选取31个省份2014-2019年的数据（测算结果为2015-2019年）。个别缺失的数据用其临近年份的数值来代替。

2 数字经济对农业全要素生产率的影响分析

2.1 变量选取与数据说明

为分析数字经济发展水平对农业全要素生产率的影响，本文选择了回归模型作为分析方法，模型中的分析变量如下。

被解释变量：农业的全要素生产率。该变量数据是基于31个省份2014-2019年的投入产出要素，采用DEA-Malmquist指数法进行测度的结果，同时，为进行稳健性测试，本文选用索洛余值法测算的农业全要素生产率作为被解释变量的替换变量，用tfp3来表示。

核心解释变量：数字经济发展水平。该变量的测算是基于数字基础设施水平、数字产业发展基础、农业数字化效益等方面进行的综合评价。

控制变量：根据农业发展特点选取除数字经济发展水平外的一部分能够对被解释变量产生影响的变量。

（1）农村经济发展水平。本文主要用人均GDP来衡量该变量。

（2）自然灾害。本文用31个省份的受灾面积占农作物播种总面积表示某一地区农业环境的恶化程度。

（3）工业化程度。本文通过非农GDP与地区GDP的比重来表示地区的工业化发展水平。

（4）财政支农力度。财政支农力度主要是通过财政中农业农民支出占一般预算支出的比例来衡量。

（5）农业结构调整。本文主要通过粮食作物播种面积与农作物播种面积的比例来衡量农业的结构调整。

2.2 模型构建

构建回归模型如式（2）：

其中，被解释变量：i表示省份，t表示年份，TFPit表示农业全要素生产率；核心解释变量：digitalit表示数字经济发展水平；Xit表示一系列控制变量，包括经济发展水平ecoit、自然灾害ndisait、工业化程度indusdegit、财政支农力度supagriit、农业结构调整strucait；μi表示个体固定效应，可以解决不随时间变化而随省份而异的不可观测因素带来的问题；νt表示时间固定效应，能够解决不随省份变化而随年度变化的不可观测因素带来的问题；εit表示随机扰动项。

2.3 实证结果分析

针对上述模型，使用stata12分别拟合了混合回归、个体固定效应、同时控制了个体和时间效应的双向固定效应、随机效应模型，拟合的具体结果依次在表6的（1）-（4）列。

从表6的回归结果可以看到，四个模型的核心解释变量ln(digital)的系数都为正，且都通过了显著性检验。对模型进行豪斯曼检验，检验结果显示chi2(7)=48.08，P=0.000，拒绝使用随机效应模型的原假设，应使用固定效应模型。拟合优度方面，双向固定效应模型的拟合优度要更好，达到了0.7324，同时考虑到数字经济对农业的促进作用可能存在着不随个体而随时间变化的遗漏变量或不可观测因素，本文最终选择了更为合适的双向固定效应模型。因此，以下将使用表6列（3）的双向固定效应模型的估计结果进行分析。

表6 数字经济发展水平与全要素生产率的回归结果

双向固定效应模型估计结果显示，ln(digital)的估计系数为0.1737，表明数字经济的发展对农业全要素生产率的提高有促进作用，且具体表现在数字经济发展水平每提高1%，农业全要素生产率提高0.1737%。

在控制变量方面，经济发展水平的系数、自然灾害的系数没有通过显著性检验，说明地区经济发展水平与自然灾害对农业发展没有实质性影响；工业化程度的系数为负，且通过显著性检验，说明地区的工业化程度对该地区的农业发展有着抑制作用；财政支农力度的系数为正，且通过显著性检验，说明政府财政支持有助于农业发展；农业结构调整的系数没有通过显著性检验，说明其对农业发展没有实质性的影响。

2.4 估计结果的稳健性检验

为了估计的可靠性，选用了工具变量回归法和替换被解释变量两种方法进行估计结果的稳健性检验。

（1）工具变量回归法

考虑到数字经济发展水平与全要素生产率之间可能存在的内生性问题，因此选择滞后一期的数字经济发展水平作为工具变量，采用两阶段最小二乘法（2SLS）重新估计模型，估计结果如表7所示。

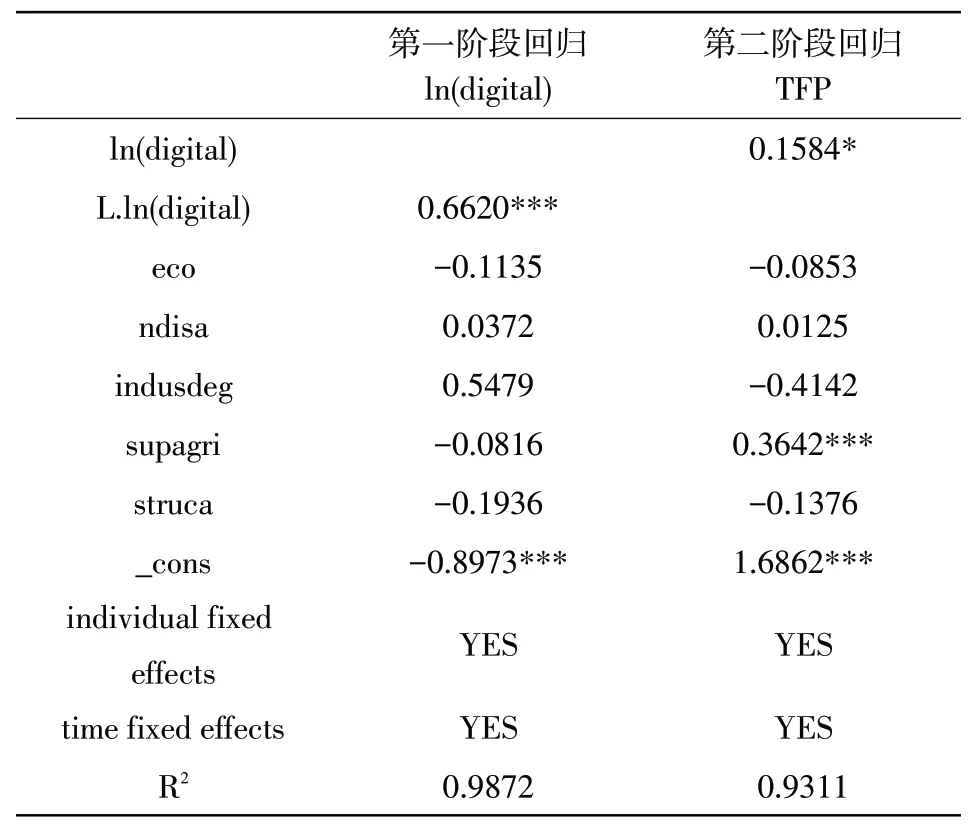
表7 2SLS的估计结果

第一阶段的回归结果表明，解释变量与工具变量有显著的正相关关系，R2为0.9872，说明滞后一期的数字经济发展水平作为工具变量是合适的。第二阶段的回归结果表明，数字经济发展水平与全要素生产率显著正相关，表明双向固定效应模型的估计结果具有稳健性。

（2）替换被解释变量

用索罗余值法测算的全要素生产率（tfp3）替换被解释变量，利用原回归模型进行参数估计，回归结果如表8所示。数字经济发展水平的系数为正，且通过了显著性检验，说明数字经济发展水平对农业发展仍有促进作用，因此该回归模型具有稳健性。

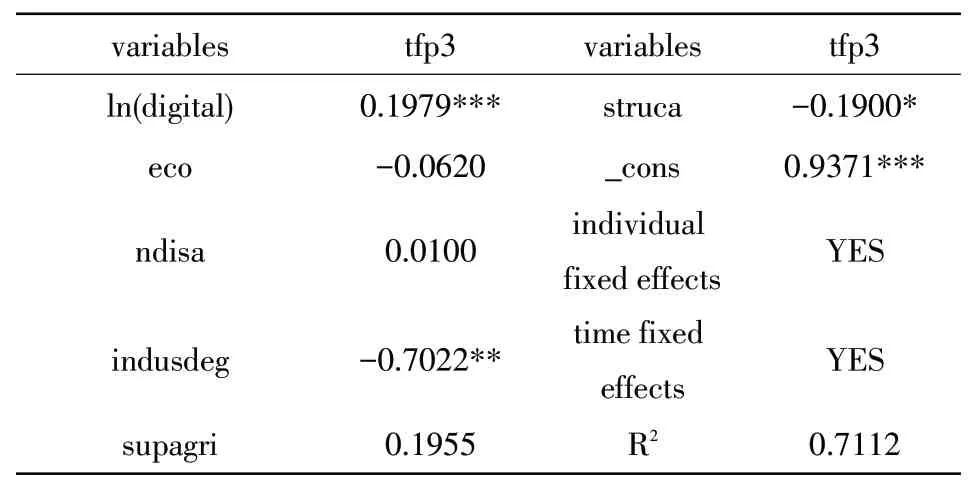
表8 稳健性检验

3 结论与建议

3.1 结论

从农业农村角度来看，数字经济发展水平相对来说并没有发挥优势，这很大程度上取决于地区的主导产业、政府关联度以及数字化农业人才引入等。突出表现为西南地区的显著正向推动作用，西南地区主要包括云南、贵州、四川等地，该地区的农业数字经济发展水平在全国属于中间水平，农业全要素生产率更多地处在第一梯队，该地区在数字基础设施和数字化产业的交易等方面表现出一定的突出性，且很大程度上作用在农业全要素生产率的提高上，说明数字经济对于推动农业全要素生产率具有强大的赋能效果和潜力，但华北地区呈现出一定的负向作用，北京、河北、天津等地更注重制造业、工业等，数字经济的提升速度低于农业全要素生产率的提升。东北地区、华北地区农业农村数字经济基础设施、产业发展以及数字化农业交易在推动农业全要素生产率方面稍落后于西南地区，仍保有很大的提升空间，因此需要更好地实现农业的数字化，将新的技术应用在农业生产中，发挥现代化的优势。

3.2 政策建议

持续加快数字基础设施的稳健保障，充分发挥数字经济优势。农业数字化基地建设、农产品的数字化交易等变量具有较高的权重，因此要不断地加快数字化基础设施建设，加快发展5G网络，应用物联网、互联网、大数据等信息技术到农业种植、农业生产中，借助数字基础设施的加持来加强农业生产、流通、销售各环节的数据信息的采集、分析，促进农业数字化发展，实现传统农业转型升级。

加大数字农业人才培养，多因素助力农业现代化进步。着力培养数字农业领域专业人才，当前具备农业产业和信息技术应用的复合型专业人才还比较紧缺，且受到工作环境以及薪酬等问题的制约，因此政府需要制定相应的优惠政策，鼓励大学生加入到基层农业的发展建设中，弥补农村数字化人才缺口。

深化工业支持，发挥潜在力量助力农业发展。数字经济对现代农业的发展有积极的促进作用，而工业化程度对农业全要素生产率却起着抑制作用，要助力工业与现代农业协调发展，地区工业的发展有助于为农业提供工业技术和工业产品，如农用设施、农用机械、化肥等，实现农业的现代化。因此应当发挥出工业对农业的促进作用，并避免在发展工业的同时，造成土地资源紧张、环境恶化等问题，抑制农业的发展，促进协调发展，此外需要在不同区域实行具有差异化的战略。