外场下一种分形上Potts模型的临界性质

尹训昌，马业万

（安庆师范大学，安徽 安庆 246133）

0 引言

相变在自然界中广泛存在，系统在相变点附近的临界性质一直是统计物理中的一个重要的研究课题，在汪志诚所著的《热力学与统计物理》的相变章节中，主要求得了在无外场时一维Ising系统和正方格子Ising模型的相变点。教材中的正方格子是平移对称晶格，即有平移对称不变性的特点。分形不满足平移对称特点，并且它具有一个有趣的特点，即分形维数可以取非正整数，更加接近自然界的真实铁磁系统，因此，研究分形上的相变和临界特性有一定的理论意义。分形最早在数学中提出，它具有自相似的特点，分岔度和分形维数是两个重要指标。上世纪80年代初，Gefen等最先研究了几种规则分形上Ising模型的相变［1］，求得了无外场下系统的相变点。从此以后，分形系统上自旋模型的相变成了一个研究热点［2-7］。Ising模型是一种最简单的自旋模型，可以模拟铁磁材料的相变，但自旋变量只能取1和-1两个值。而Potts模型的自旋变量可以取连续的整数值，能更好地解释铁磁材料的相变问题。Potts模型的工作主要集中在无外场情况下，不能很好地说明在相变点附近的临界行为。本文研究存在外场情况时的临界特性，采用实空间重整化群变换的方法，研究一种不能约化的分形上Potts模型的临界特性。

1 外场下一种分形上的Potts模型

本文研究的分形是一种规则分形，构造过程见参考文献［5］，它的分岔度为无穷大，其分形维数为d f=ln 8/ln 2=3。为了简单，只考虑最近邻相互作用，存在外场时该分形上2态Potts模型的有效哈密顿量表示为：

（1）式中，K表示约化的相互作用变量，si和sj分别代表分形格点i和j上2态Potts模型的自旋变量，si和sj取1和2两个数值，＜sisj＞表示对格点自旋的最近邻求和，δ是克罗内克delta符号，h代表简化的外磁场。此系统的配分函数为：

2 实空间重整化群过程

取该分形的生成元图1（a）进行重整化群变换，其格点上的自旋分别用sa，sb，s1，s2和s3来表示。根据表达式（1），可以写出生成元的有效哈密顿量为：

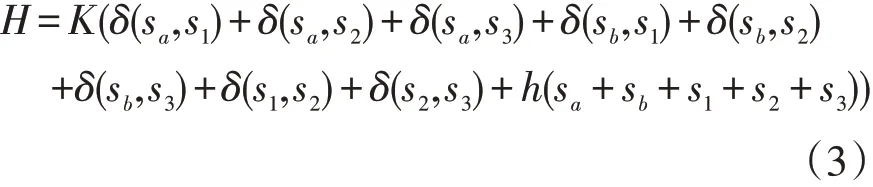
图1 实空间重整化群变换过程

经过实空间重整化群变换后，图1（a）内部的s1，s2和s3被消去变为图1（b），这个过程写为：

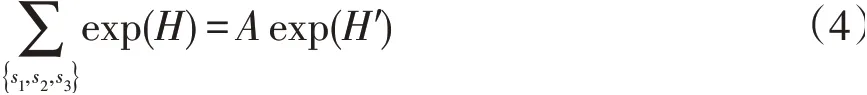
上式中，A仅表示一个与积分有关的重整化群变换常数，H′为一次重整化群变换后的有效哈密顿量，它的表达式写为

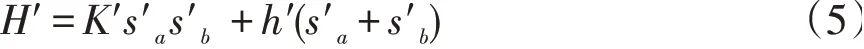
其中，s′a和s′b表示图1（b）格点位置上的自旋变量，K′表示图1（b）的最近邻的相互作用变量，h′表示重整化群变换后的简化的外磁场。

根据（3）式、（4）式和（5）式，经过计算，得到该系统重整化群变换后的表达式为：

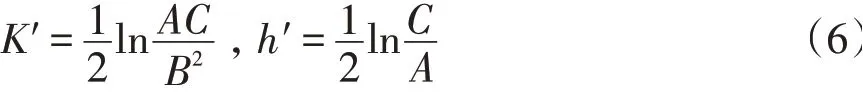
其中

（6）式称为该系统的递推关系。从（6）式出发，假设最近邻相互作用参数K′=K=K*，h′=h=h*，通过计算求得该系统的临界点为：

根据实空间重整化群变换理论，把递推关系（6）式在临界点处展开，得到该系统的线性变换矩阵如下：

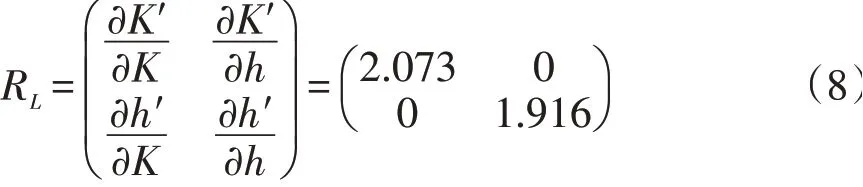
从（8）式很容易看出该矩阵的本征值为λ1=2.073，λ2=1.916，其中λ1是一个与温度有关的本征值，而本征值λ2则表示磁场有关的量。根据标度理论，由两个本征值得到标度幂如下：

其中，df=3表示该分形的分形维数，L=2表示变换的标度因子。用α、β和γ分别表示该系统的比热、自发磁化强度和零磁场磁化率的临界指数，而磁场强度、关联函数和关联长度的临界指数则依次用δ、η和ν表示。上面的6个临界指数可以很好地反映系统在临界点的临界特性，根据6个临界指数的定义式求得临界指数的值分别为α=-0.851，β=1.960，γ=-1.068，δ=0.455，η=3.124，ν=0.950。

3 结论

应用重整化群变换的方法，讨论了外场下一种分形上Potts模型的临界行为，得到了该系统的临界点和6个临界指数。结果表明，该分形加上外场后，系统在在K*=0.528，h*=0发生相变，即存在有限温度的相变。与外场下该分形上的Ising模型相比较，发现两个系统都存在有限温度的相变，但临界点和临界指数的数值发生了改变，究其原因是它们属于两个不同的物理模型。通过分析，发现它们属于不同的普适类。