基于2021年中考“方程与不等式”专题复习作业的设计*

⦿广东省中山市东区远洋学校初中部 麦雄军

2021年各省市中考数学对方程与不等式的考查重点在于熟练掌握基础知识和基本运算技能，侧重于以当代实际生活为背景的问题解决，落实“以德树人”的根本任务.2021年7月下旬，中办、国办印发的《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》(简称“双减”政策)，对作业提出了“发挥作业诊断、巩固、学情分析等功能，将作业设计纳入教研体系……”新的要求.这意味着教师要设计高质量且符合学情的作业，彻底减轻学生的负担.笔者基于2021年各省市中考数学试题的研究，围绕“方程与不等式”专题复习进行作业设计.

1 作业设计目标

通过作业，达成下列目标：

(1)复习和巩固“方程与不等式”相关基础知识，知道一元一次方程、二元一次方程组、一元二次方程、分式方程、一元一次不等式(组)的解法.

(2)领悟转化、数形结合、数学模型、方程等数学思想，构建知识之间的联系.

(3)学会解决相关综合问题，提升分析问题、发现问题、解决问题的能力.

2 作业设计内容

2.1 夯实基础，实施有效训练

图1

答案：C.

(3) (2021·吉林长春)关于x的一元二次方程x2-6x+m=0有两个不相等的实数根，则m的值可能是( ).

A．8 B．9 C．10 D．11

答案：A.

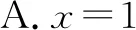
答案：D.

设计意图:作业(1)回顾了二元一次方程组的基本解法，可以采用代入消元法和加减消元法；作业(2)考查了一元一次不等式组的解法，借助数轴来理解不等式组的解集；作业(3)考查了一元二次方程根与判别式之间的关系；作业(4)考查了分式方程的解法.通过本环节的作业设计，这些基础知识和基本技能将为下一阶段的学习作好铺垫.

2.2 积累经验，活用思想方法

答案：3

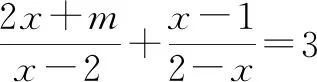
答案:m>-7且m≠-3.

(7) (2021·四川自贡)已知x2-3x-12=0，则代数式-3x2+9x+5的值是( ).

A.31 B. -31 C. 41 D.-41

答案:B

(8)(2021·湖北鄂州)数形结合是解决数学问题常用的思想方法．如图2，直线y=2x-1与直线y=kx+b(k≠0)相交于点P(2，3)．根据图象可知，关于x的不等式2x-1>kx+b的解集是( ).

图2

A．x<2 B．x<3 C．x>2 D．x>3

答案：C.

设计意图：对于作业(5)中一元一次方程涉及的参数，只要抓住一元一次方程的概念，这道题便迎刃而解.作业(6)涉及分式方程的解法，把分式方程转化为整式方程时，容易忽略分母不能为0；本题渗透了转化的数学思想，以让学生灵活掌握分式方程的解法.作业(7)渗透了整体的数学思想，通过转化和整体代入解决数学问题.作业(8)渗透了数形结合的数学思想，通过图形来直观得到不等式的解集，抓住数学本质，积累解题经验，达到“事半功倍”的效果.

2.3 注重综合，发展数学能力

(9)(2021·湖南株洲)《九章算术》之“粟米篇”中记载了中国古代的“粟米之法”：“粟率五十，粝米三十……”(粟指带壳的谷子，粝米指糙米)，其意为：“50单位的粟，可换得30单位的粝米……”．问题：有3斗的粟(1斗=10升)，若按照此“粟米之法”，则可以换得的粝米为( ).

A．1.8升 B．16升

C．18升 D．50升

故选：C．

设计意图：本题旨在考查学生的阅卷理解能力，渗透数学史.本题难在用正确的数学语言表达数学问题，列出分式方程，并转化单位.

(10)(2021·江苏连云港)为了做好防疫工作，学校准备购进一批消毒液．已知2瓶A型消毒液和3瓶B型消毒液共需41元，5瓶A型消毒液和2瓶B型消毒液共需53元．

(ⅰ)这两种消毒液的单价各是多少元？

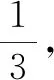
解析：(ⅰ)设A种消毒液的单价是x元，B型消毒液的单价是y元．

所以A型消毒液的单价是7元，B型消毒液的单价是9元．

(ⅱ)设购进A型消毒液a瓶，则购进B型(90-a)瓶，购买总费用为W元．

所以，当a=67时，最少费用为810-2×67=676元，此时，90-67=23．最省钱的购买方案是购进A种消毒液67瓶，购进B种23瓶．

设计意图：本题是一道关于二元一次方程组、一元一次不等式、一次函数性质的综合题，第(ⅰ)问也可以用一元一次方程来解答.旨在考查学生运用方程和不等式等数学知识解决生活中的实际问题，把实际问题转化为数学问题的能力.在数学建模的过程中，提升学生发现问题、分析问题、解决问题的能力，并注重运算能力的培养，发展学生核心素养.

3 作业设计建议

3.1 作业设计应以核心素养为目标

在新时代背景下，数学教育的发展目标是提升学生数学素养.作业设计始终要以发展学生的核心素养为目标，不能盲目搞“题海战术”，作业设计的练习不宜多，应给与学生充分思考的时间.设计的作业要让学生经历定理、概念的习得过程，注重学生数学抽象、逻辑推理等核心素养的培养；借助几何直观，渗透数形结合、转化等数学思想，培养学生的直观想象能力；注重学生运算能力、数学建模等核心素养的培养.总之，要把发展学生的核心素养落实到作业中.

3.2 作业设计应注重整体性

“双减”政策要求“坚决克服机械、无效作业，杜绝重复性、惩罚性作业”，设计高质量作业的途径之一就是从整体视角下开展教学.《义务教育数学课程标准(2011年版)》(以下简称《标准》)指出：“数学知识的教学，要注重知识的‘生长点’与‘延伸点’，把每堂课教学的知识置于整体知识的体系中，注重知识的结构和体系，处理好局部知识与整体知识的关系，引导学生感受数学的整体性.”[1]作业设计要从整体的角度出发，作业设计内容要体现整体性，基于《标准》和教材，以作业为载体，把数学知识之间的联系有机融合，构建知识体系，提升学生数学思维，在问题解决中提升教育教学质量，实现高效作业.

3.3 作业设计应体现发展性

《标准》)指出：“教师教学应该以学生的认知发展水平和已有的经验为基础，面向全体学生，注重启发式和因材施教.”[1]作业设计要体现层次性和发展性，从学生最近发展区出发，基于学生的知识经验开展作业设计，避免出现偏题、怪题、难题，设计的内容由浅入深，环环相扣，由易到难，注重基础知识和基本技能的掌握、数学思想的渗透、基本的数学活动经验的积累，以“促进学生终身发展”为目标，落实“以德树人”的根本任务.

3.4 作业设计内容应注重综合性与情境性

《标准》)指出：“在注重对基础知识和基本技能考查的同时，特别重视对具体情境中综合运用知识分析和解决问题能力以及实践能力的考查.”[1]作业设计内容要注重综合性和情境性，让学生体会数学来源于生活而又服务于生活.精选习题，精心设计情境性数学问题，让学生在问题解决的过程中，体会数学的应用价值，提升学生的思维能力、实践能力和解决实际生活问题的能力，发展学生的创新思维， 促进学生全面发展.