一种纵、横向视野不同的编码孔径伽玛相机的方法论述与模拟验证
李 岩,刘立业,曹勤剑,赵 原,夏三强,董佳杰
(中国辐射防护研究院,太原 030006)
射线成像技术是核辐射探测领域的新技术,能够远距离探测到视野范围内的放射性物质以及给出二维分布图像,并配合光学摄像头直观地指示热点位置[1]。根据探测到的射线能谱,可以进行核素识别进而确定放射性物质的类别[2]。编码孔径成像技术通过准直方法(特定图样的多开孔准直器)可以快速定位到放射源的位置,广泛应用于宇宙空间探测、辐射环境监测以及核应急等领域,已经成为现今重要的射线成像技术之一[3-5]。目前较为主流的编码方式,如均匀冗余阵列(uniformly redundant arrays,URA)[6]或者修正均匀冗余阵列(modified uniformly redundant arrays,MURA)[7]都要求纵横向视野近似相同或者相同,然而在某些实际的应用中往往是纵向视野在较小的情况下就可以将物体完全包含在内,横向视野越大对整个系统越好,如对核电厂内管道源项位置的测量。这两种编码方式都无法自支持(self-supporting)[8],需要额外的机械结构进行固定,这导致在进行活性准直时(active collimation)时难以制造。如图1所示,可以看出红线画出的实体部分处于悬空的状态,整体的编码准直器没有办法进行自支持。为解决现有的基于URA或者MURA编码方式的编码孔径伽玛相机纵、横向视野必须相同以及无法自支持的问题,提出了使用纵向和横向编码序数可以不同的且具有自支持能力的M-M编码方式来制作编码孔径伽玛相机的编码准直器[9]。该种灵活的纵、横向编码序列数可以按照实际的需求,灵活地进行设置,以满足纵横向的视野要求并且提高成像角分辨率,而且其自支持特征也使其免于复杂的机械固定。本文通过蒙特卡罗模拟方法,使用不同能量的放射源对不同厚度M-M编码准直器进行模拟计算,并对获取的重建图像进行分析对比,最终确定最佳编码准直器厚度。对整个成像系统进行了多种类型的辐射场景的成像模拟,分析其成像结果。

图1 编码准直器(黑色和白色分别代表实体阻挡和透射)
1 基于M-M的编码孔径成像理论
编码孔径成像过程可以分为编码投影以及解码重建两个过程[10],如图2所示。以小孔为基本单位,对于每一个小孔都会得到一个放射源倒立的图像,这样探测器上会有许多个倒立的图像进行叠加形成叠加像,即编码过程。针对码板的编码方式可设计相应的解码重建算法,将探测器的投影图经过解码重建恢复放射源的图像,即解码过程。相较于针孔成像合理地增加开孔数目可以提高射线的透过率,从而提高系统的信噪比(signal to noise ratio, SNR)和灵敏度。
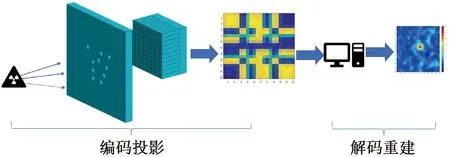
图2 编码孔径成像过程
编码孔径技术利用射线沿直线传播的特性,可以通过成像系统的几何分布进一步分析。假设码板为理想码板,即不计码板厚度,开孔位置射线透过率为100%,不开孔位置射线完全被阻挡。用O表示放射源强度分布函数,A为编码码板透过率函数,R表示探测器探测到的计数,本底噪声为N,则有式:
R=O*A+N
(1)
其中*表示卷积,如前面所述,解码过程是在探测器投影R的基础上进行的,如果针对所使用的编码函数A找到一个解码矩阵函数G使得:
A*G=δ
(2)
其中δ为冲激函数,即该编码方式具有理想的特性,不存在波动的旁瓣。将式(1)分别乘上解码矩阵函数G:
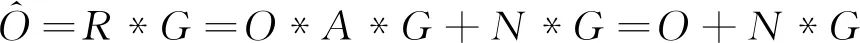
(3)

M-M编码与伪随机编码(pseudo-noise product,PNP)[11]的二维编码矩阵构造方式近似相同,M(i)与M(j)代表M编码序列,该一维矩阵中的数值为0或者1,其对应的序列长度分别为p和q,数值可以相同也可以不同,MURA的长宽维度数必须相同,因此可以非常灵活设计纵横向的成像视野(filed of view,FOV),M-M阵列由以下公式定义:
MM(i,j)=M(i)×M(j),
i=0,1,…,p-1,j=0,1,…,q-1
(4)
该编码方式的点扩展函数为δ函数,是一种理想的编码方式。由于p和q只能为素数,且矩阵数值为1的个数为(p-1)/2和(q-1)/2。MM(i,j)中0代表实体阻挡,1代表空白透射,从式(4)中可以得知无法实现25%的开孔率,随着像素数的增加,其开孔率无限逼近25%(开孔数与总像素数的比值称为开孔率),相比较MURA或者URA的50%较小,因此其成像灵敏度略逊,但是其对形状源的成像效果更好。
对于编码孔径系统所获取的图像,通常使用信噪比(signal-to-noise ratio,SNR)来定量判断成像质量,其中SNR由以下公式得到[12]:
(5)
式中,Nmax为重建图像像素中最大的数值;Nmean为除去放射源像素的背景像素平均值;Nbk为背景像素平均值的总像素数;Nij为除去放射源像素的背景像素数值。在本文中,当像素数值小于最大值的二分之一时,才会被认为是背景值,不然会被排除在外。
2 探测系统的设计
探测系统是编码孔径伽玛成像系统的核心部件之一,由编码准直器与位置灵敏探测器组成。而探测系统的具体设计直接决定了整个成像系统的角分辨率、SNR、FOV等重要指标。
2.1 基于M-M编码的初步准直器设计
编码准直器的设计主要包括编码阶数的选择、码板基本单元像素尺寸、码板厚度以及原材料组成等。
编码阶数的选择需要从整个系统的成像要求来进行选择,当编码阶数较大时,对于码板的加工、制造和位置灵敏探测器的要求都很高。理论上说,M-M编码方式的纵横编码阶数可以自由选择任意两个满足4m+1的素数。考虑到实际应用中位置灵敏探测器的像素限制,最终选择了编码阶数为13×17的原始矩阵,经过循环嵌套后,如图3所示,得到一个26×34阵列,然后将第一行和第一列删掉即可得到循环嵌套矩阵(25×33),获得的码板总共为25×33个基本单元。图3中红色部分代表编码准直器中的透射部分,即编码孔,在编码矩阵中为1,蓝色部分代表编码准直器的实体阻挡部分,在编码矩阵中为0。在模拟过程中,暂定初始编码准直器的基本单元尺寸为10 mm×10 mm×4 mm,厚度需要进行更为精细的模拟。使用的材料为金属钨(W),它的原子序数高,密度大,对γ射线的阻挡本领强。通过调研发现一种钨镍铜合金应用居多,其中钨含量(质量占比)为76%,镍含量为9%,铜含量为15%,该物质的密度为16.8 g/cm3。由于完整的编码投影才能进行图像重建,在横向视野有17个不同的完整的编码投影,其最佳角分辨率即为1/17,纵向视野有13个不同的完整的编码投影,其最佳角分辨率即为1/13。

图3 M-M编码阵列
2.2 位置灵敏探测器的设计
在成像系统中,探测晶体类别的选择至关重要。探测器材料选择的是一种名为GAGG(Ce)的淡黄色晶体[13-14],该晶体除了具有光产额高、较高能量分辨率、发光衰减时间短、高密度、无自发放射性以及较大原子序数等特点之外,还具有不潮解和易于生长等特点,这对于制作大阵列型位置灵敏探测器非常重要。在确定了编码准直器的阵列数和基本单元尺寸以后,位置灵敏型探测器的阵列也基本确定下来,一般是编码准直器的整数倍,而其长宽维度的整体尺寸与基础编码准直器相同。探测器阵列选择的是13×17,单根晶体条的尺寸为9.8 mm×9.8 mm×10 mm,晶体条之间使用氧化钛(TiO2)作为反射层,厚度为0.2 mm,所以整体的单根晶体条的“尺寸”为10 mm×10 mm×10 mm,整体的探测器阵列尺寸为170 mm×130 mm,如图4所示。

图4 探测器阵列平面图以及单像素结构
编码准直器和探测器阵列之间的距离(探测器前端面和编码准直器前端面的距离)是14.5 cm,横向视野大约为56°,纵向视野大约为42°。如图5所示,编码准直器和探测器的尺寸大小以及距离就决定了整个系统的FOV。
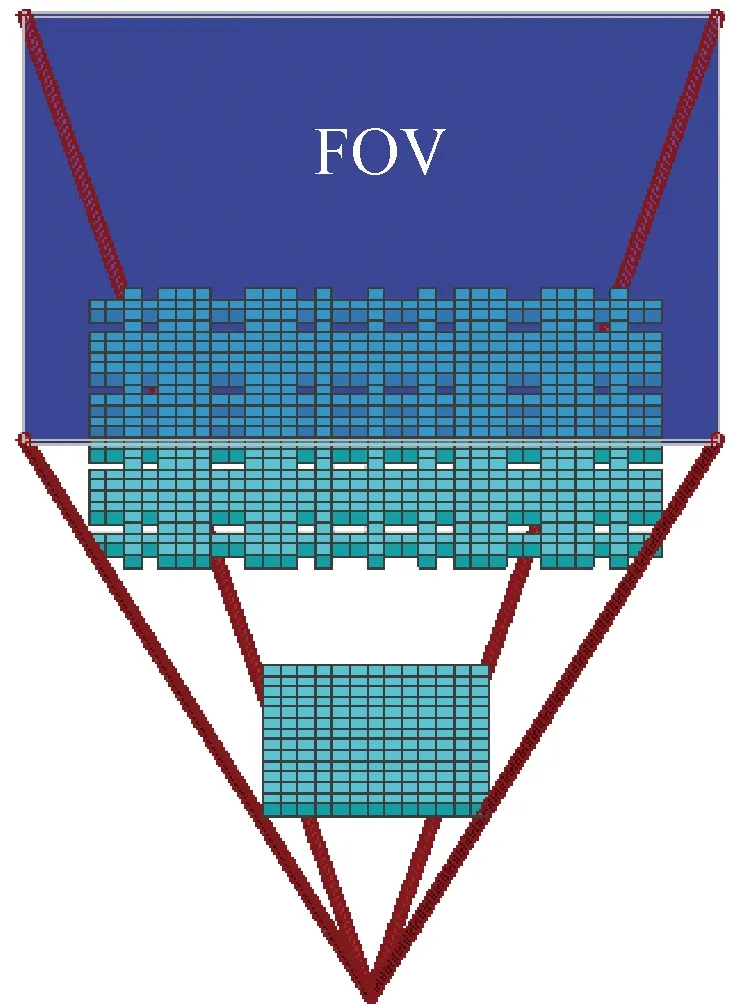
图5 编码孔径成像系统视野范围
2.3 编码准直器最佳厚度的模拟
确定了探测器和编码准直器的像素数、尺寸和两者之间的距离,角分辨率和FOV随之确定,但是编码准直器的厚度还未确定,该参数对成像系统重量以及重建图像质量存在较大影响。如果厚度较厚,会导致整个系统过重且会带来准直效应降低成像质量。而如果编码准直器的厚度较小的话,会导致较多的射线穿透准直器,起不到准值的效果或者效果很差,降低成像的SNR,因此通过模拟的手段最终确定编码准直器的厚度。使用MCNP5蒙特卡罗模拟软件,对不同能量的放射源,在不同的位置对不同厚度(4,6,8,10,12,15 mm)的编码准直器进行模拟仿真照射,通过对比各个参数下获取的重建图像的SNR来确定码板的最佳厚度。各个能量放射源(60 keV、356 keV、661 keV、834 keV)的模拟计算输入条件列于表1,其中放射源的不同位置仅仅是X轴的位置不同,Y轴和Z轴的坐标分别固定为0和500 cm(探测器阵列的中心为坐标原点)。放射源在X轴不同的位置,对应不同的成像角度(例如放射源在X轴157 cm时,对应成像系统的视野角度为17°)。最终获取的各个参数下的重建图像的SNR,如图6所示。

表1 各个能量放射源不同位置模拟计算输入条件

图6 在不同放射源的情况下,不同编码准直器厚度对成像质量的影响
从图6中可以看出,当放射源的能量较低时,其编码准直器的厚度对于成像质量的影响较小,而随着能量的增高,编码准直器的厚度对成像质量的影响也越大。这是由于能量较小时,即使编码准直器的厚度较小也可以阻挡大部分的射线,因此不会有较多透射过去的γ射线影响成像质量(噪声数据)。而随着能量的增高较薄的码板使得大部分的射线透过了编码准直器,没有起到准直效果,探测器投影的对比度较差,因此导致成像质量的下降。例如对Cs-137放射源,当其位置在0°时,编码准直器厚度为10 mm所获取的重建图像SNR是4 mm的1.33倍。从对较高能γ射线的成像SNR可以看出,当准直器的厚度超过10 mm以后,再继续增大编码准直器的厚度,其成像质量也不会获得明显的提高。
图6中SNR与角度的关系呈现出类似“锯齿状”,这主要是因为放射源的位置不同,由放射源所发出的γ射线透过编码准直器投影到探测器上的投影不同,如果编码准直器和探测器像素恰好相对,则SNR会较高,否则就会较差。编码准直器的厚度越厚,其相邻位置的成像SNR差距越大,这是因为编码准直器越厚,其投影的均匀性就越差,进而导致编码准直器和探测器像素恰好对应时,成像质量较好,而稍有偏离就会导致成像质量下降。
综上所述,为了保证对高能伽玛射线的成像质量,以及兼顾整体系统的重量且不会产生准直效应的考虑,将编码准直器的最佳厚度定为10 mm。
3 对点源和形状源成像结果与讨论
以上过程确定了探测系统的各个参数,其中编码准直器阵列为25×33,单像素为10 mm×10 mm×10 mm;探测器阵列为13×17,单像素尺寸为10 mm×10 mm×10 mm;探测器前端面和编码准直器前端面的距离为14.5 cm。后续对该编码方式进行了多种场景的放射源成像模拟,其中包括单点源、多点源以及形状源。点源(Cs-137)成像结果如图7所示。
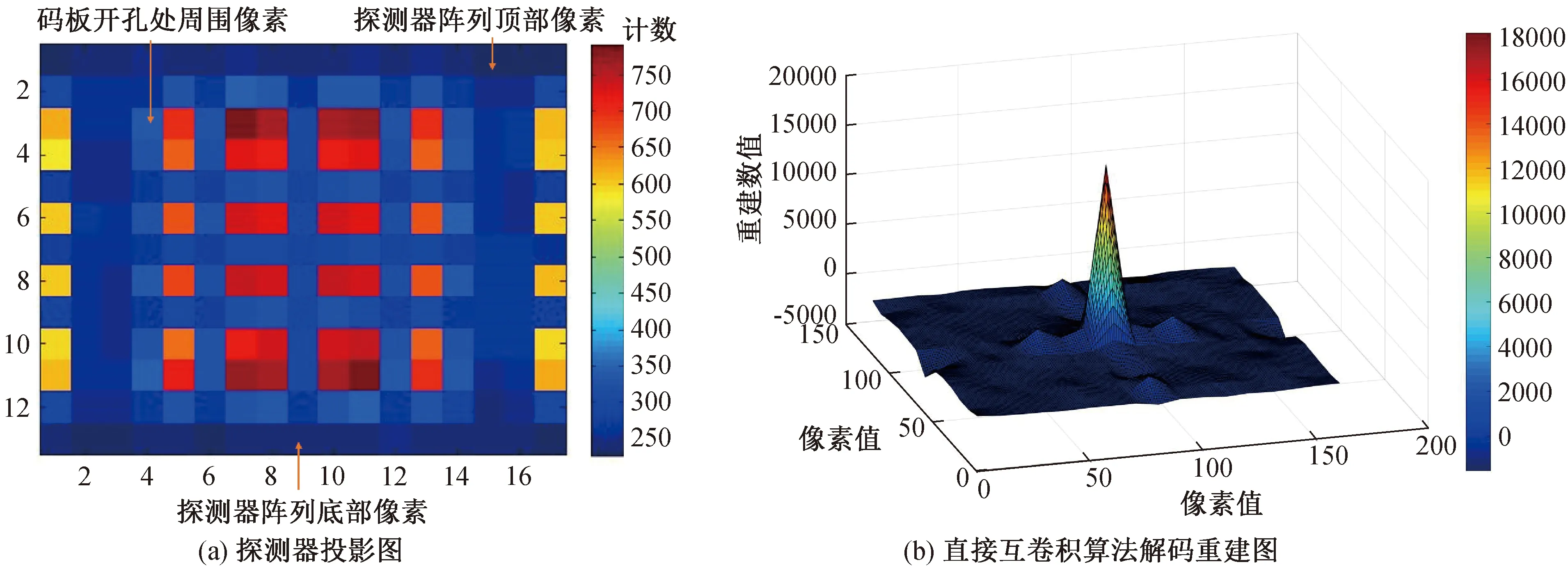
图7 成像系统对于单点源的成像情况
从投影图7(a)中可以看出,在编码准直器开孔处周围的像素相比较顶部和底部的探测器像素计数较大(模拟的总粒子数为108个)。这是因为伽玛射线的出射方向各向同性造成的,射线在穿过编码准直器开孔位置处时不是平行入射,导致开孔处周围的探测器像素计数也略有增大,这就是码板放大效应。不过这并不影响最终的重建图像,重建图像的SNR高达40.36。
角分辨率也是系统成像能力的一个重要指标。系统FOV的大小(即成像角度θ的大小)和所获得的重建图像的半高宽(full width at half maximum,FWHM)的大小决定了系统的角分辨率。由于视场θ是沿X轴方向定义的,故采用点源位于图像正中心时重建图像信号在X方向所占像素数作为FWHM,角分辨即可计算为:
(6)
式中N表示重建图像在X轴的总像素,这样定义的角分辨率表示相距为Δθ的两个点源,其重建的图像可以被分辨开来。对于Y方向上的角分辨率亦是如此,纵、横向视野上角分辨率分别为3.4°和3.3° (FWHM)。
图8是4个Cs-137点源成像的结果(模拟的总粒子数为109个)。从图8中可以看出,模拟的成像系统清晰地定位到4个Cs-137点源的位置,并且该系统完全分辨出这4个放射源,并没有较大的伪影出现,成像质量较高。
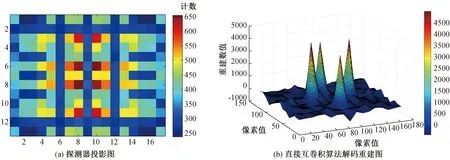
图8 成像系统对于多点源的成像情况
图9是一个圆桶状的形状源的成像结果(模拟的总粒子数为109个)。从图9可以看出,完全呈现出了形状源的一个形状,证明基于M-M编码方式的成像系统足够满足多种类型的放射源成像需求。

图9 成像系统对于形状源的成像情况
从以上三种类型放射源的成像效果来看,该系统均可以成功定位到放射源的位置,并且成像质量很高,说明M-M编码可应用于后期的实际编码孔径伽玛相机的研制。
4 结论
为了解决如今主流编码方式(如MURA或URA)纵横向视野不同以及无法自支持的问题,提出了基于M-M编码方式构建编码孔径伽马相机的编码准直器。本文通过蒙特卡罗程序MCNP对基于M-M编码方式的成像系统建立模型,使用不同能量的放射源在不同的位置,对不同厚度的编码准直器进行照射,通过分析重建图像SNR确定了最佳的码板厚度为10 mm。随后模拟了基于最佳码板参数的成像系统对单点源、多点源以及形状源的响应,并对重建图像进行了分析,其中单点源的重建图像SNR达到40.36。成像系统也成功重建出了形状源的形状,且背景没有波动的旁瓣。以上结果证明M-M编码方式优异的性能,具备代替MURA或者URA在特殊场景的应用潜力,本文可为后续的基于M-M编码方式的编码孔径伽玛相机的研制奠定基础。后续会开展基于M-M编码方式的多倍采样数成像系统模拟,判断多倍采样数对成像质量的影响。

