主被动异构弹载雷达组网抑制假目标干扰方法

韩晓斐， 何华锋， 何耀民， 周涛， 张琪， 张鑫

(火箭军工程大学 导弹工程学院， 陕西 西安 710025)

0 引言

现代战场环境中雷达导引头受到的电磁干扰愈加复杂，数字射频存储器(DRFM)作为电子干扰的发生器[1-4]可产生与真实目标回波特性高度相似的欺骗式假目标从而干扰雷达导引头对真实目标的识别，单部雷达导引头由于视角单一、信息量少，难以达到有效抑制假目标干扰的目的[5-11]。因此，可通过多个雷达导引头进行组网，协同抑制欺骗式假目标干扰。

针对组网雷达抗假目标欺骗式干扰的方法，可以根据融合信息的内容分为信号级融合抗干扰方法和数据级融合抗干扰方法[12-17]。数据级融合抗欺骗式干扰是将各站雷达中目标的点迹或航迹传输至融合中心，通过点迹关联、航迹关联对真假目标进行识别[18-19]。文献[20]根据真实目标具有空间一致性、假目标空间位置分散的特点提出了同源假设检验法。文献[21]利用位置信息和速度信息进行点迹融合鉴别假目标，该方法组网内至少有3部雷达才可实现基于速度信息的点迹融合。文献[22]实现了组网雷达对低可观测目标在欺骗干扰环境中的稳定跟踪。文献[23]在文献[22]的基础上增加了对杂波量测点剔除的方法，改进了目标滤波跟踪时最优量测输入点的寻找方法。以上文献都是同构雷达组网体制下基于真实目标具有空间位置相关性、非协同假目标不具备此特性的真假目标差异，在集中式融合结构中利用点迹信息抑制假目标干扰。

对于协同式欺骗干扰假目标，由于其同样具有空间位置相关性，无法使用同构雷达组网进行抗干扰处理，因此需要使用异构雷达组网对假目标进行鉴别[24]。文献[25]利用两坐标和三坐标异构雷达组网，基于距离、方位角信息进行点迹融合实现真假目标鉴别。文献[26]提出了基于基准线最小距离法和三维分配算法的主/被动异构雷达组网抗假目标干扰方法。文献[27]利用主/被动雷达组网基于距离和方位角信息进行卡方检验鉴别真假目标。文献[28]提出一种分布式结构下的主/被动雷达抗假目标干扰方法，该方法在航迹起始阶段和稳定生成航迹阶段两次剔除假目标干扰，仿真结果证明了该方法可以有效鉴别欺骗式假目标，降低主/被动异构雷达组网的被欺骗概率。

以上所述文献均是基于地面组网雷达抗假目标干扰的方法研究，而对于多弹协同抗假目标干扰的研究鲜少见到公开发表的文献；在真实环境中，组网中各雷达导引头自身位置动态变化，弹体自身定位误差会影响组网抗干扰性能，在异地配置的主被动异构弹载雷达组网抑制假目标算法中需要考虑雷达位置误差对鉴别效果的影响；分布式融合结构的异构雷达组网剔除了部分未生成稳定航迹的点迹，因此其数据量较少、假目标欺骗效果较差；主/被动异构雷达组网系统具有可靠性高、抗干扰能力强的优点。基于以上分析，本文以信号处理阶段抗干扰效果欠佳、在数据处理阶段存在虚假目标为研究背景，结合弹载雷达组网自身特点，考虑雷达导引头位置误差，使用方位角、俯仰角信息构造检验统计量，在航迹起始阶段和航迹滤波跟踪阶段通过点迹关联和航迹关联达到分布式结构下主被动异构弹载雷达组网抑制假目标干扰的目的，通过仿真实验验证本文算法的有效性。

1 系统模型

弹载雷达组网系统由一部主动雷达导引头和一部被动雷达导引头组成，假设两部雷达导引头同时对同一区域进行探测。干扰机接收到主动雷达导引头的信号后延时转发，组网内雷达导引头接收到的回波信号既包括真实目标也包括假目标，敌方以此实现距离式欺骗干扰[29]。主被动弹载雷达组网系统如图1所示。

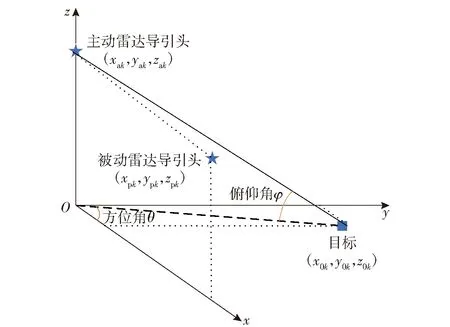
图1 主被动弹载雷达组网系统示意图Fig.1 Active/passive isomerism radar network

建立统一直角坐标系，主动雷达导引头在k时刻位置为(xak,yak,zak)，被动雷达导引头在k时刻位置为(xpk,ypk,zpk)，真实目标或自卫式干扰机在k时刻位置为(x0k,y0k,z0k)。

1.1 主动雷达导引头模型

主动雷达导引头的量测信息包括弹目距离rk、方位角θk和俯仰角φk，主动雷达导引头在k时刻的量测方程为

Za=[rk,θk,φk]T+ωk

(1)

式中：ωk为零均值的高斯白噪声序列，ωk～N(0,Ra)，

(2)

σr、σθ、σφ分别为主动雷达导引头的距离量测误差、方位角量测误差和俯仰角量测误差。

k时刻主动雷达导引头在直角坐标系下的位置误差方程为

Xa=[xk,yk,zk]T+δk

(3)

式中：δk为零均值的高斯白噪声序列，δk～N(0,RX)，

(4)

σax、σay、σaz分别为主动雷达导引头在x轴、y轴、z轴3个方向的位置误差。

1.2 被动雷达导引头模型

被动雷达导引头的量测量只包括方位角θ′k和俯仰角φ′k，被动雷达导引头在k时刻的量测方程为

Zp=[θ′k,φ′k]T+ω′k

(5)

式中：ω′k为零均值的高斯白噪声序列，ω′k～N(0,Rp)，

Rp=diag(σ′θ2,σ′φ2)

(6)

σ′θ、σ′φ分别为被动雷达导引头的方位角量测误差、俯仰角量测误差。

k时刻被动雷达导引头在直角坐标系下的位置误差方程为

Xp=[x′k,y′k,z′k]T+δ′k

(7)

式中：δ′k为零均值的高斯白噪声序列，δ′k～N(0,R′X)，

(8)

σpx、σpy、σpz分别为被动雷达导引头在x轴、y轴、z轴3个方向的位置误差。

1.3 距离欺骗干扰模型

假设无雷达量测噪声时，距离欺骗式假目标对于主动雷达导引头的量测值相当于在真实目标距离量测的基础上加上干扰机延时产生的欺骗距离，假目标在主动雷达导引头中的量测值为Z′a=[rk+Δrk,θk,φk]T，Δrk为欺骗距离。距离欺骗式假目标干扰模型如图2所示。

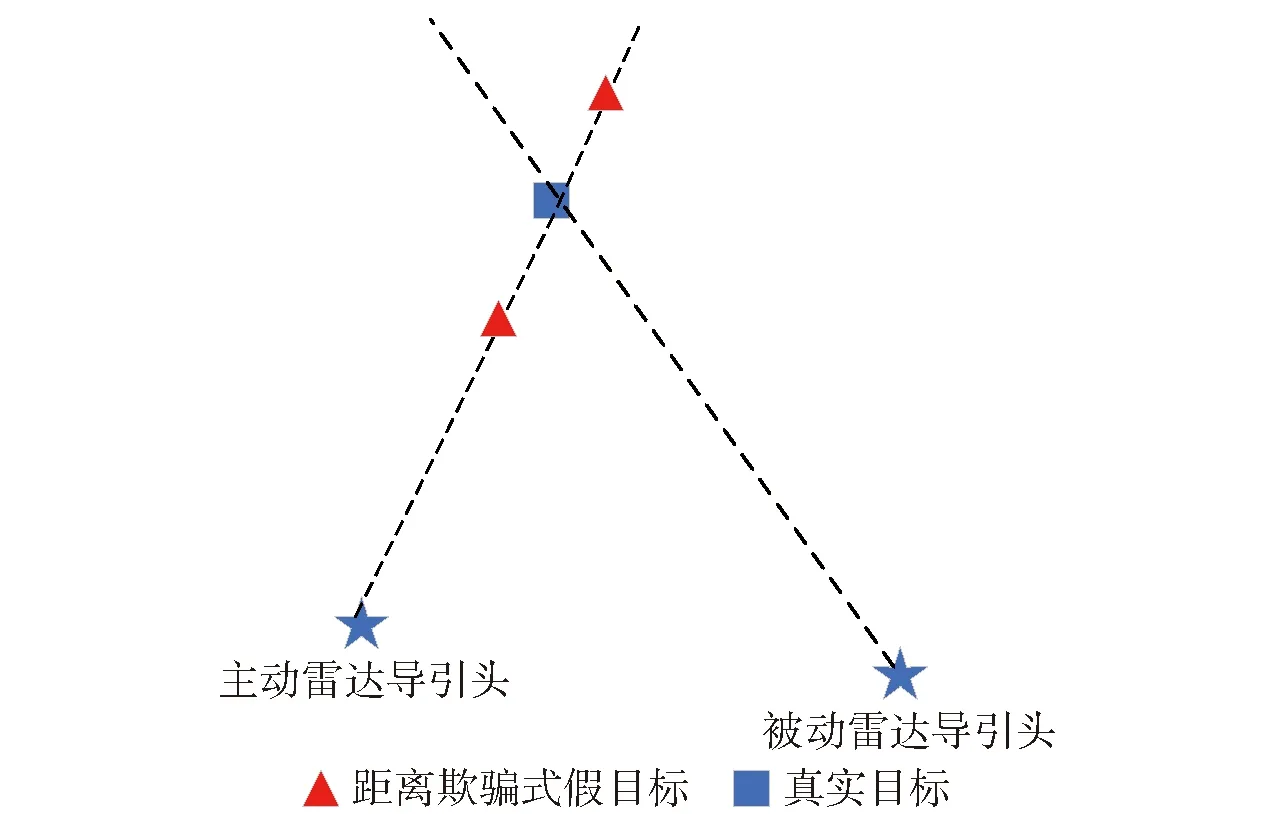
图2 距离欺骗式假目标干扰模型Fig.2 False-target jamming model based on deceptive distance

2 主被动异构弹载雷达组网抑制假目标方法

针对距离欺骗式假目标干扰，本文在分布式融合结构下采用主被动异构弹载雷达组网体制对欺骗干扰进行抑制，实现弹载雷达组网系统对真实目标的稳定跟踪。该算法在航迹起始阶段利用主动雷达导引头量测信息，估计出目标相对于被动雷达导引头的方位角、俯仰角信息，将估计信息与被动雷达导引头的量测信息进行假设检验，同时将主被动雷达导引头自身位置误差加入考虑，使得算法模型更加贴近真实环境。由于被动雷达导引头缺少距离量测信息，因此需要通过主动雷达的量测信息辅助被动雷达进行航迹起始、滤波跟踪。通过航迹起始阶段的假目标鉴别剔除掉部分距离真实目标较远的假目标，然后利用主动雷达导引头量测信息辅助被动雷达导引头进行航迹起始形成稳定航迹。最后将两部雷达导引头形成的稳定航迹进行序贯航迹关联再次鉴别假目标。主被动异构弹载雷达组网抗假目标干扰方法研究的总体思路如图3所示。

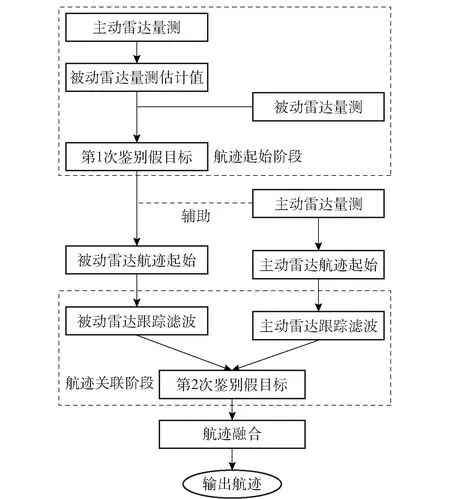
图3 主被动弹载雷达组网抑制假目标 干扰流程图Fig.3 A method against false-target jamming based on active/passive isomerism missile-borne radar network

主被动异构弹载雷达组网抑制假目标干扰主要分为3部分：航迹起始阶段考虑弹载雷达位置误差的真假目标鉴别、主被动异构弹载雷达分别航迹起始、航迹关联阶段真假目标鉴别。

2.1 考虑雷达位置误差的假目标鉴别方法

设主动雷达导引头在k时刻的位置为(xak,yak,zak)，将其量测值Zak=[rk,θk,φk]T转换至统一直角坐标系下：

(9)

根据主动雷达导引头在统一直角坐标系下的观测值，估计出目标相对于被动雷达导引头的方位角和俯仰角信息：

(10)

(11)

式中：

(12)

T为转换矩阵，通过对(10)式两边微分求得，

(13)

若主动雷达导引头与被动雷达导引头的量测对应于同一个目标，则目标相对于被动雷达导引头的估计值k与被动雷达导引头实际量测值Zpk=[θ′k,φ′k]T的差值εk=k-Zpk服从零均值、误差协方差为Σk的高斯分布。组网内两部雷达导引头量测误差不存在耦合，因此差值εk的误差协方差矩阵Σk=Qk+Λp，Λp=diag(σ′θ2,σ′φ2)。对估计值与被动雷达导引头实际量测值的差值进行假设检验：H0表示主动雷达导引头与被动雷达导引头的量测值对应于同一目标；H1表示主动雷达导引头与被动雷达导引头的量测值对应于不同目标。

在我国的税收的政策当中，除了规定了各行各业的缴税要求，也包含了一些缴税的优惠政策，如研究开发费优惠政策、综合利用资源的优惠以及增值税优惠等等。

利用估计值与被动雷达导引头实际量测值差值的马氏距离构造检验统计量，即

(14)

当H0成立时，dk服从自由度为2的卡方分布，因此对统计量进行卡方检验，假设检验问题转化为

(15)

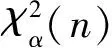
2.2 航迹起始阶段鉴别假目标

假设航迹起始阶段的时间为K，对考虑雷达位置误差假目标鉴别方法计算出的马氏距离在航迹起始阶段进行时间积累，则航迹起始阶段的检验统计量为

(16)

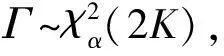
在航迹起始阶段鉴别假目标过程中，如果被动雷达导引头某一量测与主动雷达导引头多个量测同时关联成功时，为了避免主动雷达导引头量测信息辅助被动雷达导引头重复起始航迹，使用关联距离最小的主动雷达导引头量测信息辅助被动雷达导引头进行航迹起始。但是这种处理方式可能会错误使用主动雷达导引头的假目标量测信息辅助被动雷达导引头航迹起始，由于此时真假目标距离较近，因此被动雷达导引头可以使用该假目标量测信息进行航迹起始。

2.3 航迹关联鉴别假目标

在航迹起始阶段考虑雷达导引头位置误差的假目标鉴别算法可以尽可能保证真实目标不被剔除，并剔除掉部分欺骗距离较大的假目标，但是仍会有部分假目标通过检验形成稳定航迹，对此类假目标可以通过主被动异构弹载雷达航迹关联的方法进一步予以剔除。

利用卡尔曼滤波对组网内主动和被动雷达导引头的量测信息进行滤波跟踪，分别形成航迹。假设两部雷达导引头的航迹已经完成时空对准，选择进行航迹关联的状态总个数为M。在k时刻，主动雷达导引头的状态估计矢量为k，误差协方差矩阵为Pk，被动雷达导引头的状态估计矢量为′，误差协方差矩阵为P′k，即

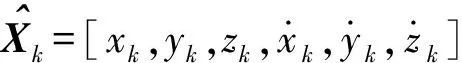
(17)

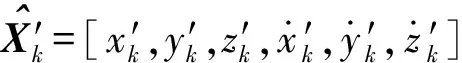
(18)

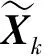
(19)

(20)

(21)

由于航迹关联的状态总个数为M，对单个状态估计矢量之差的马氏距离进行时间积累，得到两条航迹的关联假设检验统计量为

(22)

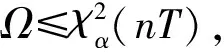
对主动雷达导引头与被动雷达导引头中的航迹进行两两关联后，在航迹关联结果中可能会存在一条航迹同时关联多条航迹的情况，选择关联距离最小的两条航迹进行后续的航迹融合处理，最终输出系统航迹。若在关联结果中，主动雷达导引头中某一航迹无与之关联成功的航迹，则将此航迹判定为假目标产生的虚假航迹并进行剔除。

3 仿真实验

根据第1节给出的主被动异构弹载雷达组网抑制假目标干扰系统模型进行参数初始化，如表1所示。在统一直角坐标系下只设置一个真实目标，其位置为(8 000 m，400 000 m, 0 m)，初始运动速度矢量为(0 m/s，10 m/s，0 m/s)。假设在观测时间内，目标和两部雷达导引头做匀速直线运动，观测时间间隔为0.1 s。进行5 000次蒙特卡洛仿真，定义真实目标鉴别概率为通过算法将真实目标判定为真目标的概率，假目标鉴别概率为将假目标判定为假目标的概率。

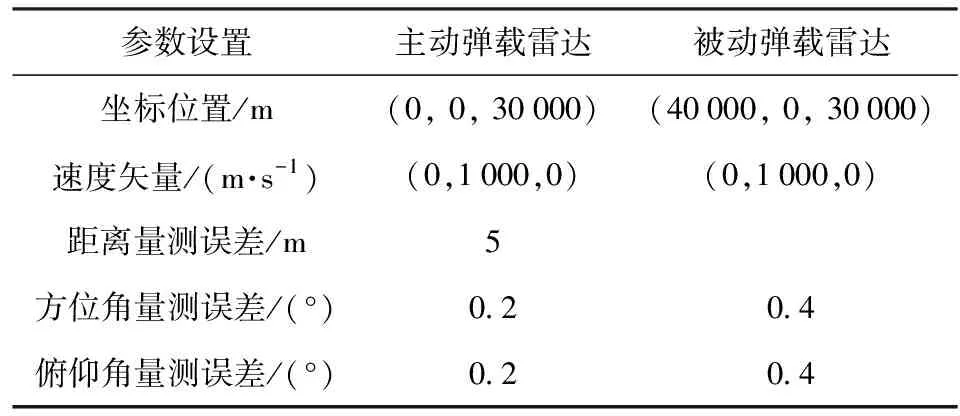
表1 参数初始化Table 1 Parameter initialization

3.1 雷达位置误差对鉴别概率的影响

设置假目标欺骗距离为1 500 m，航迹起始时间长度为0.5 s，将主动和被动弹载雷达自身位置误差由0 m增大到1 000 m，在航迹起始阶段分析其对真实目标鉴别概率和假目标鉴别概率的影响。图4为雷达位置误差对鉴别概率的影响。

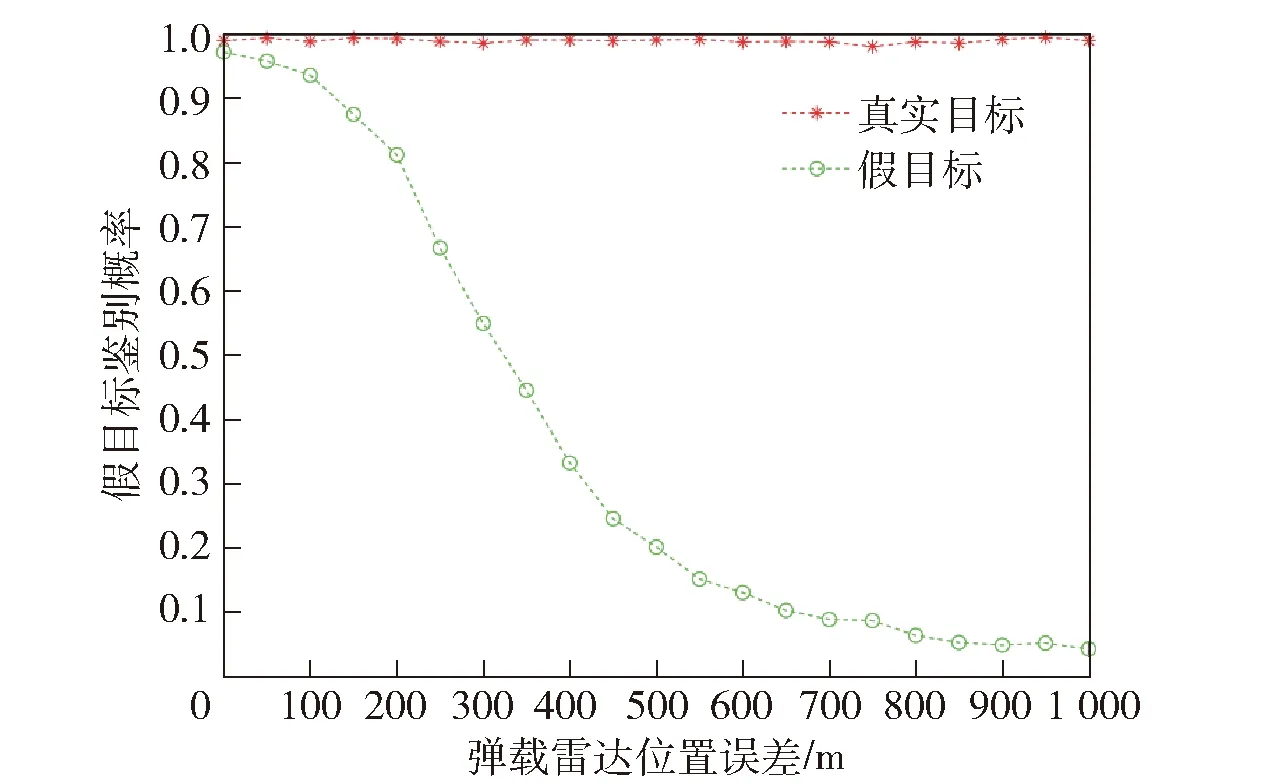
图4 雷达位置误差对鉴别概率的影响Fig.4 Effects of radar position error on discrimination probability

由图4可知，随着弹载雷达位置误差的增加，本文算法真实目标鉴别概率始终保持在较高水平，而假目标鉴别概率随着雷达位置误差的增大而降低。因此选择自身定位误差精确的弹载雷达进行组网可以有效提高组网系统对假目标的鉴别效果。

3.2 欺骗距离对鉴别概率的影响

设置欺骗距离由200 m逐渐增大到2 000 m，在航迹起始阶段对本文考虑雷达位置误差的算法与文献[28]算法进行对比，分析在弹载雷达位置误差分别为10 m、80 m、150 m的情况下，改变欺骗距离对于两种算法真假目标鉴别效果的影响，其余参数设置同3.1节。图5为欺骗距离对两种算法鉴别概率的影响。

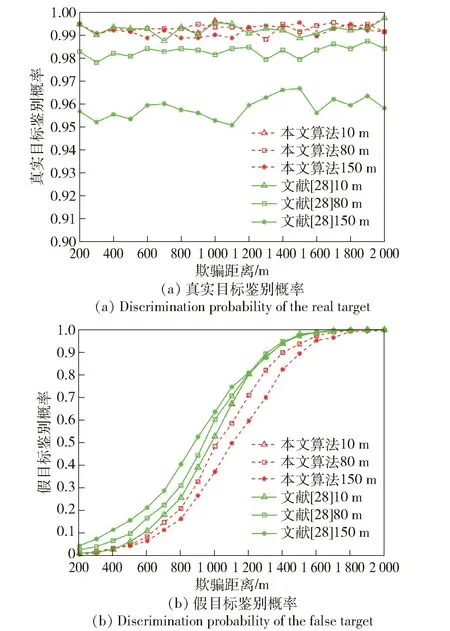
图5 欺骗距离对两种算法鉴别概率的影响Fig.5 Effects of deceptive distance on the discrimination probabilities of two algorithms

分析图5可知：

1)两种算法的真实目标鉴别概率随欺骗距离增大均保持稳定；假目标欺骗距离越大越容易被区分，因此两种算法的假目标鉴别概率均随之增大而增大。

2)由图5(a)可知，随着弹载雷达位置误差的增大，本文算法真实目标鉴别概率始终保持在较高水平，而文献[28]算法的真实目标鉴别概率受雷达位置误差增大的影响而逐渐降低。

3)由图5(b)可知，本文算法的假目标鉴别概率随着雷达位置误差的增大逐渐低于文献[28]算法。原因是文献[28]算法未考虑雷达位置误差，其误差协方差矩阵内的参数值低于实际情况，对误差协方差矩阵求逆后计算出的马氏距离反比增大，最终求得的马氏距离大于实际情况，难以通过卡方检验。因此，文献[28]算法的真实目标鉴别概率自然会低于本文考虑雷达位置误差的算法，其假目标鉴别概率同理略高于本文算法。

3.3 角度量测误差对鉴别概率的影响

设置假目标欺骗距离为2 000 m，被动雷达导引头的角度量测误差由0.1°增大至1°，在航迹起始阶段分析弹载雷达位置误差分别在50 m、100 m的情况下两种算法的真假目标鉴别效果。图6为被动雷达量测误差对两种算法鉴别概率的影响。

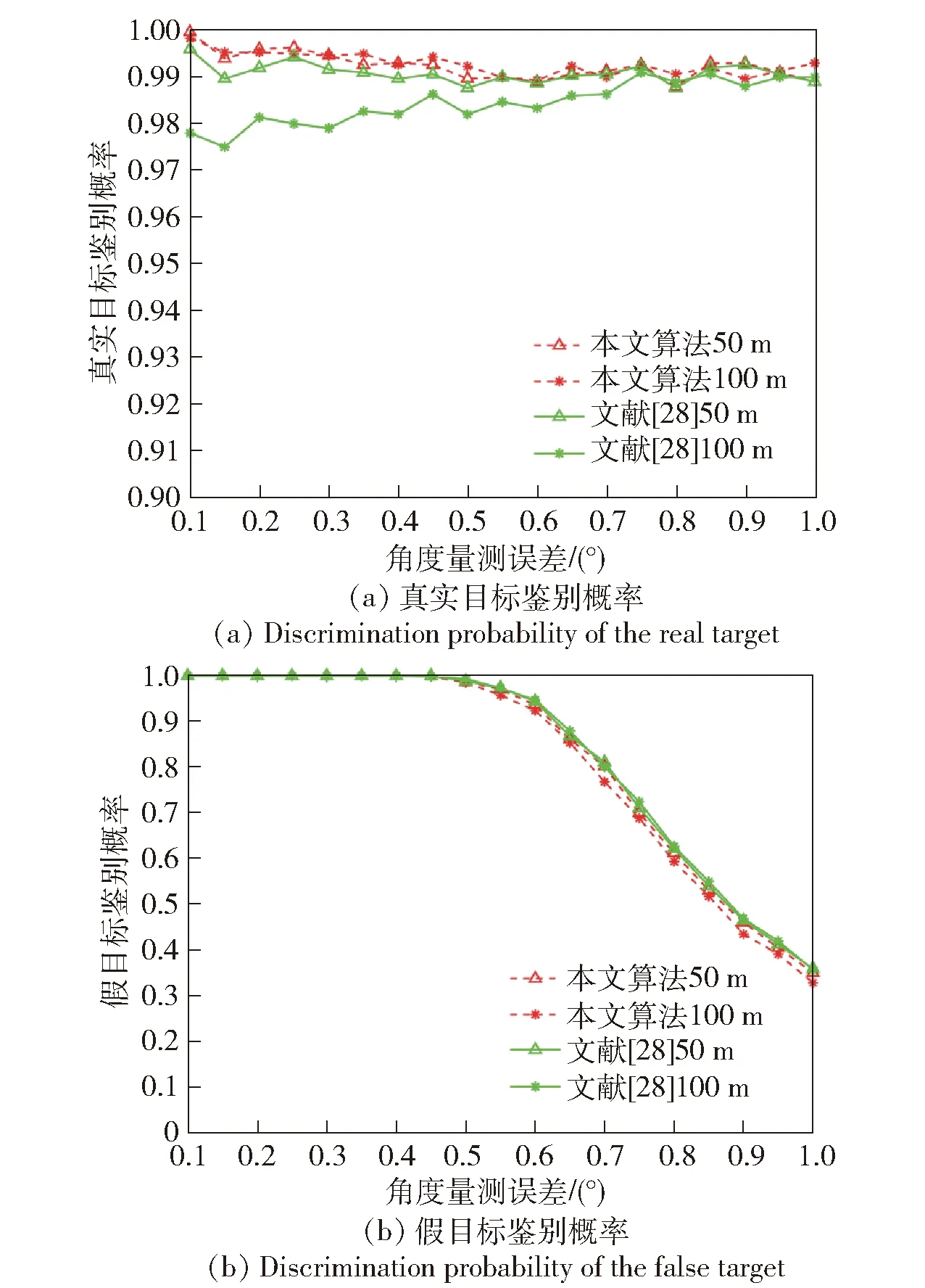
图6 被动雷达角度量测误差对两种算法鉴别概率的影响Fig.6 Effects of passive radar angle measurement error on the discrimination probabilities of two algorithms

由图6(a)可知，被动弹载雷达角度量测误差逐渐增大两种算法的真实目标鉴别概率均保持在较高水平，且本文方法的真实目标鉴别效果略优于文献[28]算法。

由图6(b)可知两种算法的假目标鉴别概率均随着被动弹载雷达导引头角度量测误差的增大而迅速降低。本文算法考虑雷达位置误差计算得到的马氏距离较小，因此其假目标鉴别概率略低于文献[28]算法，组网中选择自身定位精确的弹载雷达有助于提高假目标鉴别概率。

3.4 航迹起始时间对鉴别概率的影响

设置假目标欺骗距离为2 000 m，航迹起始时间从0.1 s增加至1 s，分析两部弹载雷达位置误差分别为50 m、100 m情况下航迹起始时间对两种算法真假目标鉴别概率的影响。图7为航迹起始时间对两种算法鉴别概率的影响。

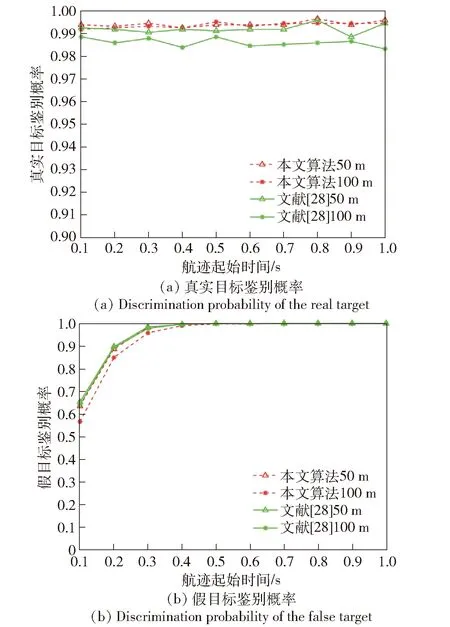
图7 航迹起始时间对两种算法鉴别概率的影响Fig.7 Effects of track initiation time on the discrimination probabilities of two algorithms

由图7分析可知，不同的航迹起始时间两种算法真实目标鉴别概率均保持稳定，而假目标鉴别概率均随着航迹起始时间的增加而增大。同样可以看出弹载雷达位置误差存在的情况下，本文算法真实目标鉴别概率高于文献[28]算法。

3.5 航迹关联阶段仿真验证

设置两个距离欺骗式假目标，欺骗距离分别为-1 000 m、-2 000 m，两部雷达导引头位置误差为100 m，其他设置同3.1节。航迹关联时间为7 s。为验证航迹关联鉴别假目标的能力，在航迹起始阶段不剔除假目标，主动雷达导引头跟踪产生3条航迹，被动雷达导引头跟踪得到1条航迹。主动雷达导引头3条航迹与被动雷达导引头航迹两两进行航迹关联的马氏距离在各个时刻的值如图8所示，航迹关联卡方检验统计量及均值如表2所示。

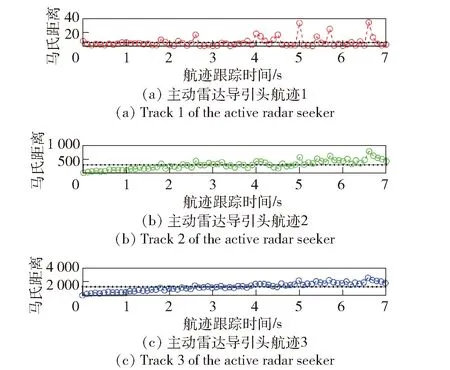
图8 主动与被动雷达航迹关联不同时刻的马氏距离Fig.8 Mahalanobis distance of active/passive radar track correlation at different times

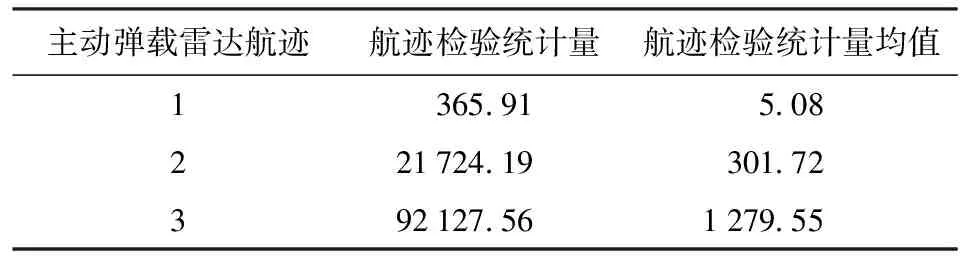
表2 航迹关联检验统计量及其均值

卡方检验显著性水平为0.005，状态矢量长度为6，观测时间间隔为0.1 s，关联的状态矢量个数为70，通过查表可得到自由度为420的卡方检验门限值。由图8和表2可以分析得出，只有主动雷达导引头航迹1与被动雷达导引头航迹的关联检验统计量低于门限值，这两条航迹关联成功，判别主动雷达导引头航迹1对应于真实目标。其余两条主动雷达导引头航迹的检验统计量远远大于门限，将其判别为假目标。该仿真实验验证了航迹关联进一步剔除假目标的可行性。

3.6 本文方法效果验证

通过3.1节～3.4节仿真结果可以看出，在存在雷达位置误差的实际情况下，在航迹起始阶段本文算法同文献[28]中未考虑雷达位置误差的算法相比，本文算法可以保证较高的真实目标鉴别概率，而假目标鉴别概率会略低于文献[28]算法，本文进一步通过序贯航迹关联鉴别剩余假目标。为验证航迹关联再次剔除假目标效果，设置雷达导引头位置误差为100 m，其余设置同3.1节，将本文算法在航迹起始阶段、航迹关联阶段的假目标鉴别效果同文献[28]航迹关联阶段的假目标鉴别效果进行对比，结果如图9所示。

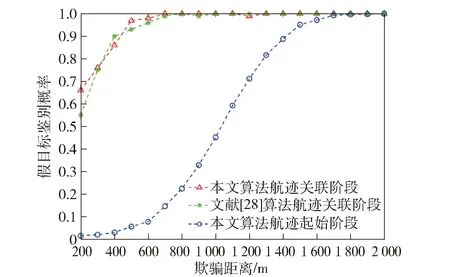
图9 假目标鉴别效果对比Fig.9 Comparison of false-target discrimination results

由图9可以看出：

1)当存在100 m的弹载雷达位置误差情况下，将本文算法航迹起始阶段和航迹关联阶段假目标鉴别效果进行对比可以发现，本文算法在航迹起始阶段考虑雷达位置误差鉴别假目标的基础上增加序贯航迹关联可有效提高假目标鉴别概率。

2)结合航迹起始阶段仿真实验结果以及本文算法与文献[28]算法航迹关联阶段的假目标鉴别结果可以看出：本文算法能够在保证较高的真实目标鉴别概率条件下，通过后续的序贯航迹关联后最终的假目标鉴别效果可达到文献[28]的假目标鉴别水平，弥补了本文算法航迹起始阶段由于考虑雷达位置误差导致假目标鉴别概率略低于文献[28]的不足。

4 结论

本文针对敌方干扰手段不断提高、单部弹载雷达抗距离式欺骗干扰效果差的问题，提出主被动异构弹载雷达组网协同抑制假目标的方法。在航迹起始阶段考虑组网内弹载雷达导引头位置误差，利用角度信息进行真假目标鉴别，剔除部分假目标；在航迹关联阶段通过序贯航迹关联算法进一步剔除剩余假目标。通过仿真证明，本文所提考虑弹载雷达位置误差的主被动异构弹载雷达组网抑制假目标干扰方法可以在保证较高的真实目标鉴别概率条件下对距离欺骗式假目标进行有效抑制。