基于钻柱横向振动模型的动力学分析

杨 琼，褚衍东，徐 璐

（1.兰州交通大学 机电工程学院，兰州 730070；2.兰州交通大学 数理学院，兰州 730070）

石油勘探是关系国民生计的重大工程.由于井眼的限制，勘探人员对钻柱进入地下复杂的运动状态并不是十分了解.因此，借助科学手段来研究钻柱进入地下的运动状态是十分必要的.在钻进过程中，当钻头运动时，它与土地接触时将造成钻具和钻头的过早磨损并产生主要的振动.而钻柱的振动情况可以清晰地反映设备的运动状态及地底情况［1］.基于这一原因，国内外学者开始了对底部钻柱动力学特性的研究.借助ANSYS等软件探讨了钻铤长度、钻井液密度、钻柱长度和壁厚、钻压以及防磨套间距等参数对钻柱横向振动的影响.例如，韩春杰［2］研究了水平井钻柱的横向振动问题.Tian［3］等分析了不同工况下钻柱横向振动中固有频率的变化趋势.Marcin［1］等研究了一类新型实验钻机底部钻具组合（BHA）的前后旋及共存问题.田家林［4］等基于动力学理论及数值求解方法，研究了整个井下钻柱的纵向和横向耦合振动问题.Zhang［5］等将加权残差法与有限元法结合来研究预弯曲摆式钻具组合的横向振动.在考虑钻头的摩擦及钻头的切削作用下，贾晓丽［6］等从数值上分析了无量纲化控制参数对钻柱粘滑振动特性的影响.Wang［7］等基于动力学知识设计了一种用于控制空气钻井中井斜的超前摆底部钻具组合.Zhang［8］等以一类旋转钻井的轴向和扭转耦合系统为研究对象，分析了不同失稳状态下系统的收敛性和鲁棒性.

随着混沌理论的兴起使得人们认识到，复杂的钻柱行为实际上可以用低维模型来描述，对这种模型的详细研究除了可以提高我们对钻柱动力学的理解之外，还可能为防止不必要的钻柱磨损现象提供一些线索，从而更好地控制钻柱的运动行为.据我们所知，钻井过程中由钻铤偏心引起的旋转会导致剧烈的横向振动，这一过程可以归结为不平衡转子的旋转运动.随着转子动力学［9-10］的发展，研究者们开始从转子动力学的角度来分析旋转钻铤的运动特性.Jansen首次将转子动力学理论应用于钻柱系统，所得结果较好地反映了钻柱的动力学特性［11］.Qiu［12］研究了粘滑运动中，参数变化对钻柱系统出现分岔和混沌的影响.王明杰［13］考虑了钻柱轴向-横向-扭转振动耦合系统的动力学特性.朱安茂［14］以钻柱内部钻井液和环空内钻井液的水平钻柱横向振动模型为研究对象，讨论了内外钻井液流速、钻井液密度等因素对钻柱横向振动特性的影响.Wiercigroch［15］等讨论了含有时滞和粘性阻尼的两自由度钻柱振动耦合模型的动力学特性.王宝金［16］等建立了水平井钻柱涡动的动力学方程，分析了钻柱自重、井壁摩阻、钻井液流速等因素对水平井钻柱涡动规律的影响.Wiercigroch［18］等研究了井下低维钻柱系统复杂的动力学特性.Irawan［19］等借助有限元方法研究了钻柱的横向振动问题.虽然上述文献详细的列举了不同工况下，系统参数对钻柱系统复杂动力学特性的影响，但借助数值延拓和分岔技术对钻柱系统稳定性的研究依然鲜见.本文以钻柱的横向振动模型为研究对象，借助Lyapunov直接法，推导出使得系统保持稳定的参数条件.通过数值实验，分析了系统出现涡动现象及横向振动的参数范围.找到了符合实际的最优参数.为减弱钻具磨损，提高钻柱的工作效率提供了一定的参考.

1 力学模型

地下钻井组合通常由钻铤、稳定器和钻头组成.图1为偏转钻铤在（X1，X2）平面上的截面图，其中X1，X2为钻铤相对于井孔中心的几何正交位移，m；s0为稳定器间隙，m；φ为稳定器摩擦角，rad；M为钻铤的质量，kg；kf为等效流体阻尼系数，kg/m；Ω是转速，m/s；e0是钻铤的质量偏心率；k为钻铤截面的等效抗弯刚度，kg/m2；p表示钻铤几何中心与稳定器中心之间的距离，m.

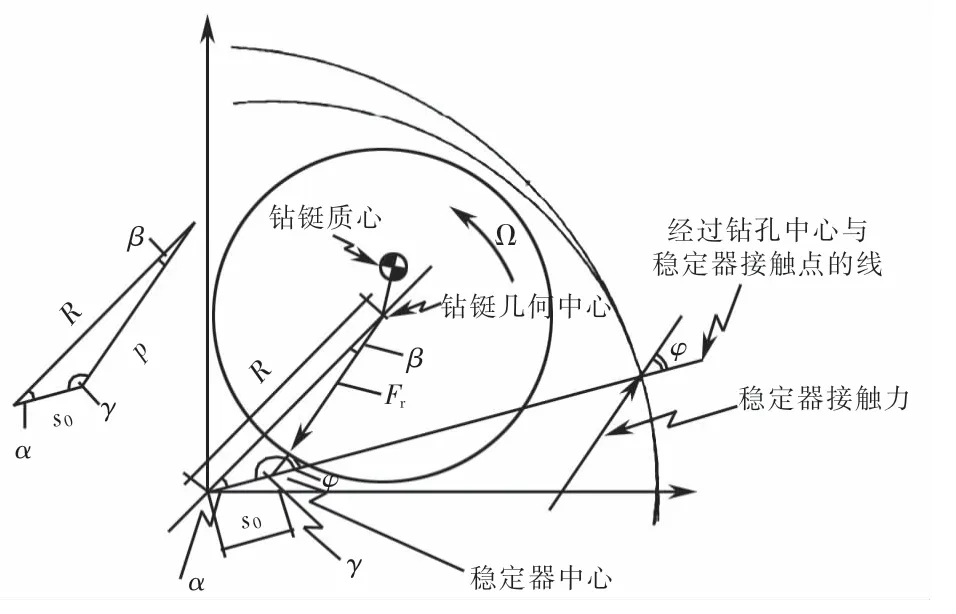
图1 偏转钻铤在平面上的截面图Fig.1 The cross section of a deflected drill collar in theplane

为了准确描述带有恒定角速度钻柱系统的运动，Jansen作出假设（弹性钻铤处于第一弯曲模态；井孔是完全垂直的；稳定器是无质量的），并建立以下模型方程［11］：

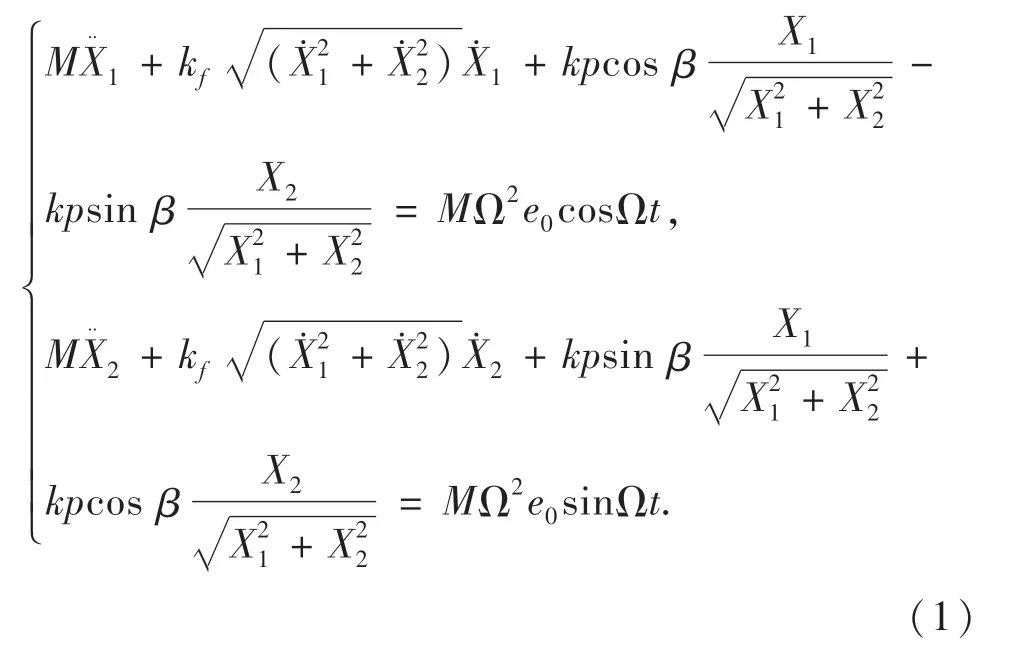
依据图1的几何结构，可以得到：

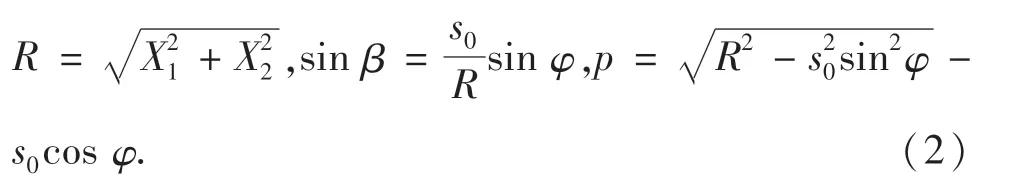
借助（2）式及一阶Taylor展开，方程（1）可写为：

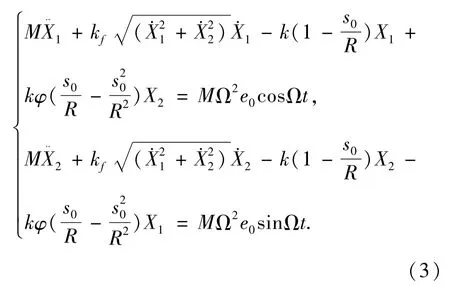
引入无量纲变量：

其中钻铤间隙c0=（Dh-Dc）/2（Dh和Dc分别为孔的直径和钻铤的直径），m；钻铤固有频率Hz；α为接触参数.得到如下系统：

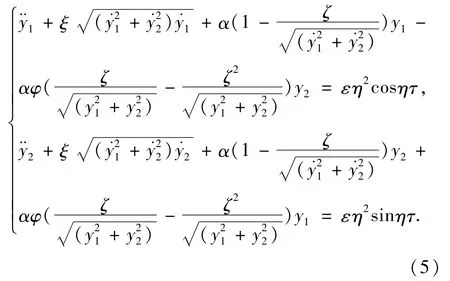
为了便于研究钻柱系统的动力学特性，对系统（5）作坐标变换［17］，并设阻尼系数φ=0，摩擦系数ξ=0，得到如下自治系统：

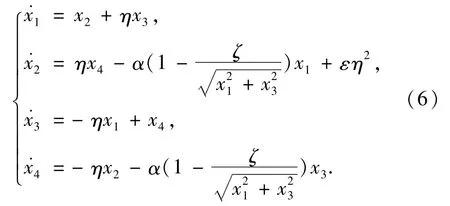
2 稳定性分析

系统（6）描述了钻柱的横向振动，其平衡点对应于系统（5）的同步涡动情况.令系统（6）的平衡点为pe=（x0，y0，z0，w0），其中

且|x0|＞ζ，对平衡点pe作一个小扰动，即

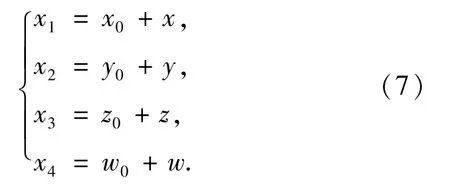
将（7）式代入（6）式可得：

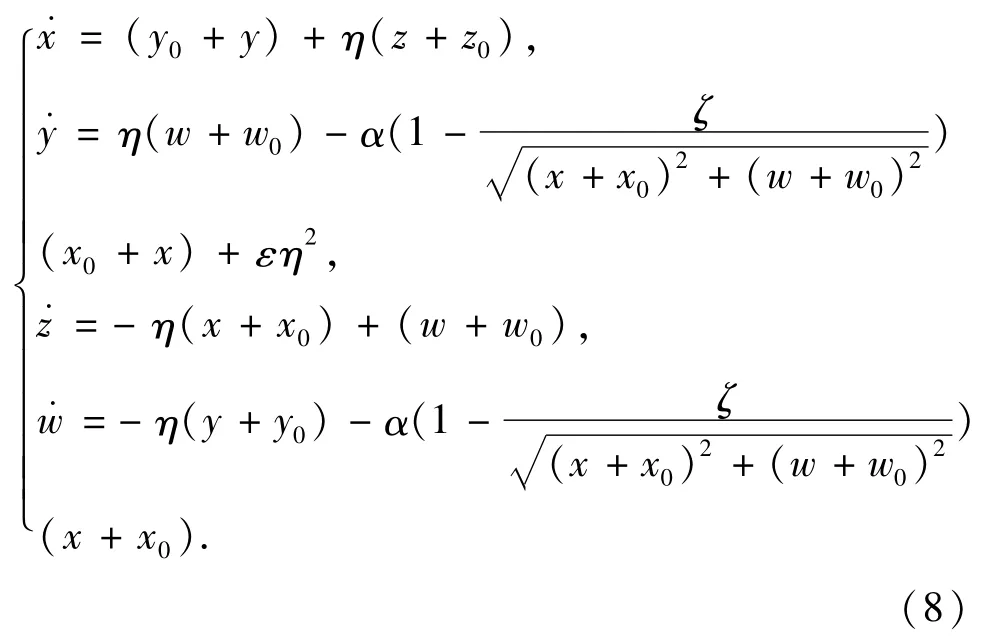
将（8）式在（0，0，0，0）处作Taylor级数展开得：

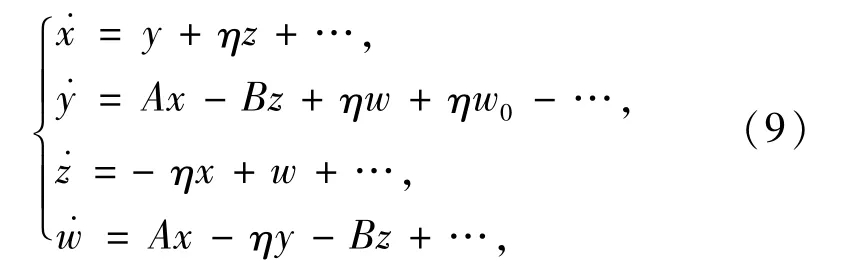
其中，

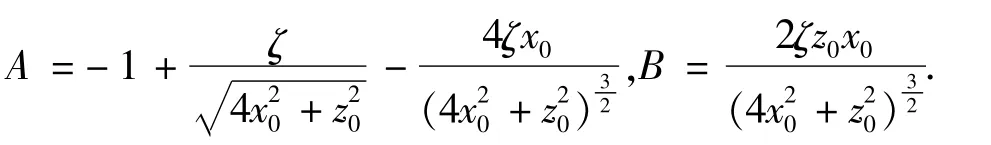
系统（6）可写为：

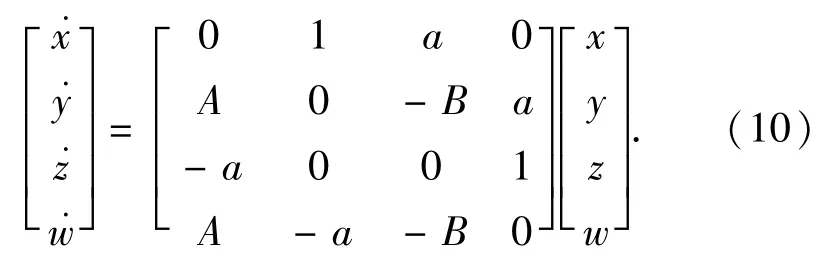
构造如下Lyapunov函数：

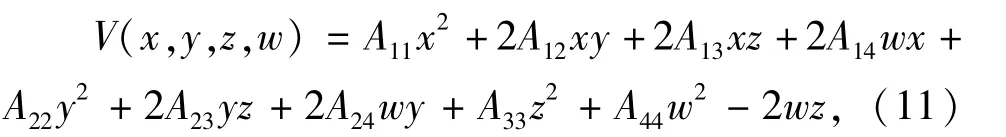
其中，

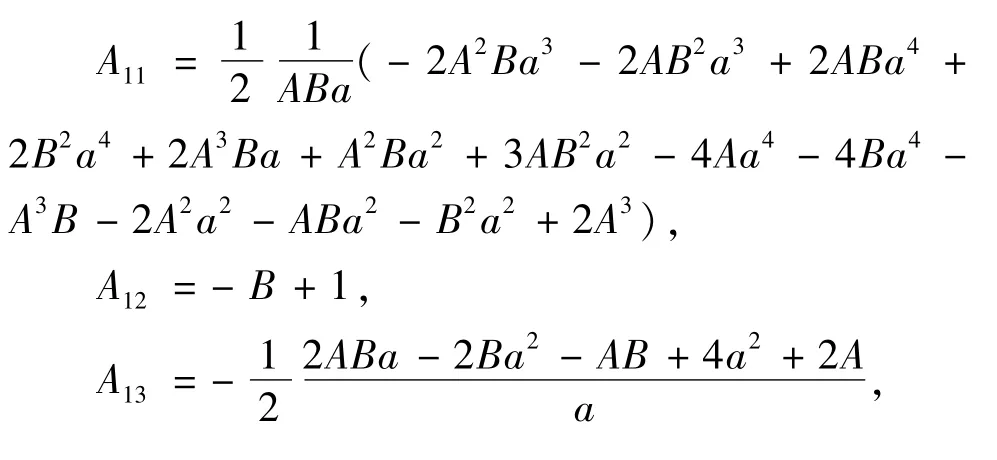
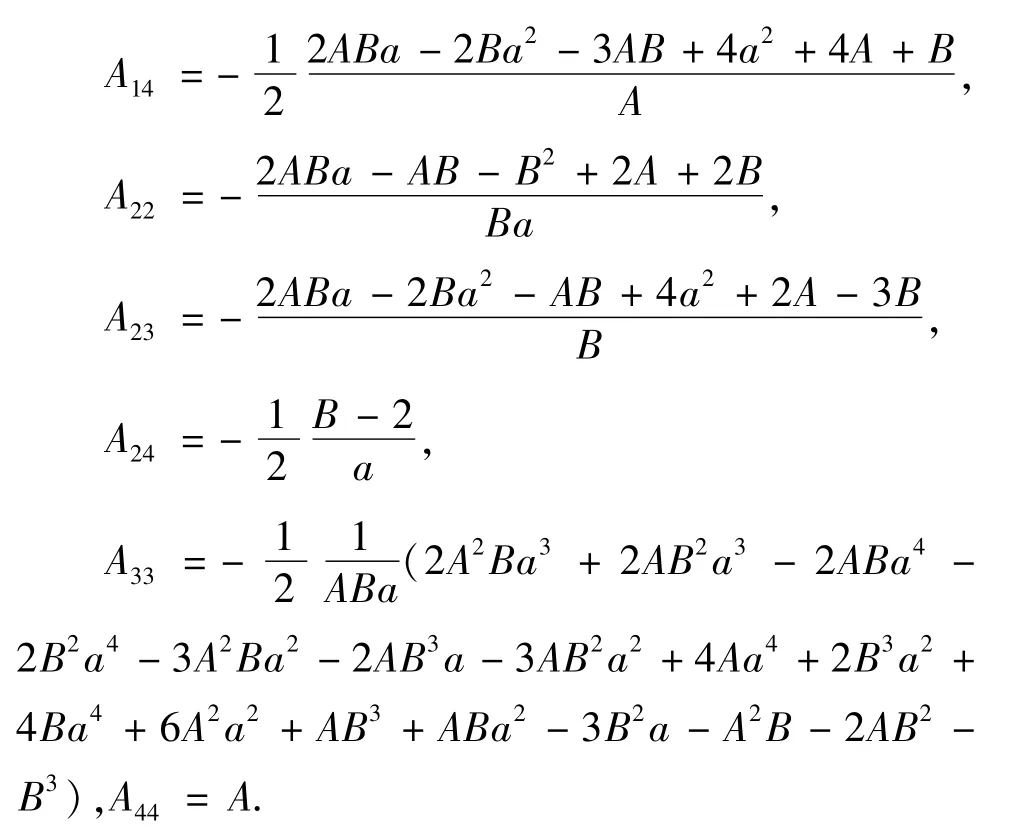
将Lyapunov函数写为如下矩阵形式：

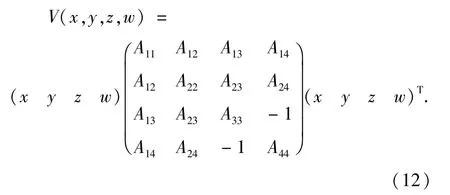
令Pi（i=1，2，3，4）为V（x，y，z，w）所确定特征矩阵的主子式，即

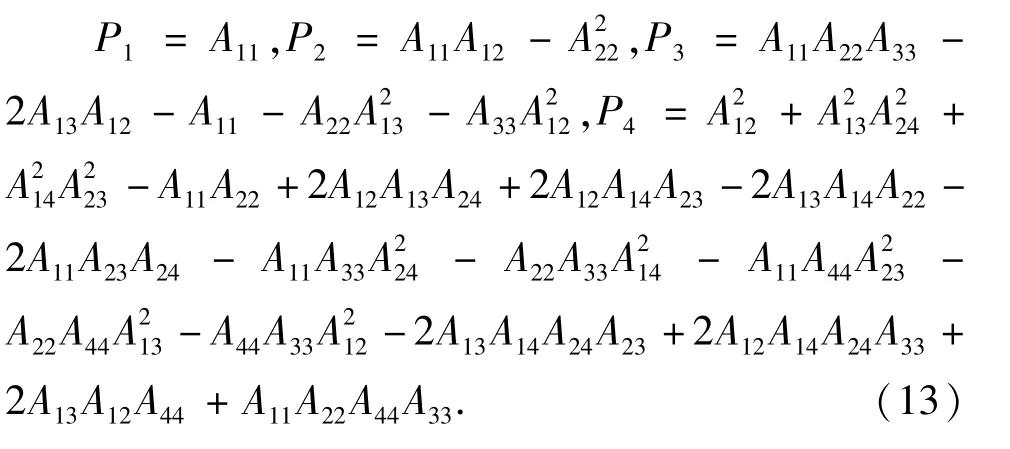
依据Sylvester引理［20］可知，当时，V（x，y，z，w）=-B（x，y，x，w）+…是正定的，对Lyapunov函数求导可得：

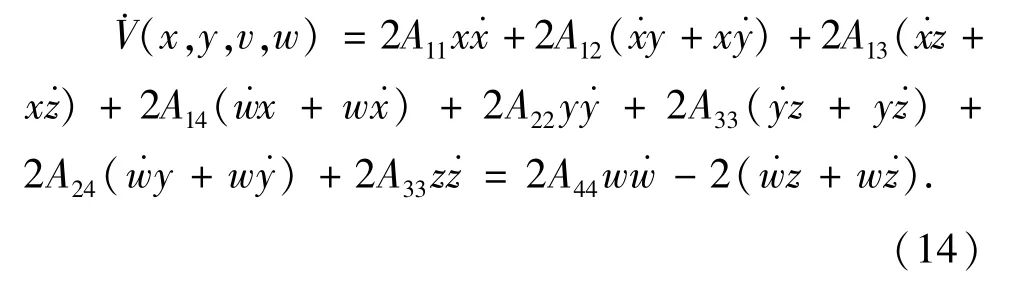
将（9）式代入（14）式得到：

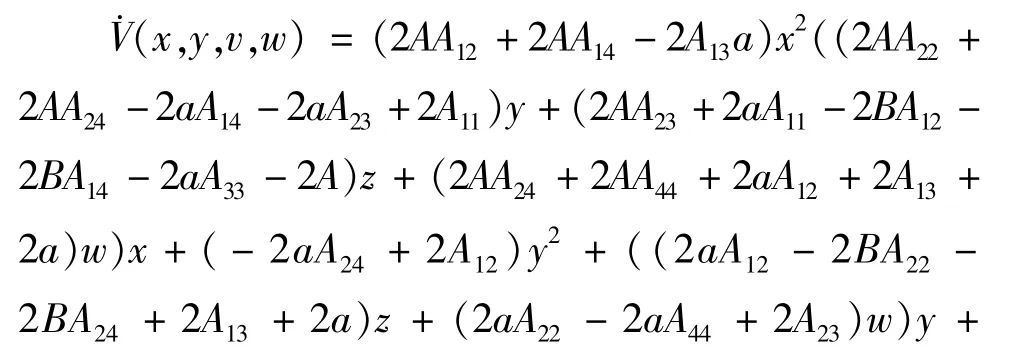
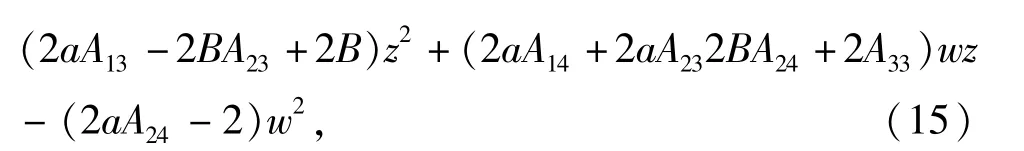
3 数值模拟

3.1 外激励频率变化对系统同步涡动的影响

涡动是钻柱系统横向振动诱导的最剧烈的运动形式，而同步涡动的出现会降低钻井效率，加速钻铤的磨损，这对钻柱系统来说是十分不利的.因此，我们可以借助不同参数条件下的稳态解曲线（图2），得到系统出现同步涡动的参数范围，避免系统出现同步涡动现象，提高钻柱井下勘探的效率.图2中实线表示具有物理意义的稳态解，虚线表示具有非物理意义的稳态解.观察图2（a）可知，当稳定器间隙ζ小于钻铤的偏心率ε时，随着外激励频率η增大，系统（6）的平衡点数目（最多不超过2个，包含了物理解和非物理解）发生显著的变化.当η＜1时，系统（6）中符合物理意义的平衡点只出现1个，即在钻柱运动过程中会出现1次同步涡动现象.当η→1时，没有平衡点，即没有同步涡动出现.当η＞1时，系统的平衡点的数目又增加为2个，但只有1个具有物理意义的，即系统的同步涡动又恢复为1次.也就是说，在ζ＜ε的情况下，随着外激励频率的增大，系统的同步涡动最多出现1次.观察图2（b）可知，在稳定器间隙ζ大于钻铤的偏心率ε情况下，当η＜1时，系统的同步涡动次数会逐渐增加.当η→1时，同步涡动次数增加到2次.当η＞1时，系统会出现不符合物理意义的2个平衡点，即系统不会出现同步涡动.

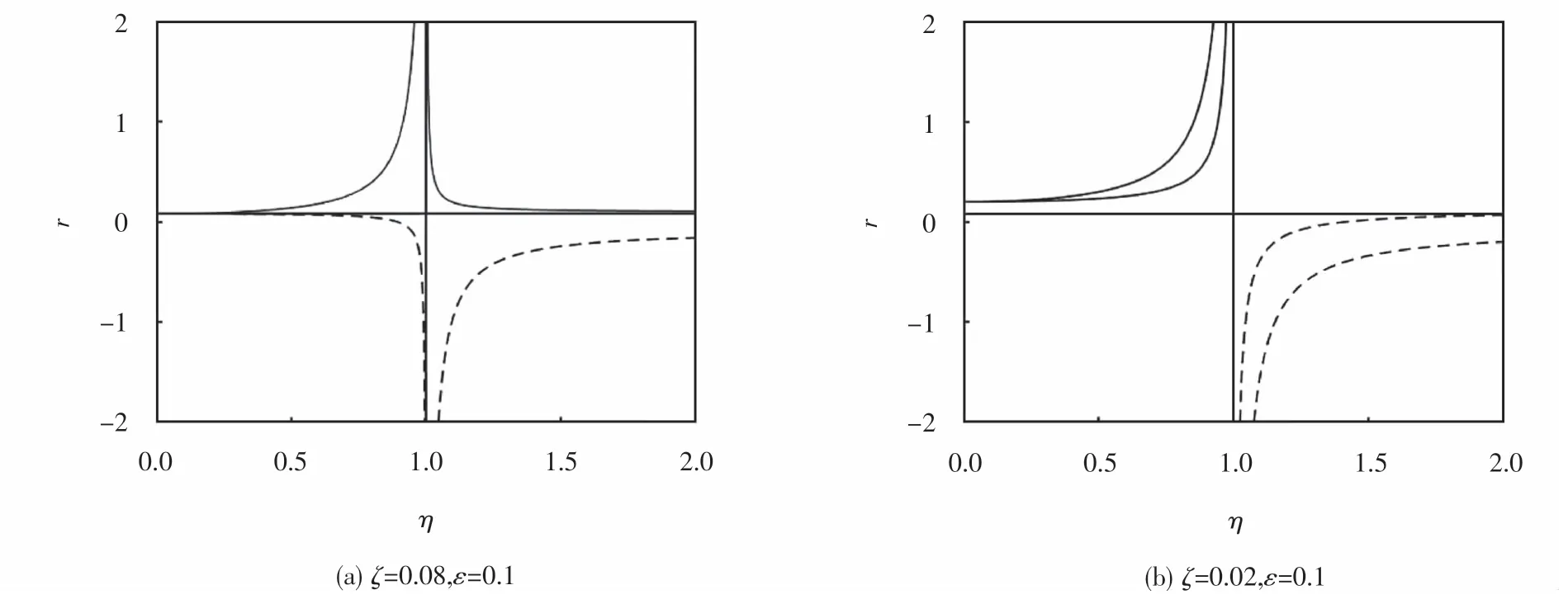
图2 稳态解曲线Fig.2 Stationary solution curve

3.2 外激励频率及质量偏心率变化对系统动力学特性的影响

下面研究稳定器间隙ζ大于钻铤偏心率时，外激励频率η变化对系统动力学特性的影响.固定参数α=1.0，ζ=0.2，ε=0.1，借助变步长的四阶龙格库塔法，可得不同外激励频率对应的相图、时间响应图、Poincaré截面图.观察图3～图5可知，当0＜η＜1时，系统（6）的运动始终处于周期运动状态，对应系统（5）会出现准周期运动.因此，在钻进过程中，为了减弱稳定器的磨损，提高钻柱系统的工作效率，外激励频率η取值尽量不超过1.

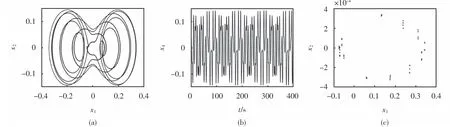
图3 η＝0.001对应的相图、时间响应图、Poincaré截面Fig.3 Corresponding phase diagram，time response diagram，Poincarésection ofη＝0.001

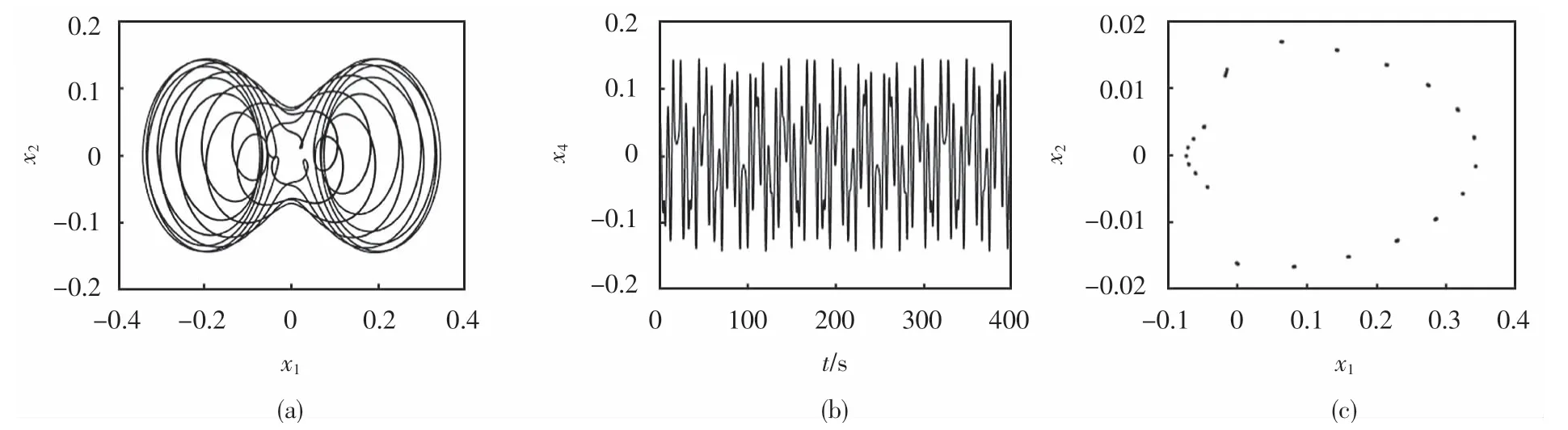
图5 η＝0.05对应的相图、时间响应图、Poincaré截面Fig.5 Corresponding phase diagram，time response diagram，Poincarésection ofη＝0.05

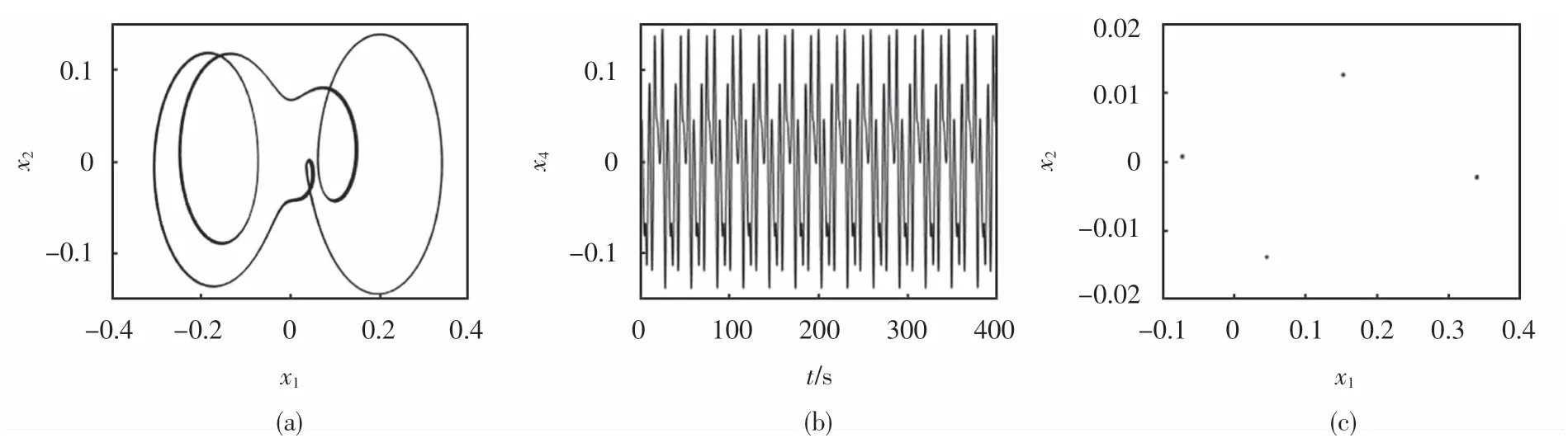
图4 η＝0.040 8对应的相图、时间响应图、Poincaré截面Fig.4 Corresponding phase diagram，time response diagram，Poincarésection ofη＝0.040 8

图6～图7研究了在稳定器间隙ζ大于钻铤偏心率ε的情况下，当外激励频率η超过1时，钻铤偏心率变化对系统动力学特性的影响.图6为偏心率ε取不同值对应的分岔图.观察图6（a）可知，当参数η在［1，2］内逐渐增大时，系统（6）进入混沌运动状态.当参数η超过某一临界频率时，系统不再出现混沌运动，即外激励频率越低越容易出现混沌运动.对比图6（a）与图6（b）可知，当参数ε增大时，低频区域出现混沌的宽度减小，而当外激励频率超过临界值时，系统会出现周期运动.图7为外激励频率η=1.01时，对应的相图及时间响应图.观察图7可知，当外激励频率η=1.01时，系统出现混沌运动.因此，为了避免钻柱系统出现混沌运动，我们可以适当的增大外激励频率，减弱钻铤的磨损.

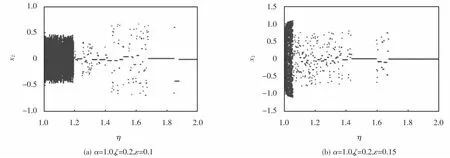
图6 ε取不同值对应的分岔图Fig.6 The bifurcation diagram corresponding to differentεvalues

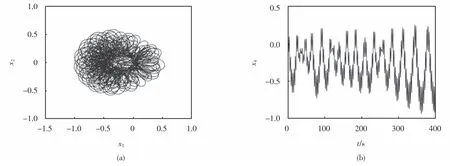
图7 η＝1.01对应的相图、时间响应图Fig.7 Corresponding phase diagram，time response diagram ofη＝1.01

4 结论

本文研究了参数变化对含简谐外激励钻柱横向振动模型的影响，主要结果如下：

1）外激励频率、质量偏心率、稳定器间隙，对系统同步涡动现象的出现和次数有很大的影响.当稳定器间隙小于钻铤的偏心率时，只要外激励频率不等于1，系统总会出现同步涡动现象；当稳定器间隙大于钻铤的偏心率时，只有在外激励频率小于1的情况下，系统才会出现同步涡动现象.

2）在稳定器间隙大于钻铤的偏心率的情况下，当外激励频率小于1时，钻柱系统始终处于周期运动状态.当外激励频率大于1时，系统出现混沌运动，且当钻铤偏心率增大时，钻柱系统在低频区混沌运动区域的面积减小.