基于多层复杂网络的中欧班列运输网络关键节点识别研究

冯芬玲，蔡明旭，贾俊杰

(中南大学，交通运输工程学院，长沙 410075)

0 引言

中欧班列是由中国铁路总公司组织，按照固定车次、线路及班期等条件开行，往来于中国与欧洲及一带一路沿线各国的集装箱国际铁路联运班列。2011年3月，第1列中欧班列从重庆出发，直达德国杜伊斯堡，打通了中欧国际贸易的陆路大通道。在政策推动以及外贸需求增加等有关因素的作用下，中欧班列运输规模不断扩大，运输网络覆盖亚欧大陆多个国家地区，截至2022 年7 月，中欧班列已打通73 条运行线路，通达欧洲24 个国家的190 多个城市[1]，呈现欣欣向荣的发展态势。但与此同时，突发公共卫生事件、地缘政治冲突及地理环境灾害等因素为中欧班列的运输稳定性和时效性带来了巨大挑战。例如，新冠疫情以来，中欧班列货运量激增，部分运输节点出现拥堵，例如，马拉舍维奇最严重时火车过境换装时间高达10 d，严重制约运输时效[2]。同时，俄乌冲突战火蔓延至乌克兰首都基辅火车站，使中欧班列途径乌克兰线路被迫中断，对整体运输网络带来一定冲击。关键运输节点的故障或中断，会影响整体运输网络的货物流动。因此，运用复杂网络方法构建中欧班列运输网络，识别网络中的关键节点，并采取针对性保护措施，对保障中欧班列平稳运行具有重要作用。

中欧班列运输网络本质上属于交通网络，大量学者利用复杂网络理论研究不同运输方式交通网络的节点重要性评价问题。张兰霞等[3]基于中国高速铁路网的结构特征构建中国高速铁路地理网、车流网以及服务网这3个网络模型，并在不同情况下模拟攻击地理网，找出了地理网中较为重要的节点，为本文构建中欧班列运输网络提供了参考。WANG 等[4]结合航空货运网络的拓扑结构、行业特点和方向性，提出一种基于TOPSIS 法的节点重要性评估方法。JIANG 等[5]基于2017年6月～12月的航线数据构建“海上丝绸之路”集装箱航运网络，并分析其拓扑特征。汤霞等[6]构建中国出口集装箱运价指数波动复杂网络模型，探究集装箱运价波动呈现群簇性、周期性、持续性和渐进性的动态特征。胡立伟等[7]考虑城市交通拥塞情况，构建城市路网交通拥塞因子风险复杂网络模型，并进行了节点重要性评估。针对中欧班列方面，部分学者同样利用复杂网络理论开展节点重要性研究。ZHANG 等[8]基于Space-P 方法构建中欧班列运输网络，证明了其小世界和无标度特性，并运用结构洞理论计算中欧班列运输网络节点的重要性，但其未考虑中欧班列服务网络的特性。之后，吕敏等[9]从运输风险角度出发，综合考虑节点网络拓扑特征和运输服务属性，利用熵-TOPSIS 排序中欧班列运输网络节点，并构建聚类节点风险识别模型划分运输风险节点，但其网络构建时未考虑节点的实际空间距离。

综上所述，目前针对交通网络节点重要性的研究较为丰富，但是针对中欧班列方面均是从运输关系方面构建运输网络后开展关键节点识别研究的基础，缺乏考虑运输实际过程等因素。其次，大多节点重要性评估研究多定性分析评估结果的好坏，缺乏对方法的有效性验证，亟需更为科学的评估方法。因此，本文在之前学者研究的基础上，选取国外主要开行城市、通道口岸以及《中欧班列建设发展规划2016—2020》规定的主要货源地、铁路枢纽、沿海重要港口及沿边陆路口岸为节点，按照各班列运营平台公司的开行线路图，首先，构建同时考虑中欧班列运输网络节点实际空间结构与运输关系的多层复杂网络；其次，针对多层网络提出改进TOPSIS法及灰色关联分析的评估方法识别网络关键节点；之后，利用动力学传播模型检验识别结果的有效性，验证方法的优越性；此外，根据识别结果提出针对性的节点保障建议。研究从网络结构方面丰富了中欧班列运输组织优化的研究体系，可以为优化运输网络，提高网络鲁棒性提供科学依据。

1 中欧班列运输网络构建

中欧班列运输网络由轨道和车站等硬件基础设施以及通行于轨道之上承载货物的列车构成，因此，具有一定的层次性，包含了两层网络性质。下层是以开行中欧班列的城市为节点，以连接两个城市之间的实际线路为边组成的基础路网，是中欧班列进行货物运输的基础；上层是以开行中欧班列的城市为节点，以列车开行线路经过的节点彼此连接为边形成的网络，由于对中欧班列相关网络的研究较少，因此，本文借鉴文献[3]对高速铁路网络的研究，将此网络称为中欧班列车流网络。中欧班列运输网络如图1所示。

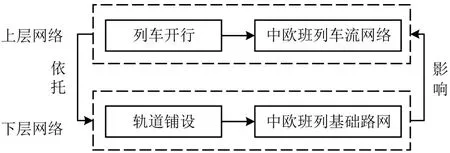
图1 中欧班列运输网络示意Fig.1 Schematic diagram of CR express transportation network

根据中欧班列运输网络特征，定义中欧班列多层复杂网络S=(Ggeo,Gtra)，其中，Ggeo(Vgeo,Egeo,ωgeo)代表基础路网，基于Space-L方法构建，反映中欧班列运输网络的实际空间结构。Gtra(Vtra,Etra,ωtra)代表车流网络，基于Space-P方法构建，反映中欧班列运输网 络 中 各 城 市 间 的 关 联 关 系 。Vgeo=Vtra=(a1,a2,…,an-1,an)，其中，an为开行中欧班列的城市n。

在基础路网Ggeo中，Egeo为连接各节点城市之间的实际线路，考虑实际线路存在的物理属性差异及各节点城市的功能属性差异；ωgeo为相邻节点城市之间的通达时间，即

式中：Dij为城市i与城市j之间的线路长度；vij为列车在该线路上的运行速度；tij为列车在边境城市相连线路换装所需时间(h)。

在车流网络Gtra中，Etra为各节点城市间的连接关系；ωtra为各节点城市间是否存在联系，即

在中欧班列运输网络中，基础路网与车流网络具有相同性质的节点，同时，两层网络的连边性质不同，各个网络层相互独立，互不影响，因此，中欧班列运输网络符合多维型多层网络的概念。

2 中欧班列运输网络节点重要性综合评价方法

中欧班列运输网络属于多维型多层网络，目前，针对多层网络节点重要性评价的研究相对较少，考虑到本文建立的中欧班列运输网络中各网络层的连边性质差异较大，以及各网络层的结构特征并不相同，使用单一的重要性指标无法全面反映节点重要性，本文提出一种基于改进TOPSIS 法及灰色关联分析的多层网络节点重要性评价方法，评价中欧班列运输网络节点的重要性，步骤如下：

Step 1 将中欧班列运输网络按照组成关系拆解为中欧班列基础路网及中欧班列车流网络，选取节点重要性评价指标，分别计算每层网络的指标值。

Step 2 使用改进TOPSIS法计算节点在每个单层网络中的重要度评价值。

Step 3 使用灰色关联分析融合所有单层网络中的节点重要度评价值，得到节点在中欧班列运输网络的综合重要度评价值。

评价方法流程如图2所示。

图2 中欧班列运输网络关键节点识别方法流程Fig.2 Process of identifying key nodes in CR express transportation network

2.1 中欧班列多层网络节点重要性评价指标选取

目前，已经有很多评价节点重要性的指标，例如节点度和介数等。不同的指标在不同结构的网络中使用程度并不相同，且单一的指标并不能全面反映整个网络的节点重要性[10]。因此，为度量中欧班列运输网络各个单层网络的节点重要性，本文从邻居节点、全局信息、特征向量以及结构洞等多个方面选取重要性评价指标。

(1)度中心性

度中心性反映节点周围邻居节点的稠密程度，度中心性越大，则该节点在网络中的影响力越大。计算公式为

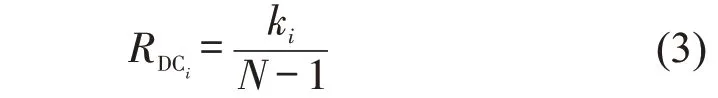
式中：ki为现有与节点i相连的边的数量；N为网络中的节点数。

(2)介数中心性

介数中心性反映了节点的中介能力，介数中心性越大，代表节点在网络中的地位越重要。计算公式为

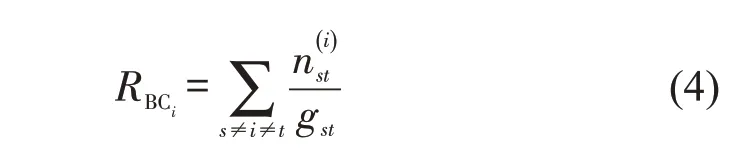
(3)接近中心性

介数中心性反映了节点的中介能力，介数中心性越大，代表节点在网络中的地位越重要。计算公式为

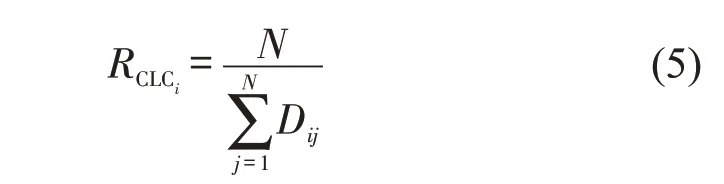
(4)特征向量中心性

特征向量中心性反映节点与其他节点的接近程度，接近中心性越大，代表节点的影响力越大。计算公式为

式中：c为比例常数；A为网络的邻接矩阵。

(5)网络约束系数

网络约束系数反映一个节点对网络中其他节点的依赖程度，其值越大，依赖程度越大，占据结构洞的可能越小。计算公式为

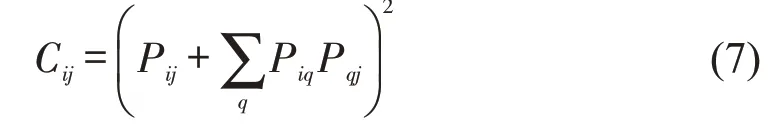
式中：节点q为节点i与节点j的共同邻接点；Pij为在节点i的所有邻接点中节点j所占的权重比例。

(6)局部聚类系数

局部聚类系数反映该节点的邻居节点聚集成团的可能性，局部聚类系数越小，占据结构洞的可能性越大。计算公式为

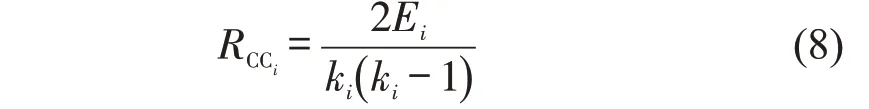
式中：Ei和ki(ki-1) 分别为节点i的ki个邻居节点之间实际存在的边数和可能存在的最大边数。

2.2 TOPSIS法及其改进

TOPSIS法由C.L.Hwang和K.Yoon于1981年提出，是一种经典的多属性决策方法。利用TOPSIS法可以将每个单层网络中的节点重要度评价问题转换为多属性决策问题，即将每个节点作为决策方案，将选取的每个节点重要性评价指标看作方案的评价指标，根据方案中各项评价指标值得到正理想解(最优方案)和负理想解(最劣方案)，通过计算各决策方案与最优方案的接近程度，对决策方案进行排序。传统的TOPSIS法并未考虑各项评价指标对方案的贡献程度，而在节点重要性评价过程中，不同评价指标对节点重要性的贡献往往是不同的。因此，本文提出一种基于极端随机树加权的改进TOPSIS 法，计算节点在中欧班列运输网络中每个单层网络中的重要度评价值。

2.2.1 初始决策矩阵构建及标准化

在中欧班列运输网络中，假设某个单层网络的节点数为N，节点重要性评价指标有M个，各节点在该网络中的指标值为xij(i=1,2,3,…,N;j=1,2,3,…,M)，得到初始决策矩阵U，即

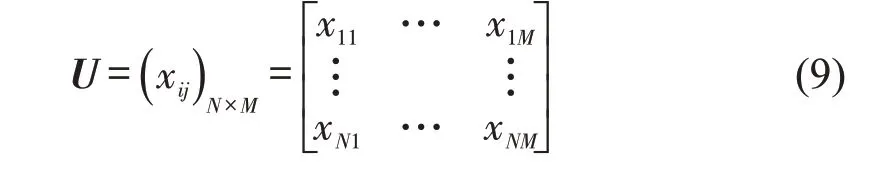
本文选取的重要性指标中，局部聚类系数与网络约束系数属于负向性指标，即指标值越小，反映节点重要性越高，其余指标均属于正向性指标。为了消除指标定义、量纲及数量级对评价造成的影响，需要将所选指标进行处理，得到标准化决策矩阵H。

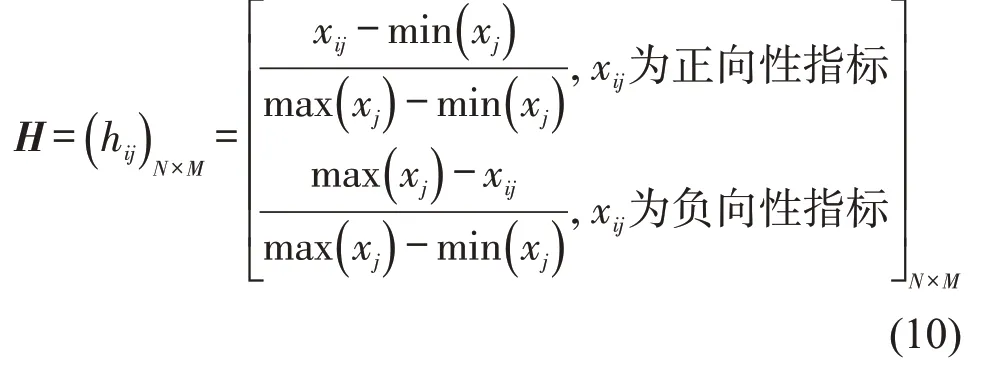
2.2.2 指标权重计算

在中欧班列运输网络中，每个单层网络的结构并不相同，因此，同一节点重要性指标对不同网络层中的节点重要度评价值的贡献程度也不完全相同。为了更加准确地计算节点在各网络层的重要度评价值，本文运用极端随机树算法计算指标权重。

极端随机树是一种机器学习算法，其生成的决策树能够通过学习拟合指标之间的相互作用，计算出每个指标在决策树中的贡献程度，以此衡量各个指标的相对权重[11]。本文以选取的重要性评价指标作为输入变量，以反映节点对单一网络层影响程度的补图效率变化率作为输出变量，其中，补图效率变化率指该网络层中删除该节点后的网络效率与原网络效率的差值。根据输入变量在所有决策树中节点熵的平均改变量得到重要性评价指标的权重。

2.2.3 单层网络节点重要度评价值计算

根据极端随机树算法得到每个指标的权重后，对标准化决策矩阵H进行加权，得到加权决策矩阵R，即

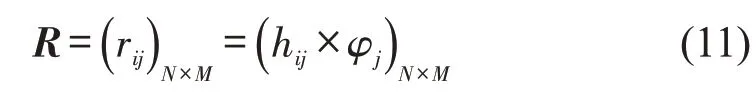
式中：φj为第j个指标的权重。

根据加权决策矩阵R中每个指标的最大值与最小值确定正理想解R+和负理想解R-，即

计算每个方案到正理想解和负理想解的距离，即

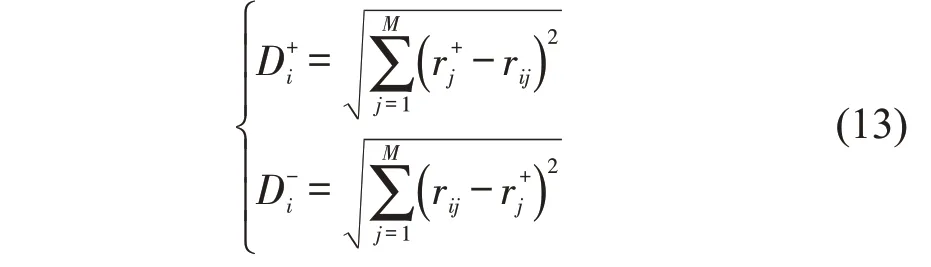
计算每个方案与正理想解的贴近度Zi，作为节点i在该网络层的重要度评价值，即

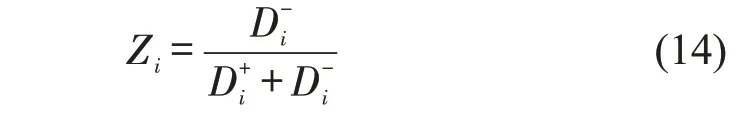
2.3 基于灰色关联分析的多层网络节点重要性融合算法

利用改进TOPSIS法计算出节点在中欧班列运输网络中每个单层网络中的重要度评价值后，需要综合评估节点在整个中欧班列运输网络的重要度，因此，本文提出一种基于灰色关联分析的多层网络节点重要性融合算法，其本质思想是：在中欧班列运输网络中，选取每个单层网络中最大的重要度评价值进行组合，作为参考对象，计算任意节点与参考对象的灰色关联度，关联度越大，则该节点在整个网络中的重要性越大。

2.3.1 样本矩阵构建及标准化

在中欧班列运输网络中，每层网络中的节点数量与性质相同，网络拓扑结构互不相同。假设中欧班列运输网络可以分解为P个单层网络，每个单层网络中包含Q个节点，利用上文提出的改进TOPSIS 法计算节点i在网络层j中的重要度评价值zij，构建样本矩阵Z，即

为了降低不同节点在同一网络层中的重要度评价值波动幅度，对矩阵Z按行进行归一化，得到标准矩阵Z′，即2.3.2 确定评价对象与参考对象

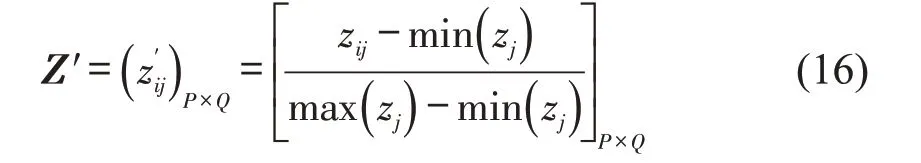
本文将节点在不同网络层中的重要度评价值作为评价对象，即矩阵Z′中的每一列元素都是评价对象，选取矩阵Z′中每一行的最大元素作为参考对象S，即

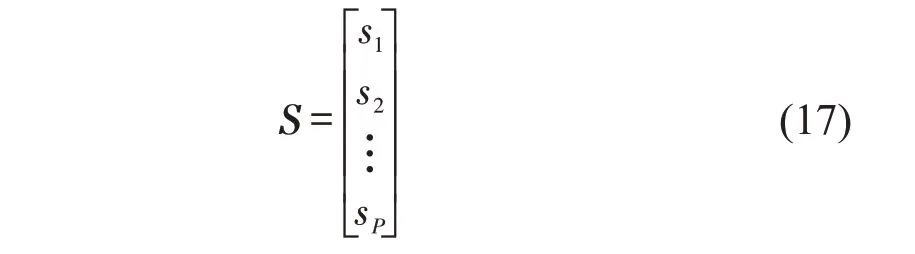
式中：sP=max(),j=1,2,…,Q。

2.3.3 多层网络节点综合重要度评价值计算

计算矩阵Z′中每个节点与参考对象S的灰色关联度Rj，作为节点在中欧班列运输网络中的综合重要度，即

式中：ξij为zij与参考对象的灰色关联系数；ρ为分辨系数，通常取0.5。

3 实例分析

本文选取截至2021 年5 月各班列公司的开行线路情况，以中欧班列途经及到达的国外主要城市以及《中欧班列建设发展规划2016—2020》规定的主要货源地、铁路枢纽、沿海重要港口及沿边陆路口岸为节点，构建中欧班列运输网络，评价网络中160个节点的重要性。

3.1 网络模型构建

根据式(1)和式(2)分别构建中欧班列基础路网和车流网络，组成中欧班列多层网络S，将各节点进行编号处理。利用谷歌地图寻找各个节点经纬度，下载Open Street Map中关于亚欧大陆的铁路数据，将其导入ArcGIS，根据节点经纬度量取各节点之间的实际地理长度，根据中欧班列的平均开行速度以及在口岸站的平均通过时间[12]，得到基础路网连边权值。中欧班列网络示意如图3和图4所示。

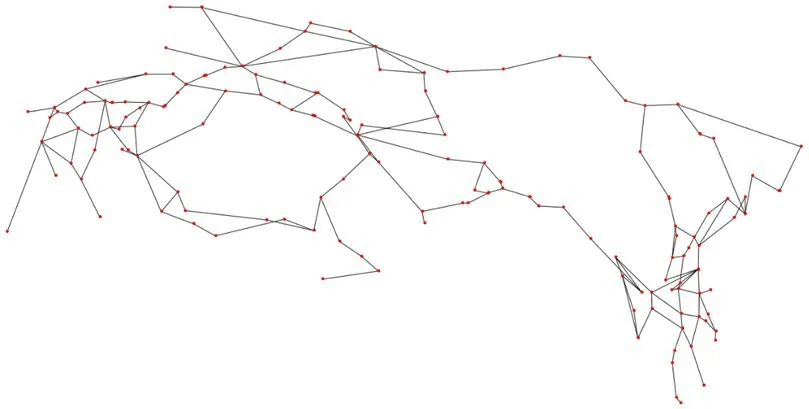
图3 中欧班列基础路网拓扑示意(隐去节点编号)Fig.3 Topological diagram of CR express basic road network(node number is hidden)

图4 中欧班列车流网络拓扑示意(隐去节点编号)Fig.4 Topological diagram of CR express train flow network(node number is hidden)

3.2 单层网络节点重要度评价

根据构建好的基础网络及车流网络，按照式(3)～式(8)，利用Python编程计算每个节点在基础路网及车流网络中的度中心性、介数中心性、接近中心性、特征中心性、网络约束系数以及局部聚类系数，得到节点重要性评价指标数据。

其次，根据各个节点在基础路网和车流网络中的指标计算值，分别构建决策矩阵，并对矩阵中的指标进行规范化处理，得到规范化决策矩阵Hgeo和Htra。

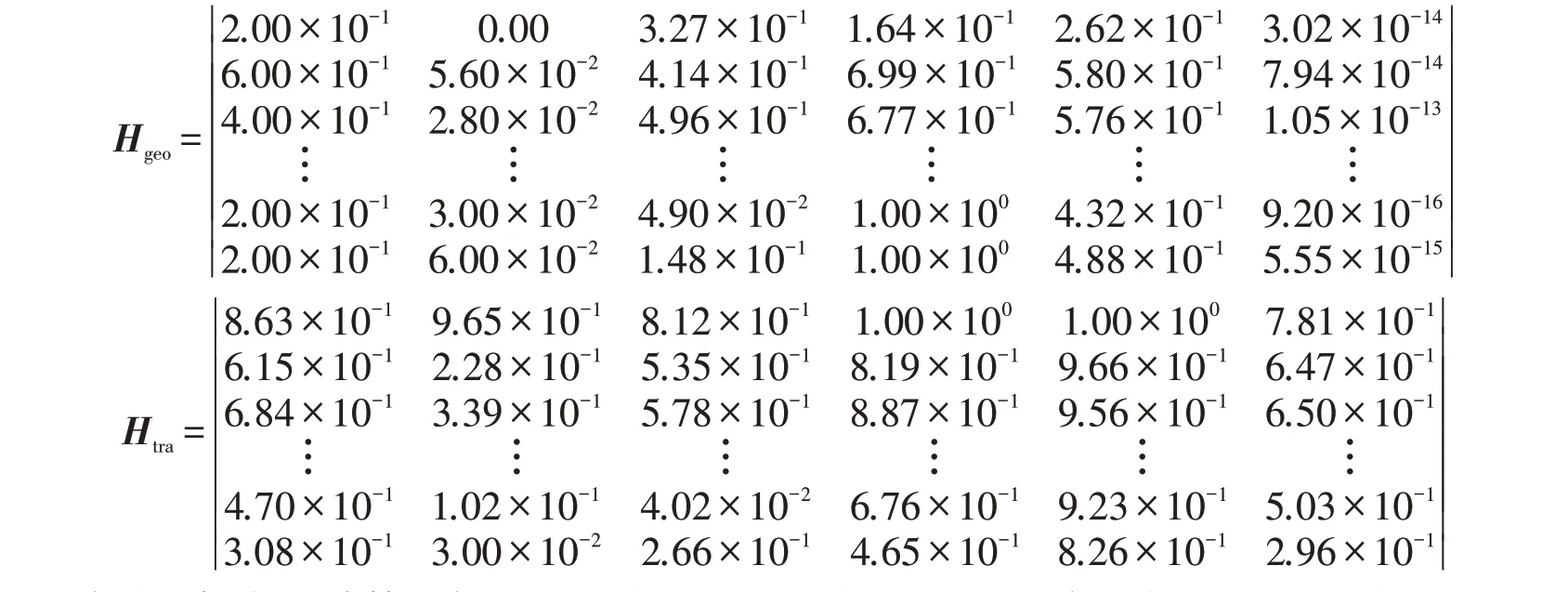
使用极端随机树方法计算指标权重。在基础路网中，当训练样本的比例为75%，决策树数量和最小分割节点数分别为10 和10 时，训练效果较好。指标排序及权重分别为：(1)介数中心性，权重为0.3676；(2)接近中心性，权重为0.2815；(3)度中心性，权重为0.2135；(4)网络约束系数，权重为0.0910；(5)特征向量中心性，权重为0.0383；(6)局部聚类系数，权重为0.0082。在车流网络中，当训练样本的比例为0.75，决策树数量和最小分割节点数分别为200 和4 时，训练效果较好。指标排序及权重分别为：(1)度中心性，权重为0.3872；(2)接近中心性，权重为0.3021；(3)特征向量中心性，权重为0.1518；(4)介数中心性，权重为0.0977；(5)网络约束系数，权重为0.0489；(6)局部聚类系数，权重为0.0124。

将指标权重分别代入相应的决策矩阵中，计算各节点在基础路网和车流网络中的重要度评价值，结果如表1所示。

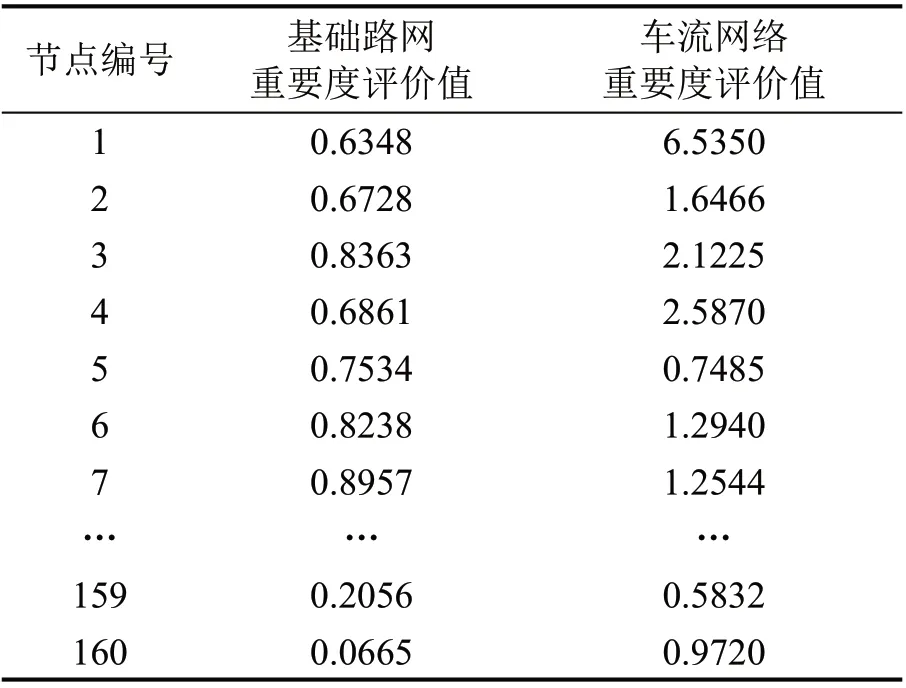
表1 单层网络各节点重要度评价值(部分)Table 1 Importance evaluation value of each node in a single-layer network(part)

3.3 节点综合重要度评价值计算

根据各个节点在基础路网和车流网络中的重要度评价值，构建样本矩阵，得到矩阵Z。

之后，根据式(16)和式(17)进行矩阵标准化和确定参考对象；最终，根据式(18)和式(19)计算中欧班列运输网络中各节点的综合重要度评价值，并作为节点重要性排名。研究表明，如果一个网络中5%～10%的关键节点失效，网络就会陷入瘫痪[13-14]。因此，本文列出综合重要度排名前10%的节点，结果如表2所示。

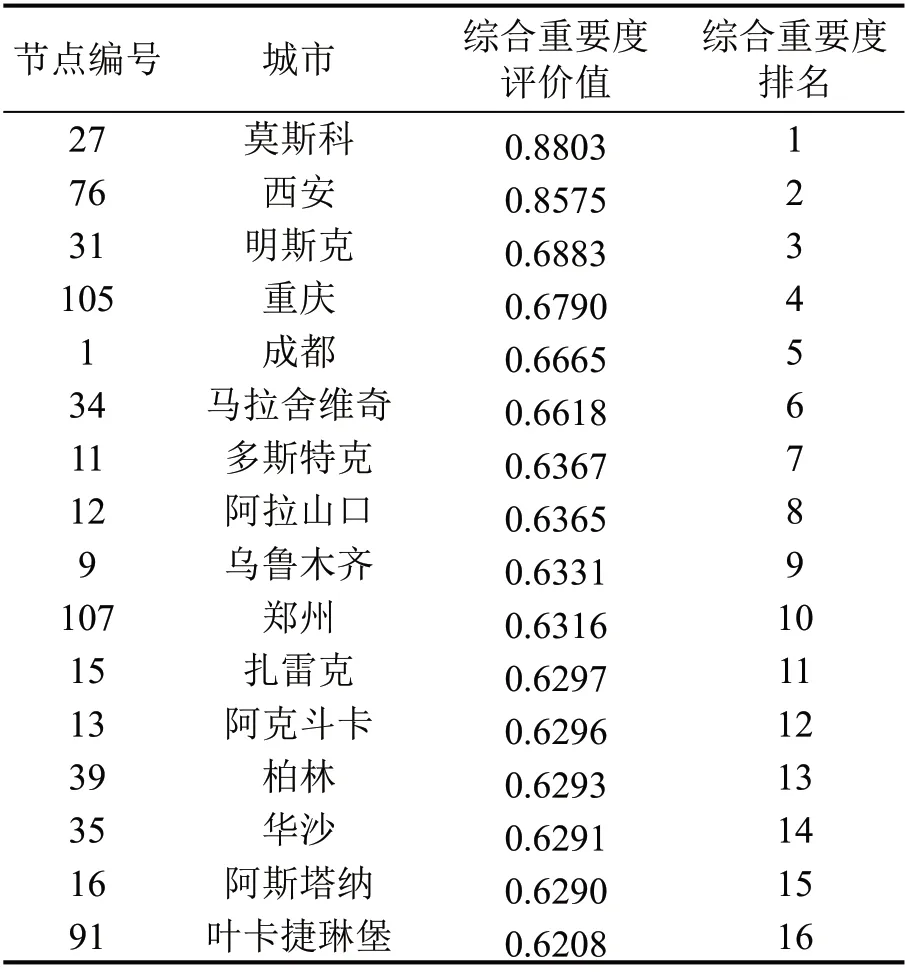
表2 中欧班列运输网络节点重要性排名(前10%)Table 2 Ranking of node importance of CR express transportation network(top 10%)

3.4 节点重要性分析

从国家层面看，中欧班列运输网络中前10%的重要节点主要分布于中国、哈萨克斯坦、俄罗斯、白俄罗斯、波兰及德国，这些节点在中欧班列运输网络中具有重要的地位，为了保障中欧班列的平稳运行，提高中欧班列运输网络的鲁棒性，有必要保护上述关键节点。

以中国为例，中国境内的关键节点有6 个，分别为西安、重庆、成都、阿拉山口、乌鲁木齐以及郑州。其中，阿拉山口是我国西北地区最大的陆路边境口岸，多个城市开行的中欧班列均需通过阿拉山口出境，随着中欧班列开行数量的增加，阿拉山口节点需要继续加强基础设施建设，增加换装线及到发线，同时，应加快班列通关速度，避免节点因拥堵造成瘫痪。境内其他节点为国家发展和改革委员会支持的五大中欧班列集结中心示范工程建设。重庆和成都作为国内较早开行中欧班列的城市，是中欧班列主要的货源和开行城市。西安、乌鲁木齐和郑州凭借优越的地理位置，已经发展成为我国重要的中欧班列枢纽城市。以上5 大节点应继续发挥枢纽作用，在国家政策的推动下，加强基础设施建设，加快构建高效运输组织体系，推动中欧班列的高质量发展。

哈萨克斯坦境内的关键节点有4个，分别为多斯特克、扎雷克、阿克斗卡和阿斯塔纳，均属于中欧班列开行线路中重要的途径城市。这与俄乌冲突时代的中欧班列发展趋势相吻合，中欧班列南通道的快速发展使哈萨克斯坦在“一带一路”运输网络中承担的地位愈发重要，庞大的货运流量为其节点的运输带来巨大压力。哈方应加强对这些节点的维护，加快国际物流园区建设，简化通关流程，缩短通关时间。

俄罗斯境内的关键节点有2个，分别为莫斯科和叶卡捷琳堡。叶卡捷琳堡作为西伯利亚铁路中的重要枢纽城市，连接多个节点城市。莫斯科作为俄罗斯的首都，拥有优越的地理条件，也是多条中欧班列线路的终到城市。为提高中欧班列运输网络的鲁棒性，建议俄罗斯加强基础设施维护，避免因线路和设备老化造成节点瘫痪，同时，改善线路条件，例如，对西伯利亚大铁路和贝加尔湖-阿穆尔河干线进行维护。

3.5 方法有效性验证

为证明本文提出的基于改进TOPSIS法及灰色关联分析的多层网络节点重要性评价方法的有效性，挑选BC算法、DC算法和PageRank算法识别中欧班列运输网络的重要节点。利用多层网络SIR模型模拟节点传播过程对方法进行对比验证，以判断关键节点受到影响后对全局运输网络的影响。不同方法计算的中欧班列基础路网和中欧班列车流网络排名前10%的节点如表3所示。

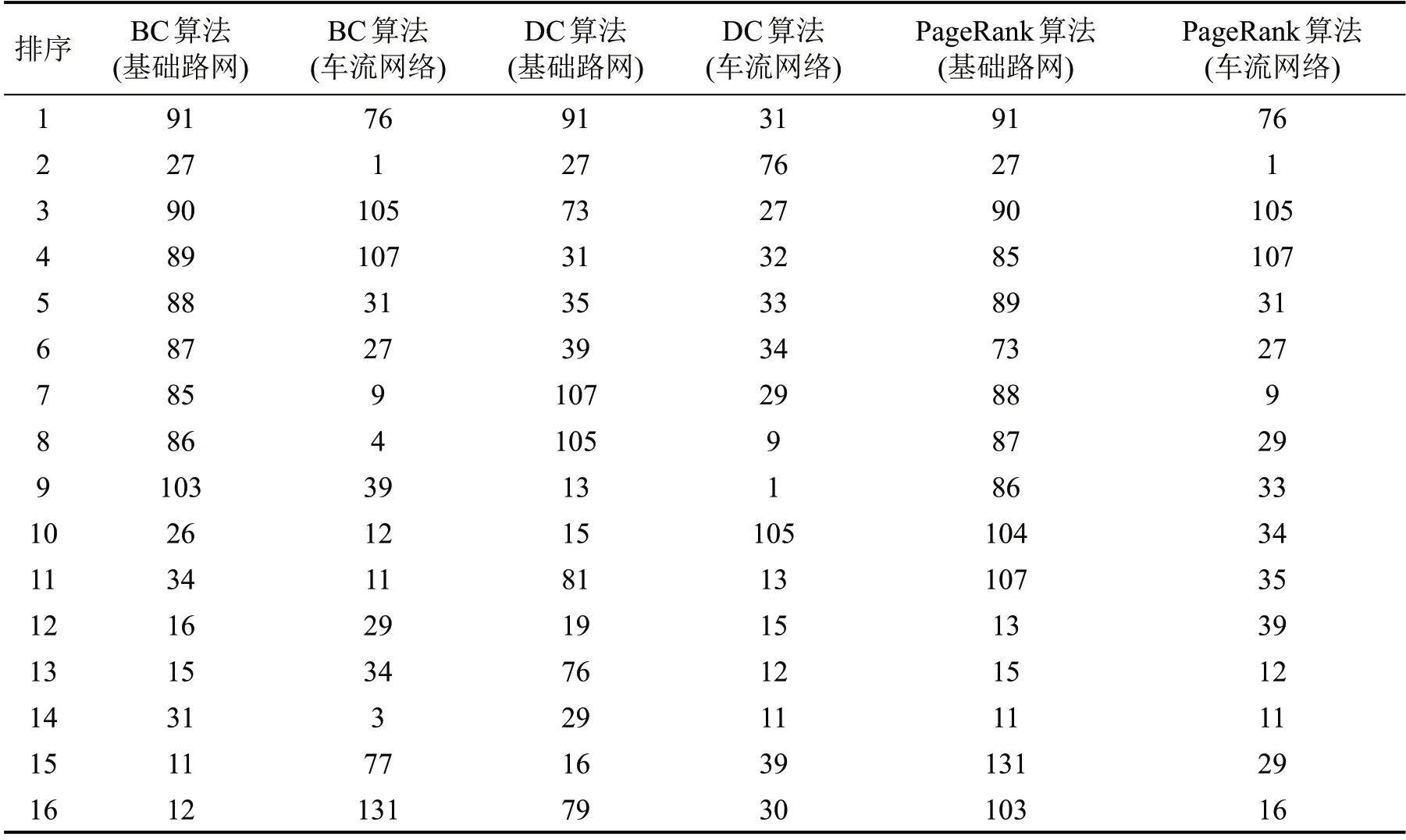
表3 中欧班列运输网络关键节点排序统计表(前10%)Table 3 Statistical table of ranking of key nodes in CR express transportation network(top 10%)

由表4 可知，总体而言，各关键节点识别方法对同一网络层的关键节点识别结果相差不大，只有部分节点不同，此外，同一节点在不同的识别方法中排序不同。在不同网络层中，同一关键节点识别方法的识别结果存在较大的差异，主要是因为不同网络层的结构及连边属性不同。

在运用多层网络SIR模型的过程中，需要考虑双层网络是存在一定的联系，故若2个节点在不同的网络层中均存在连边，则代表2个节点之间的传播途径增加，因此，这2 个节点之间的传播概率会有所增加[15]。多层网络SIR模型传播过程如图5所示。若节点m、n在G(1 )、G( 2 )这2个网络层上均有联系，α、β分别为2 个单层网络中的传染病传播概率，则在多层网络中，节点m与节点n之间的传播概率为γ=1-(1 -α)(1 -β)。

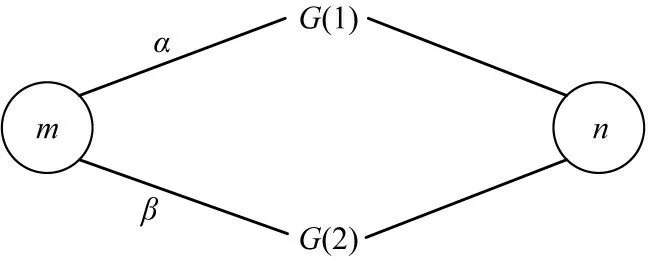
图5 多层网络SIR模型传播过程Fig.5 Propagation process of multi-layer network SIR model

将各关键节点识别方法得到的前10%的关键节点作为初始感染节点，利用多层网络SIR模型进行验证，由于多层网络传播概率不能设定太大，设定中欧班列基础路网与车流网络中的传播概率均为0.05，恢复率为1，如果2节点在中欧班列基础路网和车流网络中都存在连边，则传播概率为0.091。计算直到网络中所有节点均无法被感染时，感染节点与恢复节点占总节点数量的比例，由于节点感染以概率方式进行，因此，取50次独立实验结果的平均值作为评价结果。各SIR 传播曲线如图6所示。

图6 各关键节点识别方法所得前10%的节点作为初始传染源节点时的SIR传播曲线Fig.6 SIR propagation curve when first 10%of nodes obtained by each key node identification method are used as initial infection source nodes

由图6 可知，一方面，由于不同识别方法对同一网络层之间关键节点识别结果相差不大，因此，传播曲线较为接近；另一方面，在不同网络层中，由于网络结构和连边属性存在差异，导致评价结果存在一定差异，传播曲线图表明车流网络中的重要节点对中欧班列运输网络影响更大。从整体来看，以本文所提出的TOPSIS-GRA 关键节点识别方法得到的关键节点作为初始感染节点时，在多层网络SIR传播模型中的传播速率最快，网络感染率在迭代20 次后达到97.8%，30 次后接近峰值便趋于稳定。由此可以发现，本文所提出的关键节点识别方法得到的关键节点对全局网络的影响更为普遍和高效，亦印证了方法的优越性和有效性。同时，多层网络的融合评价提高了节点识别的准确率。以成都和重庆为例，均位于中欧班列基础路网的外层，在基础路网层中的重要度排名较低，但成都和重庆作为较早开行中欧班列的城市以及枢纽城市，在车流网络层中的重要度评价值较高，因此，需要综合评价其在中欧班列运输网络中的地位。由此可见，从单一层面评价节点重要性，可能会导致评价结果失真。

4 结论

本文考虑中欧班列的多层复杂网络性质，提出一种基于改进TOPSIS法及灰色关联分析融合算法的节点重要度评价方法，研究了中欧班列运输网络中的关键节点识别问题。同时，本文在实例分析中利用多层网络SIR 模型与传统网络排序方法进行比较分析，验证本文提出方法的有效性。实例分析结果表明，网络中排名前10%的重要节点一部分集中在中欧班列主要线路的起讫城市和主要集结中心，例如西安、重庆、成都、郑州、乌鲁木齐以及波兰的华沙、俄罗斯的莫斯科等；另一部分则集中在境内外主要口岸，例如阿拉山口和波兰的马拉舍维奇等。同时，研究得到的多斯特克、扎雷克、阿克斗卡和阿斯塔纳这4 个关键节点均位于哈萨克斯坦境内，符合俄乌冲突时代背景下中欧班列南向通道愈发重要的发展趋势。识别的关键节点与实际情况和国家规划较为契合。经过对方法的有效性验证发现，采用本文提出方法识别出的排序前10%重要节点作为初始感染节点，网络感染率在20 次迭代后达到97.8%，网络节点感染率及传播速率均高于BC 算法、DC 算法和PageRank 算法等单一网络排序方法，即识别的关键节点对全局网络的影响更为普遍和高效，而单层网络识别容易出现评价结果失真现象。