基于生存分析的山区双车道公路超车持续时间模型

戢晓峰，戴秉佑，普永明，郝京京

(昆明理工大学，a.交通工程学院；b.云南省现代物流工程研究中心，昆明 650500)

0 引言

山区双车道公路具有无中央分隔栏，弯道多且半径小，接入口密度大，穿越村镇路段占比高及路侧防护设施缺乏等特征，行车环境复杂，交通事故频发。据云南省公路局长期监测数据，云南双车道公路的货车混入比例高达15%，同时，在我国山区双车道公路途径的农村地区，摩托车是主要的出行方式[1]。低速货车或摩托车混入后常导致后车无法达到期望速度，由此引发后车频繁换道和超车，在无中央分隔栏的双车道上超车是极为复杂和危险的驾驶行为，后车驾驶人往往需要占用对向车道完成超车，超车持续时间常被用来表征驾驶人暴露在极端危险情况下的时长[2]，是评价双车道公路交通安全的重要指标。如何获得混合交通流条件下山区双车道公路超车持续时间分布，确定关键影响因素与超车持续时间之间的关系，提升山区双车道公路交通安全，已成为亟需解决的重大现实问题。

随着数据采集与驾驶模拟技术的发展，双车道公路超车行为逐渐成为国内外学者研究热点。HEGEMAN 等[3]通过自然驾驶开展实车实验，采集了荷兰农村双车道公路48 次超车行为，分析不同超车策略和车速下超车持续时间的差异。GRAY等[4]利用驾驶模拟器研究驾驶员的超车策略和决策，发现某些情况下即使无足够时间完成超车，但当对向车辆距离高于临界值时，驾驶员仍会选择超车。VLAHOGIANNI 等[5]利用驾驶模拟器采集了不同性别驾驶人的超车行为，分析性别、速度差及是否多次进行超车等因素对双车道超车持续时间的影响。ASAITHAMBI等[2]通过移动跟车法，分析印度混合交通流条件下城市双车道公路各类型车辆的超车特性。BELLA 等[6]利用装有摄像头和GPS的摩托车，采集了罗马城郊双车道公路摩托车101 次超车行为，并基于生存分析建立了摩托车超车持续时间模型。MOLL等[7]分析了超自行车的持续时间对农村道路安全和交通运行的影响，建立了超自行车的持续时间贝叶斯预测模型。当前，已有研究主要集中于发达国家同质交通流条件下的农村双车道公路或发展中国家混合交通流条件下的城市双车道公路的超车行为，对我国混合交通流条件下山区双车道公路超车行为的研究较为鲜见。同时，数据采集主要通过自然驾驶和驾驶模拟器，自然驾驶实验通常仅能获取实验车辆的精确数据，较难获取参与超车过程的其他车辆的精确数据，且需较多实验参与者；驾驶模拟器可在安全的实验环境中采集不同驾驶员对不同情况的超车行为，但LLORCA 等[8]也指出较实测数据，驾驶员在驾驶模拟器中超车持续时间更短，且横向偏移更大。

因此，本文尝试利用无人机采集混合交通流条件下山区双车道公路超车行为视频数据，提取参与超车行为的机动车轨迹，构建超车行为变量指标体系，分析山区双车道公路超车行为特性，建立基于生存分析的山区双车道公路超车持续时间模型，确定影响超车持续的关键协变量，并分析关键协变量与超车持续时间之间的定量关系。研究尝试为山区双车道公路交通安全改造，微观交通流仿真模型构建和开发先进双车道超车辅助系统提供参考。

1 数据采集与提取

1.1 数据采集

本文选取云南省典型的山区双车道公路——元双公路牟定段为研究对象，开展数据采集工作。研究路段地处云南高原中北部，全长87.42 km，设计速度60 km·h-1，路基宽7.5 m，为双向两车道，路面均为改性沥青混凝土路面。经多次实地观测发现，山区双车道公路超车行为多发生于平直路段，可能是由于组合和弯道路段无法满足驾驶员的超车视距导致。为尽可能多采集山区双车道公路超车行为，避开穿村镇路段、长大下坡路段和交叉口等特殊路段的影响，本文选取元双公路平直路段K57+100～K57+600作为研究路段，如图1所示。路段基本信息如表1所示。

采用无人机高空录像进行原始数据采集，采集时间为天气晴朗的工作日。无人机高空录像时将视频分辨率调至2 K，拍摄高度控制175 m，尽量避免树木和建筑等遮挡，以保证航拍效果。

1.2 超车行为变量提取

为识别影响超车持续时间的关键因素，本文通过分析山区双车道公路超车行为，提取超车过程中的变量。在CHOUDHARI 等[9]和BELLA 等[6]研究基础上，将超车行为划分为3个阶段，如图2所示。

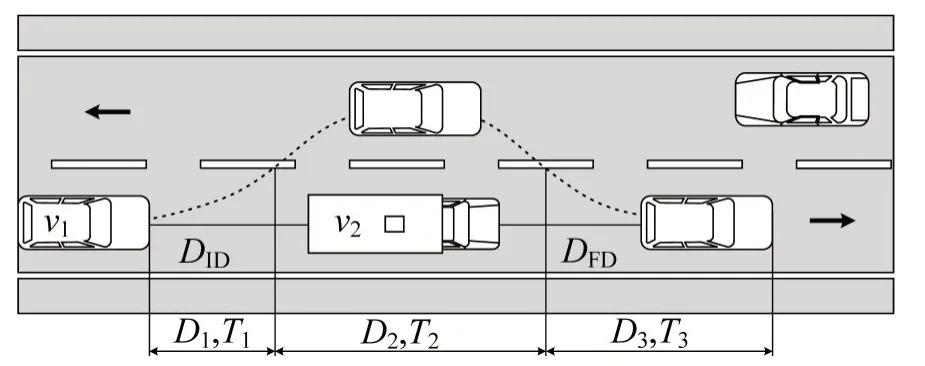
图2 超车行为的阶段和变量Fig.2 Phases and variables of overtaking maneuver

(1)换道阶段，从超车车辆开始产生超车意图的时刻开始，到越过道路中心线的时刻停止。

(2)占道超车阶段，超车车辆占用对向车道完成超车。

(3)并道阶段，从超车车辆越过道路中心线返回右车道的时刻开始，到超车车辆结束超车行为时停止。

结合超车行为相关研究文献[7]，山区双车道公路的混合交通流特性，以及数据采集处理的难易程度这3 个方面，最终选取超车车辆初始速度、被超车车辆初始速度、超车车辆与被超车车辆的初始速度差、被超车车辆长度、是否有对向车等指标构建山区双车道公路超车行为变量指标体系，如表2所示。利用George 软件[10]提取路段上参与超车行为的机动车轨迹数据，进而提取超车行为变量，轨迹精度为0.1 m，时间粒度为0.12 s，数据精度可应用于超车行为分析。

表2 超车行为变量Table 2 Variable of overtaking maneuver

2 生存分析模型

2.1 超车持续时间生存分析

生存分析是一种将事件的结果和事件所经历的时间结合起来分析的现代统计方法。将生存分析应用到超车持续时间分析中，对应的要素定义如下。

(1)超车行为的生存时间。该生存时间定义为超车行为的持续时间，即超车行为开始到超车行为结束所经历的时间。

(2)超车行为的生存函数S(t)。令T为超车行为持续时间的非负随机变量，令f(t)为T的概率密度函数，T的分布函数为

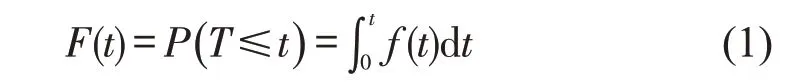
超车行为的生存函数S(t)被定义为超车行为持续时间大于t的概率，即

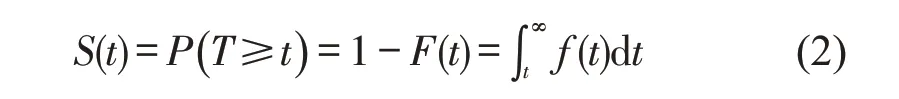
(3)超车行为的危险函数h(t)。超车行为的危险函数h(t)指超车行为在持续了t时间后仍没有结束，但在接下来的t至t+Δt时间内结束的概率，即

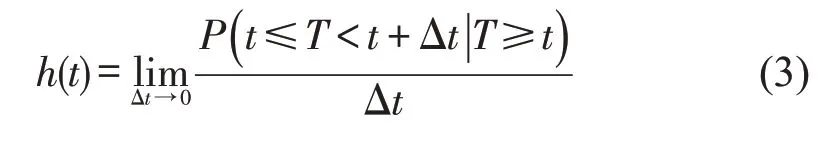
由条件概率可得

求解微分方程可得

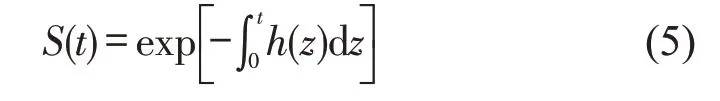
2.2 基于参数生存模型的超车持续时间建模

生存分析模型可划分为非参数、半参数和参数模型。非参数模型常被用于分析单变量生存数据，具有无需对生存时间的分布做出假设的优点，但无法量化协变量的影响程度，模型可解释性差。半参数模型中使用最为广泛的是比例风险回归模型(COX model)，该模型以生存结局和生存时间为因变量，可同时分析多因素对生存时间的影响，但COX 模型假定协变量取不同值时，风险是成比例的，与时间没有关系，这与实际超车行为不符。参数模型在危险函数服从某种特定的参数分布时具有更好的效果，加速失效时间模型(Accelerated Failure Time model,AFT model)是一种常用的参数模型，其数学形式简单易于理解，同时具有较强的可解释性。

考虑到模型的可解释性和实际中超车行为的危险率可能更符合某种参数分布，本文引入加速失效时间模型，识别影响超车持续时间的关键因素和具体影响程度。令exp(βX)为协变量，加速失效时间模型为

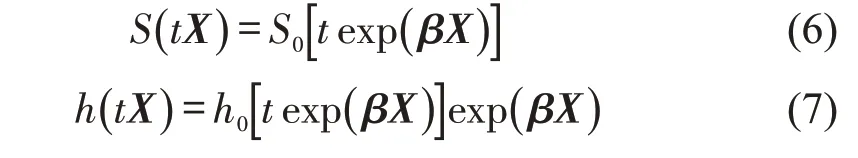
式中：S0、h0分别为标准生存函数、标准危险函数；X为协变量组成的向量；β为协变量系数组成的向量。

AFT模型可线性表示为

式中：ε为随机误差项。

危险函数形式通常基于理论分析或统计分析结果进行选择。为寻找最适合山区双车道公路超车持续时间的危险函数形式，本文尝试针对常用分布形式进行对比分析，使用赤池信息准则(The Akaike's Information Criterion,AIC)和贝叶斯信息准则(Bayesian Information Criterion,BIC)评估不同分布形式的参数模型性能，AIC 值和BIC 值越小，代表模型的效果越好。

经比较后，确定Log-logistic分布为山区双车道超车持续时间的最优分布形式，Log-logistic分布由尺度参数λ和形状参数γ控制。如果γ＞1，则其危险函数单调递减；如果0＜γ＜1，则其危险函数先增加直到最大值之后，渐近减小到0。其生存函数S(t)和危险函数h(t)分别为

3 结果分析

3.1 超车持续时间描述性统计

山区双车道公路超车持续时间协变量描述性统计如表3所示，由于超多辆车的驾驶行为样本量较小，本文仅针对超单车行为展开分析，记录76次超车行为。

表3 超车持续时间协变量描述性统计Table 3 Descriptive statistics of overtaking duration

由表3可知，山区双车道公路的平均超车持续时间为10.3 s，平均超车距离为201.3 m，远高于ASAITHAMBI 等[2]在印度双车道公路混合交通流情况下所得到的公路平均超车持续时间7.5 s，平均超车距离101.6 m。同时，较MOCSARI等[11]在西班牙双车道同质交通流情况下所得到的平均超车持续时间8.3 s 更大(一般而言，同质交通流条件下两车速度差较小，超车持续时间更长)，原因是驾驶员的驾驶风格、较高的行驶速度以及复杂的交通流条件共同作用所致。

①本土驾驶员的超车意图更强烈，超车行为发生的更早，超车车辆与被超车车辆的平均初始间距为23.8 m，几乎为LLORCA等[12]在西班牙双车道公路研究中发现的初始间距平均值13 m 的2 倍。同时，超车车辆在超越被超车车辆后，由于车速较快，驾驶员为获得更好的视野和驾驶感受，在无对向车的情况下，不愿立即返回原车道，超车车辆与被超车车辆的平均最终间距为30.4 m，远大于BELLA 等[6]在意大利双车道公路所得的9.2 m，这是山区双车道公路超车持续时间更长的主要原因。

② 被超车和超车车辆初始速度分别为55.6 km·h-1和67.2 km·h-1，均接近或大于公路的设计速度，尽管超车车辆与被超车车辆的初始速度差较大，为11.6 km·h-1，但值得注意的是标准差高达12.9 km·h-1，表明有相当一部分车辆开始超车时，速度与被超车车辆接近，超车车辆的加速性能参差不齐，且被超车车辆多为货车(平均被超车车辆长度为6.8 m)，这些因素共同作用使得山区双车道公路超车持续时间更长。

山区双车道公路超车持续时间分布如图3所示。

图3 超车持续时间分布Fig.3 Distribution of total overtaking duration

由图3 和表3 可以发现：32.4%的超车行为在9 s内结束，对视频数据进行分析发现，这类超车行为主要发生于客车超摩托车或超车过程中有对向来车时(第1类超车)。

(1)客车超摩托车的平均持续时间约为7.5 s，摩托车的平均初始速度约为48 km·h-1，客车的平均初始速度约为72 km·h-1，初始速度差Δdv高达24 km·h-1，且摩托车体积小，在双车道公路上更倾向于贴近路侧行驶，使客车能占用较少的对向车道快速完成超车。平均最大横向距离仅为3.1 m，对于客车驾驶员而言，超摩托车的驾驶行为与避开障碍物的驾驶行为类似，因而，驾驶员极有可能在有对向车的情况下仍选择超车(在11次客车超摩托车中，2次有对向来车时超车)。

(2)在有对向来车的超车中，平均超车持续时间约为7.9 s，换道阶段用时为1.5 s，占道超车阶段用时为5.2 s，并道阶段用时为1.2 s，占道超车阶段用时明显降低，说明有对向车时，驾驶员能感知到较高的风险，迫使其完成超越后立即返回原车道。62.2%的超车行为结束于9～14 s 间，这类超车行为主要发生于货车超摩托车或客车超客车、货车时(第2类超车)。

(3)货车超摩托车的平均持续时间约为12.6 s，换道阶段用时为3.4 s，占道超车阶段用时为6.9 s，并道阶段用时为2.3 s。由于货车的体积较大，机动性差，导致换道和并道阶段用时较长，货车的平均初始速度约为58 km·h-1，摩托车的平均初始速度约为40 km·h-1，货车驾驶员超摩托车时较客车驾驶员更为谨慎，超车过程中均无对向车辆，且超车过程中与摩托车保持了较大的横向间距(平均最大横向距离为4.3 m)。

(4)客车超客车、货车是山区双车道公路最常见的超车行为，平均超车持续时间约为11.7 s，换道阶段用时为1.8 s，占道超车阶段用时为8.5 s，并道阶段用时为1.4 s，在52 次客车超客车、货车中，有13次有对向来车时超车，客车的超车行为表现出较强的异质性，可能是车辆性能与驾驶员风格差异所致。5.2%的超车行为持续时间大于14 s，这类超车行为主要发生于货车超客车、货车时(第3类超车)。

(5) 货车超客车、货车的平均持续时间约为15.2 s，换道阶段用时为3.3 s，占道超车阶段用时为9.5 s，并道阶段用时为2.4 s，平均最大横向距离为4.2 m，超车过程中仅有1 次有对向车辆，表明货车驾驶员更注重超车时机选择和横向距离保持。

3.2 基于参数生存模型的超车持续时间分析

本文利用python 语言构建参数生存模型。超车行为涉及的协变量较多，若模型未考虑对超车持续时间影响显著的协变量，将导致所建立的模型性能差，不能反映实际超车持续时间；若模型包含的协变量过多，则会引入无关变量，使得模型可解释性降低。因此，为找到具有统计学意义的协变量与最优参数模型，本文通过两步实现：首先，固定模型参数分布形式，采用向后逐步回归法筛选显著的协变量，获得该分布下的最优协变量组合；然后，利用AIC 和BIC 评价各参数分布形式下最优模型的性能，找到最适合于山区双车道公路超车持续时间的参数分布和协变量组合。

分别选择Weibull 和Log-logistic 分布进行试验，对表2 中协变量建立加速失效时间模型，每步回归中，似然比检验水平设置为0.05，经过多次试验后，得到最优的加速失效时间模型以及具有统计学意义的协变量。Log-logistic和Weibull加速失效时间模型估计结果如表4和表5所示。

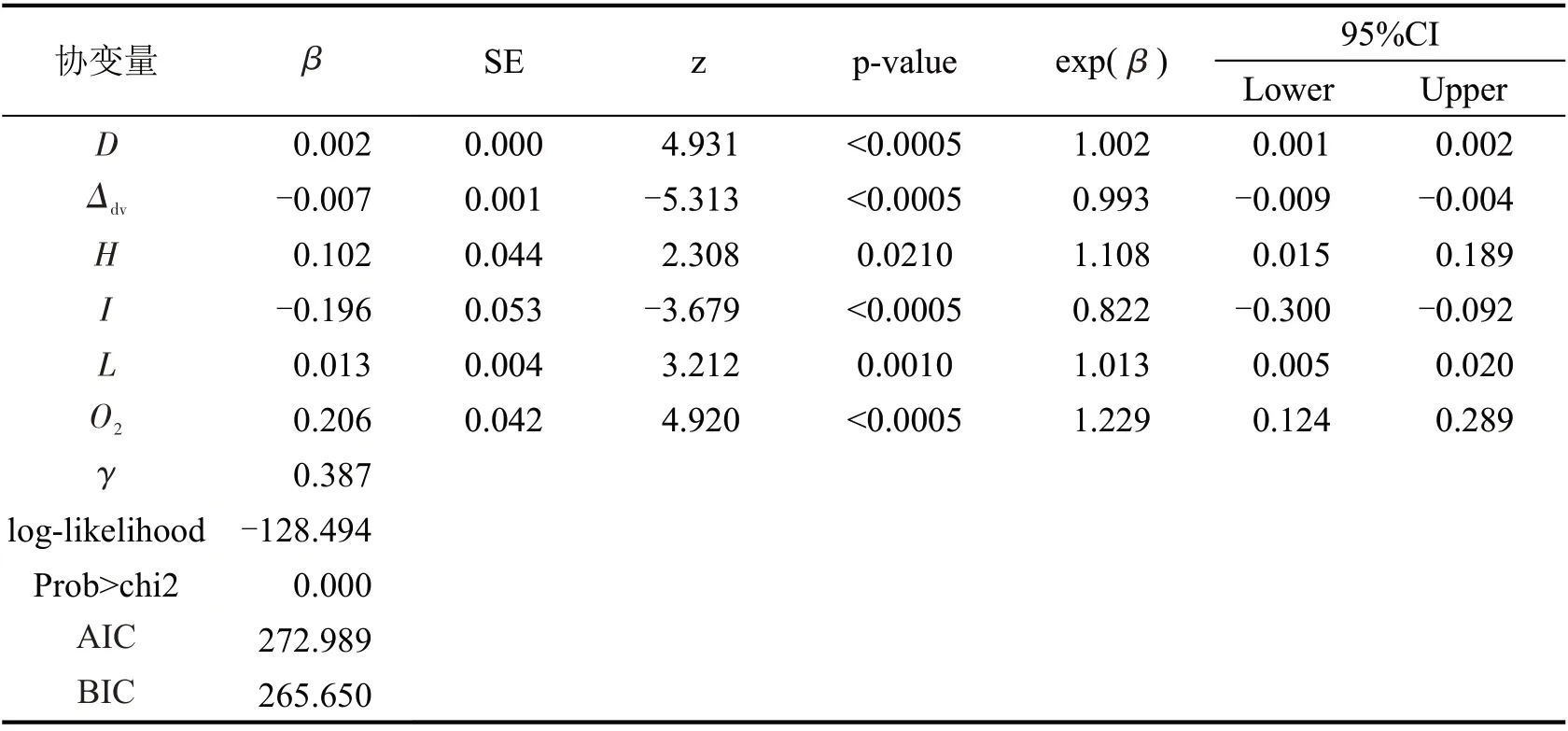
表4 Log-logistic加速失效时间模型估计结果Table 4 Estimates of Log-logistic AFT model

Log-logistic AFT 模型的对数似然函数估计值为-128.494，Weibull AFT模型的对数似然函数估计值为-131.511，表明Log-logistic AFT模型的结果略优于Weibull AFT 模型。Log-logistic AFT 模型的AIC 和BIC 分别为272.989 和265.650，Weibull AFT模型的AIC 和BIC 分别为279.021 和271.682，AIC和BIC 较Weibull AFT 模型均降低了2.2%，进一步表明Log-logistic AFT 模型的拟合度更好。生存函数S(t)和危险函数h(t)分布如图4所示。

图4 生存函数和危险函数分布Fig.4 Survival Function and Hazard Function

Log-logistic AFT 模型形状参数γ的估计值为0.387，危险函数随时间的增加而增加直至最大值(拐点)，约为13 s，然后逐渐减小，说明在拐点之前超车行为结束的可能性逐渐升高，在13 s时达到最高，之后慢慢降低，降低的原因可能是货车加速超越客车、货车且没有对向来车迫使其结束超车。所获得的危险函数分布形式与VLAHOGIANNI[5]通过驾驶模拟器所获得的危险函数分布相似，但危险函数的拐点(13 s)约为其获得的危险函数(7 s)的2倍。

通过分析表4可知：

(1)Log-logistic AFT模型确定了影响超车持续时间的6个具有统计学意义的协变量，分别为超车距离D，超车车辆与被超车车辆的初始速度差Δdv，最大横向距离H，是否有对向车I，被超车车辆长度L和超车车辆类型O2。参数估计值β反映了协变量的影响方向与程度，其中，超车距离D、最大横向距离H、被超车车辆长度L和超车车辆类型O2的参数估计值β均大于0，说明其增加将使超车所需的时间增加，而超车车辆与被超车车辆的初始速度差Δdv与是否有对向车I的参数估计值小于0，说明其增加将使超车所需的时间减少。

(2) 协变量的影响程度可通过危险比exp(β)表示，协变量每增加或减少1 个单位，将增加或减少预期超车持续时间的exp(β)-1个百分比。影响程度最大的协变量为超车车辆类型O2，当超车车辆类型为货车时(O2=1)，超车持续时间增加了22.9%。货车受限于其机动性差，车辆尺寸和载重大，其超车所需时间更长。同时，营运货车驾驶人由于受工作倦怠和情绪等多重因素影响[13]，导致其表现出较激进的驾驶风格，尽管其更注重超车时机的选择，但涉及货车超车的事故一般严重程度更高，仍是需要重点关注的超车行为。其次，是否有对向车I对超车持续时间的影响较大，当有对向车时(I=1)，超车持续时间降低了17.8%。

(3) 最大横向距离H每增加1 m，将会使超车持续时间增加10.8%，超车车辆的最大横向距离减小会降低换道和并道所需的时间，使得超车持续时间减少。被超车车辆长度L每增加1 m，将会使超车持续时间增加1.3%。超车距离D和超车车辆与被超车车辆的初始速度差Δdv的影响较小，分别为0.2%和-0.7%，然而，如果考虑协变量的平均值，超车距离D和最大横向距离H的平均影响较大，分别为0.2%×201.3=40.3%和10.8%×3.8=41%，超车车辆与被超车车辆的初始速度差Δdv和被超车车辆长度L的平均影响较小，分别为11.7×(-0.7%)= -8.2%和6.8×1.3%=8.8%。

4 结论

(1)混合交通流条件下，山区双车道公路的平均超车持续时间为10.3 s，平均超车距离为201.3 m，远高于同质交通流条件下农村双车道公路或混合交通流条件下城市双车道公路，究其原因是驾驶员的驾驶风格、较高的行驶速度以及复杂的交通流条件共同作用所致。

(2)山区双车道公路的超车行为可根据持续时间分为3 类，第1 类超车主要发生于客车超摩托车或超车过程中有对向来车时，通常在9 s内结束；第2 类超车主要发生于货车超摩托车或客车超客车、货车时，通常结束于9～14 s 间；第3 类超车主要发生于货车超客车、货车时，通常结束于14～16 s间。

(3)Log-logistic AFT模型对超车持续时间拟合效果最好，AIC和BIC分别为272.989和265.650，危险函数的拐点约为13 s，说明超车行为在13 s 前结束的可能性最大。影响超车持续时间的关键变量分别为超车距离，超车车辆与被超车车辆的初始速度差，最大横向距离，是否有对向车，被超车车辆长度和超车车辆类型。影响程度最大的协变量为超车车辆类型，当超车车辆类型为货车时，超车持续时间增加了22.9%；其次，是否有对向车对超车持续时间的影响较大，当有对向车时，超车持续时间降低了17.8%；超车距离和超车车辆与被超车车辆的初始速度差的影响较小，分别为0.2%和-0.7%。