基于动态分流元胞传输模型的城市道路网络韧性评估
吕彪,谢智宇,康宇翔,赵雨萌
(西南交通大学,信息科学与技术学院,成都 611756)
0 引言
城市道路网络是维系城市正常运转的核心基础设施。由于城市道路网络开放运行,加之人、车、路及环境之间存在复杂交互作用,当发生地震和暴雨等自然灾害以及严重交通事故和人为蓄意破坏等重大扰动事件时,很容易造成事发区域路网性能严重退化和服务水平明显下降。因此,准确评估潜在重大扰动事件下城市道路网络性能,并以此为依据制定应对方案,对于维持路网稳定运行具有重要意义。
现有研究通常使用可靠性、脆弱性及鲁棒性等指标描述扰动事件下的路网性能。可靠性通常以概率测度扰动事件下路网维持预期性能的能力;脆弱性侧重描述扰动事件对路网性能可能造成的不利后果;鲁棒性强调扰动事件下路网性能偏离预期水平的程度[1]。上述指标分别从不同侧面或维度描述扰动事件下的路网性能,适合作为常态扰动事件下路网性能测度指标。然而,面临重大扰动事件时,交通管理者和出行者不仅关心路网达到预期性能的概率或可能遭受的不利后果以及偏离给定阈值的程度,同时,关心一旦偏离稳态后如何快速有效恢复正常。
在此背景下,研究者引入韧性作为重大扰动事件下交通系统性能测度指标[1]。韧性是一个多维度综合性指标,其核心内涵包括两方面:一是抵御扰动能力,通过扰动事件后系统偏离正常性能的程度体现;二是快速恢复到预期性能的能力[1]。现有研究主要围绕交通系统韧性定义、评估与优化等方面开展研究。在韧性定义方面,MURRAY-TUITE等[2]首次提出了交通系统韧性的概念,指出交通系统韧性包括:适应性、移动性、安全性以及快速恢复性等10个方面;TWUMASI-BOAKYE等[3]认为韧性是一种复合能力,有韧性的系统是遭受扰动时失效概率低,吸收事件扰动能力强(脆弱度低)及恢复速度快的系统;FATURECHI等[4]将交通系统韧性定义为扰动事件下系统出行时间与正常条件下系统出行时间比值的倒数;HENRY等[5]将韧性定义为恢复期内系统性能恢复程度与扰动事件造成的系统性能损失程度的比值。在韧性评估方面,TESTA等[6]使用聚类系数和平均节点度作为韧性测度指标;TWUMASI-BOAKYE 等[3]从鲁棒性、冗余性、资源充足性及恢复快速性等4 个方面评价路网韧性;ZHANG 等[7]以拓扑效率为路网性能指标,以扰动事件后路网性能损失程度为韧性指标;张洁斐等[8]以拓扑效率为路网性能指标,以扰动事件后路网拓扑效率累积损失程度为韧性指标;吕彪等[9]提出了考虑线路流量影响的路网服务效率指标和基于服务效率的路网服务韧性指标。在韧性优化方面,CHEN 等[10]研究了多式联运系统中以提升韧性为目标的路网修复问题;FATURECHI等[4]研究了道路交通系统中以提升韧性为目标的路网修复问题;张洁斐等[8]提出基于韧性评估的地铁网络修复时序方案;吕彪等[9]提出以路网服务韧性最大化为目标的优化模型,并基于遗传算法求解模型,获得最优恢复策略。
综合来看,目前,关于交通系统韧性的研究尚处于起步阶段,已有的少量研究重点从路网拓扑结构角度设计韧性指标,鲜有研究考虑扰动事件下的出行决策行为变化,以准确预测路网流量分布状态及演化规律为基础构建韧性指标[1]。实际城市道路网络中,当面临地震和暴雨等重大扰动事件时,可能并未出现路段完全中断等极端情形,因此,路网拓扑结构指标并未出现变化,但扰动事件极易造成部分路段通行能力显著下降,进而影响出行决策行为,造成选择受影响路段的出行者明显减少。因此,针对城市道路网络开展韧性评估必须考虑扰动事件下出行决策行为影响以及由此导致的流量分布状态变化。
如何准确预测扰动事件下路网流量分布状态及演化规律?已有研究大多使用解析方法,通过合理假定出行决策行为,基于用户均衡(User Equilibrium, UE)、随机用户均衡(Stochastic User Equilibrium, SUE)或动态配流(Dynamic Traffic Assignment,DTA)等原则构建数学模型,进而获得路网流量分布状态。解析方法强调数学推理的严密性,但忽略了车辆等微观个体面对实际交通条件的应激性反应,无法描述实际车流中普遍存在的激波和排队等现象,无法真实模拟实际交通流动力学特性。尤其在发生重大扰动事件后,路网交通流形态可能出现更复杂的特征。为应对解析方法的不足,元胞传输模型(Cell Transmission Model, CTM)等仿真方法因能准确模拟交通流动态特性,揭示实际交通流的运行机理与演化规律,正广泛用于动态交通分配和交通系统优化等领域。需要指出的是,传统元胞传输模型无法直接应用于重大扰动事件下的交通流仿真。原因在于,重大扰动事件造成的影响通常持续数日乃至数周,在此期间,出行者可能会根据出行条件的变化频繁调整出行路径,从而造成交通流逐日(day-to-day)显著波动。例如,911事件和伦敦地铁恐怖袭击事件等均造成事发后一段时间内受影响区域交通流明显波动。而现有元胞传输模型重在描述交通流在不同元胞间的传输过程,未建立起与交通流逐日波动演化过程的耦合关系。例如,现有元胞传输模型通常将交叉口分流比例设置为常数,意味着流量在不同路径间的分布比例是恒定不变的,显然不符合重大扰动事件下的路网实际。
基于上述分析,本文以韧性作为重大扰动事件下城市道路网络性能测度指标,明确考虑扰动事件下基于认知更新的出行决策行为,提出一种考虑路径流量逐日变化的动态分流元胞传输模型,并以路网效率为基础性能指标,构建可全面评价扰动事件影响期内路网效率动态累积变化的韧性指标与评估模型,并使用Sioux Falls网络进行算例分析。
1 动态分流元胞传输模型
1.1 模型构建
元胞传输模型于1994 年由DAGANZO[11]首次提出。CTM 是对以流体动力学理论为基础的LWR (Lighthill-Whitham-Richards)宏观交通流模型[12]的离散化近似,其基本原理是:将路段划分为若干首尾相连的元胞,在满足流量守恒和容量限制等条件下,计算元胞输入和输出交通量,并根据一定时间步长迭代更新元胞状态,获得元胞动态交通特征指标。CTM 以近似梯形的宏观基本图为依据,假设交通流率q与交通密度ρ满足关系[11]为
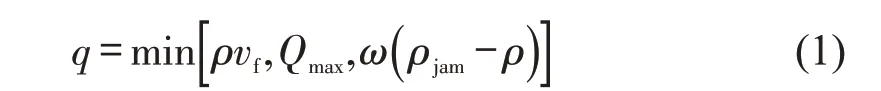
式中:vf,ω,ρjam,Qmax分别为自由流速度、交通拥挤时反向激波速度、阻塞密度及最大流率。
由于DAGANZO 提出的CTM 存在一些不足,后续研究分别考虑交通流迟滞现象[13]、元胞可变长度[14]及交叉口信号控制[15]等因素进行了改进。但需要特别指出的是,现有元胞传输模型[15]重在描述交通流在不同元胞间的传输过程,未考虑元胞流量传输与路径流量动态变化之间的耦合关系,因此,无法直接应用于重大扰动事件下的交通流仿真。
为弥补现有模型的不足,在已有研究成果基础上,本文提出一种动态分流元胞传输模型(Dynamic Shunt Cell Transmission Model,DSCTM),基本原理如图1所示。图中,正方形方框代表元胞,路段划分的元胞数由式(2)决定。信号控制“十”字交叉口处,东西直行及右转交通流处于绿灯相位,故δ3,4(k)=δ3,10(k)=1,南北直行及左转交通流处于红灯相位,故δ9,4(k)=δ9,10(k)=0。

图1 DSCTM基本原理Fig.1 Basic schematic diagram of DSCTM
结合交通流迟滞现象与元胞流量传递过程,引入元胞状态因子φl(k),实时判断元胞内交通流状态。当元胞处于自由流状态时,φl(k)=0;当元胞处于拥堵流状态时,φl(k)=1;当元胞处于亚稳态,将保持上一时刻交通流状态,φl(k)取值不变。采用具有普适性的路段元胞划分方法,路段元胞个数满足条件为
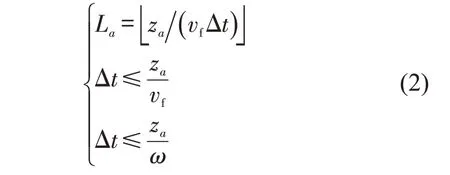
式中:La为路段a划分的元胞数量;za为路段a长度;Δt为时间步长。按此划分方法,元胞实际长度与基本长度z0(z0=vfΔt)相差很小,可近似运用z0计算元胞间传递的车辆数。
城市道路交叉口处会涉及元胞的分流与合流。为描述分流与合流场景,令LUP,l表示元胞l的上游元胞集合,LDOWN,l表示元胞l的下游元胞集合;引入分流参数βl,j表示从元胞l传输至元胞j的流量占元胞l总输出流量的比例,满足βl,j∈( 0,1),βl,j=1,βl,j的具体数值由路径流量分布状态确定。考虑城市道路交叉口信号控制对交通流的影响,引入信号控制因子δl,j(k)指示交叉口交通流的通行权,若δl,j(k)=1 表示从元胞l到元胞j具有通行权(处于绿灯相位);反之,若δl,j(k)=0 表示从元胞l到元胞j无通行权(处于红灯相位)。对于无信号控制交叉口,令δl,j(k)≡1。
1.2 算法设计
地震、暴雨及恐怖袭击等重大扰动事件对路网造成的影响通常持续数天甚至数周的时间。由于出行者具有学习能力,会根据获取的路网信息及历史经验动态调整出行行为,使交通需求在不同路径上的分布随时间(通常以天为单位)动态变化。
基于上述分析,本文将研究时域设定为以天为单位的一段时间长度,假定路径流量以天为单位动态更新,同时,以若干时段流量分布表示当天流量分布状态。令D={1 ,…,d,…} 为研究时域集合,Γd={1 ,…,τ,…} 为第d天的研究时段集合。考虑一个强连通城市道路网络G=(N,A) ,其中,N为网络节点集合,A为路段集合。令W为OD 对集合,Rw为OD对w∈W之间的路径集合,为第d天τ时 段OD 对w间 路 径r上 的 流 量;令L={1 ,…,l,…} 为路网元胞集合;令K={1 ,…,k,…}为时间步集合。
DSCTM算法实现步骤如下。
Step 1 初始化。确定OD对集合W,路径集合Rw,元胞集合L等路网结构参数,以及研究时域集合D,研究时段集合Γd,时间步集合K,时间步间隔Δt等仿真参数。
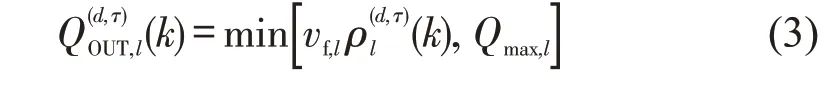
式中:vf,l为元胞l的自由流速度;(k)为第d天τ时段k时间步元胞l交通流密度;Qmax,l为元胞l饱和流率。
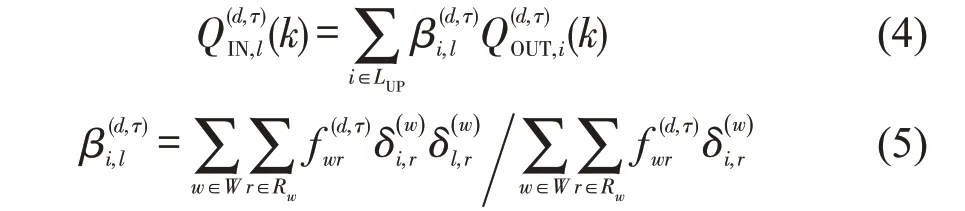
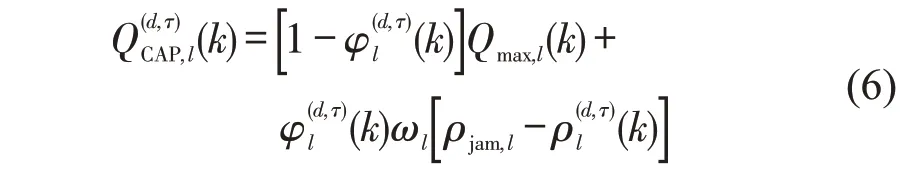

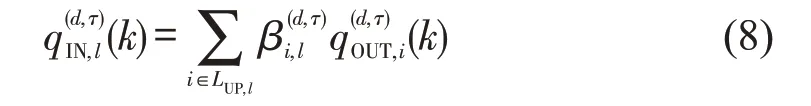
Step 7 更新元胞的交通流密度。
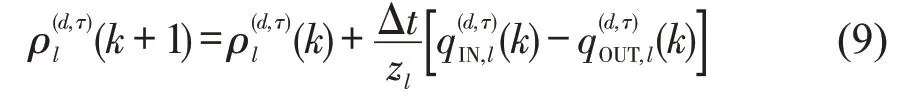

2 路径流量动态更新模型
如式(5)所示,要获得交叉口处第d天τ时段的分流系数,必须先确定第d天τ时段路径流量分布状态。由于重大扰动事件很可能造成路网性能退化,加之出行者具有趋利避害的本能和学习能力,在事件影响期间,出行者可能根据获取的路网信息并结合历史经验不断更新路径选择,造成路径流量逐日变化。由于行程时间是出行者选择路径时首要考虑的因素,因此,本文以路径行程时间作为出行者选择路径的基本依据。同时,由于获取信息的完备性不足,出行者无法确知每条路径的实际行程时间,只能依据理解或估计的行程时间选择路径。此外,在无法获得准确行程时间的背景下,出行者通常会综合历史经验计算期望理解行程时间。基于上述分析,本文以理解路径行程时间作为择路依据,明确考虑历史经验对决策行为的影响,使用加权平均学习算子模型[16]计算路径期望理解行程时间,使用Logit模型计算路径选择概率,获得当前时段路径流量分布状态。路径流量动态更新的详细步骤如下。

式中:|K|为时间步总数。

式中:λ∈( 0,1) 为权重系数;M为记忆容量,反映影响当前时段出行决策的历史信息时限。由式(13)可知,距离当前时段越接近的历史信息对当前时段期望路径行程时间的影响越显著。

式中:ε为理解时间误差,假定其服从均值为0 的Gumbel分布。

式中:θ >0 为离差系数,与出行者对出行时间的估计误差成反比,即θ值越大,估计误差越小。
Step 5 计算当前时段路径流量。
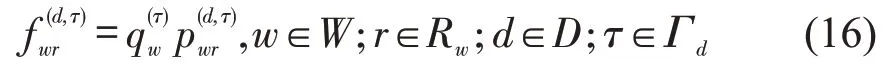
3 路网韧性评估
如前所述,韧性的核心内涵是反映路网抵御扰动和从扰动中快速恢复的能力。韧性测度指标必须体现韧性核心内涵。扰动事件影响期内的路网性能演化过程如图2所示。图2中,d0,de,ddeg,dr分别为扰动前某特定时间、扰动发生时间、路网性能退化到最低程度时间以及路网性能恢复到预期状态时间;F(·)为路网基础性能指标函数。
参考文献[9],通过扰动事件影响期内路网基础性能指标的动态累积变化评估韧性,但基础性能指标的选取与文献[9]不同。文献[9]以网络最大流作为路网基础性能指标,未能体现出行决策行为对流量分布的影响。基于此,本文选用路网效率[17]作为基础性能指标。路网效率以路网流量分布状态为基础,可以反映路网平均个体出行成本代价,间接体现了路网服务水平高低程度,即路网效率越高,平均个体出行成本代价越小,路网服务水平越高。令F(d)为第d天的路网效率,根据文献[17]计算,即

令ϕ(d)为第d天的路网韧性,计算式为
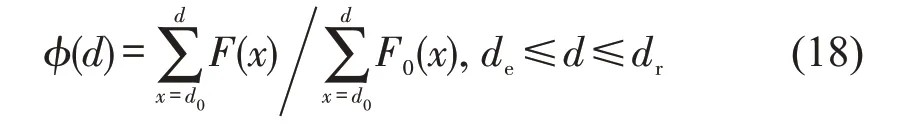
式中:F0(x)为正常条件下第x天的路网效率。式(18)中,分子表示从扰动事件发生到第d天路网的累积性能;分母表示正常条件下(不发生扰动事件)同时间长度路网的累积性能。如图2所示,ϕ(d)可表示为斜线区域面积S1 与阴影区域(包含斜线区域)面积S2的比值。
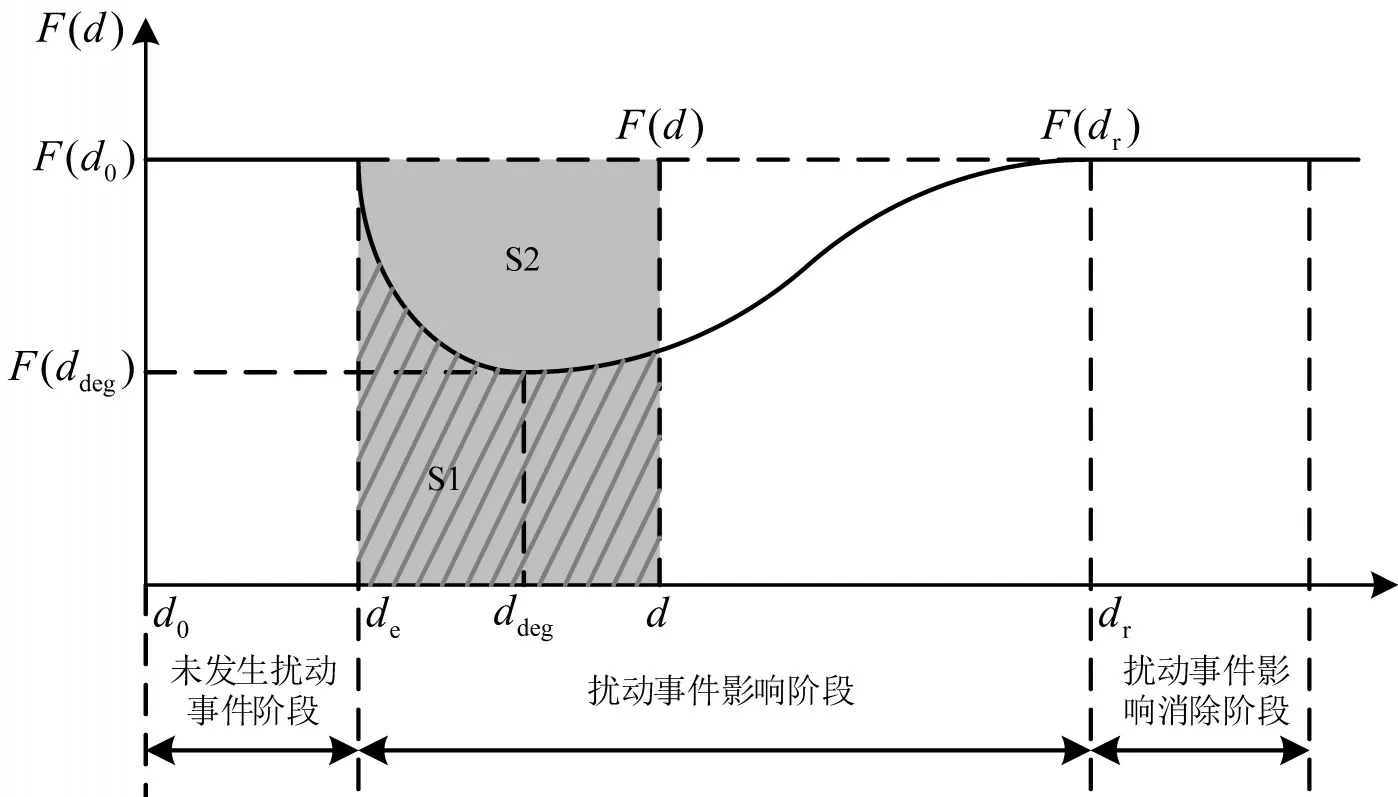
图2 扰动事件下路网状态演化过程Fig.2 Road network state evolution under disturbance events
4 算例分析
采用广泛使用的Sioux Falls网络为测试网络,网络包括4 个OD 对和76 条路段。4 个OD 对分别为1-18,1-20,2-18,2-20。图3中,路段上数字表示路段编号,O为起始节点,D为终端节点,信号灯为东西和南北两相位设置,每相位绿灯时间均为60 s,信号灯周期时长为120 s。若无特殊说明其他参数设置如下:vf=50 km·h-1,ω=21.4 km·h-1,Δt=10 s,ρjam=120 veh·h-1,Qmax=1800 veh·h-1,| |K=1080 ,λ=0.8,M=5,θ=0.12。
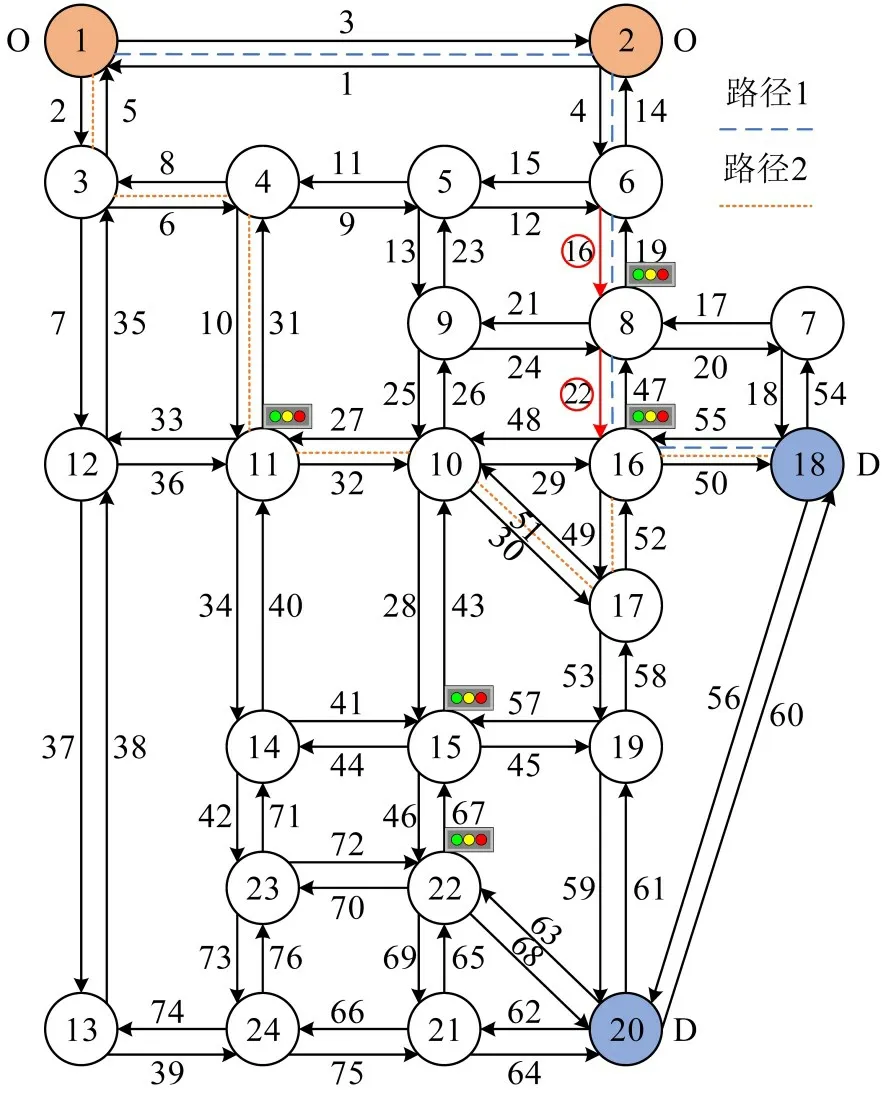
图3 Sioux Falls路网结构Fig.3 Sioux Falls network structure diagram
仿真场景为:仿真30 d 内路网流量变化情况,每天研究3个时段,其中,时段1和时段3为平峰时段,时段2 为高峰时段。3 个时段4 组OD 对的假定第10 天受强暴雨袭击造成路段16 和路段22通行能力下降50%,路段受损后立即维修,第20天修复完成。假定扰动发生在第10 天高峰期时段后,即扰动事件仅对第10 天以后的出行决策行为产生影响。路段长度及路段元胞划分如表1所示。
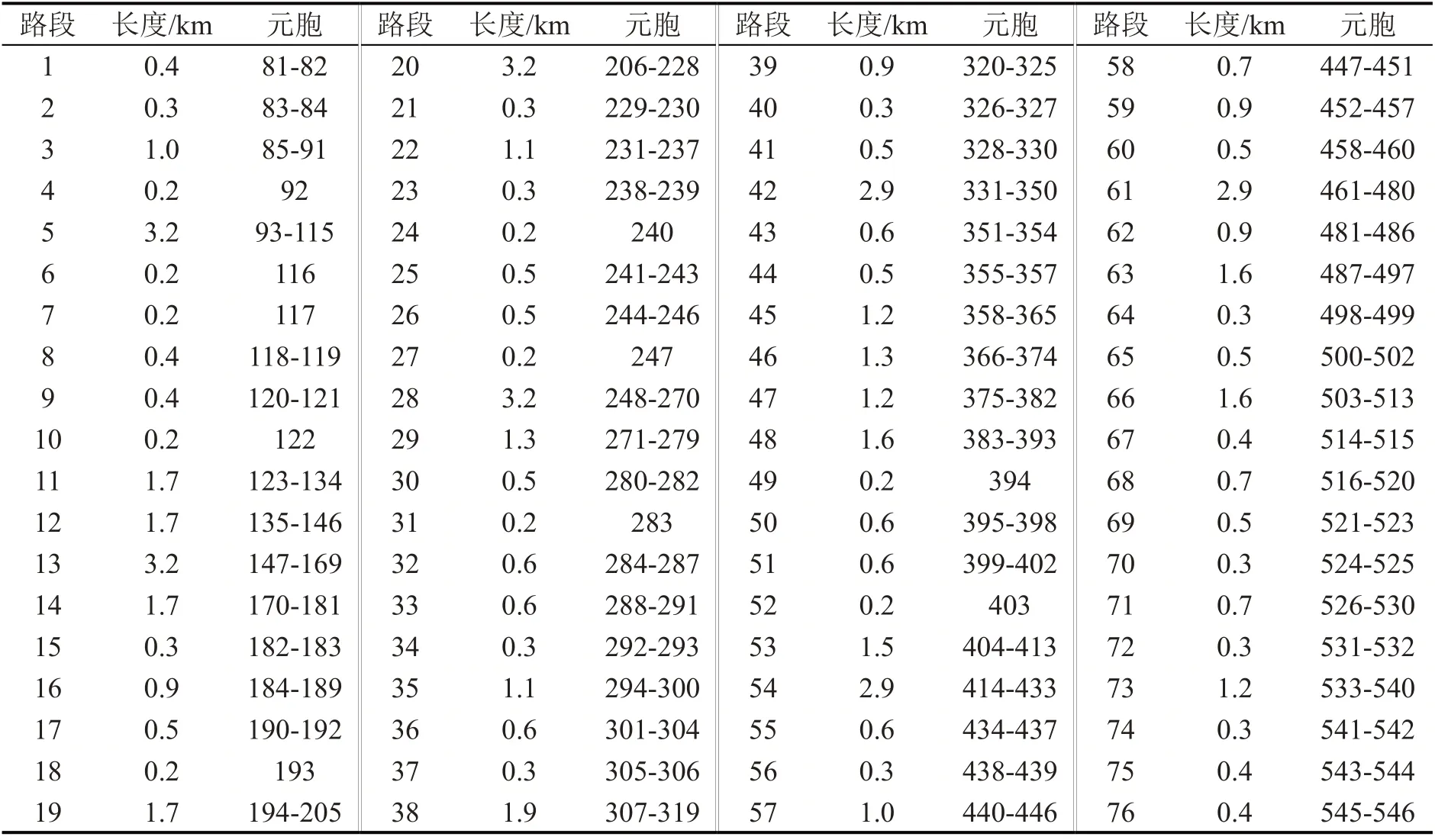
表1 路段-元胞关系表Table 1 Link-cell relationship
图4~图6 描述了研究时域内路网交通流密度变化情况。由图4 和图5 可知,扰动事件对平峰时段路网交通流密度的影响并不显著,但对高峰时段(时段2)交通流密度影响较大。需求流率(veh·h-1)分别为:=300,=555,=360;=200,=370,=240;=300,=555,=360;=250,=462,=300。

图5 第2天和第12天交通流密度Fig.5 Traffic flow density on days 2 and 12
由图4 可知,从第11 天~第20 天,高峰时段(时段2)路网交通流密度较扰动发生前显著提高,出现明显的“峰值区域”。此外,扰动事件造成每日路网平均交通流密度显著提高。如图6 所示,第10天路网平均交通流密度为7.34 veh·km-1,而受扰动事件影响,第11 天路网平均交通流密度上升至9.08 veh·km-1,增长了23.71%,之后出现震荡,直至第20 天受损路段修复完成后,路网平均交通流密度稳步下降,在第22天时达到稳定状态。

图4 路网交通流密度Fig.4 Traffic flow density

图6 路网平均交通流密度Fig.6 Average traffic flow density
图7 从微观尺度描述了研究时域内受损路段元胞交通流密度动态变化情况。由图7 可知,在扰动事件影响期内,位于路段16 的元胞187,188,189 交通流密度出现明显提升,其中,元胞189 的波动最为显著。原因在于,元胞189 位于临近信号控制交叉口的上游,受信号控制频繁出现排队现象,加之元胞189 位于通行能力退化的受损路段,受元胞输出能力显著下降与信号控制叠加影响,在扰动事件影响期内元胞189 交通流密度持续处于高位。

图7 受损路段元胞交通流密度Fig.7 Traffic flow density of the damaged cell
图8展示了研究时域内部分路径交通流率动态变化情况。由图8可知,发生扰动事件后,路径1(路段序列为:3→4→16→22→50)的流率从31 veh·h-1附近下降至27 veh·h-1附近,路径2(路段序列为:2→6→10→32→30→52→50)的流率从32 veh·h-1附近增加至34 veh·h-1附近。出现路径流率此消彼长的原因在于,路径1 包含受损路段16,扰动事件发生后,出行者会根据路段受损情况调整出行决策行为,导致选择路径1的出行者比例下降;同时,由于路径1与路径2同属一个OD对,路径2可作为路径1的替代路径,因此,选择路径2的出行者比例上升,路径2的流率增加。

图8 扰动事件影响下的路径流率Fig.8 Path flow rate under influence of disturbance event
图9 描述了研究时域内路网效率变化情况以及扰动事件发生后的路网韧性变化情况。由图9可知,扰动事件发生后,由于路网供给条件的明显变化,导致出行者可能频繁调整出行路径以规避不利影响,因而,导致一段时间内路径流率分布处于“无序”状态,这种“无序”导致路网效率明显下降。例如,路网效率在第10 天时为0.234,而第11 天时下降至0.211,下降了9.83%,直到第14天恢复至新的稳定状态,第20天受损路段修复后,路网效率逐步恢复至扰动前的水平。同时,由图9 可知,本文构建的基于路网效率的韧性指标可以全面反映扰动事件发生后,路网性能退化到逐步恢复全过程的动态累积性能,直观展示路网抵御扰动并从扰动中恢复的能力,契合韧性的内涵。例如,第11天时路网韧性为0.902,表示扰动事件的发生导致路网效率下降至正常情景时的90.20%,第20 天时路网韧性为0.968,表示扰动事件发生后的10 天(从第11天~第20天)内,累积路网效率为正常情景下的96.80%。
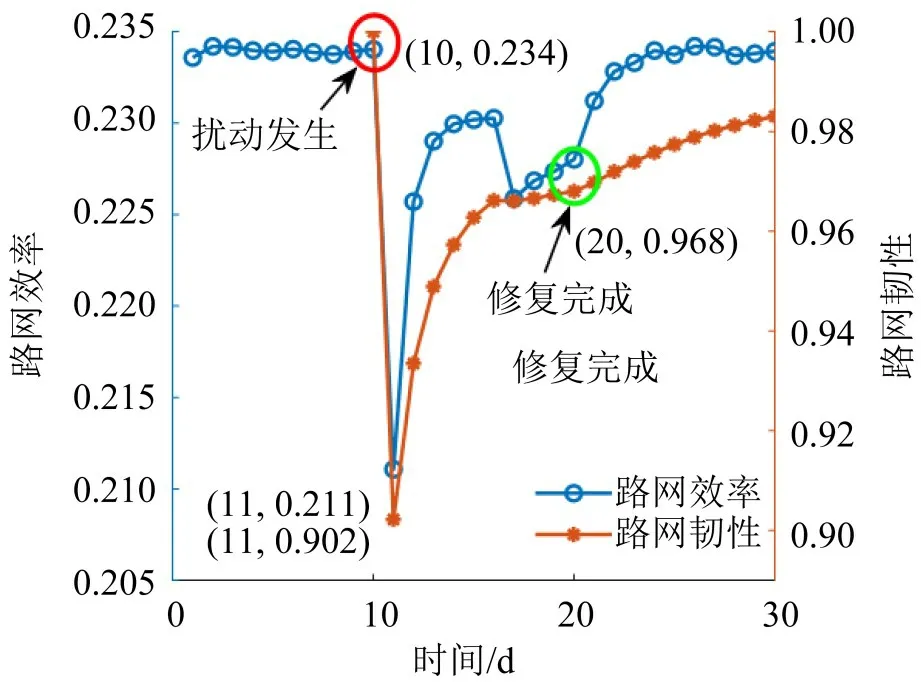
图9 路网效率与路网韧性Fig.9 Efficiency and resilience of road network
使用本文提出的DSCTM 与传统CTM 获得的路网性能指标差异如图10和图11所示。

图10 不同元胞传输模型对路网效率的影响Fig.10 Effects of different CTMs on network efficiency
由图10和图11可以明显看出,不同CTM获得的路网性能指标存在明显差异。从路网效率看,扰动事件影响期内,使用传统CTM 获得的路网效率保持稳定,无明显波动起伏,而使用DSCTM 获得的路网效率具有明显的波动起伏过程。路网效率的显著差异直接导致路网韧性的明显不同。出现这种明显差异的根本原因在于,传统CTM 不考虑出行决策行为影响,将分流系数设置为常数,意味着扰动事件影响下出行者的流率分布保持稳定不变,而DSCTM 明确考虑了出行决策行为变化导致的路径流率变化,将分流系数设置为路径流率分布的函数,建立出行决策行为与元胞流量传输的动态耦合关系,可准确反映路径流量变化与交叉口元胞分流比例的自洽机制。显然,在实际交通场景中,由于出行者的主观能动性,重大扰动事件下出行者很可能会根据路网条件对路径选择做出适应性调整。因此,本文提出的DSCTM模型更符合实际。

图11 不同元胞传输模型对路网韧性的影响Fig.11 Effects of different CTMs on network resilience
参数λ,M,θ取值变化对路网韧性的影响如图12~图14所示。

图12 参数λ 对路网韧性的灵敏度分析Fig.12 Sensitivity analysis of parameters λ to network resilience
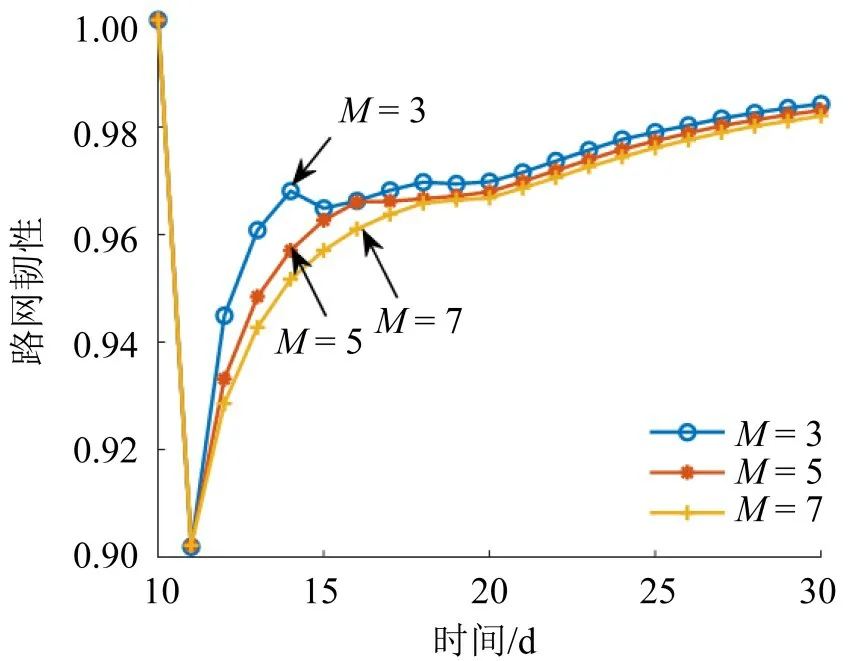
图13 参数M 对路网韧性的灵敏度分析Fig.13 Sensitivity analysis of parameters M to network resilience
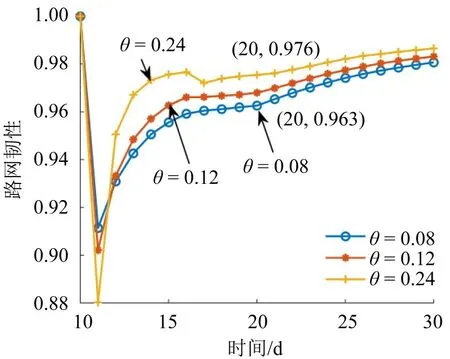
图14 参数θ 对路网韧性的灵敏度分析Fig.14 Sensitivity analysis of parameters θ to network resilience
由图12~图14可知,参数λ,M,θ取值变化均会对路网韧性产生影响。其中,参数λ,M取值变化对路网韧性的影响相对较小,但参数θ取值变化对路网韧性的影响十分显著。从图12 可以看出,当参数λ分别为0.6,0.8,0.9时,路网韧性指标曲线分化不显著,取值比较接近;同样,从图13 可以看出,当参数M分别为3,5,7 时,路网韧性指标也比较接近。然而,从图14可以看出,当参数θ分别为0.08,0.12,0.24 时,路网韧性指标曲线出现明显分化和显著不同。例如,当θ=0.08,第20 天时路网韧性指标为0.963,而当θ=0.24,第20 天时路网韧性指标变化为0.976。由于参数λ,M取值反映了出行者的行为特征,θ取值反映了出行者估计误差的大小,间接反映了出行者获取信息的质量,即θ取值越大,出行者估计误差越小,获取的信息质量越高。参数λ,M,θ从不同侧面反映了出行者的行为特征。综合图12~图14的结果可以看出,出行者的行为特征对路网韧性会产生不同程度影响,因此,在韧性评估中忽视出行决策行为潜在影响将获得次优甚至明显偏离实际的结果。
5 结论
(1)提出的动态分流元胞传输模型明确考虑了重大扰动事件下由于路网供给条件的显著变化可能导致的出行者决策行为适应性调整,通过设置交叉口动态分流参数,建立出行决策行为与元胞流量传输的动态耦合关系,准确反映路径流量变化与交叉口元胞分流比例的自洽机制。相比于传统元胞传输模型,可以准确描述重大扰动事件下路网交通流动态特性,获得更加准确的交通流特性参数。
(2)构建的基于路网效率的韧性指标可以反映扰动事件发生后路网性能退化到逐步恢复全过程的动态累积性能,直观展示路网抵御扰动并从扰动中恢复的能力,契合韧性内涵。
(3)参数λ,M,θ取值变化会对路网韧性产生不同程度影响。其中,参数λ,M的影响相对较小,但参数θ的影响十分显著。由于参数λ,M,θ从不同侧面反映了出行者的行为特征,因此,表明韧性评估中若忽视出行决策行为潜在影响将获得次优甚至明显偏离实际的方案或结果。

