考虑对地航速和航向的船舶典型轨迹提取方法

刘畅，张仕泽，李倍莹，李波

(1.大连海事大学，a.信息科学技术学院，b.航海学院，辽宁 大连 116026；2.辽宁工业大学，电子与信息工程学院，辽宁 锦州 121001)

0 引言

船舶自动识别系统是一种新型获取船舶信息的重要手段，AIS信息蕴含着海上大量的船舶运动特性[1]。在海上交通应用中，聚类结果可以得到惯用的行驶路线和交通量分布。船舶轨迹聚类作为常用的数据挖掘方法，将不同船舶的轨迹数据整合到各个聚类集群中[2]。国内外学者对船舶AIS聚类进行了一系列研究，将聚类方法分成3类。

第1类是以整条船舶的AIS轨迹作为一个聚类单元进行聚类。牟军敏等[3]改进传统的Hausdorff距离，利用船舶轨迹的距离均值代替尺度参数，以船舶的整条轨迹作为聚类对象，获得了长江口水域的聚类结果。ZHAO 等[4]利用DP 算法压缩船舶轨迹，以压缩过程中的形状稳定性确定DP 算法的阈值，通过DBSCAN(Density-Based Spatial Clustering of Applications with Noise)算法提取海上交通特征，再根据船舶AIS 数据集的统计特征确定DBSCAN算法的参数。YANG等[5]提出了一种基于密度的轨迹聚类(Density Based Trajectory Clustering of Applications with Noise, DBTCAN)，该算法可以携带噪声，并利用KANN(K-Average Nearest Neighbor)方法确定DBTCAN算法的参数。ZHANG等[6]将改进的SSPD(Symmetrized Segment-Path Short)距离作为轨迹的相似性度量，解决了SSPD 距离无法识别轨迹方向和轨迹端点不一致的问题。利用船舶的整条轨迹进行聚类，虽然能更好地挖掘轨迹的关键路径，但会丢失一些相似的子轨迹段，缺少局部区域的重要信息。

第2类是以船舶的子轨迹进行聚类。首先，对船舶轨迹进行分段，然后，对分段后的子轨迹进行聚类。江玉玲等[7]将对地航速和对地航向作为划分船舶轨迹的信息度量，利用DBSCAN 算法对轨迹段进行聚类。GAO 等[8]将整条船舶的AIS 轨迹分割成子轨迹，通过7组编码的方式定义这些子轨迹段，利用T-SNE(T-distributed Stochastic Neighbor Embedding)算法降低数据维度，再通过谱聚类算法聚类船舶子轨迹段。LI 等[9]考虑了Hausdorff 距离在计算船舶轨迹间距时容易受到轨迹点跨度大和轨迹点缺失等问题的影响，改进Hausdorff距离，利用改进的DBSCAN 算法聚类轨迹段，再通过质心向量提取方法得到了虚拟的典型航迹。对分段后的子轨迹进行聚类，虽然有不丢失局部特征和不丢失轨迹趋势的优点，但不同的划分准则导致截然不同的聚类结果，且算法运行时间过长。

第3类是对单个轨迹点的数据进行聚类，主要基于纬度和经度。李倍莹等[10]将统计学知识引入到聚类算法中，根据均方根误差的变化趋势自适应地选择K 质心聚类的输入参数。LIU 等[11]在DBSCAN 聚类阶段考虑了对地航速和对地航向非空间属性，使位置相近、航速和航向相似的轨迹点可以组合成一个集群。XU等[12]利用船舶轨迹点的位置、航速和航向划分复杂水域，并结合这3 个属性扩展原有的DBSCAN 算法，并利用矢量点表示的思想提出典型轨迹的提取方法。对船舶的轨迹点进行聚类是最常用的方法，主要是基于轨迹点的经度和纬度，然而，基于轨迹点的聚类忽略了同一轨迹相邻点之间的时空相关性。

通过对上述文献的分析，本文在3个方面进行了主要研究。首先，在轨迹压缩方面，大多数的轨迹压缩算法都是基于DP算法进行的，但传统的DP算法只考虑了轨迹的位置，没有考虑船舶的对地航速和航向，本文利用改进的DP算法压缩轨迹，充分考虑了船舶轨迹的多维信息。其次，在轨迹聚类方面，利用DBSCAN 聚类虽然能够聚类任意形状的稠密数据，但如果样本的密度相差较大，聚类质量就会相对较差；K质心聚类是一种简单快速的聚类算法，但它对初始质心敏感，不适用于非凸数据集，不同初始质心得到的结果完全不同，且对噪声敏感。与以上聚类算法相比，谱聚类算法对初始输入数据不敏感，具有识别非凸数据的能力，且时间复杂度低，并针对轨迹点聚类忽视了时空相关性和运动趋势的问题，提出多属性轨迹相似性度量方法。再次，考虑到输入参数对聚类质量的影响，引入Calinski-Harabasz 指标评估聚类算法，自适应地选出最优初始参数。

1 船舶轨迹点数据预处理

AIS提供船舶静态和动态的实时信息(例如，经度、纬度、航速及航向等)。经过解码的数据需要清洗才能运用，由于删除异常点和重复点会导致轨迹点不连续，需要重建船舶轨迹[13]。考虑低数据频率的曲线轨迹处理问题，选择三次样条插值法修复船舶轨迹。经过修复后的轨迹数据由于算法的开销较大，不能直接作为聚类算法的样本，因此，需要压缩船舶轨迹。

DP 算法由Douglas 和Peucker 于1973 年首次提出，该算法可以递归地分割线数据，并通过阈值控制压缩质量，常用于简化运动物体的轨迹[14]。DP算法思路是：假设P1-P2-P3-P4-P5-P6-P7-P8为船舶航行轨迹的位置点图，第1 步，把清洗后的船舶起始点连线，计算所有中间航迹点到这条直线的距离，依次比较这些距离，得到最大距离dmax。第2步，把距离最大值dmax和初始阈值dth比较，若dmax＞dth，则把中间点全部舍去；若dmax≤dth，则把这条曲线分成两部分。第3步，对这两部分轨迹分别执行上述操作，依次迭代，直到压缩完成P1-P4-P6-P7-P8，如图1所示。

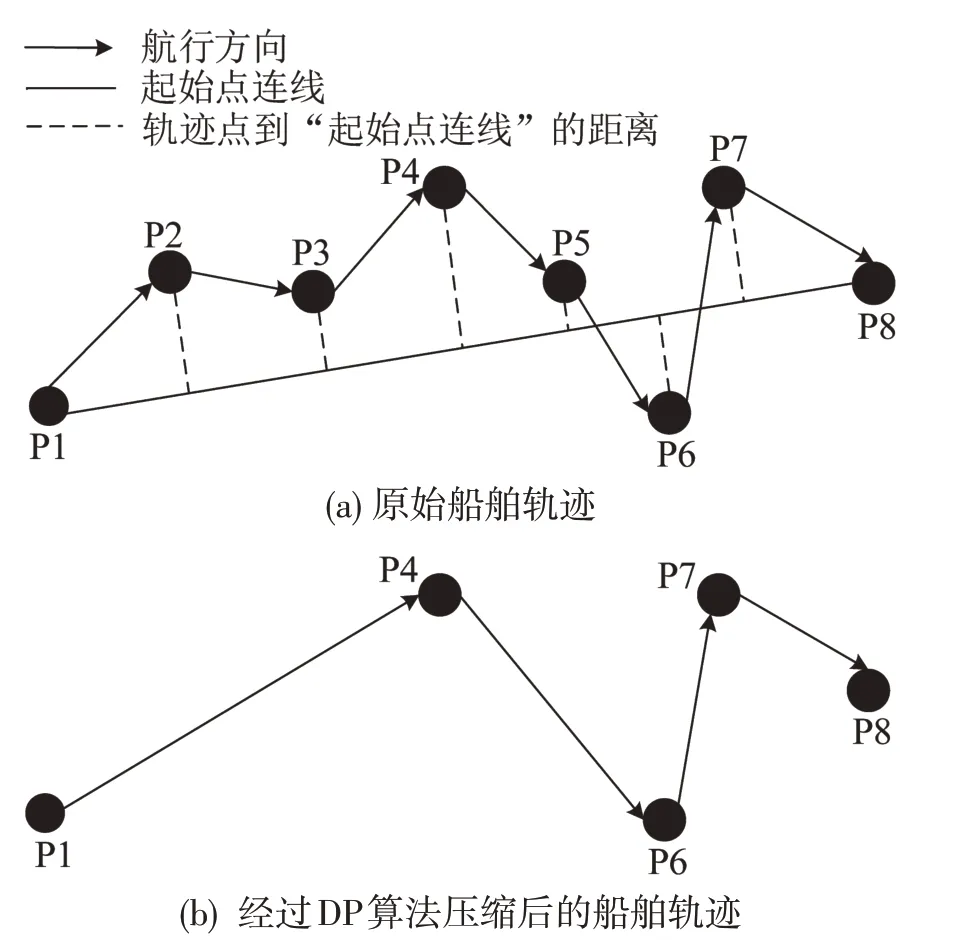
图1 DP算法轨迹划分示意Fig.1 DP algorithm trajectory partition diagram

DP 算法是根据点到轨迹段的距离进行划分的，在压缩轨迹的同时保存了轨迹的形状特征。但是当处理移动对象时，传统DP 算法的缺点是没有考虑船舶其他重要维度。因此，本文改进传统的DP算法，把航速和航向加入到DP算法的压缩过程中，改进的DP算法流程如图2所示。

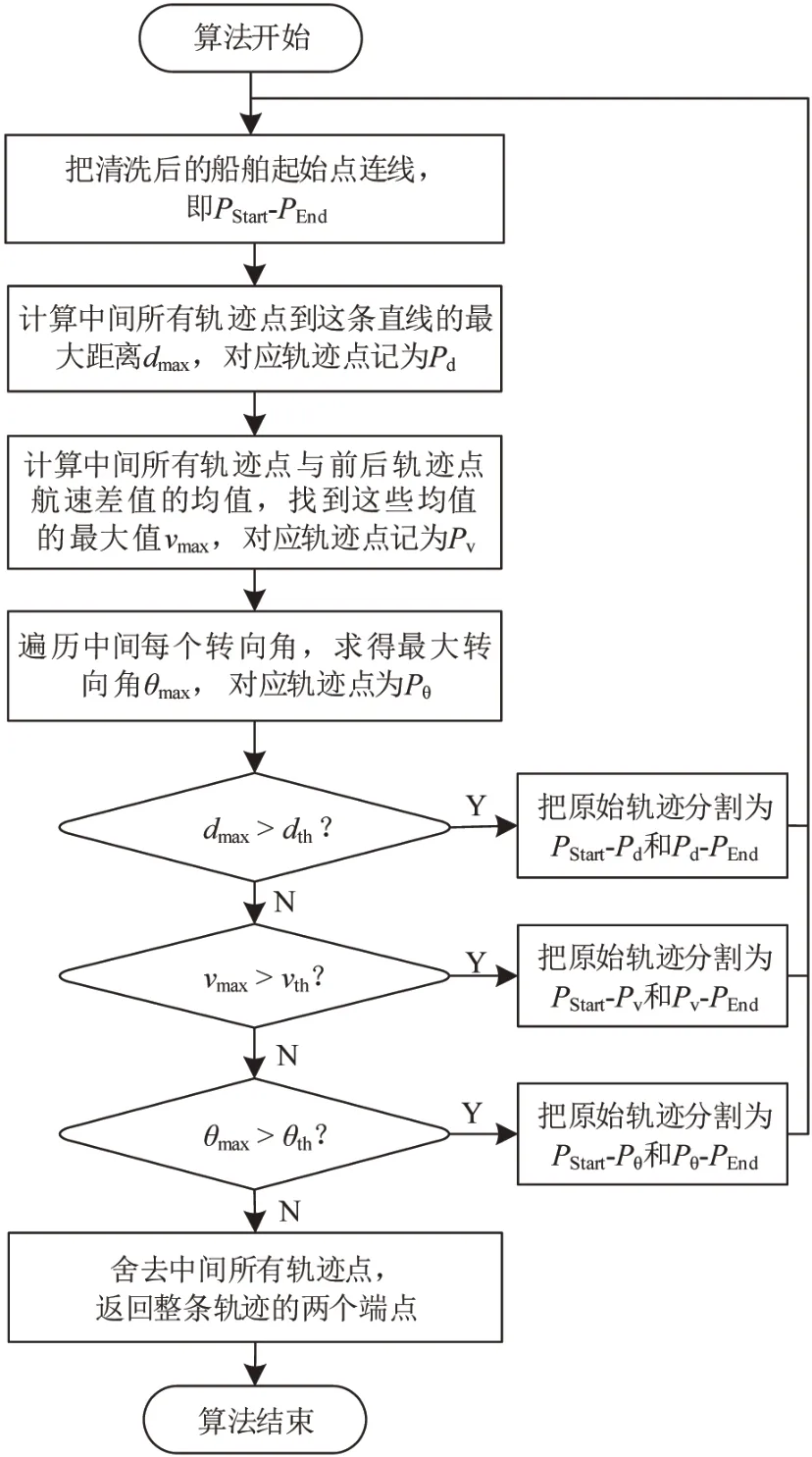
图2 改进DP算法流程Fig.2 Improved DP algorithm flow chart

2 改进谱聚类对船舶典型轨迹的提取方法

将原始船舶轨迹经过数据清洗、数据修复和数据压缩后，再作为聚类算法的输入样本。引入Calinski-Harabaz指标评价不同参数的谱聚类算法，选择Calinski-Harabaz 指标得分最高的输入参数。计算每类集群的中心点，把点集成线，并可视化展示，算法流程图如图3所示。

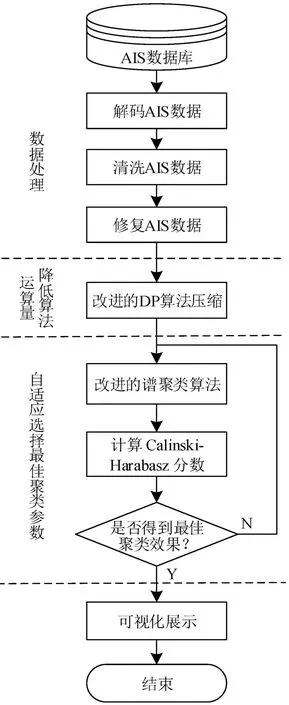
图3 算法流程Fig.3 Agorithm flow chart

2.1 船舶轨迹的相似性度量

在聚类过程中，需要一个距离矩阵来度量船舶轨迹之间的相似度。轨迹相似性的度量方法有多种，例如，欧氏距离、DTW(Dynamic Time Warping)距离、SSPD 距离、Fréchet 距离和Hausdorff 距离。常用的轨迹相似性度量方法是DTW 距离和Hausdorff 距离，DTW 距离是一种计算两个不同长度时间序列之间距离的方法，该方法考虑的是船舶轨迹在特定时间和特定环境中的运动路径，而不是按照时间排序的数据点集合，且未考虑船舶轨迹和其他重要维度；Hausdroff距离是另一种常用的轨迹相似性度量方法，该方法的缺点是对噪声敏感[14]。

针对轨迹点聚类忽视时空相关性和运动趋势的问题，建立多属性相似性度量方法，其中，xi和yi为船舶轨迹点i的经度和纬度；i和j为轨迹点编号；de(i,j)为两个轨迹点之间的位置距离，即

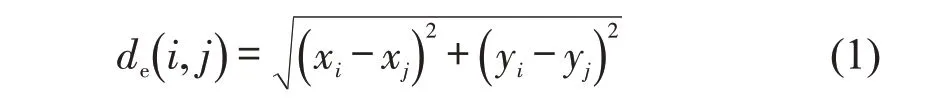
vi为当前轨迹点i的航速；dv(i,j)是对船舶轨迹之间的航速进行比较，即

hi为当前轨迹点i的航向；dh(i,j)是对船舶轨迹之间的航向进行比较，即

将各个属性的度量距离除以各自距离矩阵中的最大值，得到归一化后的位置距离dnorme(i,j)、航速距离dnormv(i,j)和航向距离dnormh(i,j)。定义位置属性的权值we、航速属性的权值wv和航向属性的权值wh，将各个度量距离乘以各自的权值并求和，得到了包含船舶多属性的距离。利用多属性相似性度量方法更准确地定义了船舶的时空行为，具体为

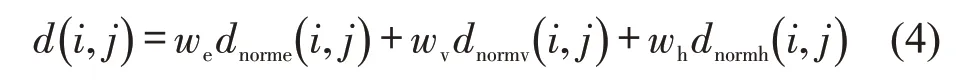
2.2 基于船舶轨迹的谱聚类算法

谱聚类(Spectral Clustering, SC)是一种根据图形划分的聚类算法。把聚类样本看成空间中的点，将数据点用边连接起来，相距较近的数据点权重值较高；相反，相距较远的数据点权重值较低[15]。船舶轨迹点P1-P2-P3-P4-P5-P6-P7-P8-P9的谱聚类切图如图4所示。

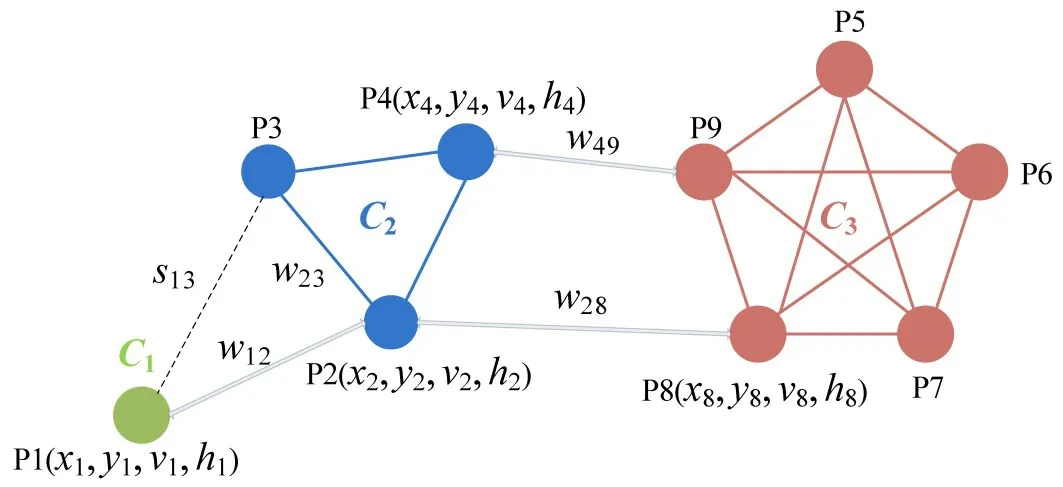
图4 基于船舶轨迹的谱聚类切图Fig.4 Spectral clustering cut graph based on ship trajectory

每个轨迹点都携带了当前轨迹的位置信息(xi,yi)、航速信息vi和航向信息hi。具体聚类过程如下。

Step 1 利用提出的多属性相似性度量方法计算每两个轨迹点的距离，计算得到的度量距离s(i,j)与规定的距离阈值sth进行比较，若s(i,j)＜sth，则保留度量距离s(i,j)；若s(i,j)≥sth，则认为此两个轨迹点距离无穷远。图4中，轨迹点P1和轨迹点P3 的度量距离s(1,3)大于距离阈值sth，即认为轨迹点P1 和轨迹点P3 相似性为零，图4 中用虚线连接这两个轨迹点。利用全连接法对所有轨迹点进行相似性度量，最终得到了多属性距离矩阵Sn×n，其中，n为数据集中轨迹点的个数。

Step 2 利用高斯径向核函数作为邻接矩阵Wn×n的度量，其中，σ为尺度参数，wij为轨迹点i和轨迹点j的相似度，wij定义为

Step 3 图4 中，若两个轨迹点的相似度不为0，则用实线相连；相反，没有相连的两个轨迹点代表着相似度为0。计算邻接矩阵Wn×n每行元素之和，组成对角矩阵Dn×n,dij定义为

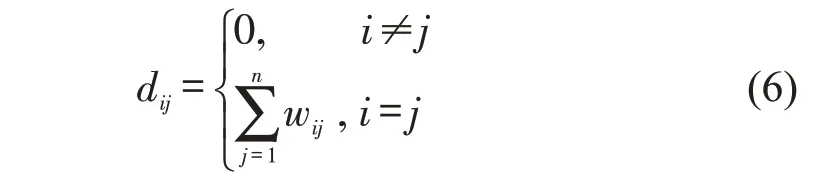
Step 4 定义拉普拉斯矩阵Ln×n=Dn×n-Wn×n，lij定义为

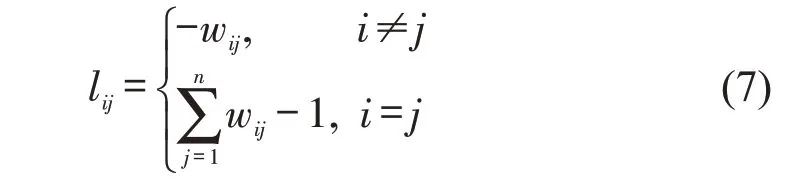
Step 5 拉普拉斯矩阵Ln×n是对称且半正定矩阵，定义标准化的拉普拉斯矩阵Lsym为

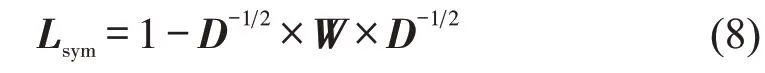
Step 6 计算标准化的拉普拉斯矩阵Lsym依次递增的前k个特征值λ1,λ2,λ3,…,λk，k值代表着分类集群的数目，再计算这些特征值所对应的特征向 量α1,α2,α3,…,αk，将 这 些 特 征 向 量α1,α2,α3,…,αk组成一个新的矩阵An×k，即

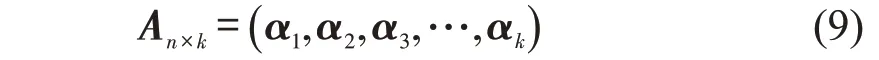
Step 7 定义γq(q=1,2,…,n)是 矩 阵An×k的第q行向量，再利用K-Means 聚类将γ1,γ2,…,γq(q=1,2,…,n)聚类成簇C1,C2,…,Ck。不同k值的选择影响着最终的聚类质量，在图4 的数据集中，当k=3 时得到了3组分类集群C1,C2,C3。

2.3 聚类性能评价指标

由于分类簇数目的选择影响着最终的聚类效果，因此，为了自适应地确定最佳聚类参数，引入Calinski-Harabaz 指 标 评 估 聚 类 算 法[15]，Calinski-Harabaz指标是一种常用的内部评价指标，Calinski-Harabaz 为分散度和紧密度的比值。Calinski-Harabaz指标的计算式为

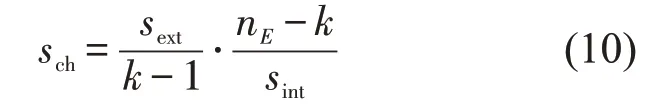
式中：k为簇的个数；nE为整体数据集E的数据个数；sint为集群内元素距离差值矩阵的迹；sext为不同集群之间距离差值矩阵的迹。sext的计算方式为

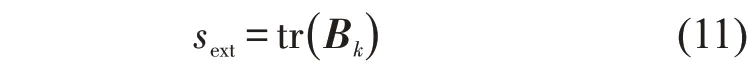
式中：Bk为不同集群之间的距离差值矩阵，计算式为

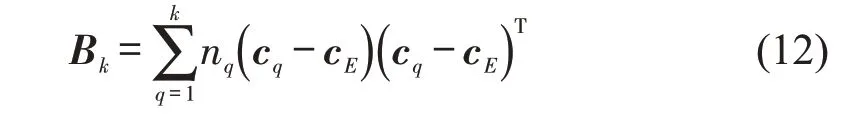
式中：cE为数据集E的中心点坐标向量；cq为集群q的中心点坐标向量；nq为集群q的数据个数。sint的计算式为

式中：Wk为集群内元素的距离差值矩阵；Cq为集群q的点集，计算式为

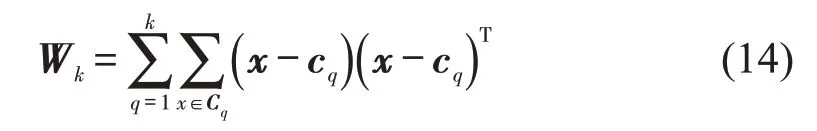
把Calinski-Harabaz 评价方法引入聚类算法中，避免了传统方法选择参数的主观性。根据Calinski-Harabaz指标得分确定最佳的输入参数k，实现参数的自适应选择。

3 实验与验证

3.1 船舶轨迹处理

选取2019年5月1日～3日这2 d内渤海湾水域的AIS数据，WGS84坐标系经度范围117.290039°E～124.23339°E，纬度范围35.995785°N～39.639537°N。在渤海湾水域提取进出山东威海水域的AIS数据；再对此数据进行数据清洗和数据修复；最后对修复后的AIS数据利用改进的DP算法进行压缩。各个算法的船舶数和轨迹点数如表1 所示。山东威海水域船舶轨迹如图5所示。把经过改进DP算法压缩后的船舶轨迹和船舶原始轨迹点集转线，如图6所示。

图5 山东威海水域船舶轨迹Fig.5 Ship track map of Weihai,Shandong

对比图6 可以看出，经改进DP 算法压缩后的船舶轨迹极大程度上保留了原始船舶行程轨迹的各个特征，压缩后的轨迹形状与船舶原始航行轨迹相符。

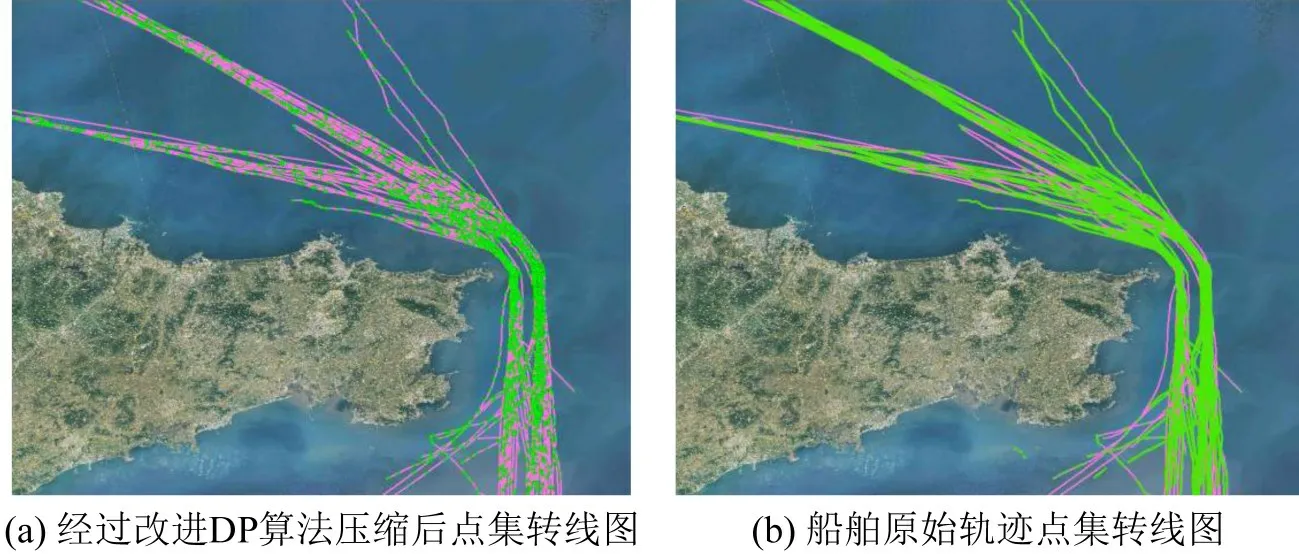
图6 山东威海港部分船舶轨迹Fig.6 Part of ship track at Weihai Port,Shandong

3.2 改进谱聚类算法参数的自适应选择

将进出山东威海港口主航道的AIS 数据运用改进的谱聚类算法进行实验，分别计算了当k取5,6,7,8,9,10,…,30 时 的Calinski-Harabaz 指 标，进出港Calinski-Harabaz 指标随k值的变化趋势如图7所示。

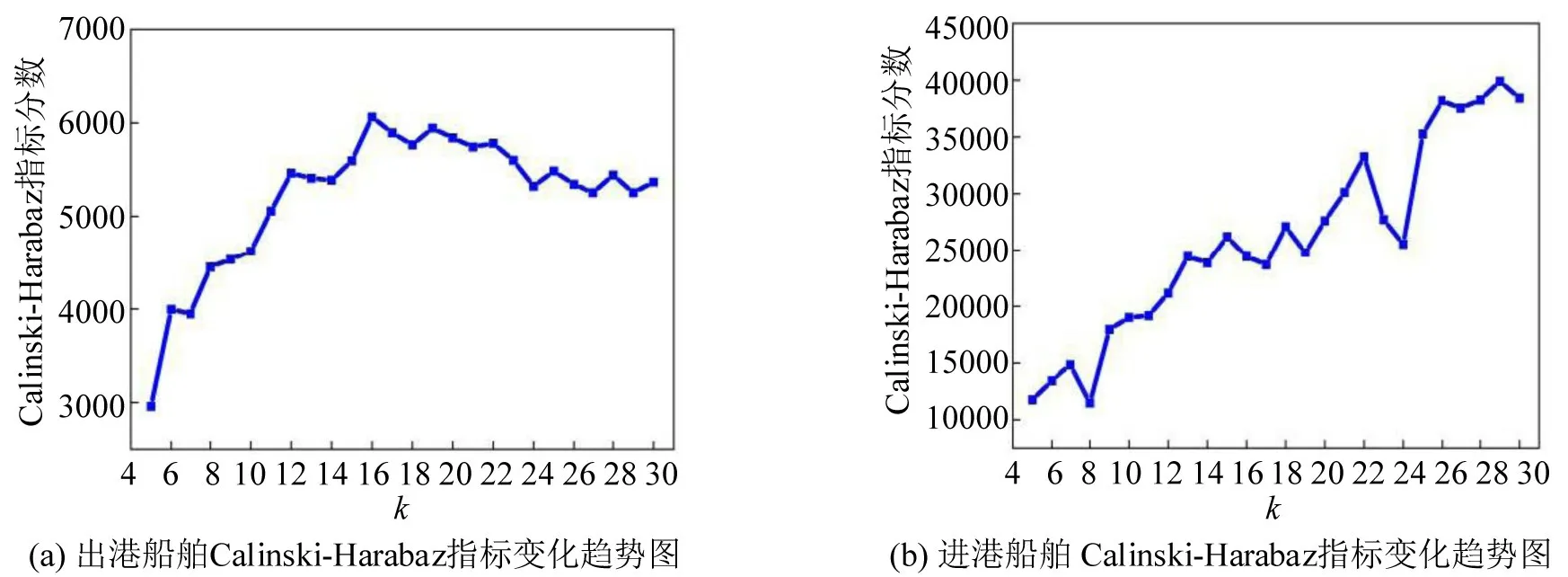
图7 进出港船舶Calinski-Harabaz指标变化趋势Fig.7 Change trend chart of Calinski-Harabaz index of incoming and outgoing ships

Calinski-Harabaz 指标随着k值的上升总体上呈现上升趋势。这是由于随着k值上升，聚类后的轨迹点越能反映原始船舶轨迹的特征，拟合效果也就越好。但k值的增加超过一定的限度会造成过拟合现象，为了用较低k值的聚类结果表示船舶轨迹的真实特征，需要确定唯一的极大值点。出港船舶k值在16左右出现了极大值点，因此，选择k=16作为聚类参数的最佳值。进港船舶分别在22、26和29 左右出现了极大值，k=22、k=26 和k=29 时聚类结果的可视化细节效果如图8所示。

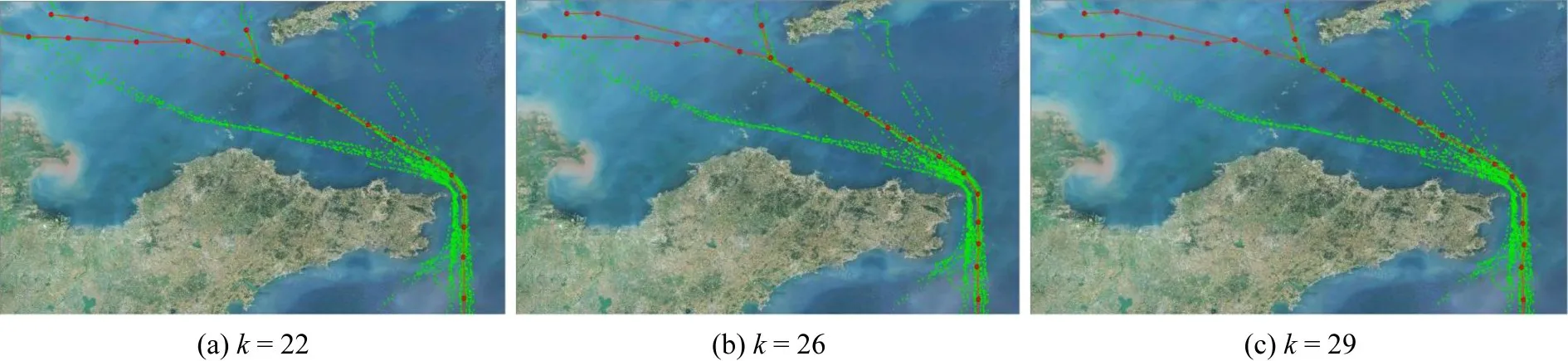
图8 进港船舶部分典型轨迹示意Fig.8 Schematic diagram of typical track of ship entering port

通过图8 的对比可知，输出典型轨迹基本一致，即使在航行复杂的入港区域，也展现出一致的聚类效果，因此，取其中较低的k值作为谱聚类输入参数值。

通过自适应选取最优k值，得到进出山东威海港的部分典型轨迹如图9所示。

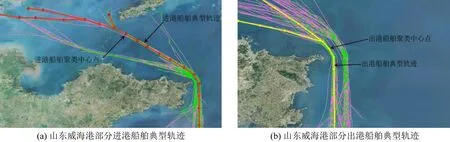
图9 山东威海港部分进出港的船舶典型轨迹Fig.9 Typical trajectories of ships entering and leaving Weihai Port,Shandong

3.3 船舶典型轨迹挖掘结果

通过东港海事和西港海事下载秦皇岛-泉州和泉州-秦皇岛的实际船舶航行数据。首先，把实际航行路线的经纬度数据转化为以WGS84为坐标系的经纬度；然后，利用点集转线把经纬度点转化为航线，并与自适应挖掘算法输出的典型轨迹进行对比。秦皇岛-泉州和泉州-秦皇岛的船舶航行路线如表2和表3所示。

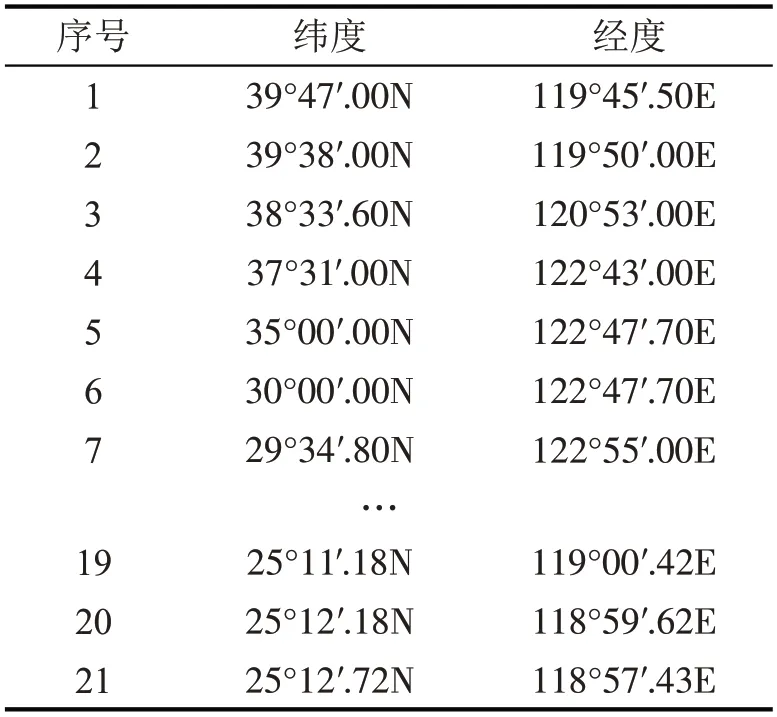
表2 秦皇岛-泉州船舶航行路线Table 2 Qinhuangdao-Quanzhou shipping route

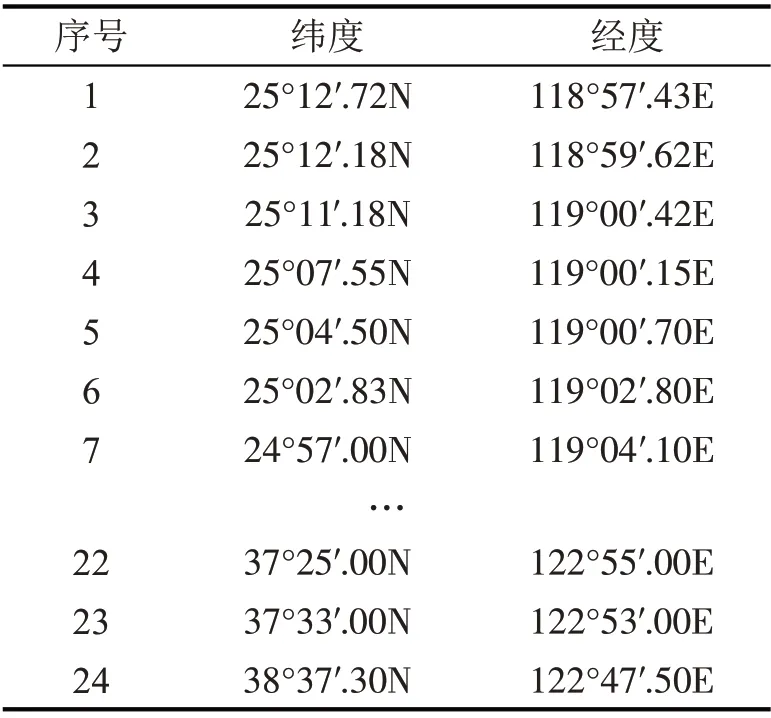
表3 泉州-秦皇岛船舶航行路线Table 3 Quanzhou-Qinhuangdao shipping route

实际航线轨迹图和通过自适应挖掘算法得到的典型轨迹如图10所示。

图10中，三角形连线是实际航行路线，圆形连线是自适应挖掘算法输出的典型轨迹。通过自适应挖掘算法输出的典型轨迹和实际的航线进行比较，结果符合船舶右侧行驶的特点，实际船舶航行路线与经过算法输出的典型轨迹基本一致，但是,也有略微的偏差，这是由于实际航行的船舶受到航行天气和周围其他船舶航行的影响，导致经过船舶AIS 数据聚类得到的典型轨迹与实际规定的航线有轻微的偏差。

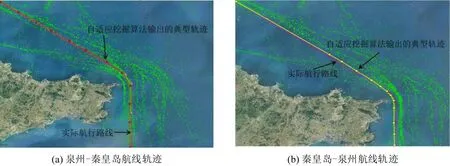
图10 实际航线轨迹图和自适应挖掘算法输出的典型轨迹Fig.10 Actual route track graph and typical track graph output by adaptive mining algorithm

3.4 与传统谱聚类算法的比较

利用传统谱聚类算法对相同的案例进行实验，比较两种算法的性能。原始船舶轨迹点如图11所示，图11中以虚线为界，进港船舶轨迹在虚线右侧的位置，出港船舶轨迹在虚线左侧的位置。

图11 未分簇的船舶轨迹Fig.11 Unclassified ship track diagram

为使传统谱聚类算法得到最佳参数，依旧采用基于Calinski-Harabaz 指标得分的方法。传统谱聚类算法Calinski-Harabaz 得分随k值的变化趋势如图12所示。

从图12 可知，随k值的上升，Calinski-Harabaz得分没有明显的上升和下降趋势，但在一个区间内产生了振荡，连续振荡后，在k=28左右出现了陡峭的尖峰，此时的Calinski-Harabaz 也是最大得分。选择k=28 作为传统谱聚类算法的输入参数，聚类效果如图13(a)所示。

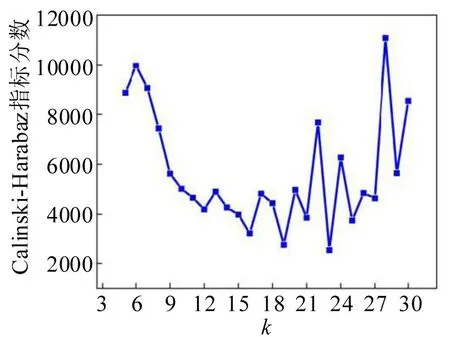
图12 传统谱聚类算法的Calinski-Harabaz得分变化Fig.12 Calinski-Harabaz score variation diagram of traditional spectral clustering algorithm

为证明改进的算法具有更好的聚类质量，在同等实验条件下，利用改进的谱聚类算法进行实验，实验结果如图13(b)所示。

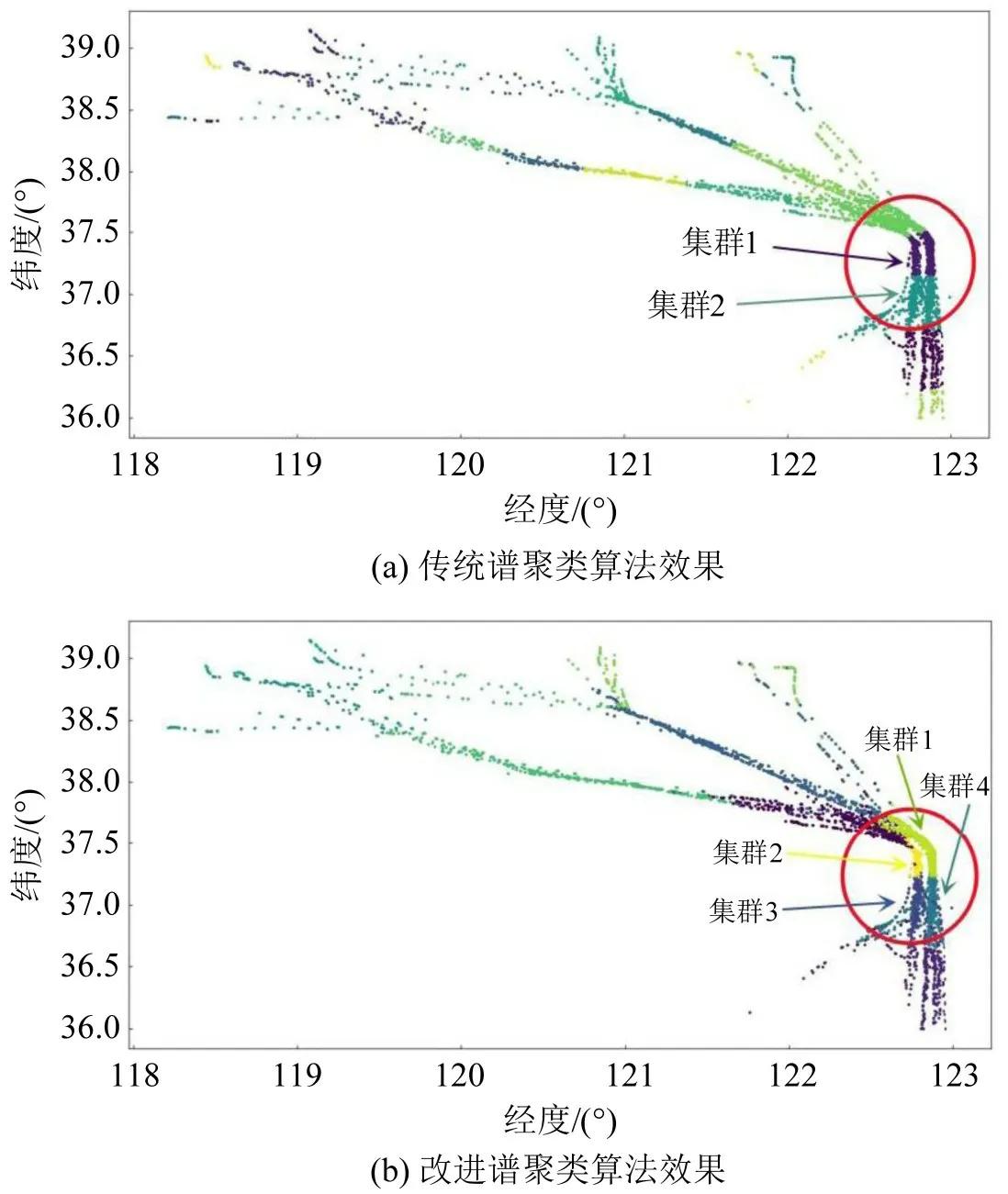
图13 聚类效果Fig.13 Clustering effect of spectral clustering algorithm

由图13(a)可以看出，传统谱聚类算法通过对所有船舶轨迹点组成的图进行切割，得到不同集群的切割图，各个集群的划分在视觉效果上感观良好。但在交通复杂的圆圈区域，传统聚类算法得到了两类集群(集群1 和集群2)。两类集群内部的进出港船舶轨迹相互穿插，这是由于传统谱聚类算法只根据船舶轨迹点的经纬度位置进行相似性度量，因此，在对山东威海水域的AIS 数据聚类时，出现了把进港船舶和出港船舶视为一类的情况。

由图13(b)可以看出，在交通复杂的圆圈区域，由于多属性相似性度量方法的引入，解决了进出港船舶视为一类的问题。将进港轨迹分为两类，分别是集群1 和集群4；出港船舶分为两类，分别是集群2 和集群3。对AIS 数据利用率越高，从中获得的资源信息就越多，说明改进谱聚类算法的优点是不言而喻的。

4 结论

在轨迹压缩方面，传统DP 算法只压缩形状属性，而忽略了船舶的航速和航向。对DP 算法进行改进，在压缩过程中依次压缩轨迹形状、对地航速和航向，保留了船舶航行的多维信息。在轨迹聚类方面，提出多属性相似性度量方法，相较于传统度量方法对AIS 数据有更高的利用率和更好的挖掘效果。考虑算法输入参数对聚类质量的影响，引入Calinski-Harabaz 指标。利用山东威海水域主航道的AIS数据进行实验，得到的船舶典型轨迹避免了只考虑对船舶位置点进行度量出现的进出港船舶轨迹视为一类的问题，且与海事局推荐的航行路线相比偏差较小，符合实际航行情况。