基于四元数的滚珠丝杠副载荷分布求解方法

罗飞 程红梁 凌维安 王超 张昭

(1. 南京航空航天大学，南京 210016；2. 博世华域转向系统有限公司，南京 210033)

0 引言

滚珠丝杠副作为一种传动装置，是汽车传动系统中常见的关键部件，同时也在机床加工、航空航天等领域中被广泛使用[1]。汽车转向器是汽车转向控制的重要零部件，该结构的受力形式极为复杂，有轴向力、径向力、弯矩等，这些力与力矩往往耦合作用，使运动副产生复杂变形，通过滚动体与滚道的挤压产生接触力；运动副的载荷分布直接关系着滚珠丝杠副的疲劳性能，只有在确定了运动副的载荷分布形后，才能进一步计算结构相关的性能参数，例如刚度、变形、接触应力等[2]。有限元法作为一种数值方法可以用来分析滚珠丝杠副，但是需要对模型进行较为复杂的前处理，耗时较长，不利于滚珠丝杆副的快速设计；因此，理论方法研究仍不可或缺。

滚珠丝杠副的载荷分布求解基于赫兹接触公式，需要计算滚珠-滚道挤压变形-压力的函数关系式，通过丝杠与螺母的相对变形描述滚珠的挤压。在传统的研究中，总是将滚珠与滚道的接触变形在某一个平面内把接触变形分解到接触点上，杨阳，陈蔚芳基于赫兹接触理论，在假设两个接触角(滚珠与丝杠的接触角以及滚珠与螺母滚道的接触角)相同的前提下，建立了相邻滚珠间的接触变形关系，并建立了滚珠载荷分布的数学模型[3]，张陈灵，范元勋建立了变形协调条件下的滚珠丝杠副载荷分布模型[4]。对于倾转变形的处理也是通过复杂的三角函数关系，变换到接触点上进行求解滚珠的挤压变形[5]。这种基于分解的思想太过复杂，公式推导也比较繁琐。四元数是一种在计算机图形学中被广泛使用的以描述矢量空间旋转的工具[6]，通过指定旋转轴，可以轻易将矢量的旋转转换为一个矩阵操作；四元数的应用在自动控制领域较多，孟德元提出了两类基于四元数表征的航天器全局姿态控制同步协议，保证了航天器姿态在物理意义下的全局同步[7]。陶庆凤基于四元数开发了一个机械手臂系统，以实现机械手臂姿态的快速解算[8]。

本文基于四元数求解滚珠丝杠副在复合受载下的载荷分布形式，将滚珠的与滚道相对变形中的倾转分量采用四元数描述，将滚道描述改写为参数曲线，并利用参数曲线的刚体位移计算滚珠的挤压变形，采用牛顿迭代法求解滚珠的载荷分布。

1 载荷分布模型

1.1 四元数的矩阵形式

四元数根据实部和虚部记作：

(1)

其中，标量s为实部，向量v为虚部。四元数运算内容较为繁杂，我们只用到其矩阵表示形式即可。

根据四元数相关知识，任意空间向量的旋转可以表示为对应四元数的运算。向量v1绕任意标准向量(单位向量)u按右手坐标系旋转θ角度后指向变化为v2，可以用四元数乘法描述，表示为：

v2=qv1q*

(2)

v1=[0,v1],v2=[0,v2]是实部为零的四元数，也称纯四元数。q为表示旋转的单位四元数，q*为q的共轭。q表示为：

(3)

将(3)式表示为矩阵乘法形式，令：

(4)

(5)

其中，θ为绕向量u转动的角度，[ux,uy,uz]T[ux,uy,uz]T为向量u的三个方向的分量。则转动矩阵可表示为：

(6)

对应向量旋转空间转动可以表示为：

v2=Q·v1

(7)

由图1易知，空间转动对应的四元数不是唯一的，对于任意向量，绕u方向旋转θ角和绕-u方向旋转2π-θ角所进行的变换是完全一致的。

图1 向量旋转示意图Fig.1 Vector rotation diagram

1.2 接触变形求载荷分布

静止/低速运动时滚珠丝杠副受力可以按静力学分析，滚珠处于静力平衡状态。一般认为滚珠与滚道的接触变形处于弹性范围内，满足赫兹接触假设前提条件；研究忽略滚珠滚道之间的摩擦力。由此滚珠受载后变形可以转化为滚道曲线之间的相对变形，假定螺母固定，丝杠相对螺母有变形量。

滚珠丝杠副的节圆半径为R0，滚珠半径为rb，内外圈滚道半径为ri、re，接触角β0，导程角为λ。可以推导出：

R1=R0-(re-rb)cos(β0)

(8)

R2=R0-(ri-rb)cos(β0)

(9)

其中，R1为外圈滚道参数圆曲线的半径,R2为内圈滚道参数圆曲线的半径。考虑到内外圈滚道偏移有：

(10)

(11)

(12)

(13)

L=R0tan(λ)

(14)

理想状态下滚珠球心运动路径沿着参数L0，L0的表达式：

x=R0cos(t)
L0∶y=R0sin(t),t∈[0,2π]
z=Lt

(15)

螺母滚道圆心参数曲线：

(16)

(17)

丝杠滚道圆心参数曲线：

(18)

(19)

(a) (b)图2 滚珠丝杠副坐标系及参数示意Fig.2 Coordinate system and parameter illustration of ball screw

上述参数曲线表明，四点接触的滚珠丝杠副螺母和丝杠各有两条参数曲线，上标N/S标明螺母/丝杠，下标L/R标明参数曲线对应滚道圆弧指向圆心的左右位置。在外载作用下，螺母和丝杠间发生相对位移，包括绕轴转动和三个平动。转动方向定义xoy在平面内，转轴角为φ，转动角度为θ，则对应转动四元数，图2描述了丝杠与滚珠的接触情况。

(20)

(21)

(22)

滚珠受到滚道挤压产生的变形量为变形前后的参数曲线间距离变化决定，变形前滚道参数线距离为：

A=re+ri-2rb

(23)

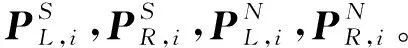
(24)

(25)

(26)

(27)

赫兹接触理论给出了接触变形与接触载荷关系，下式中K为刚度特性系数，计算式取决于接触点处的曲率参数、材料参数等。

δi1=max(Ai1-A,0)

(28)

δi2=max(Ai2-A,0)

(29)

(30)

(31)

对丝杠内部N个工作滚珠(不考虑反向器中的滚珠)，沿曲线参数值递增方向i=1,…,N为滚珠分解受力和力矩，可以得到：

(32)

(33)

挤压力的方向用空间单位向量表示：

(34)

(35)

函数unit()表示向量单位化。

上述推导建立了变形量—载荷分布——外载荷之间的递推关系。通常情况下是已知外载荷F0=[Fx0,Fy0,Fz0,Mx0,My0]T,未知变形量δ=[δx,δy,δz,φ,θ]和载荷分布。可通过牛顿迭代调整变形量使外载荷等于滚珠合力、合力矩。

2 验证算例

2.1 算例一

MESYS软件是由瑞士MESYS AG公司开发的专业滚动轴承计算分析软件，可以按照ISO/TS 16281标准计算滚珠丝杠副的载荷分布。某型号四点接触滚珠丝杠副参数见表1，根据本文的分析流程编写MATLAB程序计算丝杠的载荷分布，并与MESYS软件计算结果对比。

表1 某型号滚珠丝杠副参数

当给定外载[Fx0,Fy0,Fz0,Mx0,My0]T时(力单位：N；力矩单位：N·m)，基于本文算法和MESYS软件计算得到的载荷分布如图3所示。可见本文算法计算结果与软件计算结果基本吻合。

(a)

2.2 算例二

滚珠丝杠副在受载后会发生轴向/径向变形，而且受载后的载荷——变形关系并不是纯粹的线性关系。考虑到实际生产制造过程中，滚珠因各种因素不可避免会有制造误差，也需要考虑滚珠的几何公差。考虑几何误差只需要修正公式(27)～(28)，使变形量包含直径误差err，修改后的滚珠变形量计算值为：

δi1=max(Ai1-A+err,0)

(36)

δi2=max(Ai2-A+err,0)

(37)

其余分析过程完全一致，不需要做其他修改。图4计算了在不同误差下轴向变形随着轴向力的变化曲线，可以发现，不同误差的曲线起点不一样，这是因为当误差为正值时，滚珠与滚道是过盈配合，滚珠之间紧密贴合，受轴向力后滚珠间没有刚体位移，整体轴向变形为滚珠间的相对变形与滚珠滚道的相对变形的叠加；当误差为负值时，滚珠与滚道是间隙配合，整个滚珠丝杠副的轴向变形由滚珠与滚珠间的刚体位移以及相对变形与滚珠和滚道的相对变形叠加而成。因此，对于负值误差的曲线必然比正值误差的曲线要高，随着加载，滚珠之间受挤压后逐渐贴合在一起，刚体位移逐渐消失，在线弹性小变形假设下，整个结构的轴向变形的变化就趋于稳定。图5计算了在不同误差下随着径向力的变化引起的径向变形的变化，图5的曲线趋势大致与图4差不多，原因与图4的基本相同，此处不再赘述。

图4 轴向刚度Fig.4 Axial stiffness

图5 径向刚度Fig.5 Radial stiffness

3 结论

(1)基于四元数法建立了滚珠丝杠副在复合受载下滚珠与滚道的变形与载荷分布计算模型，将接触变形中的倾转部分表达为四元数的方式，能够很容易计算滚珠的变形量，在构建变形-载荷分布-外载的函数关系后，可以采用牛顿迭代法求解。

(2)针对不同的载荷形式，分别对比了本文算法以及MESYS的结果，两者基本吻合；考虑不同误差的情况下，通过将误差量叠加到变形上的方式，计算了滚珠丝杠副分别受轴向力与径向力逐渐加载的轴向变形以及径向变形；以上算例表明了本文算法的正确性以及适应性。