基于自适应锁相环的并网变流器暂态稳定提升策略研究
凌扬坚,付熙坤,黄萌,查晓明
(武汉大学电气与自动化学院,湖北 武汉 430072)
电力电子化电力系统具有非线性、多时间尺度、复杂性等特点,分析并网变流器的同步稳定性问题具有一定的挑战性[1-2].为了避免故障冲击下对电力系统的进一步恶化,通常会采取闭锁措施减小同步失稳变流器的影响.然而,随着电网中的可再生能源的比例不断增加,为了电网安全可靠地运行,必须要求变流器具备一定的抗干扰能力,不能任意锁闭.因此,保证变流器在大扰动后与电网同步稳定运行的能力显得尤为重要,这引发众多学者的关注.
文献[3-7]提出利用阻抗分析法、状态空间分析法、转矩分析法等经典方法以分析变流器的小信号稳定性问题.但是这些方法本质是将建立的模型线性化,只能分析工作点附近的稳定性,难以将这些分析方法直接用于分析大扰动下的暂态稳定性.
文献[8]指出,变流器同步的本质是电压平衡,通过旋转坐标系,将锁相问题转化为自动控制问题.在分析同步发电机的暂态稳定性时,通常使用等面积法则,由于同步发电机转子运动方程与变流器控制方程的高度相似,等面积法则也被推广至变流器的暂态稳定性分析中,能够直观地揭示锁相环(Phase-Locked Loop,PLL)或虚拟同步控制的暂态失稳机理[9-13].但是只有当同步单元的频率与输入偏差满足积分关系时,等面积法则才能使用[10-11].在PLL中,由于PI调节器的比例环节会产生阻尼项,使用等面积法则可能会导致对系统的稳定性分析不准确.相图法也是分析变流器暂态稳定性的有效手段,通过动态方程相图的敛散性,可以得到变流器的稳定域[1,14].相图法的本质是一种数值方法,对参数集进行分析,结果不具有普遍性,但是通过相图可直观判断系统的稳定性,可用于结果分析.此外,能量函数法也是一种分析变流器暂态稳定性的有效方法[15-17],在满足李雅普诺夫函数条件时,通过比较函数值与临界值的关系,从而判断变流器的稳定性,但是如何构造合理的能量函数是一个难题.
研究暂态稳定性的先决条件是需要满足稳定工作点的要求,即存在稳定平衡点[11,13].只要存在平衡点,一阶PLL就可以有效缓解电网扰动带来的同步丢失问题,但是当电网频率偏离它的额定值时,存在稳态相位跟踪误差.传统的PLL引入了二阶非线性摆动方程,根据并网点(Point of Common Coupling,PCC)处的电压,实现对电网频率和相位的跟踪.但是扰动发生时,即使存在稳定平衡点,系统也存在失去同步的风险[13,15].为了提升变流器在扰动期间的暂态稳定性,文献[18]通过等面积法则得到有功电流和无功电流的稳定域,提出限制电流边界的稳定控制策略,但是对于不同的扰动,需要设置不同的参考电流;文献[19]在扰动期间检测PLL输出角的变化率,反馈到PI调节器的输出,减缓输出角的变化,与传统PLL相比,这会延长暂态过程;文献[20]在扰动期间直接关闭PLL的积分环节,使其成为一阶PLL,这容易造成相位跟踪不准确.
因此,为了提升变流器的暂态稳定性,本文对传统PLL建立数学模型,基于能量函数的得到变流器的暂态同步稳定判据,并在此基础上设计一种自适应PLL控制策略,使其面对不同的扰动均能提高暂态稳定性,并尽可能保证准确的相位跟踪能力.
1 并网系统的建模
1.1 并网系统
变流器的并网结构如图1(a)所示,其中,udc为风光发电输出的直流电压,Ig为并网电流的峰值,VPCC是PCC处的电压峰值,Zg为电网阻抗,Vg为电网电压峰值,VSC为电压源型变流器模块,Lf为滤波器的电感,对变流器输出的波形进行滤波,传统PLL的控制结构如图1(b)所示,θPLL表示PLL的锁相角,ωg表示电网额定角频率,Kp和Ki分别是PLL的比例系数和积分系数,Idref表示参考有关电流,Iqref表示参考无功电流.

图1 并网系统及传统PLL结构
由于电流环的时间尺度远小于PLL的时间尺度,因此可以忽略并网电流Ig在暂态过程的变化.因此,可以假设为电流环为恒定的增益环节,图1的并网系统简化成图2.其中,φ表示并网电流Ig相对于锁相角θPLL的相位差;Zg表示电网阻抗;θZ表示电网的阻抗角;θg表示电网电压相位.

图2 并网系统简化电路图
1.2 并网系统的数学模型
根据PLL的结构,可以得到PLL的动态方程:
(1)
根据图2,VPCCq可以表示为
VPCCq=VZq+Vgq
,
(2)
公式中:VZq为并网电流Ig流过电网阻抗Zg时在同步旋转坐标系的q轴电压降分量;Vgq为电网电压Vg在同步旋转坐标系的q轴电压分量.
在弱电网中,电网电抗远大于电阻,因此忽略电阻的影响,即电网阻抗Zg=jXg.控制并网电流与PLL的差角为零,即φ=0,此时Igd=Ig,Igq=0.因此可以得到VZq和Vgq:
(3)
将锁相角θPLL与电网电压相位θg的角度差记为δ,根据公式(1)~公式(3),可以得到:
(4)
在暂态过程中,并网电流的相位随着锁相角变化,因此并网电流的频率也在变化,即电网的电抗部分对外表现为动态变化,即
(5)
根据公式(4)和公式(5)可以得到PLL的二阶微分方程:
(6)
公式中:M=1-KpIgLg;P10=KiIgωgLg;P11=KiVg;D=KpVgcosδ-KiIgLg.
PLL的控制方程与同步发电机的转子运动方程相似,可将M视为“等效惯性时间常数”;P10视为“等效机械功率”;P11视为“等效电磁功率”;D视为“等效阻尼系数”.由公式(6)所示,PLL的比例系数和积分系数、并网电流、电网阻抗和电网电压共同影响PLL的暂态稳定性.
2 暂态稳定性分析
2.1 能量函数的构造
通过观察公式(6)可以发现,PLL的二阶微分方程与同步发电机的转子运动方程相似,在构建PLL的能量函数过程中,忽略阻尼部分,通过首次积分法构建合适的能量函数.
对公式(6)忽略阻尼部分,并在等号两边同时乘以dδ/dt:
(7)
对公式(7)进行积分:
(8)
根据公式(8),定义PLL的动能Ek1和势能Ep1分别为
(9)
公式中:E1为一个常数.
因此,PLL的能量函数可以表示为
(10)
根据公式(6)和公式(10),能量函数的导数可以表示为
(11)
2.2 阻尼对稳定域的影响
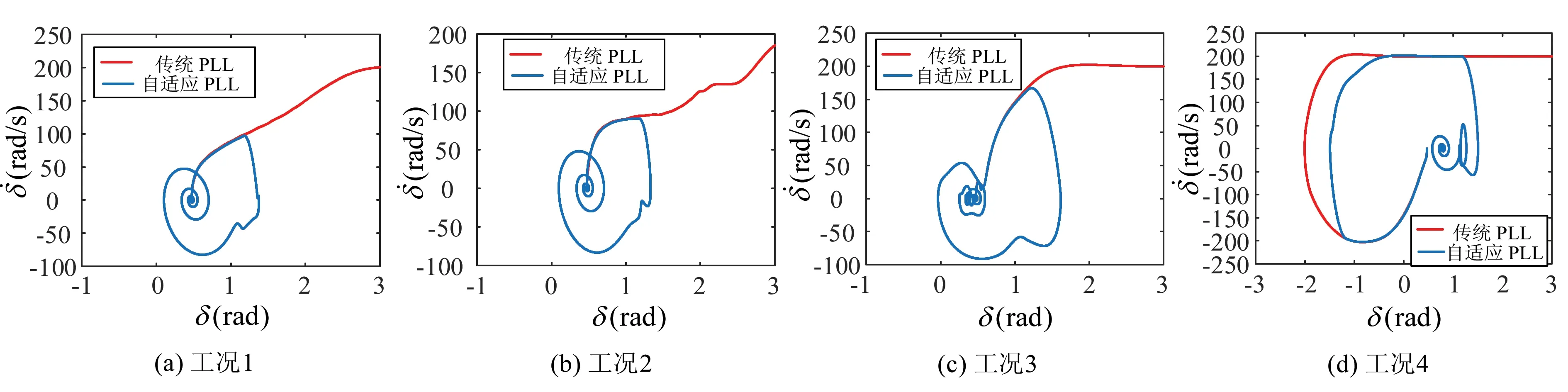
在不考虑等效阻尼系数D的变化时,能量函数需要满足dV/dt< 0的条件.在暂态过程中,PLL的动能Ek1和势能Ep1相互转化.如果PLL的总能量V1小于最大势能Epu1,在阻尼作用下,最终PLL能够恢复稳定,保持与电网同步运行,即系统受到大扰动时,保证扰动切除时系统的总能量Vcr1 在一个确定的系统中,等效阻尼系数D会随着δ变化,它是一条向下平移后的余弦曲线.当出现等效阻尼系数D<0时,导致暂态过程中会出现dV/dt> 0,因此不能保证系统在受到大扰动时恢复稳定.在暂态过程中必需保证等效阻尼系数D>0,根据公式(7)可以得到δ的最大变化范围: (12) 根据公式(9)和公式(12),可得到等效阻尼系数D对稳定域的影响,如图3所示.在δmax对应的势能为Epmax,在暂态过程中,如果系统的势能Ep1 图3 等效阻尼系数对稳定域的影响 等效阻尼系数D会影响系统的暂态稳定性,为了提高系统的暂态稳定性,需要选择合适的参数,增大等效阻尼系数D,达到增大系统稳定域的目的.根据公式(7)所示,通过改变Kp、Vg、Ki、Ig、Lg等参数,可以增大等效阻尼系数D.然而这些参数也会影响P10和P11,从而影响系统的暂态稳定性.需要指出的是,对于一个确定的系统,这些参数无法改变,并且改变这些参数并不能从本质上解决等效阻尼系数D出现负数的情况.因此,为了避免发生出现负阻尼D的情况,本文通过改变PLL的结构,达到优化PLL暂态稳定性的目的. 根据公式(7)所示,如果将PLL的积分系数Ki设置为零,只要δ不超过π/2,就可以保证等效阻尼系数D非负,从而保证系统暂态稳定.但是如果关闭PLL的积分环节,PLL将由二阶变成一阶,只要系统存在平衡点,一阶PLL就可以缓解由扰动带来的同步失稳问题,但是当电网偏离它的额定值时,存在稳态跟踪误差,因此不能直接关闭PLL的积分环节.为了避免出现等效阻尼系数D出现负数,本文设计了一种自适应PLL,当等效阻尼系数D出现负数时,关闭PLL的积分环节.这种自适应PLL既可以提高系统的暂态稳定性,也可以保证系统在稳定工作时的相位跟踪能力,自适应PLL结构如图4所示. 自适应PLL的基本原理:在系统受到大扰动时,如果系统的等效阻尼系数D≥0,不改变PLL的结构,保留其积分环节;如果系统受到严重的扰动,导致δ的变化超过传统PLL允许的最大范围δmax,出现等效阻尼系数D<0,此时PLL的结构发生变化,PLL会关闭PI调节器积分环节,二阶PLL将会切换到一阶PLL.自适应PLL的切换逻辑如图5所示. 图4 自适应PLL结构图5 自适应PLL的切换逻辑 当等效阻尼系数D<0时,自适应PLL变为一阶PLL,其结构发生变化,构造的能量函数也发生变化.根据自适应PLL结构,可以得到PLL的δ运动方程: (13) 根据公式(13),可以得到PLL的二阶微分方程: (14) 其中, (15) 根据公式(14),可以定义自适应PLL的动能Ek2和势能Ep2分别为 (16) 因此自适应PLL的能量函数: (17) 由公式(14)和公式(17)可以得到自适应PLL的能量函数的导数: (18) 由公式(18)所示,改进PLL后系统能量函数的导数非正,增大了系统的稳定域.只要在受到大扰动时,系统的总能量V2小于系统的最大势能Epu2,系统就可以恢复稳定.自适应PLL的稳定域如图6所示,与传统PLL的稳定域相比,自适应PLL的稳定域增大,由原来的红色虚线包围的区域,增大为蓝色实线包围的区域. 图6 自适应PLL的稳定域 在MATLAB/Simulink中搭建如图1所示的变流器系统,对其进行仿真验证,仿真参数如表1所示. 表1 系统参数 为了验证自适应PLL的性能,基于以上参数,本文设置了电网电压跌落,并网电流扰动,电网电感扰动和电网频率扰动四种仿真工况,如表2所示. 表2 仿真工况 各种工况均在t=0.5 s发生扰动,并在0.02 s后清除扰动,图7至图8是4种工况下的相图和时域图仿真结果,对比了自适应PLL与传统PLL在面临大扰动下的暂态结果. 这4种类型的扰动,均会出现等效阻尼系数D<0的情况,即δ超出临界值1.175 rad(即δmax),因此传统PLL不能恢复稳定,其相图发散.对于本文提出的自适应PLL,δ超过临界值1.175 rad时,自动关闭积分环节,避免出现等效阻尼系数D<0的情况;δ向稳定工作点移动,小于临界值1.175 rad时,自动重新启动积分环节,提高PLL的相位跟踪能力.因此,自适应PLL的相图轨迹会至少发生两次变化,如图7(a)~图7(c)所示. 图7 4种工况下PLL的相图 当电网频率低于50 Hz,电网阻抗减小,其对应的稳定工作点减小,因此δ向负半轴移动.因此,δ小于-1.175 rad时,自适应PLL自动关闭积分环节;当其逐渐增大,超过-1.175 rad时,自适应PLL自动重新启动积分环节.因此,图8(d)多次改变轨迹.系统重新恢复稳定后,没有回归初始稳定工作点δ0,是由于电网频率发生改变,导致电网电压相位发生变化.与工频电网相比,在0.02 s内,系统滞后了0.314 rad,即电网电压的初相位为-0.314 rad,因此δ增加0.314 rad,新的稳定工作点由原来的0.472 rad变为0.786 rad. 图8 4种工况下PLL的相角时域图 以上仿真结果表明,自适应PLL可以提升系统的暂态稳定性,更大限度地容忍各种工况的扰动,验证了自适应PLL的合理性. 本文通过首次积分法建立了变流器暂态能量模型,发现了等效阻尼系数对系统暂态稳定域的影响关系:当系统轨迹在正阻尼范围内运动时,系统能量耗散,使得系统恢复同步;当系统在负阻尼范围内运动时,系统的能量会逐渐增大,并最终超过势能边界,导致系统失去暂态稳定性.为避免出现等效阻尼系数为负的情况,本文设计一种自适应PLL,通过检测功角的变化自动关闭PLL的积分环节,通过抑制负阻尼的不利影响,提升了系统的暂态稳定性.相应的仿真结果验证了自适应PLL的有效性.
3 PLL的改进
3.1 自适应PLL的设计

3.2 自适应PLL稳定性分析

3.3 自适应PLL的效果



4 结 论

