一种灵活抗多普勒的MIMO雷达波形设计

王家伟，沈炳声，罗荣

(西南交通大学数学学院，四川 成都 611756)

0 引言

多输入多输出(MIMO)雷达具有多个发射和接收天线，各发射天线发射不同信号，从而具有波形分集能力.与传统雷达相比，MIMO雷达系统具有更高的发射自由度，这提升了MIMO雷达系统在目标检测、高分辨率、参数估计等方面的性能.针对不同的工作场景和环境信息需要设计不同的发射波形，MIMO雷达波形设计是一个重要的研究领域[1-2].

相位编码技术以其冗余度高的特点被大多数学者作为波形设计的研究对象[3].该方法应用序列对长脉冲进行相位编码，利用匹配滤波后的相关函数作为波形设计的评判标准.基于Heimiller多相序列[4]、Frank码[5]、Chu多相码[6]、Barker序列[7]以及Golomb和Scholtz构造的广义Barker序列[8]，可以得到良好的周期自相关函数.然而，在雷达中通常考虑非周期相关函数.因此，在相位编码波形的设计中，幺模互补序列集被广泛应用.例如Marcel Golay[9]提出的Golay互补序列(GCP)，Tseng和Liu[10]提出的互补序列集，Sivaswamy[11]和Frank[12]提出的多相互补序列集.这些序列集的共同点在于非周期自相关之和在零时延以外处处为零.但是，互补集相位编码生成的波形在经过匹配滤波器后仅在零多普勒轴上没有距离旁瓣，在零多普勒轴以外会有相当大的距离旁瓣，这对移动的目标检测会产生较大的干扰.因此，通过相位编码设计灵活抗多普勒的互补波形十分有意义.

针对上述问题，文献[13]中提出基于Golay互补序列编码的雷达波形设计，其通过PTM序列控制Golay互补波形的发送顺序，从而消除了模糊函数在零多普勒轴附近的距离旁瓣.在此基础上，文献[14]中基于SDAMM算法搜索准正交Z-互补对(QOZCP)，并且提出基于QOZCP的全极化雷达波形，该波形经过匹配滤波后的互模糊函数优于Golay互补序列编码的全极化雷达波形，但是其优化算法的复杂度较大，计算储存量较大.文献[15]中在Golay互补序列与PTM序列的基础上提出基于完备互补码(CCC)和GPTM序列的MIMO雷达波形，利用CCC相关特性消除不同波形互相关的干扰并且自相关具有极低的距离旁瓣.但以上方法仅适用于微小的多普勒失配，无法实现MIMO雷达系统中更广泛移动目标的探测.此外，文献[16]中利用过采样PTM序列控制Golay互补序列的发送顺序，能使模糊函数在特定频率附近有效降低距离旁瓣，实现了单天线以及全极化天线下灵活对抗多普勒频移.

本研究在文献[16]的基础上，基于完备互补码，构造出MIMO雷达适用的灵活多普勒容忍波形.根据MIMO雷达系统的发射天线数目可以灵活选择完备互补码波形的矩阵大小，有效降低各发射波形之间的时域互相关.最后，仿真验证表明所提出的MIMO雷达波形模糊函数在特定多普勒频率附近具有极低的距离旁瓣.该方案的灵活性是已有波形设计方案无法比拟的.

1 预备知识

定义1复值序列a=(a0,a1,…,aL-1)和b=(b0,b1,…,bL-1)的非周期互相关函数(aperiodic cross correlation function,ACCF)定义为：

(1)

特别地，当a=b时，称Ra,a(k)为非周期自相关函数(AACF)，简记为Ra(k)，其中上标*表示复共轭.

定义2设序列集C={c0,c1,…,cN-1}，其中ci表示长度为L的序列，若

(2)

则称c为互补序列集.当N=2时，称c为格雷互补序列对(golay complementary pair,GCP).

定义3假设序列族X={c1,c2,…,cM}，其中cm={cm,0,cm,1,…,cm,N-1}是一个大小为N的互补序列集，包含N条长度为L的序列.若

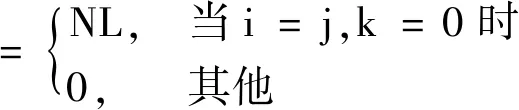
(3)

则称X为正交互补序列集(mutually orthogonal complementary sequence Set,MOCSS)，记为(M,N,L)-MOCSS.

引理1[17]对于一个正交互补序列集，其族的上界满足：

M≤N.

特别地，当M=N时，MOCSS被称作完备互补码(CCC)，记为(N,L)-CCC.

定义4p元GPTM序列(vp(n))n≥0:

1)vp(0)=0;

2)vp(n)=mod(tp(n),p).

其中，tp(n)等于整数n的p进制表示时各位数字之和，mod表示求余函数.

关于p元GPTM序列，存在如下引理，该引理将用于本文中的MIMO雷达波形设计.

引理2[18]对于L=pM+1，其中p,M是两个正整数，定义序列S(L)=(0,1,…,L-1).定义{S0,S1,…,Sp-1}是S(L)的由GPTM序列得到的p块分区，其中Si={n∈S(L)|vp(n)=i}，则对于u=0,1,…,M，有：

(4)

2 信号模型

2.1 相位编码与模糊函数相位编码信号由于其大时宽带宽积而被广泛应用于雷达发射信号中，通过在不同脉冲重复间隔(PRI)进行离散相位编码，可以提高雷达距离分辨力和多普勒分辨力.本研究通过脉冲串的模糊函数图像来判定波形的优劣,模糊函数的定义请参考文献[16].

对于序列a=(a0,a1,…,aL-1)，在一个脉冲中通过相位编码后的基带波形表达式为

(5)

其中，Ω(t)是持续时间Tc的单位能量脉冲形状函数，Tc是码片长度.sa(t)的模糊函数χsa(τ,v)表示为

(6)

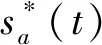
在发射天线上需要通过多个PRI构成发射波形，假设一个PRI的长度为T，由于持续时间Tc相对T非常小，所以脉内多普勒效应可以忽略[16].假定目标运动速度恒定，则相邻PRI 的多普勒相移为常数.若在单天线上选择发射序列集C=(c0,c1,…,cN-1)，发射信号的表达式为

sC(t)=sc0(t)+sc1(t-T)+…+scN-1[t-(N-1)T]

(7)

由于是单天线，所以只考虑自模糊函数，其表达式为

(8)

在考虑模糊函数时忽略不同PRI回波之间的混叠效应，利用相邻PRI之间恒定的相位差代表目标恒定的速度，忽略Ω(t)的影响并且将时延离散化[16]后，其自模糊函数表示为

(9)

其中，k表示时延，θ表示多普勒频移.

在考虑多天线时，不仅需要考虑自模糊函数，还需要考虑互模糊函数，假设其中第i根与第j根天线分别发送序列集Ci=(ci,0,ci,1,…,ci,N-1)和Cj=(cj,0,cj,1,…,cj,N-1)，其互模糊函数表示为

(10)

图1 MIMO雷达信号模型

3 基于完备互补码编码的MIMO雷达波形设计

在MIMO雷达系统中，我们不仅要考虑降低波形自相关旁瓣，也要考虑消除波形间的互相关影响.已有工作中的方法只适用于零多普勒轴附近降低距离旁瓣，本研究不仅在零多普勒频率附近有效地降低距离旁瓣，并且实现了在特定的多普勒频率附近显著降低距离旁瓣.

对于p根天线的MIMO雷达系统，文献[15]中选择的完备互补码(p,L)-CCC由p个互补集构成，每个互补集中包含p条序列.每根天线分配一个互补集，其中第i根天线发射的波形由互补集Ci={ci,0,ci,1,…,ci,p-1}组成，每根天线上序列的发送顺序都由同一个p元的GPTM序列控制.

以p=4为例，第i根天线发射的序列取自Ci={ci,0,ci,1,…,ci,3}.而4元GPTM序列表示为：

(0,1,2,3,1,2,3,0,…).

在4元GPTM序列的控制下，第i根天线发射的序列顺序为：

(ci,0,ci,1,ci,2,ci,3,ci,1,ci,2,ci,3,ci,0,…).

通过长度4M+1的4元GPTM序列控制互补集中序列的发送顺序，只能实现和文献[15]中同样的效果，使得在接收端得到的组合模糊函数在θ=0处的泰勒展开式的前M项被消除，从而在零多普勒附近实现极低的距离旁瓣.

现在我们可以设计一种在多普勒频率θ0=2πl/m附近有效抗多普勒的MIMO雷达波形，其中l和m是两个互质的整数，l≠0且m≠1，步骤如下：

步骤1当一个MIMO雷达具有p个发射天线时，选择(p,L′)-CCC中的序列作为编码对象，(p,L′)-CCC={C1,C2,…,Cp}，通过矩阵表示如下：

其中第i行表示互补集Ci中的p条序列，1≤i≤p.

步骤2第i个发射天线的编码序列取自Ci={ci,0,ci,1,…,ci,p-1}.这里先定义一种(pM+1,m)-GPTM序列，该序列表示的是将长度为pM+1的GPTM序列每个元素重复m次.通过(pM+1,m)-GPTM序列中的元素协调相位编码波形中每个PRI中编码的序列，第i个发射天线上序列的编码顺序Ti为

这些序列通过相位编码后构成发射信号.一共p个发射天线，每个天线上的发射信号包含pM+1×m个编码序列.利用矩阵表示为：

其中，不同的行代表不同的天线，不同的列代表不同的PRI.

基于以上的波形构造方法，提出以下两个分别关于自模糊函数和互模糊函数的定理，进而证明波形具有灵活抗多普勒的性质.

定理1(c0,c1,…,cp-1)是一个大小为p的互补序列集，考虑使用一个(pM+1,m)-GPTM序列控制互补集生成脉冲串，即

则自模糊函数χT(k,θ)在θ0=2πl/m处有M阶零点.

定理1的证明首先考虑m=1时，每个PRI上的采用的波形由L=pM+1的p元GPTM序列控制：

T=(cvp(0),cvp(1),…,cvp(L-1)),

则PRI中对应的编码序列的非周期相关函数可以表示为Rn(k)=Rvp(n)(k).当时延k固定时，Rn(k)一共有p种取值.对于非负整数i∈[0,2p-1-1]，其二进制表示为

(11)

(12)

(13)

当u=0,1,…,M时，结合引理2，有

(14)

其中，R0+R1+…+RP-1=B0.在式(14)的基础上，结合互补序列集的性质，有

(15)

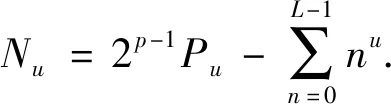
当m≠1时，波形的自模糊函数为

(16)

令

(17)

由于B0=R0(k)+R1(k)+…+Rp-1(k)，根据互补序列集的性质，χT(k,θ)的距离旁瓣只由hp(θ)决定.如果能将hp(θ)在θ0处的泰勒展开式前M项消除，则能证明自模糊函数θ0处具有M阶零点.将hp(θ)在θ0处进行泰勒展开：

(18)

所以只需要证明设计的T满足当t=0,1,…,M时，有

(19)

由式(17)求导得

(20)

对(nm+z)t进行二项式展开，有

(21)

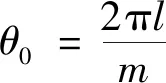
(22)

结合定义2，当(c0,c1,…,cp-1)是一个大小为p的互补序列集时，有

(23)

所以当t=0,1,…,M时，式(19)成立，从而证明出χT(k,θ)在θ0处具有M阶零点.

基于上述定理，自模糊函数χT(k,θ)在所有的多普勒频点θ0=2πl/m有M阶零点，进而实现距离旁瓣的抑制. 接下来考虑两根天线上互模糊函数的影响.

定理2对于两个大小为p的互补集(ci,0,ci,1,…,ci,p-1),(cj,0,cj,1,…,cj,p-1)，考虑使用一个(pM+1,m)-GPTM序列控制互补集生成脉冲串，即

则Ti和Tj的互模糊函数χTi,Tj(k,θ)在θ0=2πl/m处有M阶零点.

根据CCC的性质，可以得到和自模糊函数相似的结论，互模糊函数在θ0处有高阶零点，在一定的频率范围内显著压缩了距离旁瓣.

在上述两个定理中，当取l=0,m=1时，对应于文献[15]中基于CCC和GPTM序列的MIMO雷达波形，该波形仅在零多普勒附近有效降低距离旁瓣.本研究任意选取两个互质的l和m，在过采样GPTM序列的作用下，所得到的MIMO波形可以在特定的多普勒频率附近实现低的距离旁瓣，进而达到灵活抗多普勒效果.

4 仿真实验

本研究仿真采用收发同置、发射阵元和接收阵元均为4的集中式MIMO雷达系统.为分析本文中波形的性能，主要以模糊函数中期望频点附近的旁瓣高低为考察标准.

设定l=1,m=2，即θ0=π.仿真选取(4,32)-CCC，在4根发射天线上各分配一个大小为4的互补集，利用(44,2)-GPTM序列控制互补序列的发送顺序，发射信号的波形矩阵表示为：

其中，不同的行代表不同的天线，不同的列代表不同的PRI，共512个PRI.

为了研究本文中波形在多普勒频率π附近的性能，与文献[15]中所设计的波形、交替发送的波形进行比较.对于交替发送的波形，第i根天线上的波形由(ci,0,ci,1,ci,2,ci,3)重复128次构成，共512个PRI.由于文献[15]中要求每个发射天线上PRI数目须为4的正整数幂，无法选取512个PRI方案，故选择长度为45的GPTM序列控制互补序列的发送顺序，共1 024个PRI.

图2 不同波形在多普勒频率θ0=π附近自模糊函数

从图2(c)中可以看出，与交替发送的方案对比，自模糊函数的旁瓣被抑制到-60 dB以下；与文献[15]中的方案对比，本研究方案只消耗一半的时间资源，波形自模糊函数距离旁瓣在多普勒频率范围[π-0.05,π+0.05]内被抑制到-50 dB以下.

图3 不同波形在多普勒频率θ0=π附近互模糊函数

从图3(c)中可以看出，与交替发送的方案对比，互模糊函数的旁瓣被抑制到-60 dB以下；与文献[15]中的方案对比，本文中方案只消耗一半的时间资源，波形自模糊函数距离旁瓣在多普勒频率范围[π-0.05,π+0.05]内被抑制到-50 dB以下.

此外，本文中所构造波形不仅可以在多普勒频率θ0=π处有效对抗多普勒，还能在零多普勒轴附近显著抑制距离旁瓣.从图4可以看出，本文中波形的自模糊函数和互模糊函数的距离旁瓣在多普勒频率范围[-0.05,0.05]内被抑制到-60 dB以下，这与文献[15]中的结论是相同的.

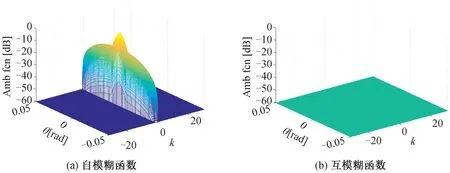
图4 中波形在多普勒频率θ0=π附近模糊函数的仿真

图4是本文中波形在多普勒频率θ0=π附近模糊函数基于以上的仿真，本研究所提MIMO雷达波形与文献[15]中的波形、交替发送的波形相比，在特定的多普勒频率下，有更好的自模糊函数与互模糊函数.此外，由于m与l的任意性，本文中波形可以在任意多普勒频率θ0=2πl/m处抑制距离旁瓣.综上，本文中波形不仅可以在零多普勒轴附近有效对抗多普勒，并且实现了在任意的多普勒频率附近显著压缩距离旁瓣.

5 结论

基于过采样GPTM序列和完备互补码提出一类灵活抗多普勒的MIMO雷达波形，该波形利用完备互补码和过采样GPTM序列的性质在任意的多普勒频率附近明显降低了雷达回波的距离旁瓣.仿真结果表明利用本文中构造的波形后，能够赋予波形灵活抗多普勒的性质，更有利于实际场景中的应用.