泥石流作用下双柱桥墩动力响应研究

李 聪，邹 强，雷 雨，蒋 虎，周 斌，胡 镇 汝

(1.中国科学院水利部 成都山地灾害与环境研究所，四川 成都 610041； 2.中国科学院大学，北京 100000； 3.成都理工大学 地球科学学院，四川 成都 610059)

0 引 言

山区复杂的地形地貌和集中的强降雨为泥石流的发生提供了丰富的物质基础和水源条件[1]。泥石流作用于已建桥梁常造成巨大损失。而桥墩作为桥梁的主要承重构件，常受泥石流直接冲击作用，因此研究泥石流对桥墩的作用机制，对桥墩风险防控和防灾减灾工作的开展具有重大指导意义。

泥石流对桥墩的破坏方式主要有冲刷、淤埋、振动和冲击破坏，其中冲击破坏为桥墩的主要破坏方式[2]。众多国内外学者开展了泥石流对桥墩的冲击过程研究。王东坡等[3]开展了泥石流冲击桥墩的物理模型试验，该研究分析了泥石流流速、流深以及流体特征参数与泥石流冲击压力的相关性。王林峰等[4]运用动力学中的弹性碰撞理论和牛顿第二定律对泥石流冲击力进行了修正并总结了山区桥梁的破坏模式及损毁机制。姚昌荣等[5]以既有铁路重力式桥墩结构作为研究对象，采用ANSYS+CFX建立了泥石流冲击桥墩的流固耦合分析模型，分析了桥墩在不同参数的泥石流冲击作用下的响应情况。Liang等[2]通过对泥石流流深和流速的不同组合建立了150组泥石流冲击桥墩的数值模型，使用非线性有限元方法建立了泥石流动量通量和超越概率之间的易损性曲线。Yan等[6]提出了泥石流作用下基于非线性结构分析的桥墩易损性分析方法，该方法采用泊松方波过程和泊松脉冲过程表征泥石流冲击，通过蒙特卡洛抽样建立不确定性评估模型。以上研究多针对单柱桥墩进行试验或者数值模拟，且在研究过程中未考虑大石块的瞬间冲击作用，但泥石流冲击双柱桥墩时因其前后柱体会对流场产生影响，因此其流场动力过程不同于单柱桥墩。而双柱桥墩因其抗侧刚度大、材料耗损小而广泛存在于中国山区中，因此合理反演泥石流冲击作用，研究双柱桥墩的动力响应机制具有重要意义。

本文基于单向流固耦合理论，对泥石流流场动力过程采用有限体积法计算，石块冲击则使用接触有限元方法模拟，通过将流场计算得到的泥浆冲击压力时程叠加大石块冲击作用来反演泥石流完整冲击过程，最后基于有限元方法求解桥墩动力响应。

1 泥石流冲击桥墩模型

本文所采用的桥墩模型为对G213线某桥梁进行的等比例建模，如图1所示。流体流域为11.5 m×8 m×7 m的立方体，底部4 m为泥石流流域，顶部3 m为空气流域。流域中心放置双柱桥墩，桥墩正前方放置半径1 m的球形石块。双柱桥墩墩高11.6 m，直径0.9 m，两墩中心间距3.5 m，系梁截面高0.7 m，宽0.4 m，基础为刚性基础。混凝土为C35，保护层厚度为40 mm，纵筋采用HRB400，18@32；箍筋采用普通箍筋HRB335，B14@200。几何模型如图2所示。

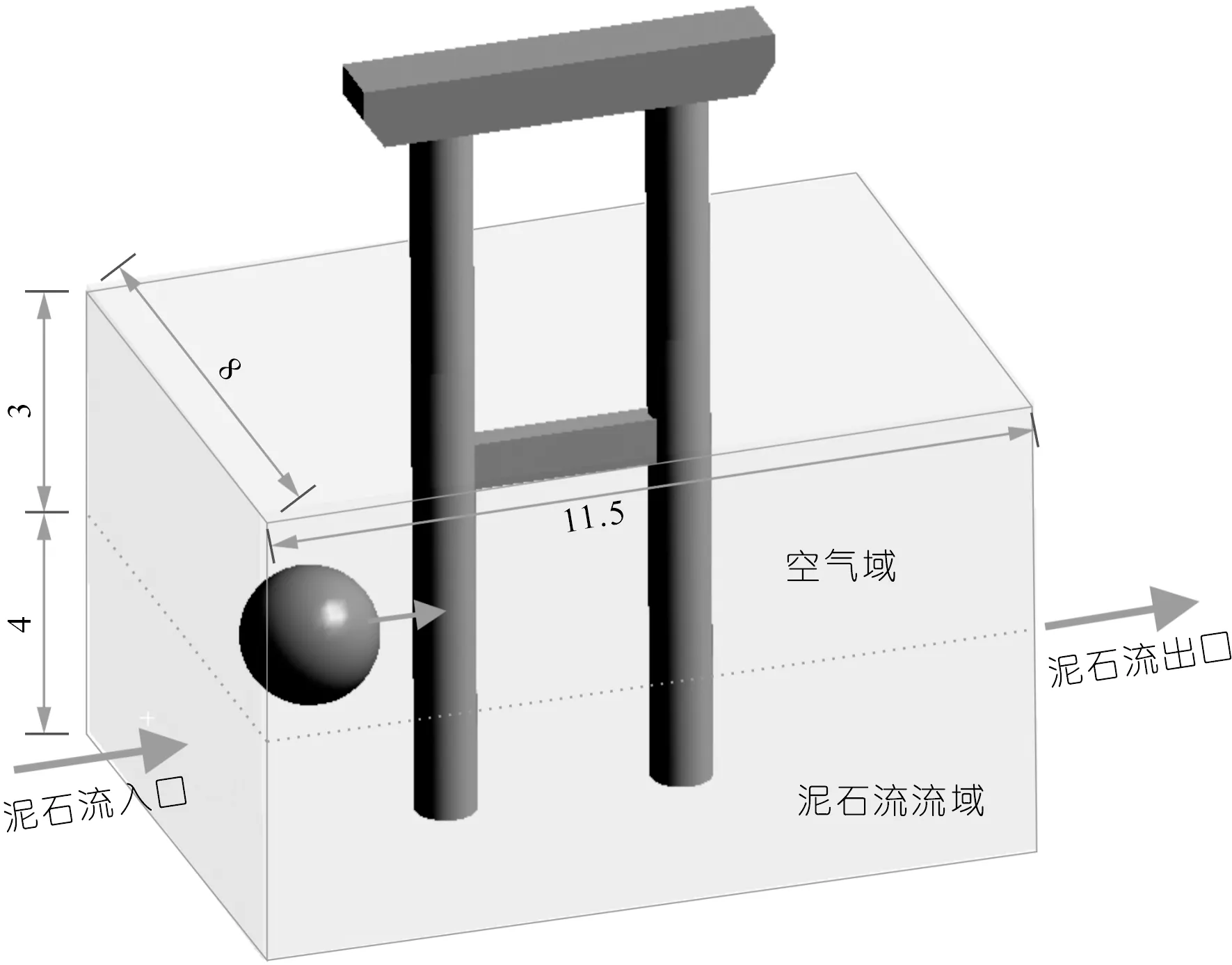
图1 泥石流冲击桥墩模型(尺寸单位：m)

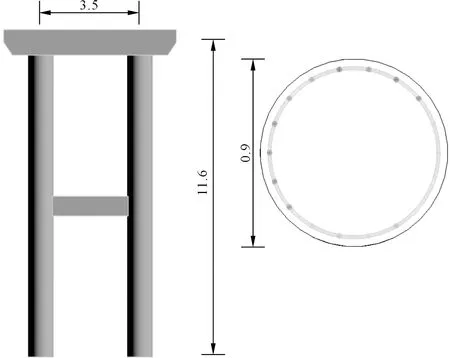
图2 桥墩模型及其截面配筋(尺寸单位：m)

1.1 泥石流本构模型

泥石流模型采用宾汉流体模型。已有研究表明对于较高浓度的泥沙悬浮液，其流变关系服从宾汉流体特性[7]，该模型认为动量是在固体颗粒之间的摩擦碰撞、液相泥浆之间的黏滞力传递的，用宾汉极限剪切应力和黏滞系数来表现颗粒之间的相互作用力，主要突出了泥石流中液相浆体的作用，而忽略其中大颗粒之间的相互碰撞作用对阻力的影响，因此模型适用于以细颗粒为主的黏性泥石流。其流变方程如下：

(1)

式中：τ为泥石流的剪应力，Pa；τB为宾汉体极限剪应力，Pa；μ为黏滞系数，N·s/m2；du/dy为剪切速率，m/s。

有限体积法在泥石流流体性质模拟上具有精度高、收敛性好的特点，在研究中已经得到了大量的应用[8-11]。该方法常将泥石流假定为均质流体而较难凸显大块石的撞击作用，因此本次研究通过有限元接触理论反演了泥石流中大块石的冲击作用，相较常规模拟研究更符合泥石流的冲击特性。由于石块撞击桥墩是一个瞬态的过程，块石材料在撞击过程中处于弹性变形范围内，因此石块本构模型采用线弹性模型进行简化计算。

1.2 桥墩材料本构模型

1.2.1混凝土模型

目前常用的混凝土本构模型有HJC、RHT、LLNL、Malvar和TCK模型[12]。本文采用RHT模型模拟混凝土非线性特性及损伤过程[13-15]，该模型广泛应用于模拟脆性材料的动态受荷过程，如岩石、混凝土和陶瓷冲击过程等。RHT本构模型是一种塑性和剪切损伤的组合模型，其材料中的偏应力受到广义破坏面的限制，其失效面主要表现为弹性极限面、失效极限面和残余强度极限面(见图3)，各极限面可以表达为初始屈服强度、峰值屈服强度和峰后残余强度。RHT本构方程将压缩阶段分为3个阶段：线弹性阶段、塑性过渡阶段、完全密实材料阶段。其中塑性压缩阶段采用多孔材料状态方程P-ɑ模型[16]，密实阶段采用描述密实材料的多项式状态方程。

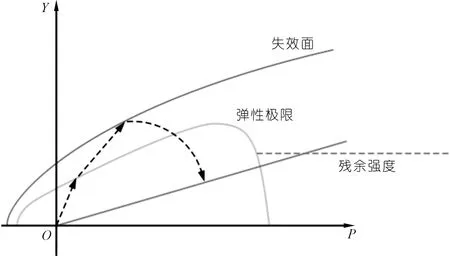
图3 RHT模型极限面压缩子午线

1.2.2钢筋模型

钢筋模型采用双线性各向同性弹塑性硬化模型，该模型可用于大变形分析。应力应变曲线如图4所示。曲线的初始斜率为材料弹性模量E，第二阶段斜率为正切弹性模量Et。因此定义钢筋模型时只需输入钢筋屈服强度σ0、初始弹性模量E和正切弹性模量Et，正切弹性模量不能大于初始弹性模量。

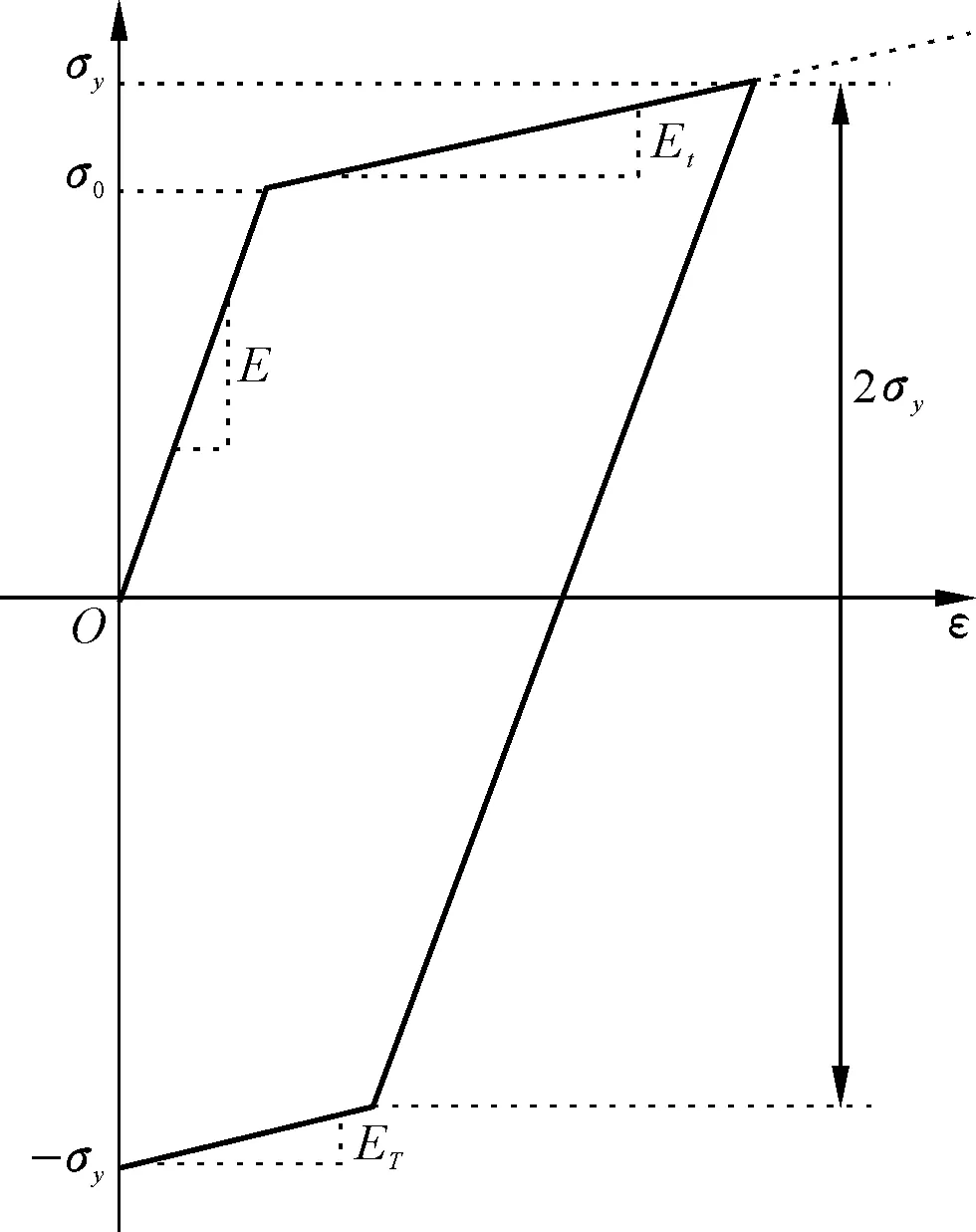
图4 双线性弹塑性硬化模型

1.3 计算过程及参数设定

流体模拟基于CFX有限体积法，泥浆模型采用VOF二相流(空气和泥浆)。本文认为当单元泥浆体积占比达到50%时，单元被泥浆占有，该单元速度等属性为泥浆属性。流体黏性模型采用k-ε模型，泥浆材料本构为宾汉体模型，动力黏滞系数为0.7 Pa·s，屈服应力为16 Pa，密度为1 750 kg/m3。由于泥石流冲击力主要集中于龙头上，因此冲击过程与时间有关，需采用瞬态分析，时间步长为0.005 s，计算500步即2.5 s。在初始化计算中，流体域和空气域均填充为空气，泥石流入口速度为10 m/s，上方空气入口为压力入口并设置压力差为0，出口均为压力出口，空气域上方为连通开口，压力为1个大气压。

基于有限元方法开展结构分析，泥石流的冲击作用在本次研究中等效为泥浆冲击荷载加大石块冲击作用。泥浆冲击荷载是CFX流体计算中桥墩边界位置压力；而大石块冲击作用则基于接触理论得到，石块的初始速度为10 m/s。桥梁上部结构传递至桥墩的顶端压力为4 500 kN，桥墩基础为固定端支座。在进行泥石流冲击作用前，先进行约0.5 s的静力荷载预加载，待桥墩完全稳定后再进行泥浆冲击，冲击时间约1.5 s时石块开始以10 m/s的速度冲向桥墩(预模拟中显示泥浆龙头接触桥墩到完全稳定约1.5 s)。

2 流场及结构动力特征

2.1 流场动力过程

泥浆流动过程可通过检测自由表面直观表示(见图5)。约在0.3 s时泥石流接触前墩并沿着桥墩绕流，相较于清水，泥石流具有较大的黏度，因此桥墩后方产生较为明显的空隙，被分流的泥浆于后墩汇合；随着泥石流接触后墩，两桥墩之间的空隙逐渐消失，约在1.7 s形成稳定的绕流流场。

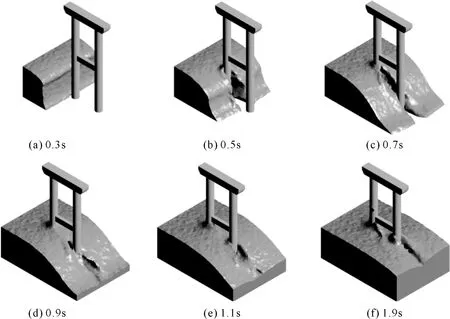
图5 典型时刻泥石流分布

2.2 流速分布

流速是泥石流动力过程研究的重要动力指标，也是泥石流防治工程中不可或缺的计算指标[7]。本文选取泥石流流域2 m高度的参考平面，通过输出该平面的速度来研究泥石流在运动过程中的流速分布规律(见图6)。泥石流在冲击前墩时产生较为显著的圆柱绕流现象，其特征是冲击方向的墩前和墩后速度趋近于0，桥墩两侧流速较初始速度显著增加，这与圆周绕流理论中流速分布一致。当流体冲击到后墩时也产生绕流现象，但稳定的后墩区域最大流速显然低于前墩流速。对流域内流速求最值以获取最大流速时程分布图(见图7)，泥石流冲击桥墩过程中的最大流速为双峰曲线，泥石流在接触前墩过程中流速迅速增加至顶峰，随后流速迅速下降，当泥石流接触后墩时流速轻微增加。因此流速波峰分别为前墩和后墩的冲击时刻，冲击前墩时流域平面最大流速为0.36 s时的21.3 m/s，而冲击后墩时平面最大流速为0.69 s时的16.8 m/s。

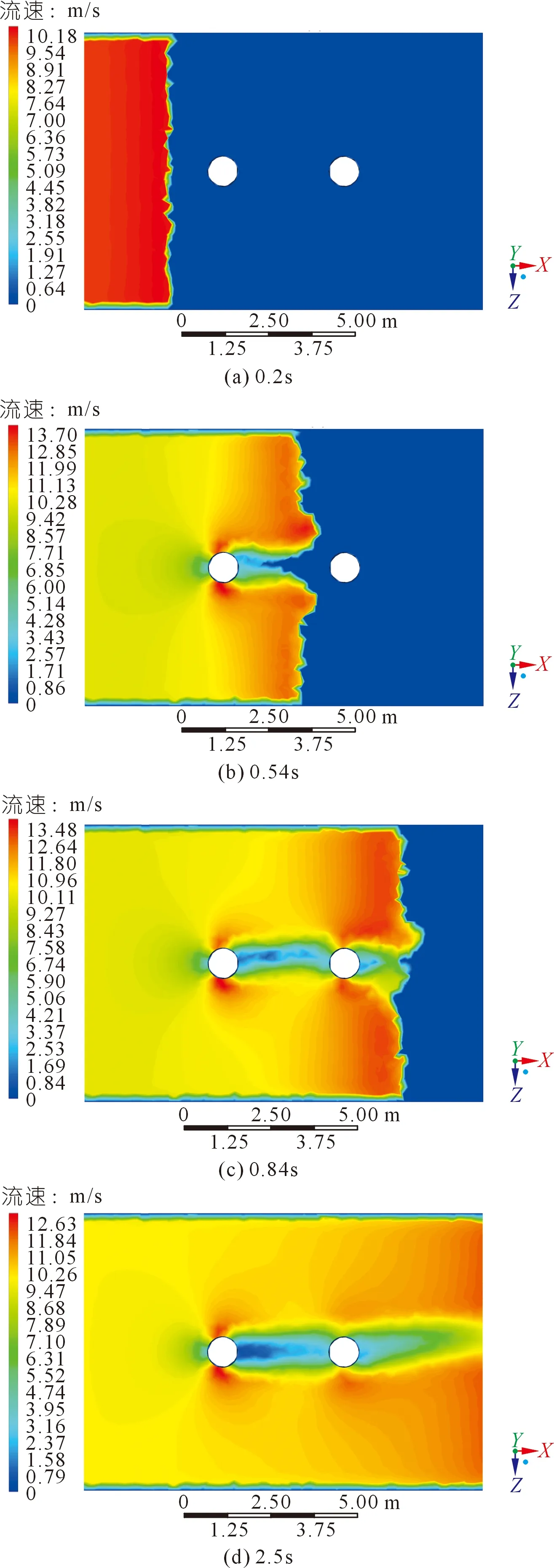
图6 典型时刻泥石流速度分布

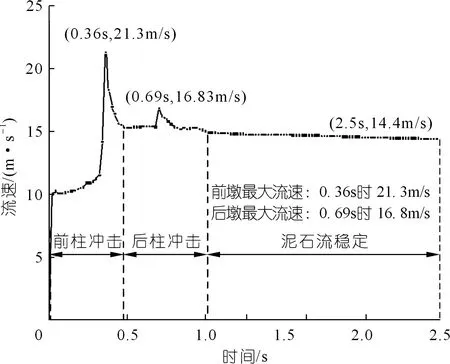
图7 平面最大流速时程分布

为探究速度突变的原因，分别导出速度波峰时刻的涡量云图(见图8)。观察两次最大速度突变时刻流域平面涡量，泥石流接触前墩时在桥墩前方产生了最大为5.58/s的正涡，而泥石流接触后墩时刻产生96.09/s的正涡和-115.71/s的负涡，因此泥石流接触桥墩时速度发生突增。

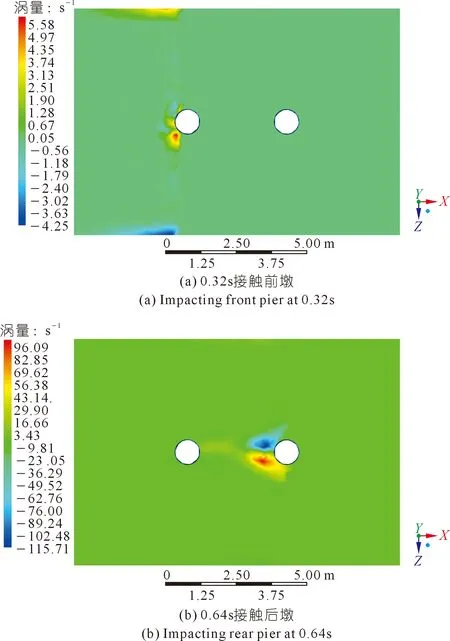
图8 涡量平面分布

2.3 冲击压力

2.3.1桥墩冲击压力分布

泥石流对桥墩的冲击压力可通过输出桥墩位置压力边界得到，前墩压力分布如图9所示，后墩压力分布如图10所示。

泥石流冲击前墩过程中，冲击压力在接触过程中呈三角形向外扩散(图9中0.28～0.32 s)，前柱冲击压力基底最大并沿高度逐渐减小。随着流体与桥墩的完全接触，流体将在桥墩上产生涌高，涌高流体的冲击压强上端仍符合三角形传播。当流体完全稳定后(见图9(f))，桥墩的压力分布相较于之前呈现下降。

图9 前柱桥墩冲击压力时程分布(单位：Pa)

泥石流绕流前墩并于0.56 s接触后墩，通过压力云图可以看出后墩左下角率先产生冲击压力，0.6 s时流体接触桥墩右侧并产生小于左侧的冲击压强，最大冲击压强并非位于桥墩基底而是位于桥墩高约0.5 m位置，显然是由于前墩的阻挡影响了后桥墩的压力分布。随着冲击时间增加，桥墩所受泥石流冲击压强呈现三角形点状分布并向四周扩散(见图10(d)和(e))。而当流体稳定时，桥墩的冲击压强呈右下角最大，左上和右上均较小。

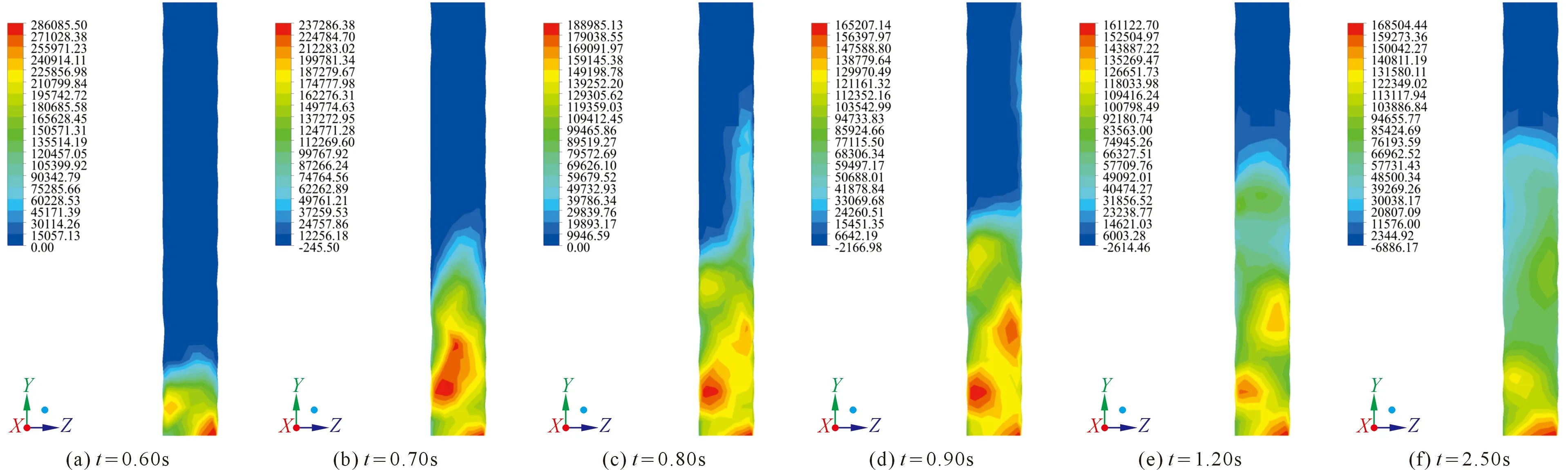
图10 后柱桥墩冲击压力时程分布(单位：Pa)

2.3.2冲击压力沿高度分布

为探究桥墩冲击压强沿高度变化情况，本文取前柱表面和后柱表面的中线作为参考线，以桥墩高度位置为x轴，冲击压强为y轴建立典型时刻下桥墩压强沿高度分布曲线(见图11和图12)。

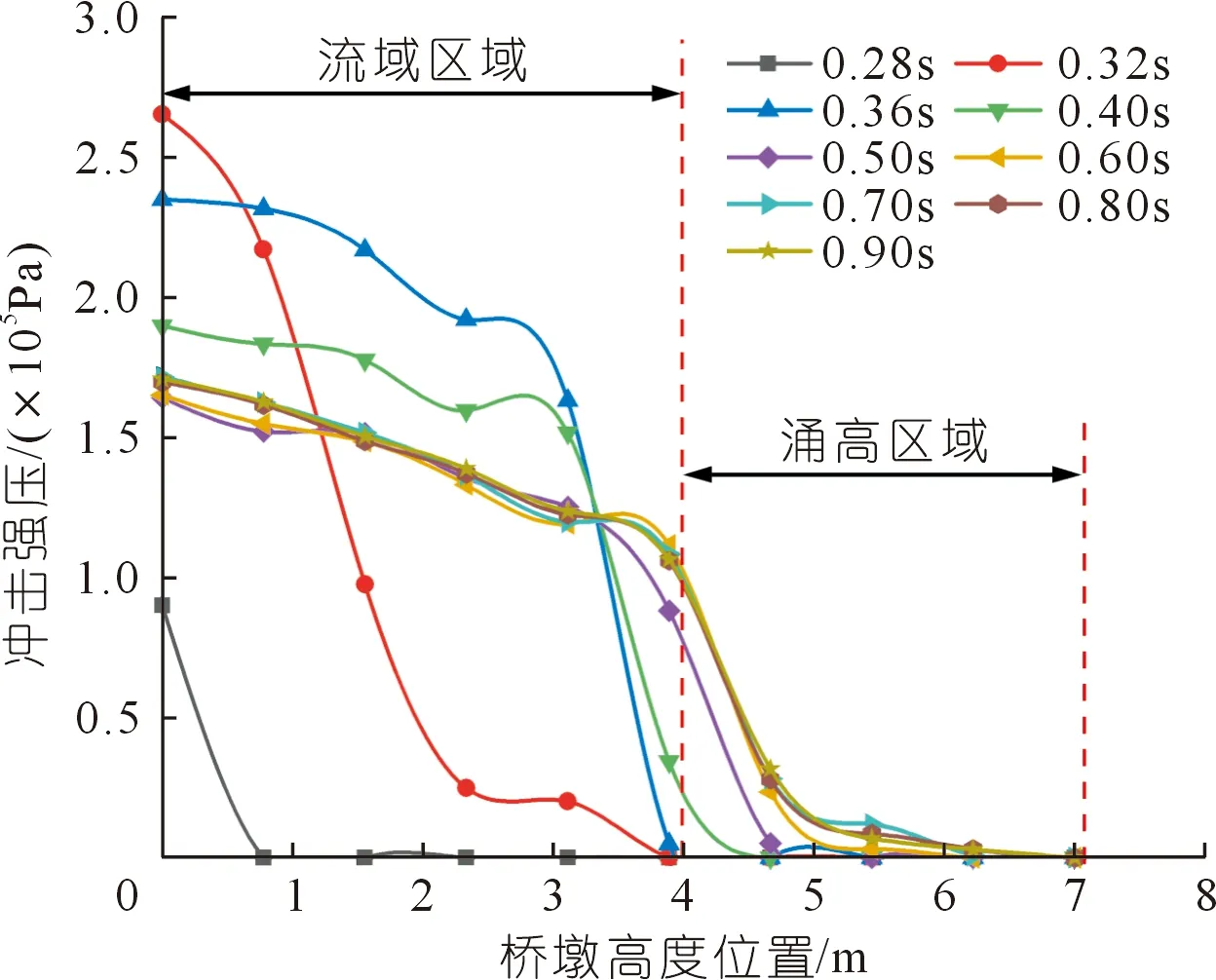
图11 典型时刻前墩不同高度冲击压强

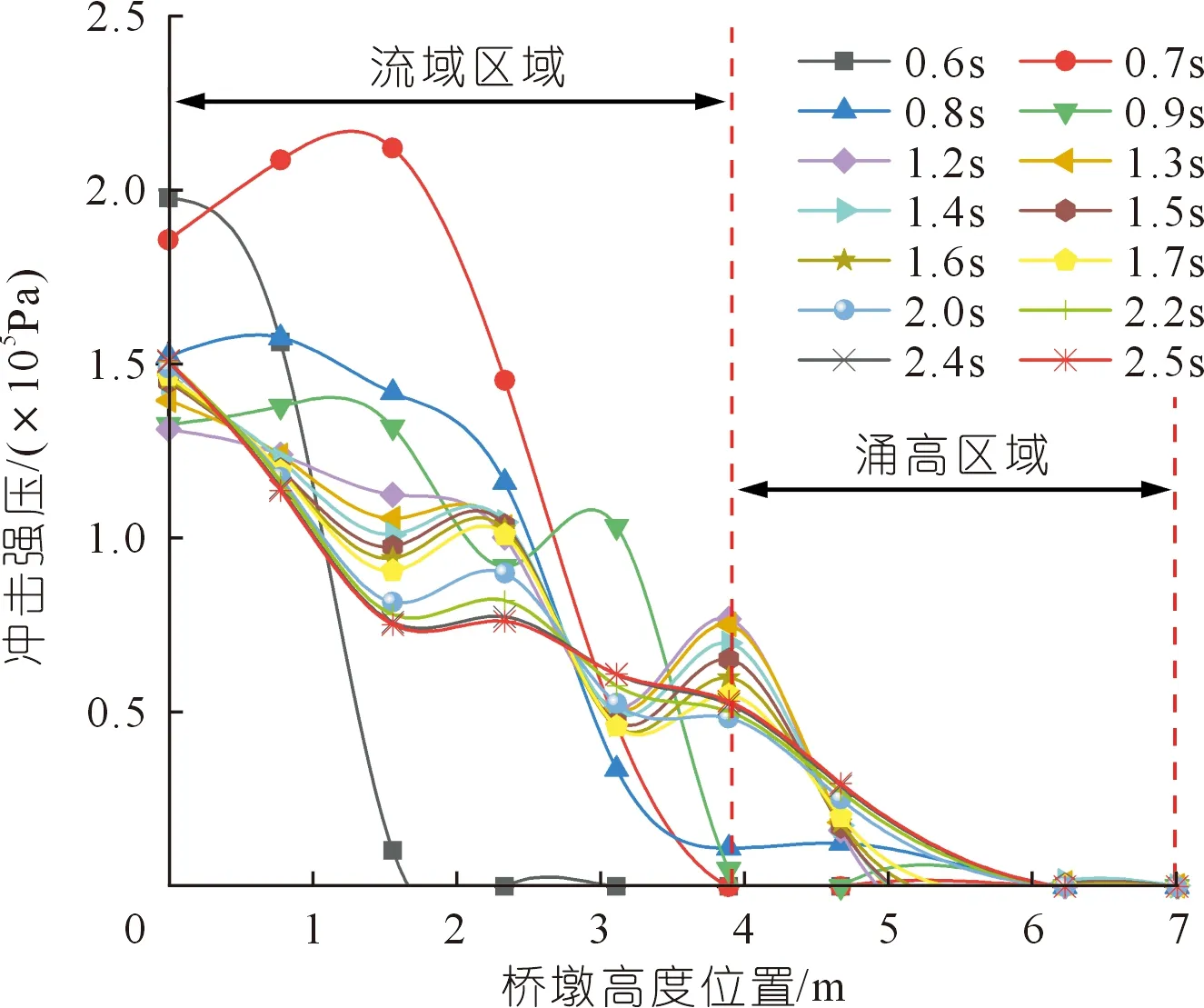
图12 典型时刻后墩不同高度冲击压强

前柱桥墩冲击过程中流体压强变化总体趋势为：① 在时间尺度上，泥石流刚接触桥墩时为最大冲击压强时刻，随着冲击时间增加流体逐渐稳定，最大冲击压强逐渐降低并趋至稳定。② 稳定后泥石流流体沿着桥墩高度呈现两段式衰减：稳定流体衰减和涌高流体衰减，稳定流体高度处压强衰减幅度远小于涌高流体压强衰减幅度。

后柱桥墩冲击压强沿着高度方向呈现较为显著的时间顺序(见图12)，0.6～1.2 s为泥石流冲击后柱桥墩初始阶段，0.6 s时泥石流冲击压强沿着高度方向迅速减小，约0.7 s时冲击压强产生峰值，峰值位置约为1.2 m高度。1.2 s后流体逐渐稳定，冲击压强在高度方向上呈现双峰曲线，由1.2 s后柱压力云图(见图13)可知桥墩压力分布为三角形分布，其波峰分别位于2.2 m和3.8 m位置。随着冲击时间的增加，压强曲线的波峰波谷逐渐减小，当泥石流完全稳定时(2.4 s，2.5 s)，压力的波峰波谷趋于平缓，并最终沿着高度方向稳步下降形成一条单调递减的压力曲线。

图13 1.2 s时后柱冲击压强分布

2.3.3冲击力时程趋势

为分析桥墩冲击压力时程分布，分别导出桥墩最大压强时程曲线(见图14)和冲击力合力时程曲线(见图15)，其中桥墩最大压强时程为某一时刻下桥墩表面冲击压强极值，而桥墩冲击力合力则是通过单元面积乘以单元压强再进行矢量求和得到。

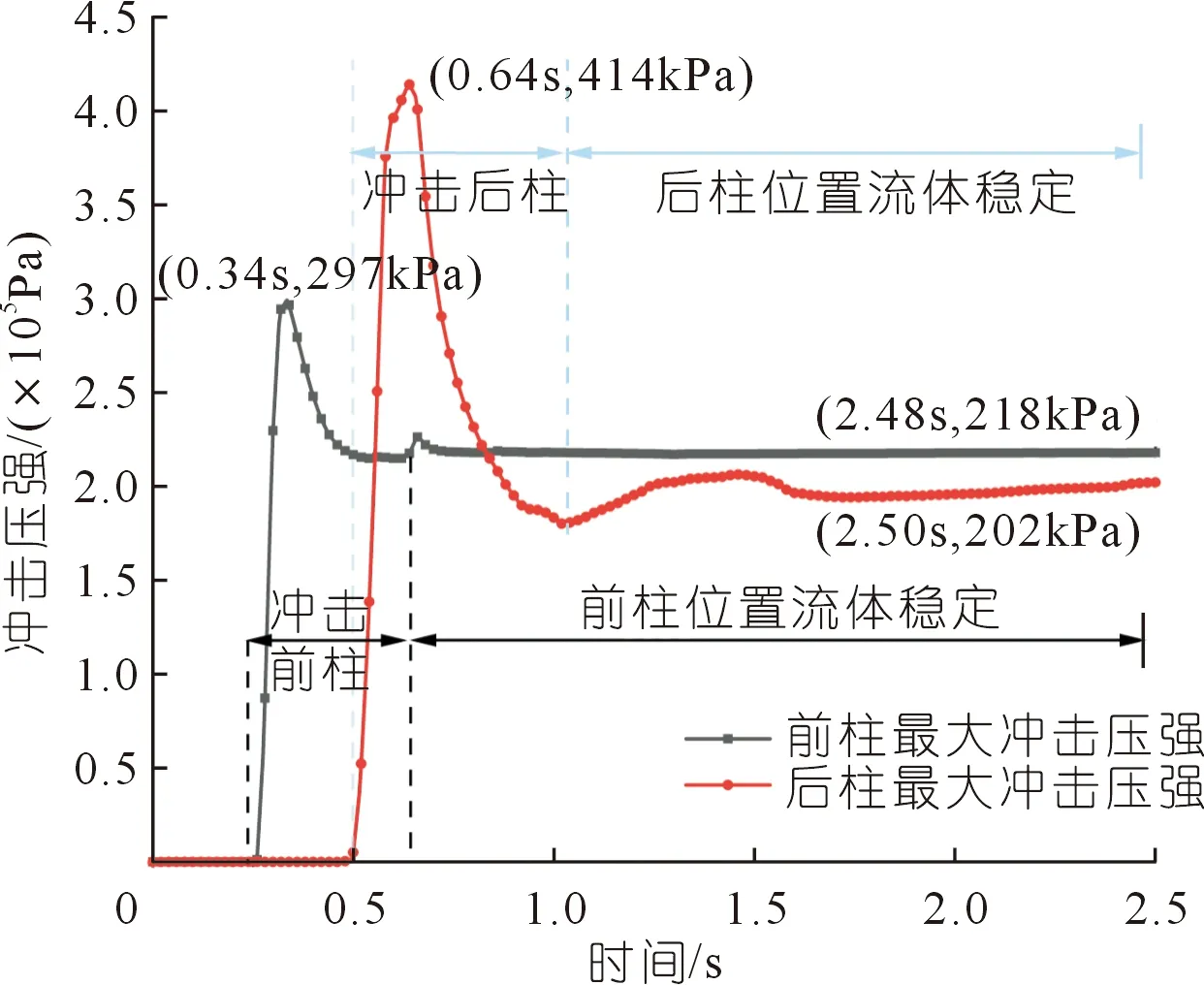
图14 最大冲击压强时程

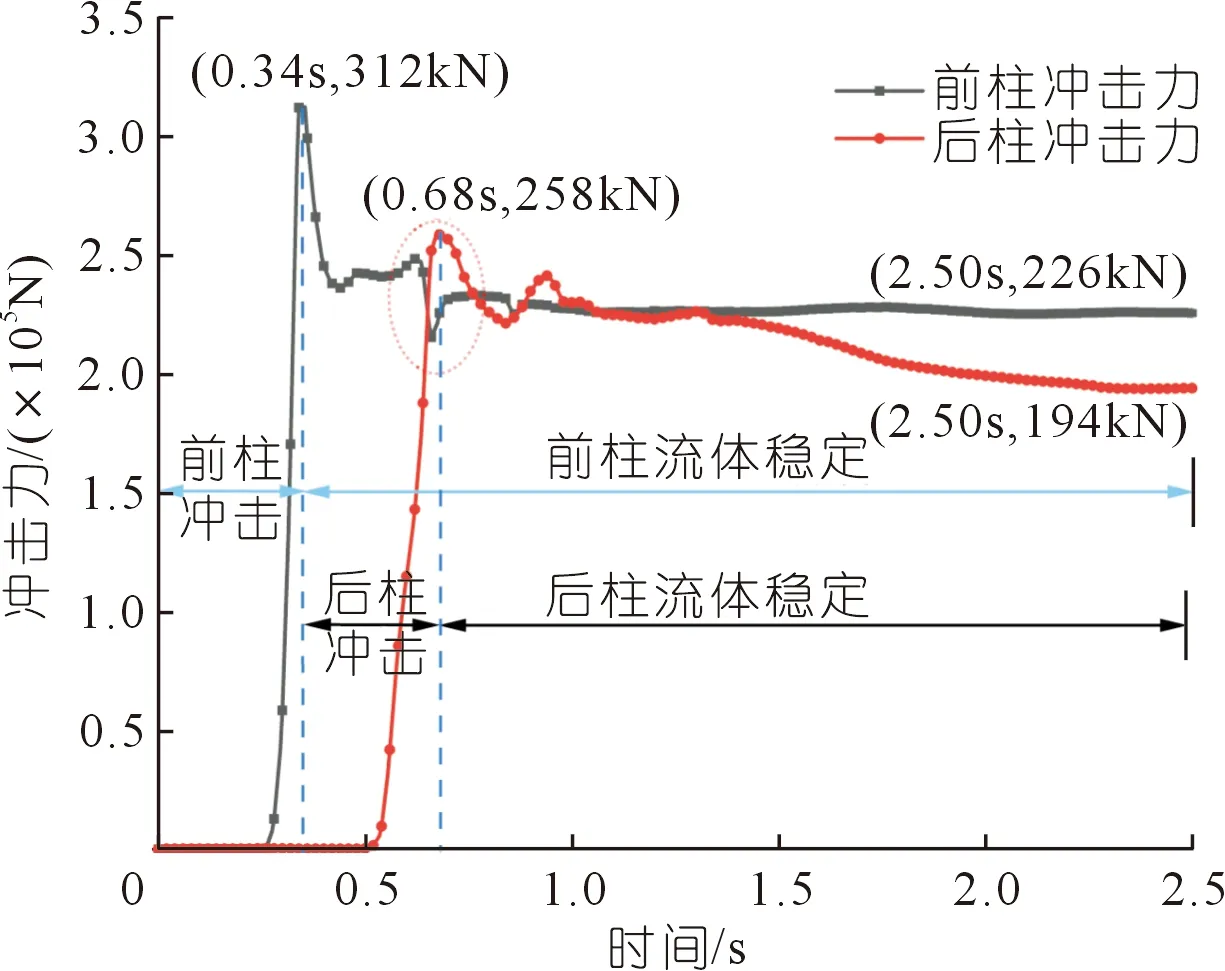
图15 桥墩冲击力时程

依据桥墩最大冲击压强时程曲线(见图14)，前柱冲击压力峰值为0.34 s时的297 kPa，后柱冲击压力峰值为0.64 s时的414 kPa；流体稳定后泥石流对前柱产生的持续冲击压强为218 kPa，对后柱产生的冲击压强为202 kPa。当泥石流冲击桥墩时后柱较前柱的峰值冲击压力增加了约48%，前柱稳定冲击压力较于后柱增加了约8%。峰值压力方面前柱远小于后柱，而对于稳定冲击压强前柱则略大于后柱。通过曲线可以反映泥石流冲击桥墩过程中最大冲击压强的规律如下：泥石流接触桥墩时产生最大压强快速攀升至顶峰，随后绕流运动使得最大压强下降，冲击压强随着流体的稳定趋于稳定。对比前后柱体可知后柱的瞬时最大压强大于前柱瞬时最大压强，但流体稳定后的后柱冲击压强则小于前柱。

依据泥石流对桥墩的冲击力合力时程(见图15)。泥石流对前柱桥墩产生的冲击力峰值为0.34 s时的321 kN，对后墩产生最大冲击力为0.68 s时的258 kN。泥石流稳定后对前柱的持续冲击力为226 kN而对后柱的持续冲击力为194 kN。当泥石流冲击桥墩时前柱较后柱的峰值冲击力增加了约24%，前柱稳定冲击力值较于后柱稳定值增加了约16%。通过对比最大冲击压强时程(见图14)和桥墩冲击力时程图(见图15)，桥墩峰值压力和峰值合力所对应的时刻基本一致，均出现在泥石流冲击龙头位置。前柱峰值压强远小于后柱，但前柱峰值冲击力却大于后柱峰值冲击力，证明泥石流在冲击桥墩过程中后柱产生了局部极大压强。

2.4 桥墩动力响应

2.4.1桥墩应力分布

桥墩应力(见图16～17)能反映桥墩混凝土破坏特征及应力传播特征。在泥浆冲击桥墩1.5 s后，石块与桥墩在2.06 s接触，接触位置受石块作用产生正压力，接触表面内外均产生最大应力，并自撞击点呈圆形向四周扩散，除接触位置产生最大应力外，桥墩底端产生较大应力。随着应力的扩散，在石块接触桥墩时，桥墩基底位置和横梁位置等处于形状突变位置产生应力集中现象。随着撞击过程的稳定，石块产生的冲击力导致桥墩的晃动，此阶段应力主要集中于桥墩基础的前后端、系梁与桥墩接触的位置以及上端盖梁和墩体连接的位置(见图17)，此阶段的应力是由于桥墩自身的晃动导致的。

图16 2.06 s时石块接触桥墩应力分布(单位：Pa)

图17 2.30 s时桥墩振动应力分布(单位：Pa)

对于泥石流冲击桥墩的剪应力分布过程(见图18)，石块接触前柱时桥墩剪应力主要集中于基底和墩体两侧，而随着桥墩冲击的进一步稳定，桥墩剪应力则集中于基底、柱间系梁两侧、桥墩与承台的交接面。因此通过剪切应力云图易知，泥石流在冲击桥墩过程中，桥墩底端、系梁、桥墩与承台的接触面容易发生剪切破坏。

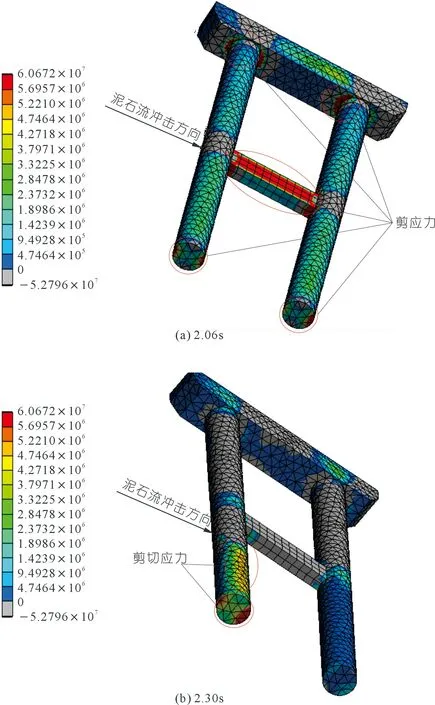
图18 桥墩剪切应力云图(单位：Pa)

2.4.2桥墩形变规律

为了观测桥墩损坏过程，可获取石块撞击桥墩时刻和桥墩振动过程中某一时刻下的应变云图(见图19)。混凝土极限应变为0.002，因此对应变云图进行分级，图中红色表示已经破坏的混凝土区域。石块在接触桥墩的过程中，混凝土应变率先到达极限状态的区域是石块撞击点、桥墩基础位置以及系梁连接位置，这些位置由于应力集中率先被破坏掉(见图19(a))。随着石块接触消失，桥墩在冲击荷载作用下发生晃动(见图19(b))，此时刻下桥墩应到极限应变位置主要集中于系梁4个边角处和桥墩基础。因此综合应变分析结果可知桥墩在泥石流作用下损坏位置主要为冲击点、桥梁基础和系梁位置。

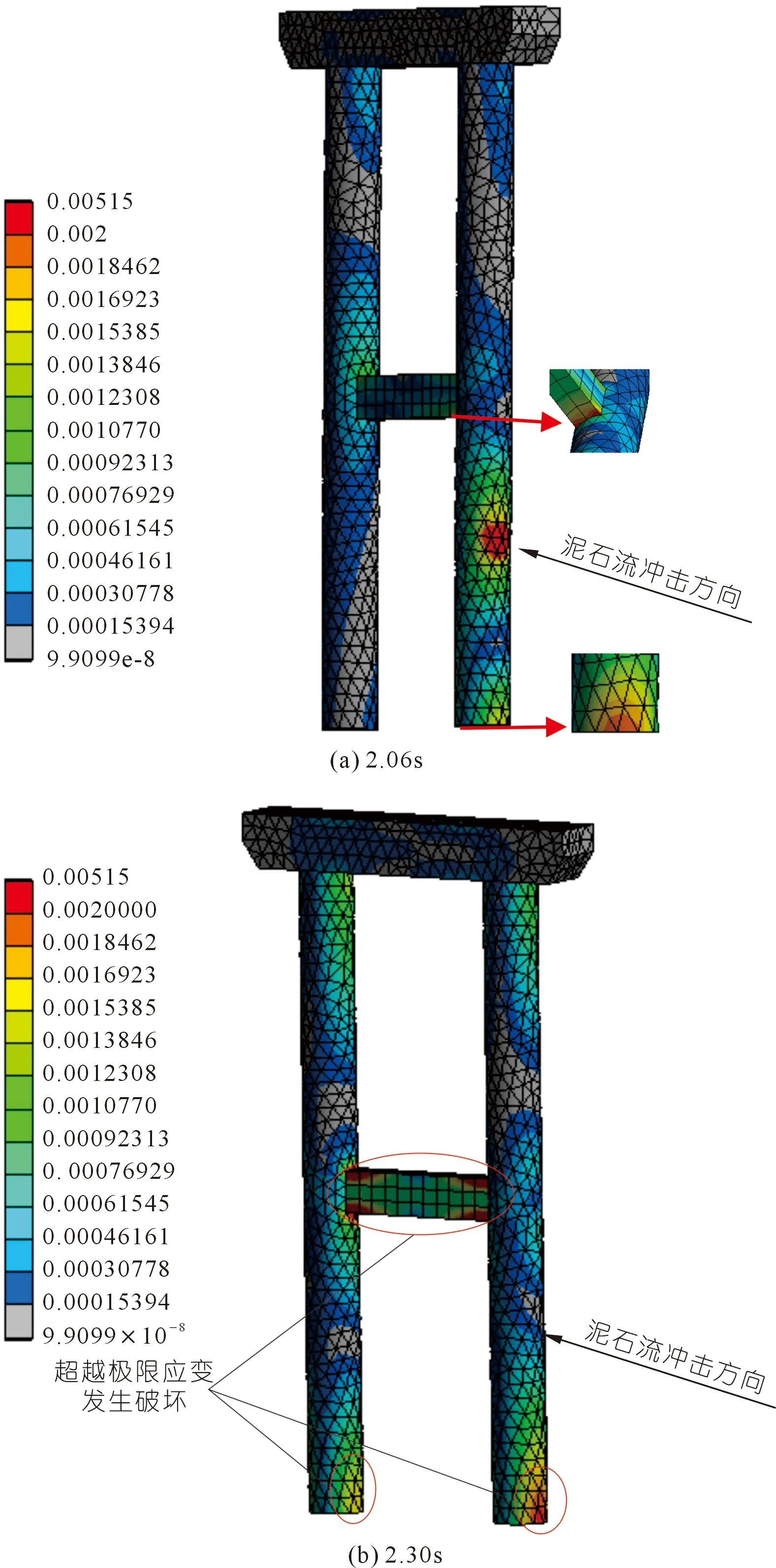
图19 桥墩应变云图

泥石流对桥墩的作用不仅对桥墩本身造成破坏，也会通过桥墩盖梁传递至上部结构，因此桥墩顶端位移可间接反映出泥石流对桥梁上部结构功能的影响。桥墩盖梁中心点位移时程如图20所示。桥墩受力加载的3个阶段具有不同的3段位移。0～0.4 s为静力加载过程，此阶段产生的位移为上部梁盖荷载及桥墩自身重力产生的竖向位移，位移曲线为缓步上升的直线，该阶段产生的压缩位移为2.2 mm。第二阶段为浆体冲击阶段，时间为0.4 s～2.0 s，浆体冲击导致桥墩发生振动并产生细微的横向位移，此阶段由于浆体的作用力很小，因此桥墩振动时振幅较小，桥墩的横向位移也较为细微，所以该阶段的位移曲线为缓步上升的正弦曲线，泥浆冲击阶段导致桥墩发生位移为4.4 mm。第三阶段泥石流中的大石块接触桥墩并产生较大的振动和位移，石块接触桥墩瞬间(约0.12 s内)桥墩顶端达到位移峰值约8.03 cm，随后桥墩发生大幅度振动，随着时间的增加由于自身阻尼存在其振动幅值随着时间逐渐衰减，通过位移不难发现该阶段产生的位移较大、振动明显，容易导致桥梁上部结构因超过位移限值和振动幅度而发生结构破坏。

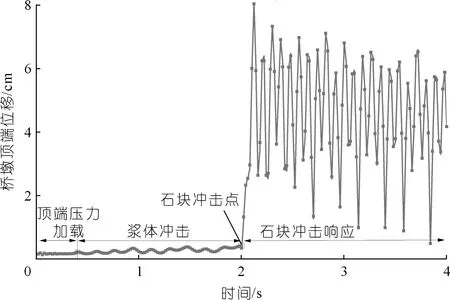
图20 桥墩顶端位移

2.4.3基底反力及弯矩

泥石流作用下对桥墩的基底反力及弯矩开展分析有助于在桥墩的基础设计中考虑灾害作用效力。基底反力时程如图21所示。在静力加载阶段，桥墩只受顶端荷载及自重作用5 000 kN，基底反力合力等于y方向基底反力，并由于桥墩的微量变形导致基底反力出现波动。在泥浆冲击阶段，在冲击方向(x方向)产生了较为轻微的冲击力，约445 kN，桥墩产生轻微振动使得反力时程为持续性的抖动波，此阶段基底反力合力基本等于桥墩荷载。当石块接触桥墩时，基底反力峰值为6 977 kN并产生了持续性振动。桥墩弯矩反力与基底反力时程基本一致，在泥浆冲击阶段基底开始出现弯矩，石块的冲击作用导致了基底弯矩瞬间增大，并随着桥墩的振动产生波动的正负弯矩，桥墩基底弯矩主要由冲击方向(x方向)合力导致的，而静荷载导致的基底弯矩y基本为0。

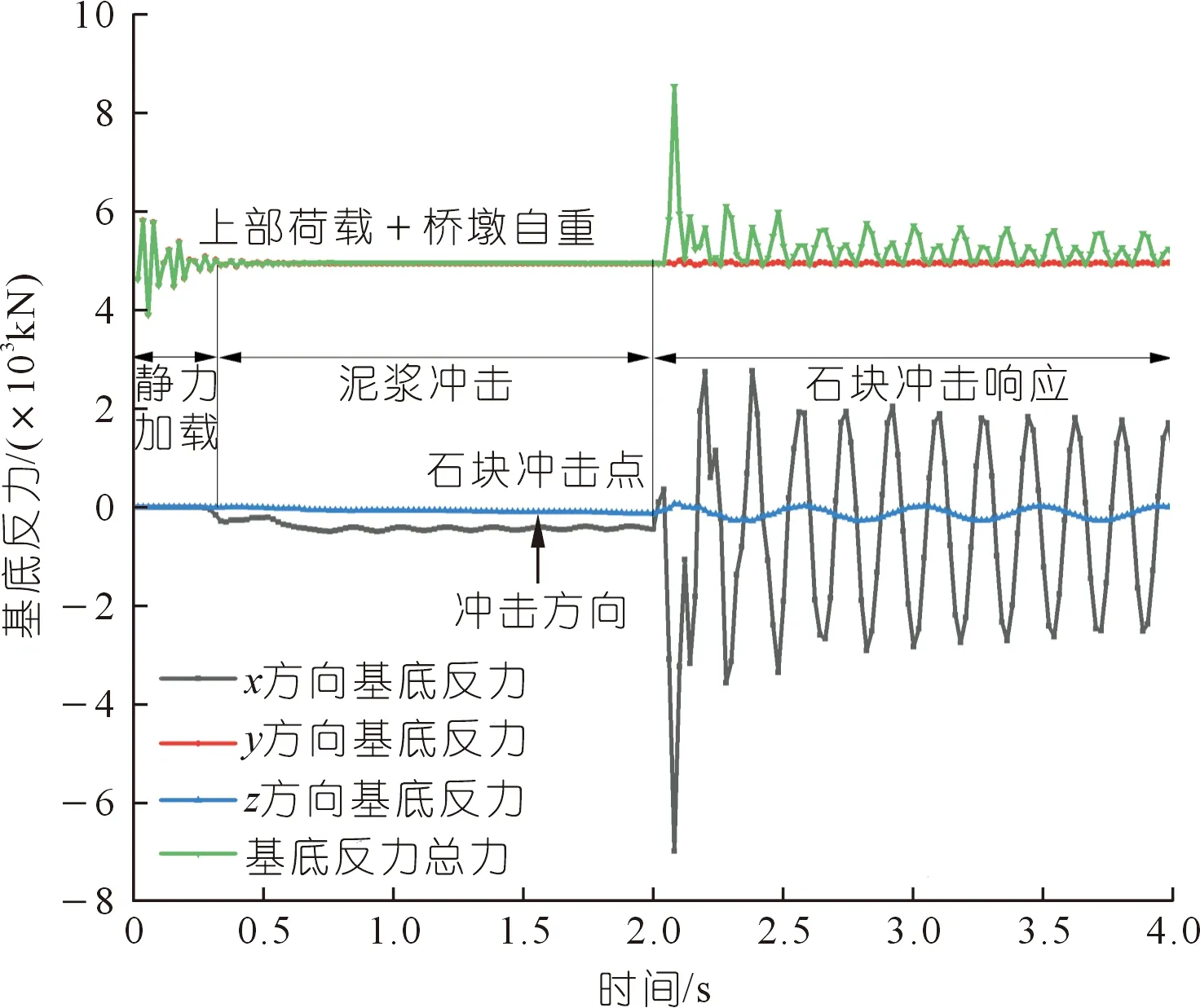
图21 基底反力

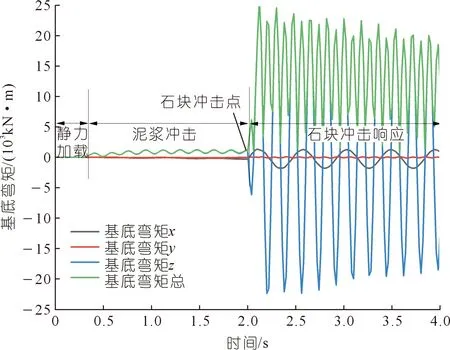
图22 基底弯矩

3 模拟验证

3.1 动压力系数验证

通过泥石流冲击桥墩过程中浆体压强分布获取峰值动压强，根据浆体动压力[17]公式(2)反算动压力系数，再对比相关学者的动压力系数进行论证。泥石流在冲击桥墩过程中前柱产生的浆体动压力峰值为297 kPa，泥石流接触桥墩时速度为13.5 m/s，如表1所列。

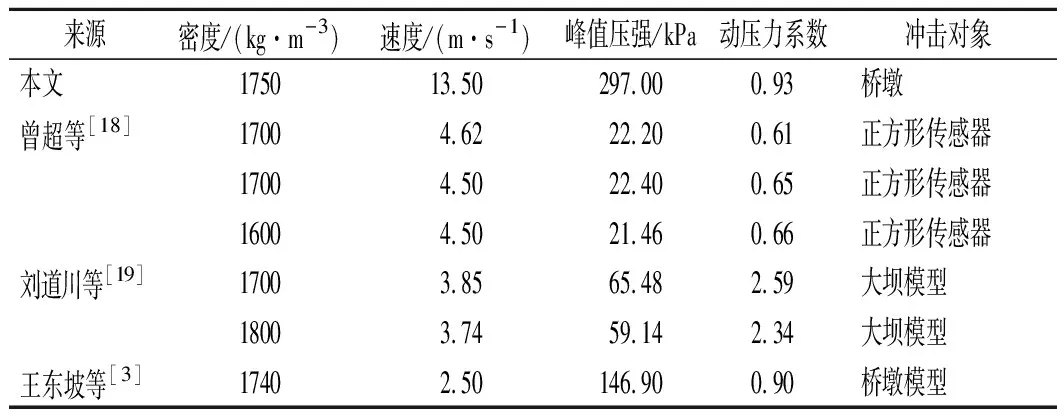
表1 泥浆动压力冲击力对比

P=α·ρ·v2

(2)

式中：ρ为浆体密度，kg/m3；v为浆体速度，m/s。

表1中曾超等[18]为获取泥石流压力时程特征，开展了泥石流冲击正方形传感器的小尺度试验，数据获得的动压力系数约0.65；刘道川等[19]开展了泥石流冲击刚性坝试验，所测得的动压力系数约2.4左右；王东坡等[3]开展的泥浆冲击桥墩模型试验所计算的动压力系数约为0.90。综合上述研究，刘道川等开展的试验中传感器放置在长方形容器中，因此泥石流冲击挡板后会停滞于挡板前并不会发生流动，此时测得的压力包含有浆体静压力，计算所得的浆体动压力系数是偏大的。曾超等开展的冲击试验所配置的泥浆较稀，模型的比率也对动压力系数有一定影响，测得的浆体动压力偏小。王东坡等开展的大比例尺试验，冲击对象为桥墩模型，与本文获取的动压力系数较为接近。

3.2 泥石流总压力验证

泥石流冲击桥墩可看作圆柱绕流现象，因此可参照流体力学阻力计算公式计算泥石流对桥墩的冲击合力如公式3。T/CAGHP006-2018《泥石流灾害防治工程勘查规范》[20]认为当被冲击形状为圆形时Cd为2，王友彪[21]认为该取值尚未考虑泥石流本身性质，太过保守，因此基于试验对其进行修正，认为稀性取值为0.9，黏性取值为2.3。

(3)

式中：Cd为冲击合力系数；H为泥石流来流流度，m；D为桥墩迎流面宽度，m。

依据王友彪修正的泥石流整体冲击力计算公式计算得整体冲击力为283.5 kN，采用规范计算得到桥墩整体冲击力为630 kN，本文所得泥浆冲击前柱过程中所产生的冲击力峰值为312 kN(见图15)。规范所计算的整体冲击力考虑了大块石的的冲击力，因此冲击结果远大于本文和王友彪的研究结果。而本文与王友彪在浆体冲击力上由于未考虑大块石的作用，因此计算结果较为接近。

3.3 石块冲击力验证

石块冲击力可采用牛顿第二定律计算，石块撞击桥墩时的最大冲击力可等价为石块质量乘以最大加速度。大石块质量为12 566 kg，由石块加速度时程知撞击过程中最大加速度为502 m/s2，因此采用牛顿第二定律计算得到的冲击力为4 728.8 kN。

现有大石块冲击力的计算公式主要基于弹性球体假设建立[22-24]，对比各学者冲击计算公式计算得到的大石块冲击力发现，大石块产生的冲击力略低于Yamaguchi[22]和水山高[23]研究成果，略高于Huang等[24]计算的冲击力。

表2 石块冲击力结果对比

3.4 试验对比

顾乡[25]开展了落石冲击桥墩试验。该试验将桥墩模型两端固定让自由落体的铁块冲击桥墩表面，进而获取桥墩的损坏状态。根据模拟中冲击点应变云图和试验桥墩损伤对比，模拟中桥墩临界应变集中于冲击点处，损伤形状为自撞击点处以圆形扩散(见图23(a))；试验中冲击点处混凝土被压碎，损伤近似于圆形(图23(b))，因此模拟和试验在损伤断面上较为吻合。

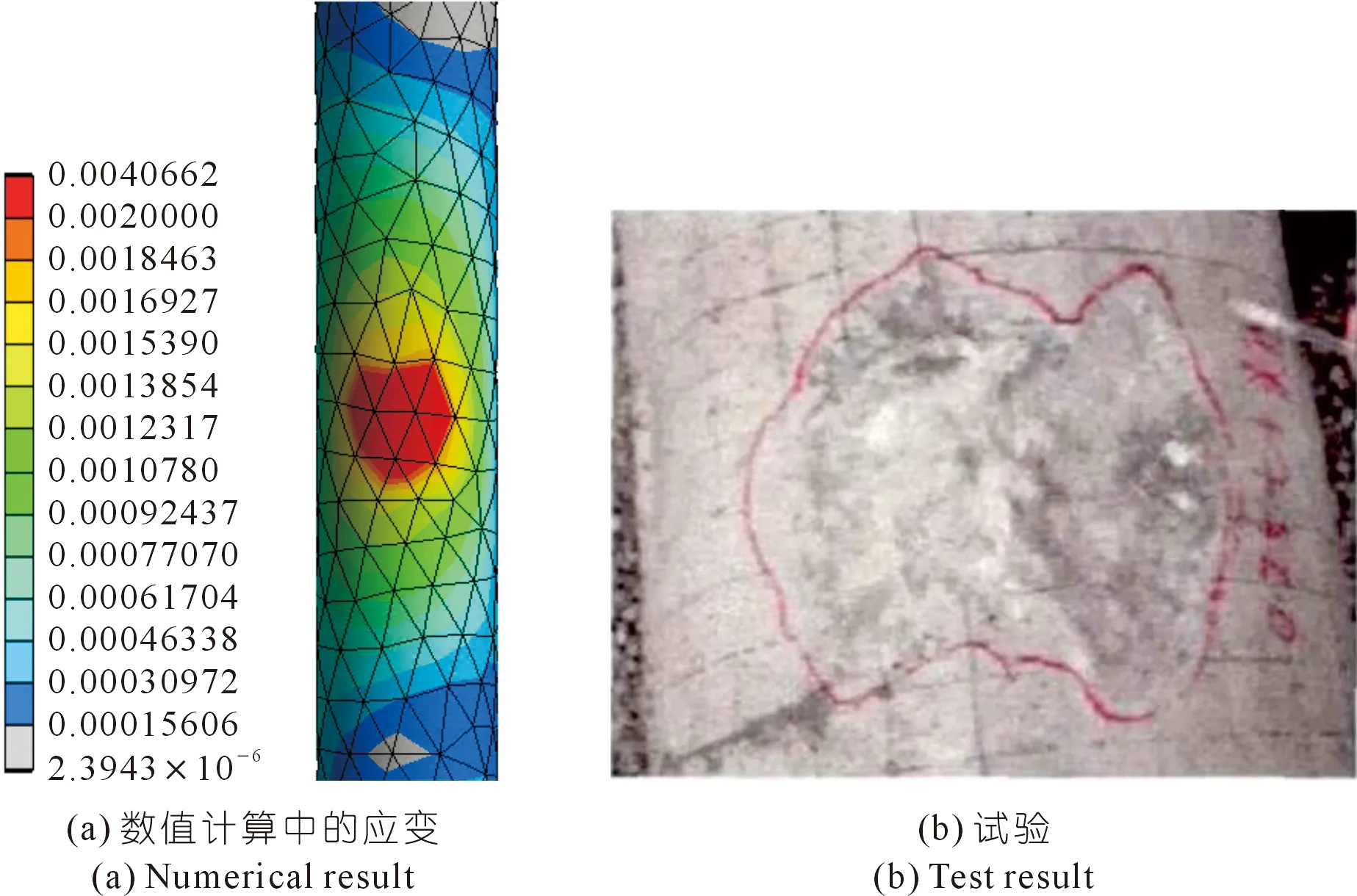
图23 落石冲击桥墩产生的损伤

数值模拟中桥墩挠度较为细微，因此对图像挠度放大10倍，如图24所示。图24(b)为试验条件下石块冲击桥墩产生的挠度变形。由于模拟过程涉及到流固耦合，故采用的为隐式求解器暂无法输出裂缝，但在模拟和试验中，桥墩的迎冲面向内凹陷冲击点背面向外凸出，挠度趋势符合实际。

图24 桥墩冲击时挠度

4 结 论

本文总结了泥石流作用下双柱桥墩动力响应过程及泥石流的分布规律，建立了双柱桥墩的三维有限元模型，通过有限元方法分析了结构应力响应和位移时程响应，并验证了模拟的准确性。主要结论有：

(1)泥石流在冲击双柱桥墩过程中产生了较为显著的圆柱绕流现象，其特征是冲击方向的墩前和墩后速度趋近于0，桥墩两侧流速较初始速度显著增加。

(2)泥石流对桥墩的冲击压力极值发生在泥石流接触前柱和接触后柱的时刻，前柱冲击压力自接触位置呈三角形向外扩散，后柱冲击压力呈三点式集中分布，前柱对后柱产生的遮蔽效应显著减小了泥石流对后柱的冲击力合力。

(3)桥墩基底、系梁、桥墩与承台的接触面剪切应力较为突出，易发生剪切破坏，而桥墩基底、系梁连接位置、石块冲击位置容易发生应力集中而率先发生破坏。

(4)浆体冲击导致桥墩产生细微的振动和横向位移，而石块的冲击容易产生大幅度振动和较大横向位移，威胁桥梁上部结构。