基于LMD-XGBoost和KPCA的燃气轮机转子故障预警研究

章明明,茅大钧,董渊博

（上海电力大学自动化工程学院，上海 200000）

0 引言

燃气轮机技术已在世界各国得到广泛研究和利用。据国家能源局统计，2021年中国天然气发电行业装机总量超过1.1亿kW，预计“十四五”期间天然气发电仍将快速增长，到2025年将新增4 000～5 000万kW发电机组。作为一种大型旋转动力设备，燃气轮机的内部结构复杂，在高温、高压和高转速的环境下长期运行，容易发生故障。其中转子作为燃气轮机整机的核心，其故障率占比最高，达45%以上。因此，在燃气轮机转子故障早期进行有效预警，及时发出报警信号，变事后维修为事前预防，对延长燃气轮机的使用寿命，提高电厂的经济效益具有重要的意义。

目前国内针对重型燃气轮机转子故障的研究主要集中于故障诊断，大多采用机理建模的方法研究转子动力学特性，贺雅等[1]通过机理分析研究燃气轮机转子不平衡故障，在研究多转子不平衡振动的响应关系和响应规律、激励的基础上，提出一种基于计算不平衡因子的燃气轮机不平衡部位识别方法，对燃气轮机多转子系统的动平衡有一定的指导意义；蒋龙陈等[4]使用非线性调频分量分解方法对燃气轮机机匣振动信号进行时频分析，并利用卷积神经网络对燃机转子进行故障诊断，且准确率较高。龚海鹏等[8]提出一种基于小波包和带有偏差单元的内部回归神经网络相结合的燃气轮机转子故障诊断方法，有效地提升了诊断效率和准确性。目前燃气轮机转子故障研究缺乏对海量历史数据的利用及对事前预警机制的研究，并且在已有的研究成果中依旧存在如下问题需要进一步分析和解决：

1）振动信号有效去噪。

2）振动趋势智能预测方法的优化。

3）故障预警模型的准确性验证。

针对以上问题，在前人研究基础上提出一种基于极端梯度提升和LMD-KPCA的燃气轮机转子故障预警方法，以机组个体的自身振动数据为监测对比对象，尝试进行转子早期故障的预警，并通过电厂实际运行数据验证其可行性。

1 转子故障预警算法研究

1.1 自适应小波阈值降噪

小波降噪算法的实质是通过去除高斯白噪声，抑制信号的噪声部分，恢复信号有用成分，一般分为3步：

1）信号的小波分解。选取合适的小波基函数，对信号进行指定层次的分解和计算。

2）阈值量化。小波分解得到不同分解尺度下的高频系数，选取合适阈值对其进行阈值量化处理。

3）信号重构。利用小波分解得到的低频系数和高频系数重构有用信号。

当前使用最多的两种阈值函数为硬阈值和软阈值，但存在信号缺乏光滑性，小波系数偏差大等问题。为了滤除噪声并且同时保留信号本身的奇异性，本文采用一种自适应阈值函数和最佳阈值对转子振动信号去噪。选用的自适应函数为：

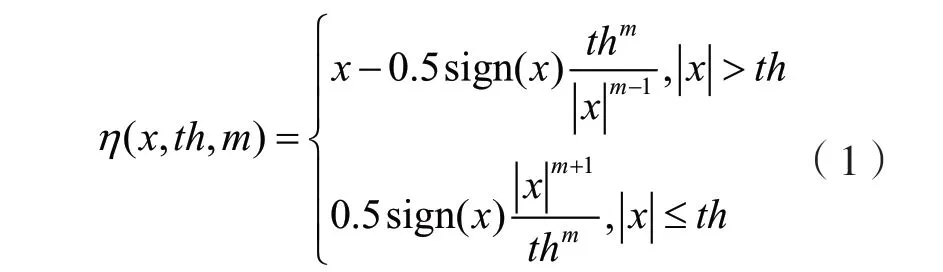
式中：th为阈值，通过求解极小值可获得对应尺度的最优阈值th；m为可调参数，可取大于1的连续实数，m决定了函数形状、性质，当m接近于1时，类似于软阈值函数，当m>1时，类似于硬阈值函数。

1.2 局部均值分解

局部均值分解（Local Mean Decomposition，LMD）是由Jonathan S.Smith学者提出的一种可自适应处理非平稳信号的新方法。对原始信号不断进行解调得到纯调频信号，在获得纯调频信号后再进行包络信号与纯调频信号相乘得到PF分量。组合PF分量相对应的瞬时幅值和瞬时频率，就能获得原始信号完整的时频分布。对于信号X(t)，分解流程如图1所示。

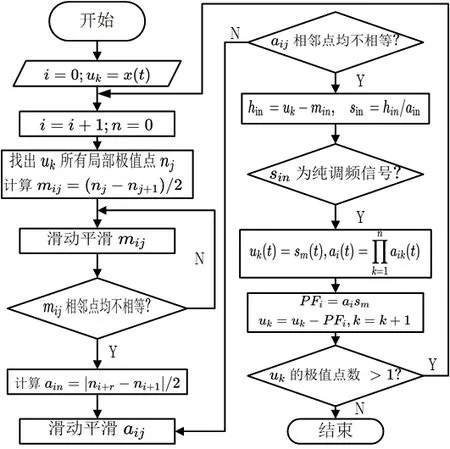
图1 LMD分解流程

1.3 极端梯度提升

XGBoost的核心是在保证回归树树群泛化能力的前提下，利用多个回归树来降低预测误差，类似最优化泛化函数。函数空间中的损失函数为：

等式的右边包括正则化项和误差函数两部分，整个模型的输出为误差函数中的参数。

正则化项表达式为：

式中：T为叶子节点个数；ω为节点数值；γ和λ为叶子和权重的惩罚项。

再对XGBoost的损失函数进行了二次泰勒展开可得：

对上式求导得ω*j=-，将结果代入原式，得到最终的目标函数为：

1.4 基于核主元分析的故障检测

利用KPCA进行故障监测的指标有两种，统计量T2和平方预测误差SPE。统计量T2可度量模型内部变化，通过变化趋势和幅值反映出每个主成分偏离模型的程度；SPE统计量可度量模型外部变化，表征测量值对主元模型的偏离程度。

假设存在一个信号矩阵X（m×n），载荷矩 阵P（n×r），主 元 矩 阵T（m×r），tj为m×1的向量，定义T2的统计量为主元得分，计算出主元得分值T，测量估计值及残差e，计算过程如下：

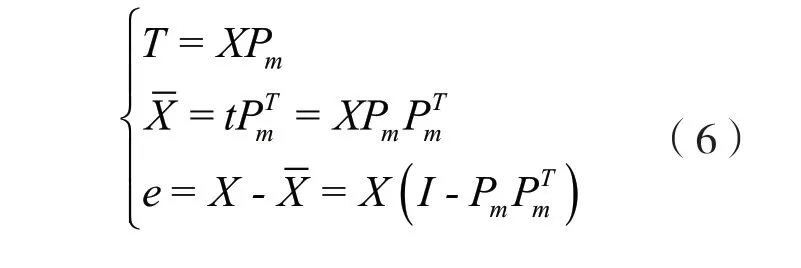
则主元统计值T2为：

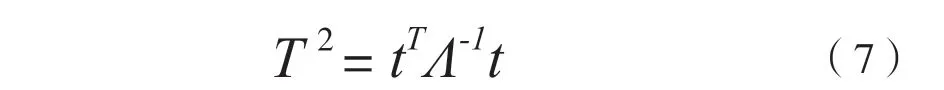
式中：Λ=diag（λ1，λ2，…）；m为主元个数；λi为协方差矩阵第i个特征值；T2的阈值服从自由度为m和n-m的F分布F（m，n-m），其中n为样本采样点数，设定a为显著性检验水平，则：

平方预测误差SPE衡量样本向量在残差空间的投影的变化，其计算公式为：

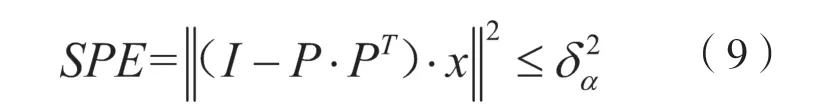
其中，δα2表示置信度为α的控制限。δα2的计算公式如下：

2 基于混合预测的转子故障预警模型

燃气轮机转子故障预警的整体思路如图2所示。

图2 预警整体思路

首先，对转子数据进行降噪处理。在保留信号奇异性的前提下，尽可能滤除噪声。

然后，利用LMD分解得到的特征分量，建立基于极端梯度提升的转子振动信号的混合预测模型，结合深度学习算法XGBoost提高预测模型的精度，并与直接预测模型和不同预测算法模型效果进行分析比较，进一步验证该混合预测模型的优越性。

最后，构建基于LMD-KPCA的转子故障预警模型，利用正常工况下的历史数据计算出两个故障监测指标的阈值，表征状态监测过程中故障信息偏离正常模型的程度，避免了人为设定阈值的局限性。输入预测值进行监测指标分析，设定每小时超出阈值的比例上限，从而实现转子故障的早期预警。

2.1 混合预测模型构建

根据局部均值分解理论和极端梯度提升算法原理，建立转子振动信号的混合预测模型。模型构建步骤如下：

1）将转子振动数据划分为训练集和测试集并进行降噪处理。

2）对训练集的数据进行局部均值分解，得到若干个不同时间尺度的子序列PF。

3）选择波动程度相近的子序列进行重构，分别得到高频子序列和低频子序列。

4）利用时间滑动窗口分别将高低频子序列变换成特征图，建立用于XGBoost预测的学习样本。

5）初始化XGBoost模型参数，对树的深度、树的数量、样本权重、学习率等参数进行调优，通过多次迭代更新参数使误差最小，输出高低序列预测值。

6）对预测信号进行重构，利用测试集数据验证预测效果。

为了评价转子振动信号混合预测模型的性能，本文选择平均绝对误差（mean absulute error,MAE）、均方根误差（root absulute error,RMSE）和拟合度（goodness of fit,R2）作为模型评价指标，各指标计算公式如下：

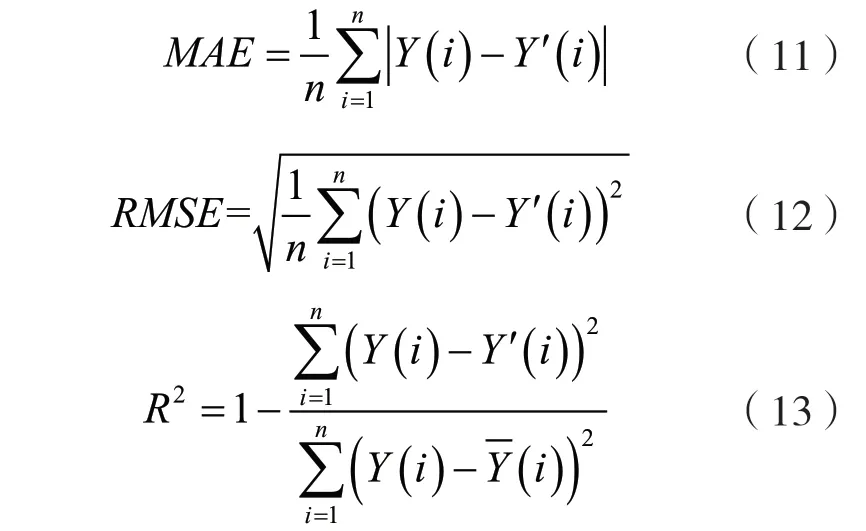
式中：n为时间序列长度；i=1,2,…，n；Y(i)、Y＇(i)、和分别表示第i个采样时刻燃气轮机转子振动位移的实际值、预测值和平均值。

预测模型评价指标中，RMSE越小则转子振动信号预测准确率越高，MAE越小则预测结果偏差越小，R2表示预测曲线和实际曲线的拟合度，R2越接近1，说明拟合效果越好。

2.2 阈值模型构建

阈值模型构建流程如图3所示。

图3 阈值模型构建流程图

结合局部均值分解方法和核主元分析构建转子故障预警的阈值模型，模型构建主要步骤如下：

1）确定转子正常运行数据，并将其作为样本数据。

2）对样本数据进行LMD分解获得多个不同尺度的PF分量。

3）对PF分量进行相似性重构生成高低频子序列。

4）建立高低频子序列相应的矩阵映射至KPCA模型，计算出正常工况下故障监测指标T 2和SPE的控制限。

5）将预测信号输入该阈值模型，计算出预测信号故障监测指标统计量，并与阈值进行比较，设置每小时监测指标超出阈值的比例为最终预警依据。

3 仿真结果及分析

3.1 数据来源及数据处理

本文实验数据来源于上海某燃气电厂两台F级燃机机组2019年5月1日至2019年12月30日的运行数据，两个数据采样点之间间隔为1 s，共计615个燃机运行相关变量，每组数据包含约130万行的数据。其中转子振动数据为16组，转子振动测点名称见表1。

表1 转子振动测点

本文首先通过自适应小波阈值法对原始振动数据进行降噪处理，并与普通小波阈值法进行降噪效果对比，验证了自适应小波阈值法在燃气轮机转子振动信号降噪上的有效性，其中原始信号波形、小波软阈值降噪信号波形、小波自适应降噪波形分别如图4、图5、图6所示。

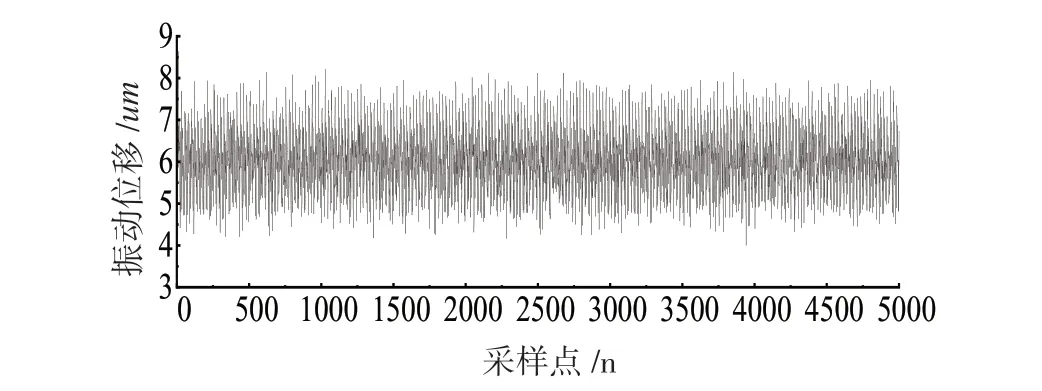
图4 原始数据信号

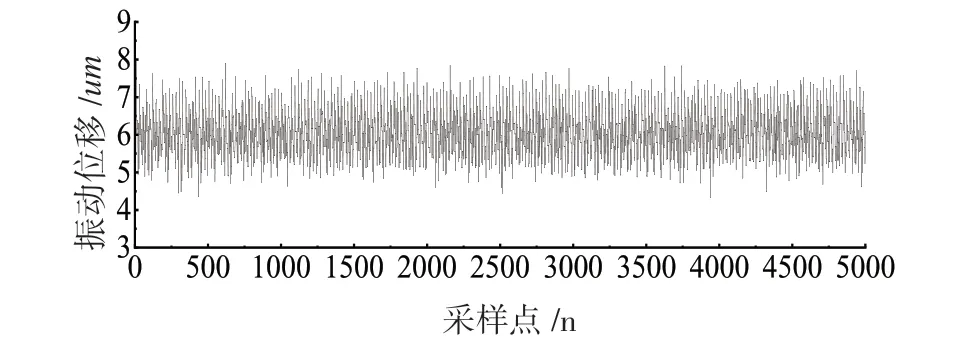
图5 小波软阈值降噪信号

图6 小波自适应阈值降噪信号

实验结果表明，自适应小波阈值降噪法对转子振动信号的降噪效果明显优于用传统的软阈值或硬阈值函数进行小波阈值降噪的效果，经过自适应小波阈值降噪后的振动信号时域波形呈现有规律波动。

3.2 混合预测模型效果验证

为了验证混合预测模型的效果，选取2 000个样本数据作为训练集，并用接下来的300个数据样本作为测试集对该模型进行验证。

首先对降噪后的数据进行局部均值分解，LMD方法通过改变信号分解过程能有效改进EMD方法存在的包络拟合不准确、边界处发散等问题，具有端点效应小、迭代次数少等优势，经过局部均值分解得到5个不同的PF分量，能够清晰准确地反映出信号能量在空间各尺度上分布规律的时频分布，得到更细致的信号特征，PF分量图如图7所示。

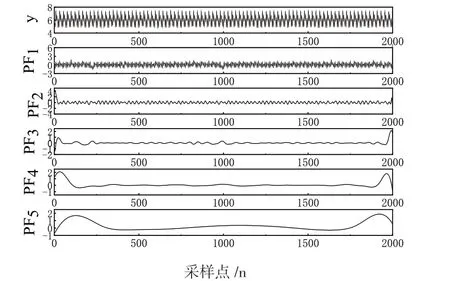
图7 PF分量图

不同时刻的转子振动信号经过LMD分解得到的PF分量的数量不一致，预测对象的不确定不利于预测模型的建立，也给后续基于核主元分析的故障监测增大了难度。因此在获得PF分量的基础上，选择波动频率较高的PF1、PF2、PF3分量进行时域叠加得到高频子序列，将波动频率较低的分量PF4、PF5进行时域叠加得到低频子序列，如图8所示。

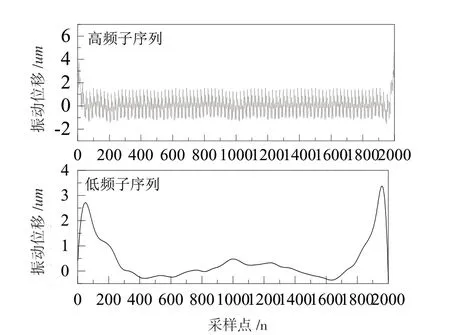
图8 高、低频子序列

通过使用滑动时间窗口依次将高低频子序列X(T)变换为特征图输入XGBoost模型进行预测，输入的特征图格式如下所示：

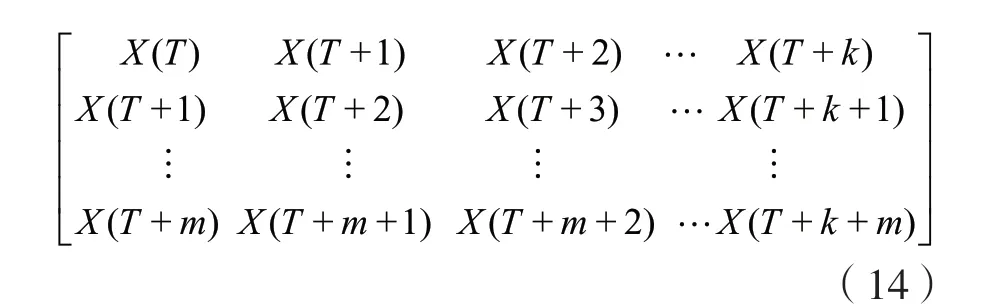
使用XGBoost算法分别对高、低频子序列进行预测并重构得到最终预测信号，通过与XGBoost算法和LSTM模型对未分解信号的直接预测效果对比，验证该混合预测模型的效果，如图9所示。

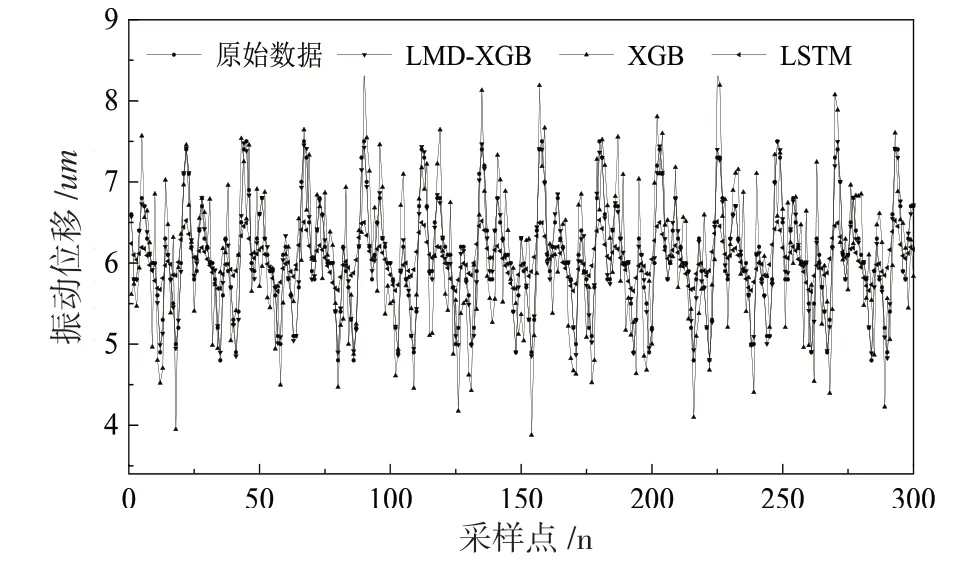
图9 预测模型结果对比图

计算3种预测模型的评价指标均方误差、平方绝对误差和拟合度见表2。

表2 预测模型评价指标

实验结果表明，XGBoost直接预测振动信号效果优于LSTM算法，而LMD-XGB混合预测精度进一步提高。

3.3 故障预警效果分析

该电厂3号燃气轮机机组2019年8月9日上午12时发生燃气轮机振动异常，并在后续运行过程中，振动出现增加的趋势。为了保证机组安全运行，降低故障风险，将该燃机设置为紧急备用状态。经过机组检查和振动试验找出导致3号机组振动异常的原因为转子质量不平衡，并通过转子动平衡配重有效降低了机组振动幅值。

选取正常工况下5-6月份的数据，通过LMD-KPCA模型计算出正常工况下的平均阈值，作为后续故障检测指标阈值，见表3。

表3 故障监测指标阈值

为了验证LMD-XGB-KPCA预警模型的有效性，从电厂SIS系统中选取此次故障发生前6天的运行数据进行建模，用前5天（8月3日-8月7日）的数据作为训练集对预警模型进行训练，对后2天（8月8日-8月9日）的数据进行预测，故障发生前预测信号SPE和T 2变化情况如图10、图11所示。

图10 监测信号故障指标T2

图11 预测信号故障指标SPE

正常工况下SPE和T 2上下波动但基本处于阈值线下方，故障发生前统计量超出阈值的比例明显增加，计算出预测信号每小时超出阈值的比例和，如图12和图13所示。根据燃气电厂运维经验，若设置当>0.48，>0.48时进行预警，由预警曲线图显示出，T 2指标预警时间大约为2019年8月8日晚上11点左右，SPE指标预警时间为2019年8月8日晚上10点左右，相对于故障时刻提前了13个小时，且SPE指标比T 2指标更敏感，在故障监测时更加灵敏。

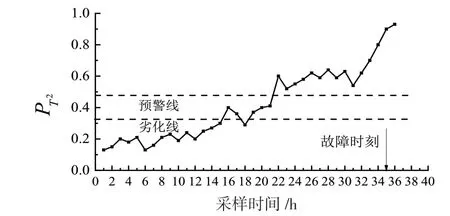
图12 故障监测指标T 2预警时间

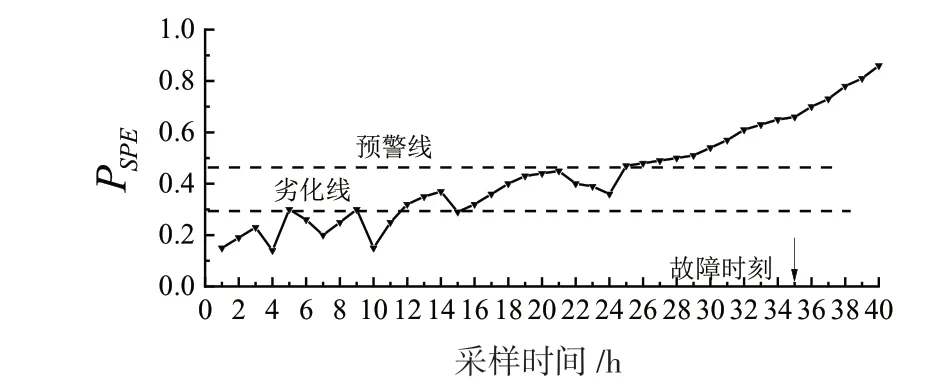
图13 故障监测指标SPE预警时间

4 结论

转子作为燃气轮机整机设计的核心，故障占比极高，其可靠、稳定的运转直接影响到燃气轮机机组运行的安全性和经济性。本文以燃气轮机转子为研究对象，提出了一种信号分解和时序预测相结合的混合预警方法。对转子原始振动信号进行自适应小波阈值降噪，基于LMD分解方法和XGBoost算法建立燃气轮机转子振动信号模型，并结合LMD-KPCA阈值模型计算出的预警阈值，实现了燃气轮机转子的故障预警。实验结果表明：

1）自适应小波阈值法对燃气轮机转子振动信号具有更好的降噪效果，明显优于固定小波阈值方法。

2）基于LMD-XGBoost的燃气轮机转子振动信号的混合预测，相较于LSTM神经网络和XGBoost直接预测，其预测精度和效率更高。

3）建立LMD-KPCA模型，基于数据内部特征变化计算出预警阈值，避免了手动设置阈值的麻烦，提高了模型预警的准确性。