一类Riesz空间分数阶对流弥散方程的差分方法
张治国,陈豫眉,梁 倩
(西华师范大学a.数学与信息学院 b.公共数学学院,四川 南充 637009)
0 引言
分数阶偏微分方程已被广泛应用于生物、化学和物理等领域[1-6].由于应用背景广泛并且分数阶微分方程难以获得精确解,故求其数值解尤为重要.目前有不同的数值方法用于求解Riesz空间分数阶方程.Meerschaert等[7-8]应用移位的Grünwald-Letnikov公式逼近Riesz分数阶导数,提出了无条件稳定的一阶差分格式.Celik等[9]使用分数阶中心差分公式近似了Riesz分数阶导数,提出了无条件稳定的二阶隐式差分格式.刘桃花等[10]研究了带有分数阶边界条件的Riesz分数阶对流扩散方程,他们利用分数阶中心差分公式离散Riesz分数阶导数, 对边界条件中的左侧Riemann-Liouville分数阶导数使用标准的Grünwald-Letnikov公式离散.林海欣等[11]研究了带左侧Rieman-Liouville分数阶导数边界条件的对流扩散方程,他们利用分数阶中心差分算子离散Riesz分数阶导数,同时对于边界条件则是使用加权和移位的Grünwald-Letnikov公式进行离散.尹修草[12]和曾宝思等[13]研究的分数阶对流扩散方程中含有带整数阶的Robin边界条件,利用中心差分公式离散Riesz分数阶导数.古传运等[14]推广了含Rieman-Liouville导数的分数阶微分方程的比较定理.
给定如下带有分数阶边界条件的Riesz空间分数阶对流弥散方程:

(1)
u(x,0)=q(x),0 (2) (3) (4) 定义中Γ(·)为Gamma函数. 本文主要讨论β>0时的情况. 均匀剖分给定区域 (N,M∈Z+)分别为空间及时间步长,则xi=ih(i=0,1,…,N),tm=mΔt(m=0,1,…,M).再令φi=φ(xi), Celik等[9]定义如下分数阶中心差分算子: (5) 其中 利用(5)式对(4)式在点(xi,tm)进行近似处理,即: (6) 利用向后Euler差分近似一阶时间导数,得: (7) 林海欣等[11]利用加权和移位的Grunwald-Letnikov公式对(3)式中的分数阶导数进行离散,得到 (8) 其中 在时间层t=tm(m=1,2,…,M),及(6)-(8)式可以得到(1)-(3)式的如下隐式差分格式: (9) 由此可知,差分格式(9)与原方程(1)-(3)是相容的. (10) 将(10)式改写成矩阵形式:AXm=Xm-1+Fm,1≤m≤M,其中 A是一个N×N系数矩阵: 定理1.1隐式差分格式(9)的解满足存在唯一性. 证明结合引理1.1可知: 结合引理1.2可知,当i=N时, 即矩阵A是严格对角占优的,由其可逆性可得:差分格式(9)的解存在且唯一. 定理1.2差分格式(9)是无条件稳定的. (11) (12) (13) (14) 运用(14)式(m-1)次,得 ‖εm‖∞≤‖εm-1‖∞≤…≤‖ε0‖∞. (15) 由(11)-(15)式可以得到,差分格式(9)无条件稳定的. 证明由em的定义可以得到: (16) 由引理1.2和Stirling定理,有 (17) (18) 运用(18)式(m-1)次,得 (19) 由(16)-(19)式可以得到: ‖em‖∞≤C(Δt+h2). 通过(16)-(18)式可以知道差分格式(9)是收敛的,其收敛阶为O(Δt+h2). 考虑以下方程: 其中 初边值条件为: 该方程的准确解是u(x,t)=e-tx2(1-x)2.这里β=1,α=1.5. 图1 数值结果 表1 最大误差和时间收敛阶,其中 表2 最大误差和空间收敛阶,其中 表3 文献[10]中的最大误差和收敛阶 本文研究了带有分数阶边界条件的一类Riesz分数阶对流弥散方程,通过中心差分算子离散Riesz分数阶导数,对右边界点x=b处的分数阶导数采用二阶加权和改进的Grunwald-Letnikov公式离散,从而构造出隐式有限差分格式.理论分析了隐式差分格式解的存在唯一性、稳定性和收敛性,并通过数值算例验证了差分法的可行性.




1 差分格式构造及理论分析

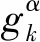
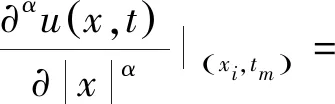







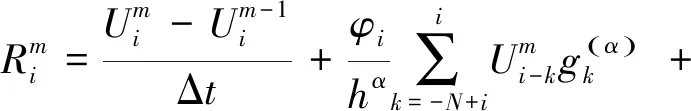



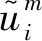


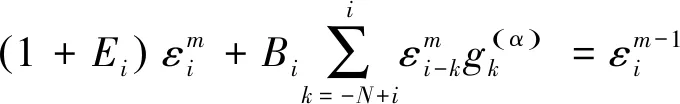




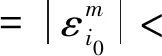





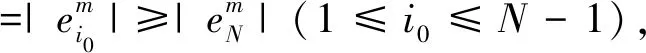

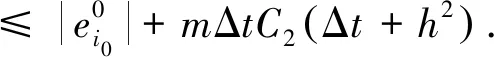
2 数值算例









3 结论

