差异化GFRP锚杆布设方案锚固效果研究

朱 俊， 张志强

(西南交通大学交通隧道工程教育部重点实验室， 四川成都 610031)

1 GFRP锚杆

锚杆深入边坡滑动面直至到达稳定的基岩处，以锚杆锚固段提供主要抗滑力来抵抗边坡失稳。GFRP(玻璃纤维增强聚合物)锚杆相较于普通锚杆，在岩土工程中具有更优越的性能，在近几年被广泛应用于边坡工程中。锚杆加固是保证边坡稳定的重要手段，因此研究锚杆的布设方案对边坡锚固效果的影响是必要的[1-3]。

针对锚杆的设计，国内外学者做了大量研究。王俊石[4]结合工程实践分析了锚索作用机理，建立了最优锚固角计算公式。封金财[5]通过理论推导了锚杆倾角取何值能提供最大抗力。熊文林等[6]考虑到坡面和滑面不平行的情况，提出了结合坡面和滑面倾角计算预应力锚杆方向角的方法。吴礼舟等[7]建立了膨胀土边坡加固模型，研究了锚杆布设角度和间距对边坡变形的影响。曹平等[8]通过有限元计算，研究了边坡稳定性随锚杆长度变化的规律。林杭等[9]剪力边坡模型，研究了锚杆长度和坡率和最优锚固角的关系。Hrycjw等[10]研究了锚杆不同布置组合对边坡稳定性的影响。shiuYK[11]等认为影响土钉边坡的主要因素有边坡高度、角度和锚杆的布设形式3点。

现有的大多数边坡加固工程中，对锚杆布设方案的来源和具体工作没有详细描述。且针对提及的加强边坡中下部支护以保证边坡稳定性的建议没有体现。GFRP锚杆由玻璃纤维、树脂合成加工制得，具有经济、性能优越的优点，应用于边坡工程的案例不多。针对以上问题，本文通过数值模拟，分析GFRP锚杆差异化布设方案对边坡稳定性的影响，对比获得最优锚固效果，为后续GFRP锚杆加固边坡工程提供依据。

2 数值模拟

2.1 计算模型

本次计算的公路边坡位于大理至丽江高速公路，根据现场量测后，简化边坡建立三维有限元数值计算模型，模型计算范围长为90 m，厚度为25 m，最高处至边坡底部取为50 m，如图1所示。

图1 数值计算三维模型

模型共计四级边坡，从下至上依次为1级、2级、3级、4级边坡，在其1、2级边坡采用GFRP锚杆支护，每级边坡及支护具体几何参数见表1。

表1 各级边坡及支护几何参数

采取不同锚杆间距和锚固角度组合布置形式共计10组工况来研究GFRP锚杆锚固角、锚杆间距对边坡加固效果的影响，具体工况信息见表2。

表2 各级边坡及支护几何参数

GFRP锚杆与边坡的空间关系见图2。

图2 GFRP锚杆与边坡的空间关系

2.2 材料参数

结合地勘资料确定土层的物理力学参数，将岩土分为基岩和风化松动层，其相应参数见表3，GFRP的材料组成为77.5%玻璃纤维、22.5%树脂，密度2.2 g/cm3，结合室内拉拔试验结果及GB1499.2-2007《钢筋混凝土用热轧带肋钢筋》确定锚杆参数见表4。

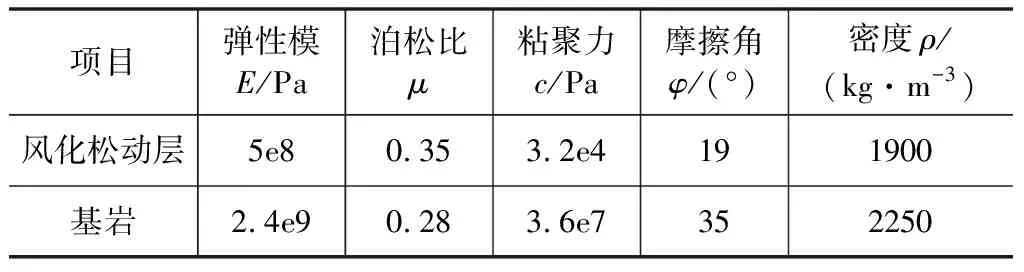
表3 土层物理力学参数

表4 GFRP锚杆物理力学参数

本次数值模拟为与实际工程更加接近，土层采用DP屈服准则，锚杆采用双线性随动强化BKIN模型。

3 结果分析

计算10组工况在自重条件下边坡的水平、竖直位移和剪应变，分析结果云图，对比锚杆发挥的锚固效果，寻找最优锚固角和锚杆间距。

3.1 水平位移变化分析

如图3所示的水平位移变化，采用锚杆加固边坡后，发生水平位移区域从风化层向内部移动。锚固角在12°、15°、20°一定情况下，水平位移随锚杆数量(锚杆间距与锚杆数量有直接关系)的增大而减小；锚杆间距一定情况下，水平位移随锚固角的增大而减小。

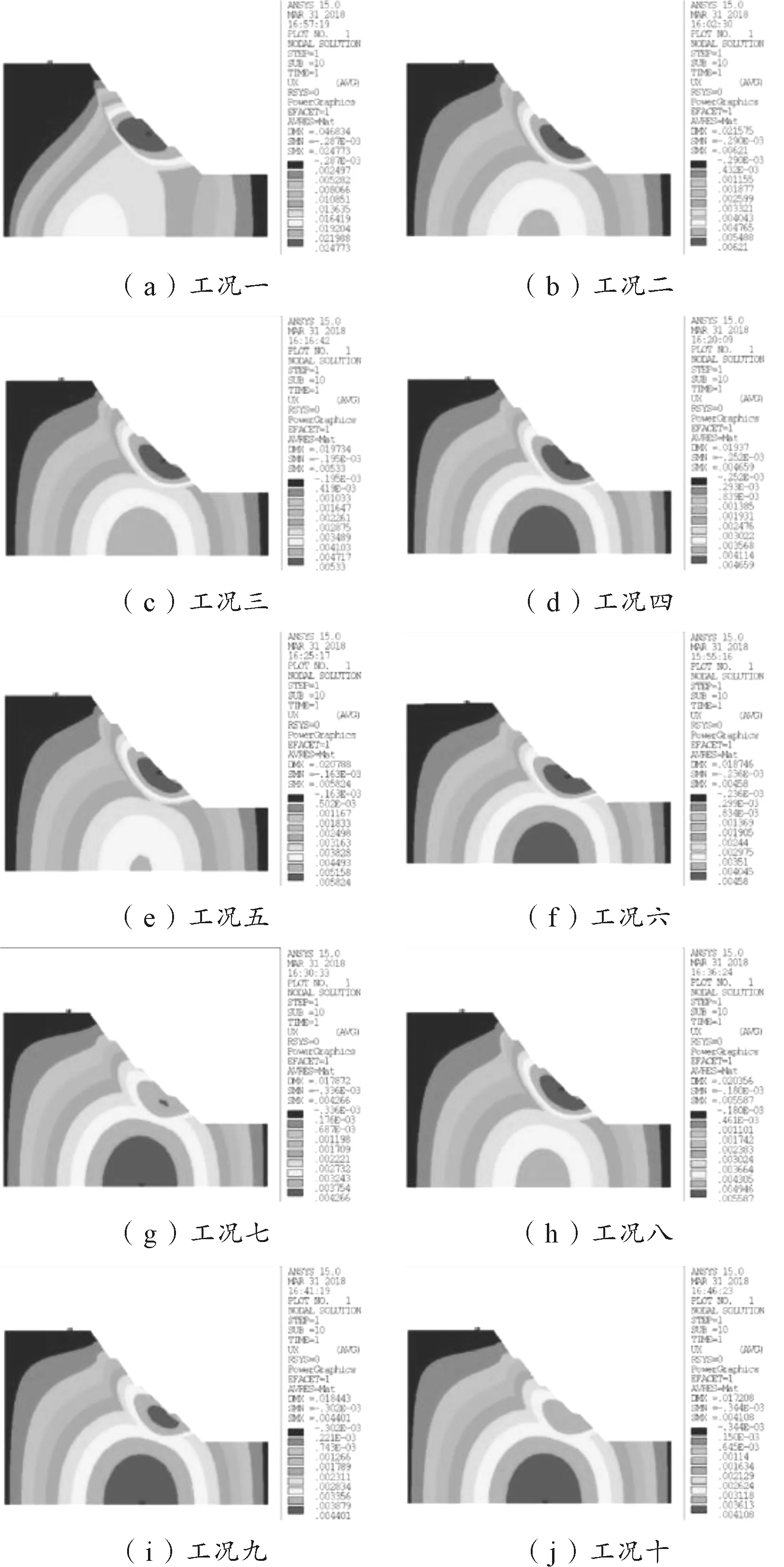
图3 自重条件下水平位移变化

3.2 竖直位移变化分析

如图4所示的竖直位移变化，采用锚杆加固边坡后，竖直位移分布规律无明显变化。锚固角在12°、15°、20°一定情况下，竖直位移随锚杆数量的增大而减小；锚杆间距一定情况下，竖直位移随锚固角的增大而减小。

图4 自重条件下竖直位移变化

3.3 剪应变变化分析

如图5所示的剪应变变化，采用锚杆加固边坡后，剪应变分布区域减小。锚固角在12°、15°、20°一定情况下，剪应变随锚杆数量的增大而减小；锚杆间距一定情况下，剪应变随锚固角的增大而减小。

图5 自重条件下剪应变变化

4 结论

采用差异化GFRP锚杆布设方案加固边坡，对比边坡位移和应变可以得到结论，为类似工程提供参考：

(1)锚固角相同，边坡水平位移、竖直位移和剪应变与锚杆间距成正比，即随着锚杆间距的减小而减小。

(2)锚杆数量相同，间距一定，边坡水平位移、竖直位移和剪应变与锚固角成反比，即随着锚固角增大而减小。

(3)针对本次四级边坡工程，当采用锚固角为20°，锚杆数量为每排8根，间距3.1 m×3.1 m时，位移和应变最小，可以认为这种工况下边坡最稳定，GFRP锚杆效果最优。