基于HCSR规范的加筋板载荷端缩公式修正
刘东,宋召军,b,万琪,许仁杰,李晓彬
(1.武汉理工大学 a.船海与能源动力工程学院;b.高性能船舶技术教育部重点实验室,武汉 430063;2.中国船舶及海洋工程设计研究院,上海 200011)
船体梁极限承载能力是反映船舶结构安全可靠的重要指标。评估船舶极限强度采用的主要方法有数值法、理论法、试验法、简化法(增量迭代法)。简化法评估船舶极限强度过程中,加筋板单元的载荷端缩关系直接影响简化法评估船舶极限强度的精度。在《协调共同结构规范》(IACS HCSR)中,受纵向压缩载荷加筋板失效模式分为梁柱屈曲、扭转屈曲,以及弹塑性失效等,不同失效模式具有不同的载荷端缩关系曲线。
目前有关加筋板的载荷端缩关系的研究主要集中在初始缺陷、残余应力等对加筋板载荷端缩的影响[1-7]。船体结构中甲板与船底板的加筋板单元主要由纵骨与带板组成,承载船舶航行遭受的静水与波浪引起的中垂中拱弯矩载荷,其常见失效方式包括梁柱屈曲、扭转屈曲,而板与板连接处为硬角单元。对于梁柱与扭转等屈曲模式研究较多,而硬角单元在受压时仅简单地假定为弹塑性失效,载荷端缩关系曲线为理想弹塑性模型。然而硬角单元的板格在受压过程中则会逐渐发生屈曲失稳,其载荷端缩曲线与理想弹塑性存在一定差异。因此,考虑通过简化法、试验法、非线性有限元法分析加筋板单元的平均载荷端缩关系,分析钢材材料属性对加筋板单元平均载荷端缩关系影响,对HCSR的加筋板单元载荷端缩公式进行适当修正,使更符合加筋板受压时实际的力学响应。
1 HCSR增量迭代法载荷端缩关系公式
HCSR采用增量迭代法评估船体梁极限强度时,船体横剖面被离散为一系列加筋板单元和硬角单元。在纵向受压作用下,不同板筋尺寸单元具有不同失效模式,其对应不同载荷端缩关系,公式见《协调共同结构规范》。
2 加筋板极限强度试验
2.1 加筋板试样尺寸设计
921A钢名义屈服强度为590 MPa,最薄板材厚度为5 mm,考虑到试验加筋板试样的最大载荷需小于微机屏显式液压万能试验机的最大工作载荷,试验加筋板试样范围选择1跨1纵骨,加筋板的试样尺寸参数见表1、2,其结构形式见图1。其中:λ为板柔度;β为梁柱柔度。
图1 加筋板几何模型

表1 921A加筋板主尺度 mm
2.2 试验装置装配
液压万能试验机的最大载荷为2 000 kN。加筋板试样上下端固定在试验机的上下平盘上,尽量保持加载中心与加筋板试样横剖面的形心重合,使加筋板端面受力均匀。在试样的上下端各安装1个百分表,分别记录试样的上、下端各自的位移变化。极限强度试验装配见图 2。

表2 AH32加筋板主尺度 mm
2.3 试验加载
对加筋板试样进行3段式加载,以预估极限强度的25%和50%分别作为在第一和第二循环载荷步的最大载荷,对加筋板试样进行两次预加载卸载循环。该过程位于加筋板的线弹性阶段,不产生塑性变形,但能减少焊接残余应力与装配间隙。对加筋板进行第三次位移加载和卸载,位移加载速度恒定且设为0.5 mm/min,加载载荷超过线弹性阶段,继续施加载荷进入加筋板的后崩溃阶段,然后开始卸载。
3 加筋板极限强度数值计算
3.1 有限元模型
实际船体加筋板结构的纵向边存在相邻加筋板的平动与转动约束,约束刚度介于刚固与自由边界之间,而极限强度试验的单筋加筋板两纵向边无约束,从而导致两者的极限强度存在一定的差异。单筋与3筋加筋板数值模型,其尺寸参数、范围模型、结构形式见表1和图1。
静态隐式非线性分析中,加筋板采用四节点的缩减积分SHELL181单元模拟,采用的AH32和921A钢的屈服强度分别为322和693.7 MPa,材料模型为各向同性的理想弹塑性,采用Von Mises屈服准则,弹性模量E=2.06×106MPa,泊松比μ=0.3。
加筋板的纵骨之间的带板网格划分16个单元,单元长宽比约为1,型材的型材腹板高度为6个单元,T型材翼板宽度为2个单元。
3.2 载荷和边界条件
船体结构为连续的多筋多跨板筋结构,其横向框架处的边界条件取决于横舱壁或强肋板的刚度,纵向边的边界条件则取决于横向框架间的距离。实船结构加筋板的均匀位移边界很难在试验中予以实现,所以试验中纵向边无任何约束而保持自由的边界条件;同时,考虑强肋板对纵向板筋尺寸约束的影响,加筋板两端横剖面采用附加的厚板固定。与试验一致的边界条件见表3和图3。

表3 加筋板载荷和边界条件

图3 加筋板载荷和边界条件
3.3 初始缺陷
加筋板结构在加工和焊接过程中产生的初始缺陷包含初始变形和焊接残余应力。焊接残余应力主要由焊接压应力和拉应力组成,压应力减少抗压能力,拉应力有助于抵抗压力,总体而言,焊接残余应力影响相对较小。因此,这里不考虑残余应力而仅考虑初始变形的影响。
加筋板的初始变形通常划分为板格的初始变形、筋的梁柱变形和筋的侧倾变形,计算如下。
1)板格的初始变形。
(1)
2)筋的梁柱型初始变形。
(2)
3)筋的侧倾型初始变形。
(3)

通过APDL(ANSYS程序设计语言)施加在加筋板的节点上,刚性约束首尾两端,静态分析求解初始变形。
4 加筋板载荷端缩关系
4.1 梁柱屈曲
试验法、数值法、简化法计算921A和AH32钢加筋板的平均载荷端缩关系见图4。
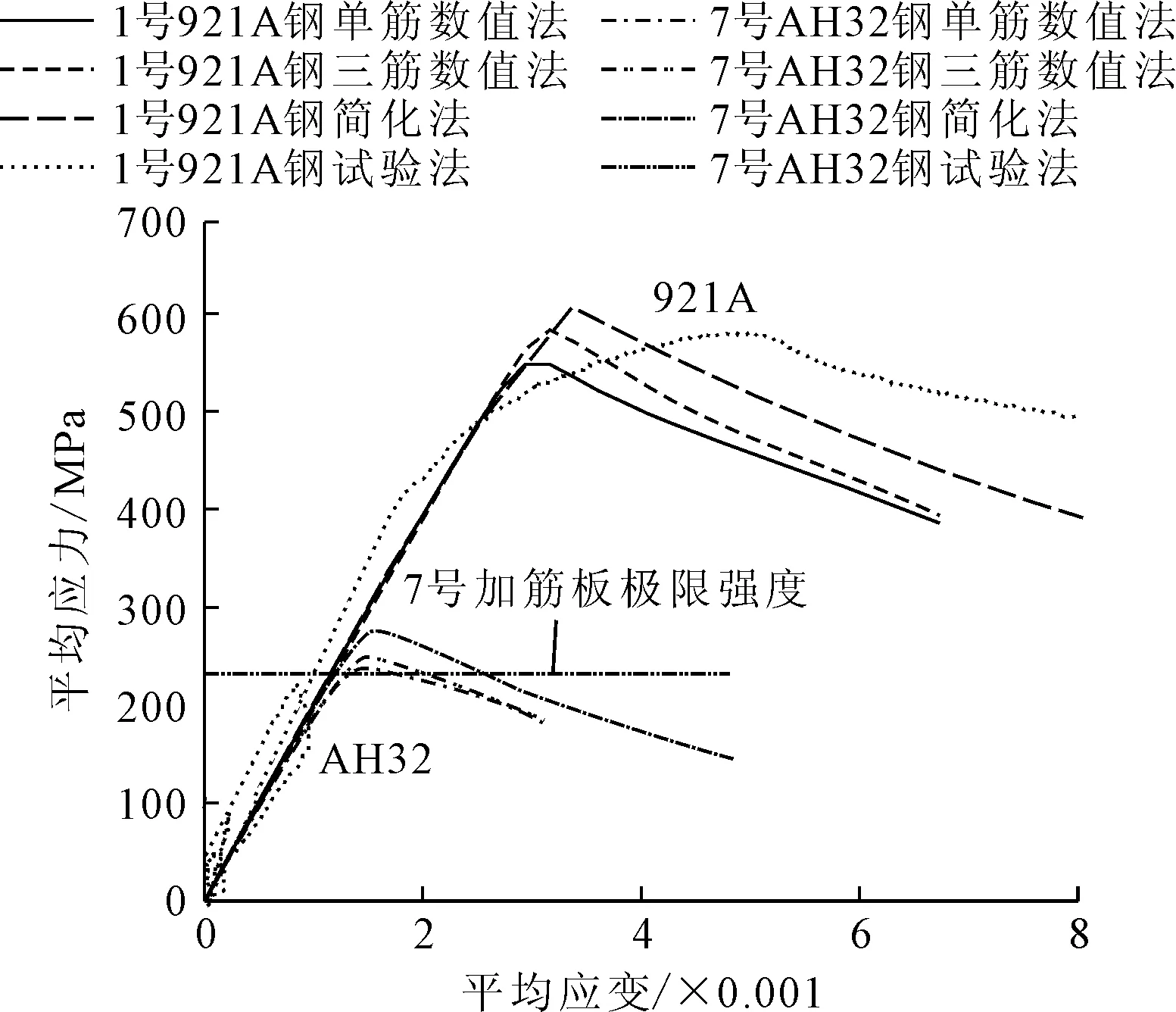
图4 1/7号试样加筋板载荷-端缩曲线
其中,载荷端缩平均应力等于端部载荷除以加筋板的横剖面面积,平均应变等于端部位移除以加筋板长度。在线弹性阶段,3种方法的平均载荷端缩关系均表现为线性关系,在后崩溃阶段,试验法与数值单筋的极限强度(即曲线最大值)相近。因此,试验验证了本文数值模型的合理性。由于数值单筋加筋板模型为纵向边无约束的自由状态,由数值3筋模型可考虑相邻板筋对中间加筋板承载力的影响,数值单筋极限强度小于数值3筋的结果,而数值3筋结果可得到与实际船体结构相近的极限强度,以与简化法的载荷端缩关系曲线进行对比。
1号加筋板试样崩溃永久变形见图5,梁柱屈曲的加筋板极限强度见表4。

图5 1号加筋板试样的崩溃永久变形实物

表4 梁柱屈曲的加筋板极限强度 MPa
由图5和可知,921A钢的1号加筋板的试验与数值结果中的总体变形规律一致,加筋板的筋和带板首尾端部区域变形不明显,中间区域的筋和带板发生较为严重的屈曲面外变形,屈曲模式均为梁柱屈曲模式。从表 4可知,1号、2号921A钢加筋板试样数值3筋与简化法的极限强度比值分别为96.1%,99.1%,而AH32钢加筋板相应的极限强度比值为90.9%,表明材料屈服强度低的加筋板易发生梁柱屈曲的弹塑性崩溃,HCSR规范的梁柱屈曲载荷端缩关系公式的评估误差虽在10%之内,随着材料屈服强度的降低可能增大。
4.2 扭转屈曲
扭转屈曲的加筋板极限强度见表5,3、8号试样加筋板载荷-端缩见图6。从表5和图7可知,3号、4号921A钢加筋板试样的数值三筋与简化法的极限强度比值分别为96.5%和100.5%,而8号AH32钢相应的极限强度比值为94.8%,表明材料屈服强度低的加筋板易发生扭转屈曲的弹塑性崩溃,HCSR规范的扭转屈曲载荷端缩关系公式的评估误差可能随钢材屈服强度的减小而增大。

图6 3/8号试样加筋板载荷-端缩曲线
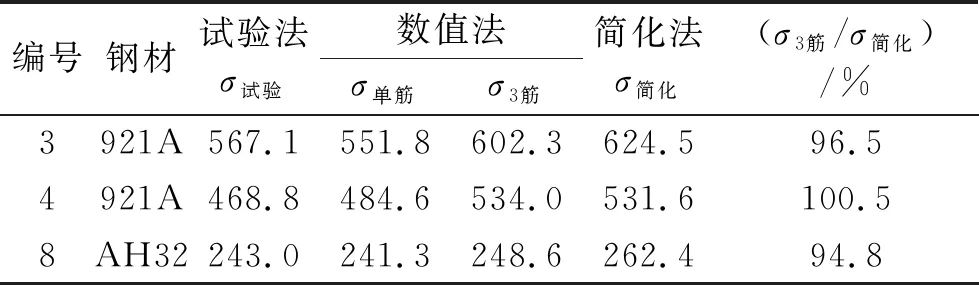
表5 扭转屈曲的加筋板极限强度 MPa
如图7所示,加筋板筋和带板首尾端部区域变形不明显,中部的带板面外屈曲变形明显,中部的筋发生扭转屈曲变形。

图7 3号加筋板试样的崩溃永久变形实物
4.3 硬角单元
5、9号试样加筋板载荷-端缩见图8。
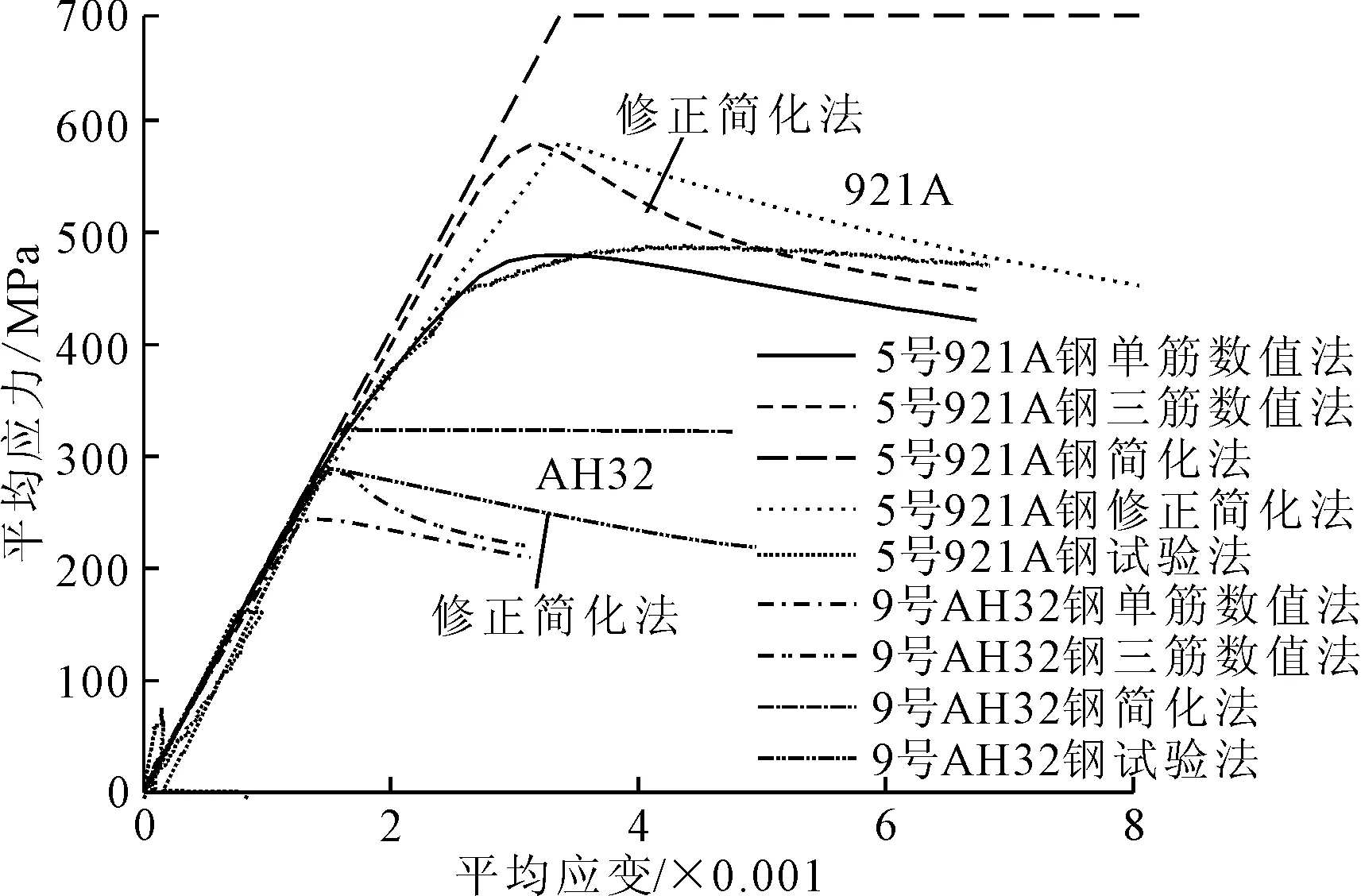
图8 5/9号试样加筋板载荷-端缩
由图8可知,921A和AH32的加筋板载荷端缩关系曲线在弹塑性响应的塑性变形阶段差异显著,尤其是在最大值和后崩溃的下降段,简化法的最大值远大于其他方法的最大值,简化法采用理想弹塑性,发生屈服失效后无下降段,其余两种方法崩溃后均有下降段。
从图9可知加筋板的首尾端区域没有产生变形,中部带板发生明显面外挠度变形。说明实际船体结构的硬角单元在受压作用下亦会发生板格的屈曲,甚至崩溃破坏,而简化法的理想弹塑性响应难以反映出硬角单元的真实变形过程,可能造成极限承载能力的高估。

图9 5号加筋板试验试样崩溃永久变形
硬角单元的极限强度见表6。从表6可知:921A钢的5号和6号硬角单元加筋板数值3筋与简化法的极限强度比值分别为83.6%和77.3%,而材料为AH32的硬角单元加筋板数值三筋与简化法的极限强度比值为90.00%。

表6 硬角单元的极限强度 MPa
说明在相同尺寸条件下,采用屈服强度小的钢材加筋板在受压时接近于弹塑性崩溃失效,而屈服强度大的高强度钢加筋板则发生板材局部屈曲,现有HCSR硬角单元的载荷端缩公式会显著高估高强度钢加筋板极限强度。
硬角单元由普通加筋板单元的带板组成,而普通加筋板的带板在受压载荷时亦会出现板格屈曲现象,造成硬角单元承载能力的降低,规范中的硬角单元理想弹塑性力学模型可能存在高估船体加筋板极限强度,特别是薄板引起的板格屈曲模式时。因此,依据板格的临界屈曲应力公式,结合板格的面积进行平均,修正硬角单元的平均载荷端缩曲线关系。适用于船体梁横剖面板板相交的硬角单元极限强度计算。
(4)
式中:si(i=1、2)为硬角单元两侧的板材宽度;bEi(i=1、2)为硬角单元两侧的板材有效宽度。

当βEi≤1时,bEi=si。

修正后简化法与数值3筋的极限强度相近,反应了实际船体结构硬角单元在受压作用下真实的力学响应,说明修正后的载荷端缩公式合理。
5 结论
HCSR规范中梁柱与扭转屈曲的加筋板载荷端缩关系误差随着钢材屈服强度的减小而可能逐渐增大;而硬角单元若采用理想弹塑性材料的载荷端缩关系曲线,会高估极限强度。所提出的硬角单元载荷端缩关系修正公式可反映其在受压过程中的实际力学响应,由该公式可获得真实可靠的极限强度。

