课本习题作用大 处处开花人人夸
陕西省西安高新第三中学(710075) 吕二动
题目(北师大教材必修五第二章第二节习题2-2,B 组第一题)如图1,一条直线上有三点A,B,C,点C在点A与点B之间,点P是此直线外一点,设∠APC=α,∠BPC=β.求证:

图1
此结论正是我们常说的张角定理(或三点共线定理),下面我们来具体看张角定理:
一、定理呈现
张角定理设A,C,B顺次分别是平面内一点P所引三条射线PA,PC,PB上的点,线段AC,CB对点P的张角分别为α,β,且α+β <180◦,则A,C,B三点共线的充要条件是:
证明如图2,A,C,B三点共线

图2

注若规定角的绕向,逆时针方向为正,否则为负,则上述定理、推论中的点C可表示在AB的延长线上的情形.
二、定理应用
1.解决向量相关问题



图3

图4


图5

2.解决解三角形相关问题
例4(2018 年江苏高考) 如 图6,在∆ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120◦,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为_____.
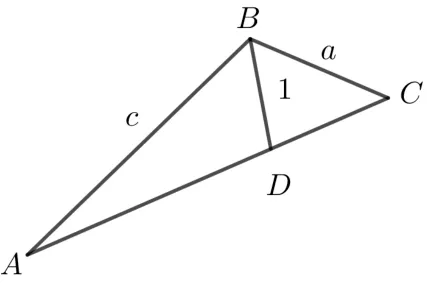
图6


图8
3.解决平面几何问题
3.1 线段长度之间倍分关系
例6已知G是∆ABC的重心,过G作直线分别交∆ABC的两边AB,AC于E,F.求证:EG≤2GF.



图9
例8(CMO-5 试题)如图10,筝形ABCD中,AB=AD,BC=DC.经过AC与BD的交点O任作两条直线,分别交AD于E,交BC于F,交AB于G,交CD于H,GF,EH分别交BD于I,J.求证:OI=OJ.
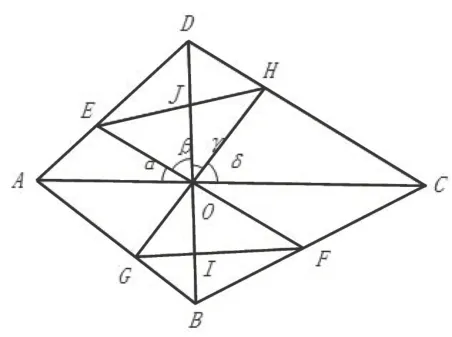
图10


3.2 证明线段长度成调和数列
调和数列: 如果一个数列的各项倒数成等差数列,则此数列叫做调和数列
例9如图11,已知AD,AE分别是∆ABC的内外角平分线,点D在BC边上,点E在BC边的延长线上.求证:

图11

例10如图12,圆的割线PAB通过圆心O,自P作圆的任一割线PCD交圆于C,D.又在圆上取一点E,使,连结CE交AB于F.求证:
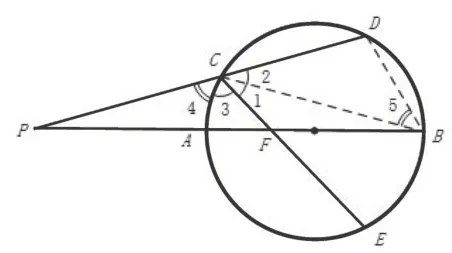
图12


3.3 证明线段长度成等差数列
例11(1979 年辽宁省竞赛题)如图13,已知AM是∆ABC的边BC上的中线,任作一直线顺次交AB,AC,AM于P,Q,N.求证:成等差数列.

图13
证明令∠BAM=α,∠MAC=β,∠AMB=θ.以A为视点,分别对P,N,Q及B,M,C应用张角定理,有

例12圆内接∆ABC,点C的切线交BA的延长线于P,过P任作直线交圆于E、F,交AC、BC分别于N、M,求证:
证明设∠APM=α,∠MPC=β,并分别取AB、EF中点G、H,如图14,显然P,G,H,C和圆心O五点共圆.
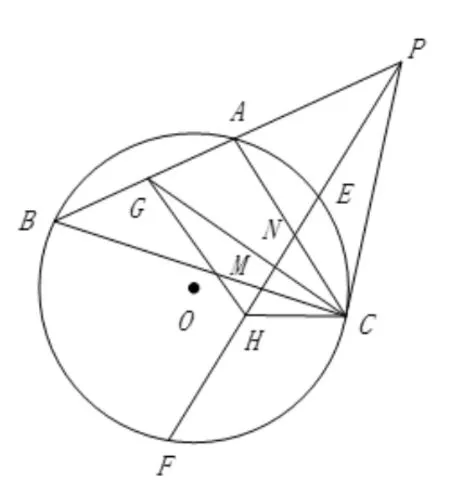
图14
由托勒密定理可知PH ·GC=GH ·PC+PG·HC,对∆GHC三边用正弦定理代入得PH ·sin(α+β)=PC·sinα+PG·sinβ,两边乘2,即

3.4 证明三点共线
例13如图15,已知AB是圆的直径,PA,PC是圆的切线,A,C为切点.作CD⊥AB于D,Q为CD的中点.求证:P,Q,B三点共线.

图15
证明以C为视点,考察线段PQ,QB所张的角的情形.连结AC,BC,则∠ACB=90◦,令∠PCA=α,则∠CBA=∠ACD=α,令PC=a,易知AC=2a·cosα,

3.5 张角定理与斯特瓦尔特定理的等价性
例14如图16,设B,P,C依次分别为从A点引出的三条射线AB,AP,AC上的点.线段BP,PC对点A的张角分别为α,β,且α+β <180◦,则B,P,C三点共线的下述两个充要条件等价:

图16

(Ⅱ)AB2·PC+AC2·BP=AP2·BC+BP·PC·BC(斯特瓦尔特定理).
证明
三、定理推广
推广1(3 维张角定理) 如图17,在四面体A −BCD中,P为棱DC上一点,若二面角D −AB −P为α,二面角C −AB −P为β,则

图17
首先证明引理: 四面体的体积等于任意两个面的面积之积的三分之二乘以这两个面所成二面角的正弦值再除以这两个面的公共线段之长.
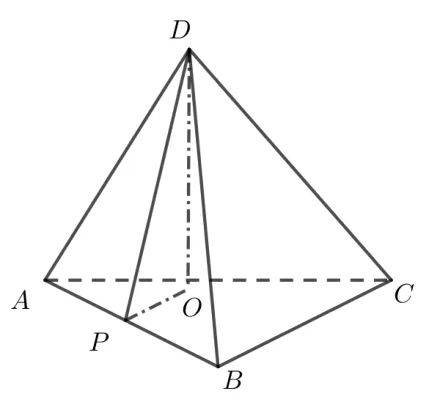
图18

例15(推广1 的应用: 1994 年高考) 如图19,已知A1B1C1−ABC是正三棱柱,D是AC中点.
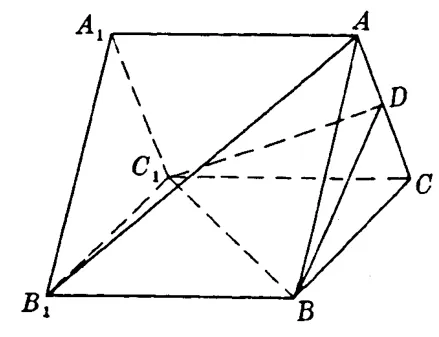
图19
(1)证明:AB1//平面DBC1;
(2)假设AB1⊥BC1,求以BC1为棱,DBC1与CBC1为面的二面角的度数.
解答(1)因为A1B1C1−ABC是正三棱柱,所以四边形B1BCC1是矩形.连结B1C交BC1于E,则B1E=EC.连结DE.在∆AB1C中,因为AD=DC,所以DE//AB1.又AB1平面DBC1,DE ⊆平面DBC1,所以AB1//平面DBC1.
图20



教材是我们学习的出发点和根源,高考、竞赛试题源于教材,把教材由薄读到厚,再由厚读到薄,对教材的每一道例题、习题,每一段文字,包括阅读材料,研究性学习都要认真思考,研究,只有这样,才能有收获

