基于自适应Kalman 滤波的智能电网假数据注入攻击检测

罗小元 潘雪扬 王新宇,2 关新平

智能电网是一种新型的电网,它采用先进的通信网络技术和控制技术来支持更高效的能源安全传输和分配.然而,由于智能电网系统的复杂性和开放性,智能电网中进行数据交换的信息网络成为易受到恶意攻击的对象[1−2].例如,2016 年,黑客攻击乌克兰国家电力部门致使国内发生了一次大规模的停电事件[3],造成严重经济损失.因此,智能电网的攻击检测研究具有重要意义.

隐蔽假数据攻击是目前恶意攻击的典型代表,攻击者对传感器节点注入精心设计的错误数据,接收错误数据的控制中心,继而做出错误决策破坏系统的稳定性[4].在文献[5]中,拒绝服务攻击旨在中断电力网络通信信道的可用性.文献[6]构建了一种对智能电网中以完整性和可用性为目标的攻击分类方法.文献[7]解决了在电力网络中攻击检测和拓扑隔离的问题.文献[8]提出了一种算法来识别要操作的智能电表的最优数目,从而找到最优攻击策略,其目的是干扰电网系统的状态估计,影响其稳定性.文献[9]设计了具有隐蔽特性的虚假数据攻击,它可以使攻击前后残差基本不变,因此,基于卡方检测器的检测技术是无效的.近年来,隐蔽性攻击检测成为了研究热点之一.

针对智能电网遭受虚假数据注入攻击的检测问题,近年来有了很多成果.文献[10]中,以电机的电压模型为研究对象,使用卡尔曼滤波(Kalman filter,KF)技术得到该系统的残差序列,通过计算攻击前后残差序列之间的Bhattacharyya 距离来判断系统中是否存在攻击.该文献的不足之处有两点:1) Bhattacharyya 距离无法辨别虚假数据注入攻击前后两个残差序列的相似性,因为虚假数据注入攻击前后残差保持不变;2)该电压模型是线性的,对于实际中存在的大多数的非线性系统,该检测算法是失效的.文献[11]使用卡尔曼滤波技术得到系统的状态,从系统状态角度考虑设计检测算法,提出欧几里德检测方法,该方法可以检测隐蔽假数据注入攻击.该文献的不足之处是,系统方程对于噪声是线性的,即该噪声是加性噪声,当系统方程对于噪声是非线性的时候,噪声经过非线性变换,不再服从高斯分布,也就无法设计阈值,无法检测攻击.文献[12]中,攻击者可能会缓慢改变多个传感器的测量值,因此上述统计异常检测不会检测到个别受损的测量值,所以提出检测思想,这些测量值组合起来会导致状态变量远离其真值,然而,文中作出假设,控制中心收集到的测量值都是服从高斯分布的,并基于此性质设计了双边假设检验检测攻击.该文献的不足之处是,电网系统中的参数仅会在特定情况下服从高斯分布,而这种情况并不常见,且建模时没有考虑噪声,所以该文中的检测算法局限性较大.

因此,根据虚假数据注入攻击的特性,考虑系统非线性和噪声统计特性未知情况,本文提出一种基于自适应平方根无迹卡尔曼滤波器 (Unscented Kalman filter,UKF) 的智能电网隐蔽假数据攻击检测方法.该算法可以有效地、稳定地应用于非线性系统中对系统状态作出估计,依据系统状态设计检测算法检测攻击,并从检测指标的角度与现有算法进行对比.最后进行仿真实验,实验结果证明,所提出的基于该算法的攻击检测方法可以准确地给出状态估计值,从而检测出隐蔽攻击.

1 电网模型、攻击特性及问题描述

1.1 电网模型

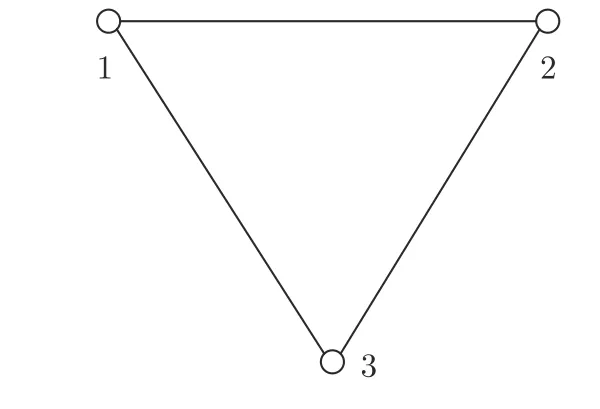
图1 3 总线电网模型Fig.1 3-bus grid model

式中,δi表示总线的相角,mi为转动惯量,di为阻尼系数,ui为控制输入信号,ηi是过程噪声,Pij是从总线i到j的有功功率流

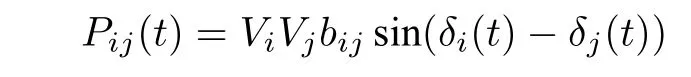
式中,V表示总线电压,bij表示总线i,j之间的电纳.

引入角速度ω,将上式改写为一阶微分方程组的形式,即

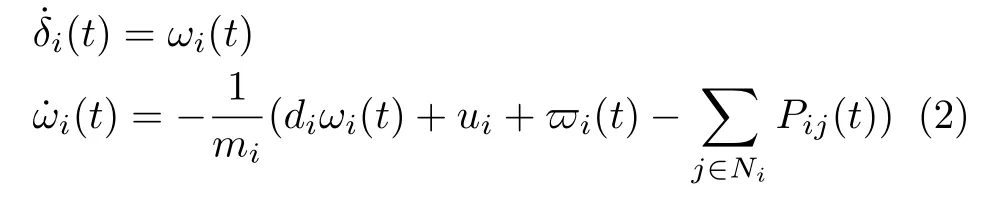
每一条总线都安装有传感器,将总线的数据传输回控制中心,系统输出方程为

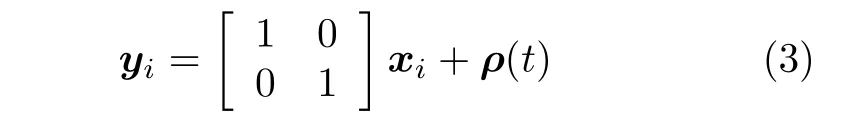
式中,yi表示总线i的输出向量,ρ是测量噪声.

针对上述系统,本文采用欧拉离散化方法[13],即对于一个非线性系统

离散化后的形式为

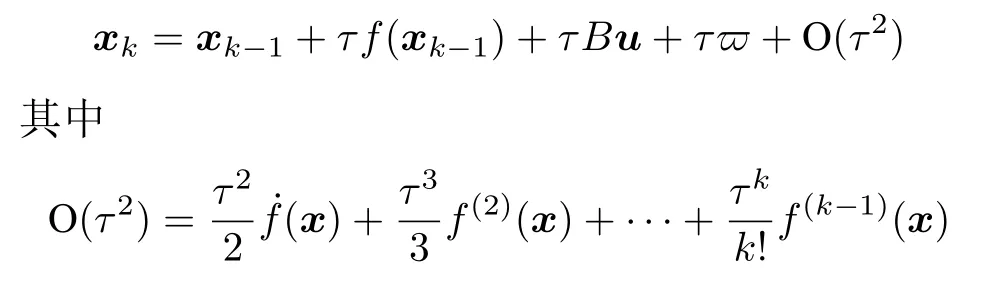
采样间隔值τ取值充分小以保证高阶项 O (τ2) 忽略不计,本文中τ=0.1 s.

对式 (2) 使用上述欧拉离散化算法对该系统离散化,得到

其中,fo(·) 表示关于x的非线性函数,将xk−1+τf(xk−1) 合并在一起,Bo=τB,η=τϖ.

假设η和ρ是互不相关的非零均值高斯白噪声,统计特性为

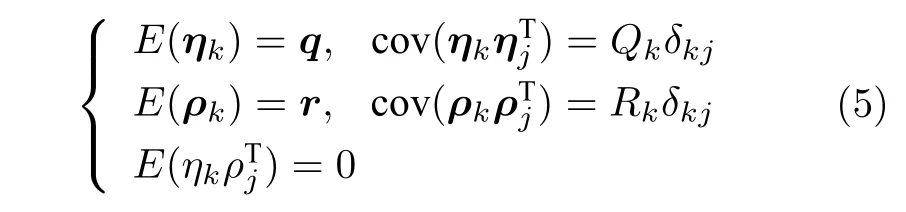
式中,Q是非负定矩阵,R是正定矩阵,δkj是Krone cher-δ函数,即

1.2 攻击描述和问题提出

假设一个恶意的第三方想要破坏第1.1 节中描述的系统的完整性.本文主要考虑虚假数据注入攻击.

假设攻击者具有系统知识,知道系统矩阵,控制矩阵,测量矩阵,可以控制一系列系统中的传感器数据.

考虑假数据注入攻击模型描述为

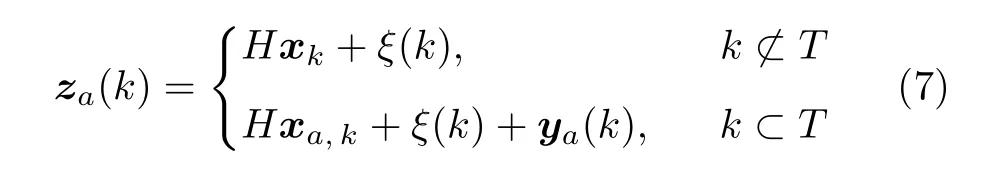
式中,Γ=diag{γ1,···,γn}代表传感器选择矩阵,T是攻击的时间范围,当γi=1 时,代表第i个传感器遭受攻击,否则γi=0 .且ya(k) 是攻击者精心构建的攻击向量序列,攻击框图如图2 所示.

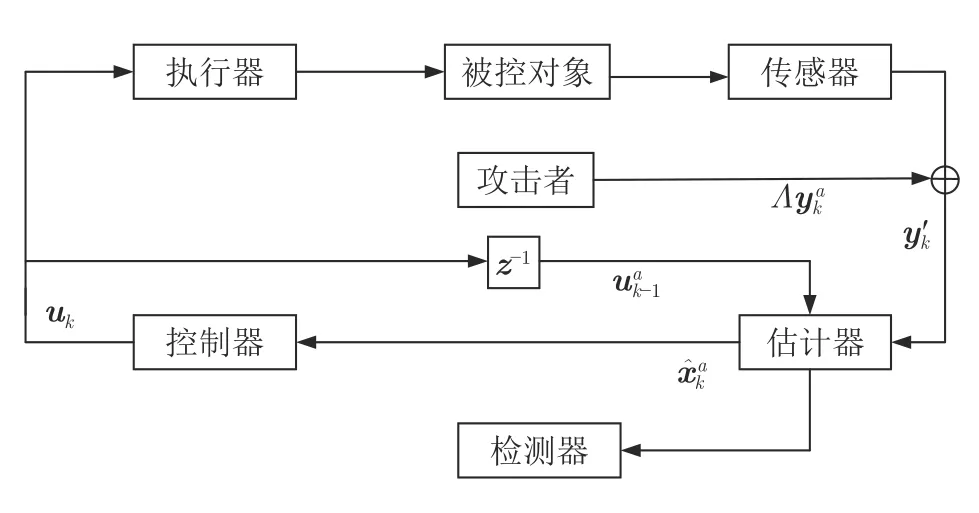
图2 系统遭受攻击框图Fig.2 block diagram of system under attack

在隐蔽假数据注入攻击情况下,在所考虑的攻击模型中,攻击者构造攻击序列注入传感器,在该序列下,状态差值最终将发散到∞,而不会触发卡方检测器.该攻击序列满足以下性质[9]:

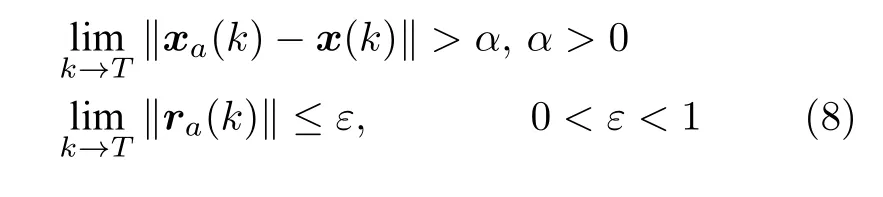
其中,xa(k)和ra(k) 是遭受攻击时系统的状态变量和残差.对攻击者克服检测机制的隐蔽性进行分析[4].由输出方程可得

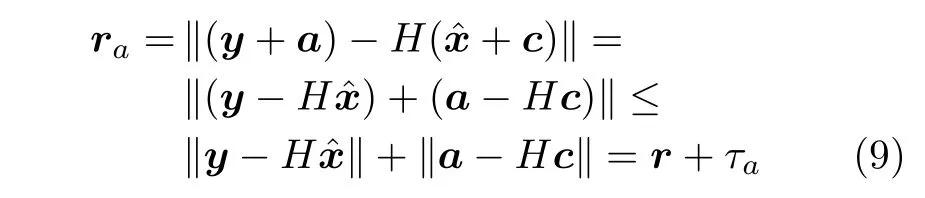
式中,a表示攻击信号,表示状态估计值,c表示状态变化量.由式(9)知,当a=Hc时,ra=r,从输出残差角度考虑,实现了隐蔽性.

由上述分析可知,从输出残差角度无法实现攻击检测.所以,需要借助滤波器从系统状态入手,利用状态差值检测攻击信号.本文考虑通过基于自适应平方根无迹卡尔曼滤波器的方法,从系统状态入手来检测此种攻击.

2 自适应平方根无迹卡尔曼滤波

本文提出将噪声估计环节[14]加入到无迹卡尔曼滤波算法中,实现对于噪声统计特性的在线估计,同时改变标准UKF 中状态误差协方差矩阵的迭代方式来保证滤波器的稳定性.

2.1 平方根无迹变换

本小节给出平方根无迹变换的实现方式.

步骤 1.利用k−1 时刻的估计状态及状态误差协方差矩阵来计算sigma 采样点ξi,并给出其权值Wm,i和Wc,i.

步骤 2.计算sigma 点通过非线性函数的传播结果

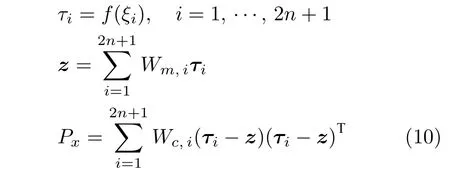
式(10)是无迹变换中的计算误差协方差矩阵的公式,平方根无迹变换将式(10)换为

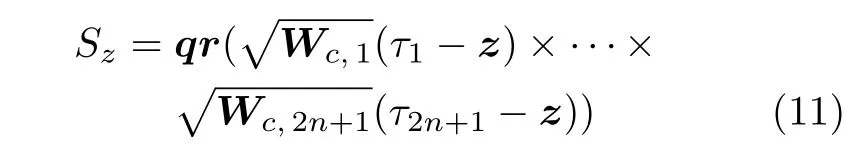
2.2 噪声估计方法

假设噪声是非零均值的高斯噪声,本文使用的是Sage-Husa 噪声估计器,通过极大后验估计原理,获得次优噪声估计值,噪声估计部分可参考文献[14].

对于系统(6),系统方程是非线性的,输出方程是线性的,所以噪声估计器为

2.3 自适应平方根无迹卡尔曼滤波设计

本节用到了MATLAB 中的3 个函数,分别为:qr 函数,cholupdate 函数,diag 函数.

1)qr(·) 表示QR 分解,A∈Rm×l,[Q,R]=qr(A),该函数生成m×l上三角形矩阵R和m×m酉矩阵Q,从而,A=Q×R.

2)R1=cholupdate(R,x),返回A+xx′的上三角Cholesky 因子,x是具有合适长度的一个列向量,其中,R=chol(A)是A的原始Cholesky 分解因子.

3) d iag{·}函数,D=diag{v},返回以向量v的元素为主对角线的对角矩阵.x=diag{A},返回A的主对角线元素的列向量.对于式(22)中最外侧的diag{·},返回一个对角矩阵,主对角线元素是每一次迭代得到的噪声矩阵主对角线元素的平方根的实时估计值.

自适应平方根无迹卡尔曼滤波(Adaptive square-root UKF,ASRUKF)算法的具体步骤如下.

步骤 1.初始化(k=1):

注1.Sage-Husa 噪声估计器不能同时处理过程噪声和测量噪声都未知的情况,否则会造成滤波发散,故上述算法假设测量噪声的均值和方差均是已知的[15].

注2.式(14) 的最后一个子式中,±表示当Wc,1>0时,取正;反之,取负,以保证根号下不出现负数[16].

2.4 自适应平方根无迹卡尔曼滤波稳定性

本小节给出自适应平方根无迹卡尔曼滤波算法的估计误差保持随机有界性的充分条件,并给出证明.

对于非线性电网系统(6)

式中

其中,βk=diag{β1k,···,βnk}为未知的矩阵,其作用是弥补建模一阶线性化引起的模型误差.

对于式(24)中的输出方程,定义

那么自适应平方根无迹卡尔曼滤波算法的状态估计误差将是均方有界的,即自适应平方根无迹卡尔曼滤波器稳定.

证明.选择函数

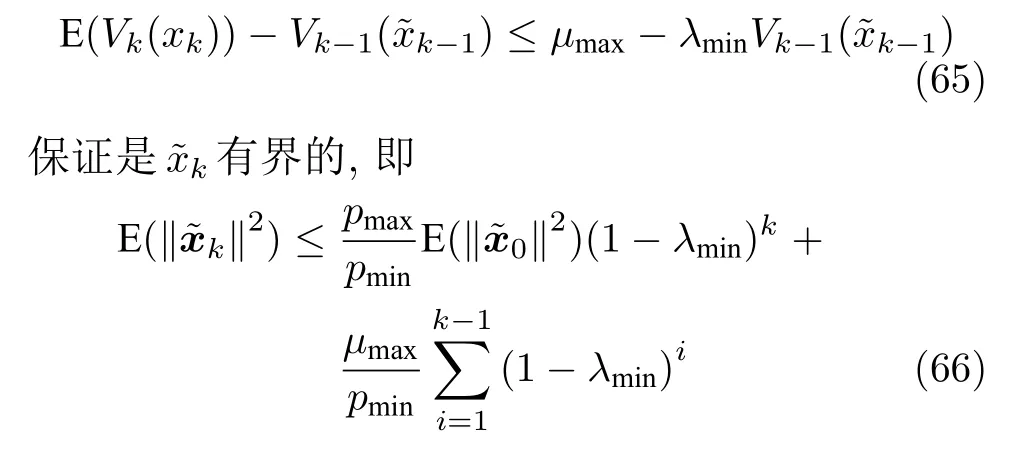
因此,自适应平方根无迹卡尔曼滤波算法状态估计误差将是均方有界的,即自适应平方根无迹卡尔曼滤波器是稳定的. □

注3.因为误差序列是随机过程,是该随机过程的均值函数,随机有界指该随机过程有界.即对于任意时刻k,对于服从高斯分布的噪声ω,定理1 确保了误差的2 范数平方的期望值是有界的,即上限α的值由定理1 确定.

3 检测方法

本节分析了文献[6],[10−11]中所使用的检测方法的不足之处.提出一种新的检测方法,利用中心极限定理设计新的检测算法,依据随机变量的统计特性提出双边假设检验法检测攻击,从误检率方面对本文算法给出分析,并与巴氏系数检测算法[10]、欧几里德检测算法[11]进行对比与分析.

文献[6] 针对虚假数据注入攻击,构造了CUSUM 算法来检测攻击.该算法步骤如下:

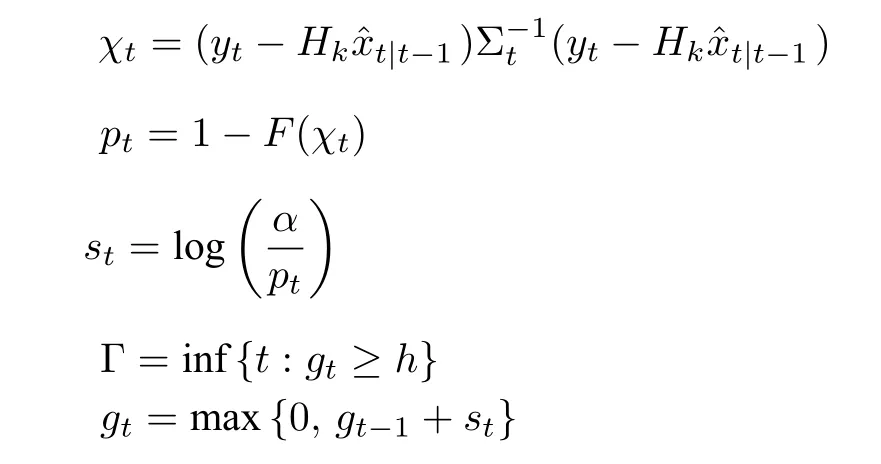
文献[6]中假设噪声服从高斯分布,可知χt服从χ2分布.F(·) 表示χ2分布的概率分布函数,pt表示χ2分布的上(右)尾概率,α表示系统给定的上(右)尾概率用于检验yt是否是异常值.根据χ2分布的上α分位点性质,当yt是异常值时,st >0;当yt是正常值时,st ≤0 .当yt是异常值时,gt的值会随时间累积直到超过检测阈值h(h的确定参考文献[6]),此时发出警报.该算法通过引入h,避免了欧氏检测算法那种仅考虑误检率的阈值设计方法,在误检率和误检周期之间做到了平衡,既降低了噪声的影响,又可以尽快检测出攻击.

但是,该算法实质上是依赖与噪声的高斯分布特性,即,实质上还是χ2检测,所以在遇到本文所研究的攻击时,攻击前后的残差基本保持不变,因此该算法是不可用的.

文献[10]中针对具有隐蔽性的复数域攻击,提出一种检测思想,滤波器在不受攻击下工作和滤波器在错误数据注入攻击下工作会产生两个服从高斯分布的残差序列,通过计算上述两个服从高斯分布的残差序列的巴氏相似性系数DB来判断攻击是否发生.

当物理系统的基本动力学用线性系统和高斯统计特性的噪声进行建模时,在正常操作期间,残差序列vo遵循零均值高斯分布vo=N(ro,So),攻击发生后残差序列

Bhattacharyya 距离无法辨别虚假数据注入攻击前后两个残差序列的相似性,因为虚假数据注入攻击前后残差保持不变.除此之外,该检测法的前提是线性系统,因为线性运算虽然会改变系统中随机变量的均值和方差但并不会改变随机变量服从高斯分布的特性,对于本文所研究的非线性系统,这种方法是不可用的.

目前存在的检测方法大多是在加性噪声的基础上提出的,在文献[11]中,假设过程方程和量测方程相对于噪声是线性的,即

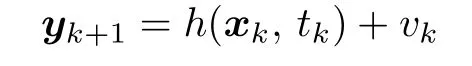
文献[11]中, 欧氏检测法的阈值和误检率正是基于噪声项的附加性得到的, 因为噪声并不参与到非线性变换中, 所以噪声的特性就是假设的正态分布的3σ特性, 使用正态分布的3σ原则设计阈值. 只有在这种前提下, 欧氏距离检测算法才是正确的. 实际上, 过程和量测方程相对于噪声也可能是非线性的,即

在这种情况下,欧氏距离检测法的阈值设计思想是行不通的,因为噪声不再作为附加项,而是直接参与到非线性变换中.此时,噪声不再服从正态分布,统计特性未知,因此阈值无法设计.

综上,本文提出一种检测思想: 在攻击未发生时,利用本文提出的非线性滤波方法,根据总线i上传感器在时间范围 [t0,tk] 收集到的测量数据获得系统状态估计值,进而获得后验状态误差值,此时并不知道状态误差这个随机变量服从什么分布,而且也不用对该随机变量的统计特性作出假设.本文将时间区间 [t0,tk] 分成l个小区间,对每一个小区间包含的使用中心极限定理[18]构造随机变量,得到l个,i ∈l,这l个随机变量是服从标准正态分布的,当攻击发生时,会偏离标准整体分布,从而达到检测攻击的目的.

本文所提出的检测方法从系统内部状态误差入手,不受限于传感器参数的概率分布未知所带来的影响,不受限于加性噪声和非加性噪声的情况,可以成功地完成攻击检测,并从数学角度给出了误检率与阈值之间的关系.

3.1 攻击检测

1)当系统正常运行时

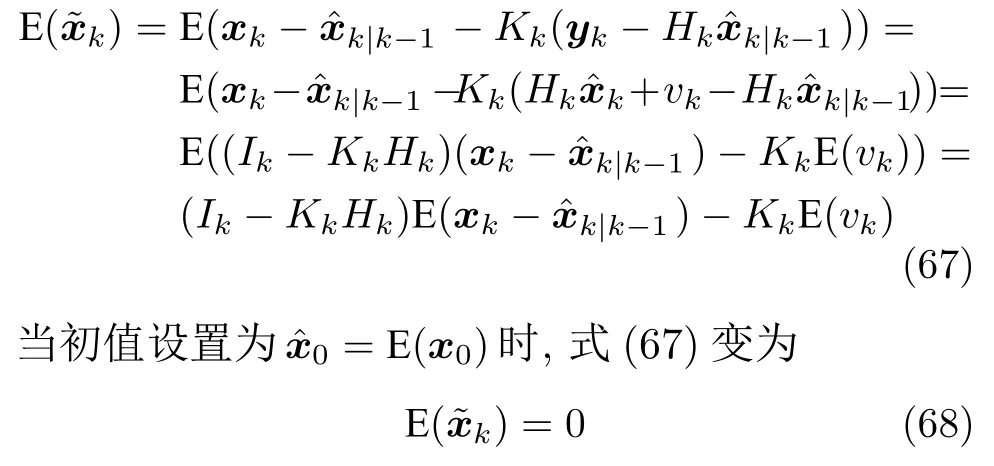
其中,q和r分别表示系统遭受攻击后均值和方差的变化.本文使用m和υ作为系统正常行为的度量.接下来,建立了一对阈值Tl和Th,用于检测系统是否遭受攻击,Tl=m −kυ,Th=m+kυ,表示允许偏离原数据的最大范围.当随机变量S[Tl,Th] 时,则确定系统遭受攻击[19].基于此,提出一个双边假设检验

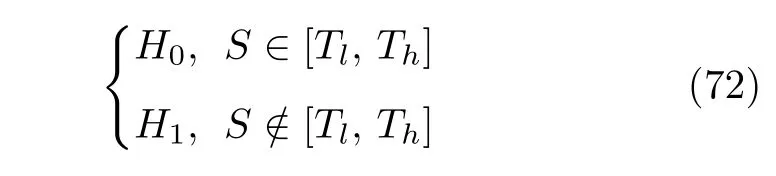
式中,H0代表系统没有遭受攻击,H1代表系统遭受攻击.

误检率PF的定义是攻击没有发生却宣布攻击发生的概率,即SN(m,υ),同时,|.

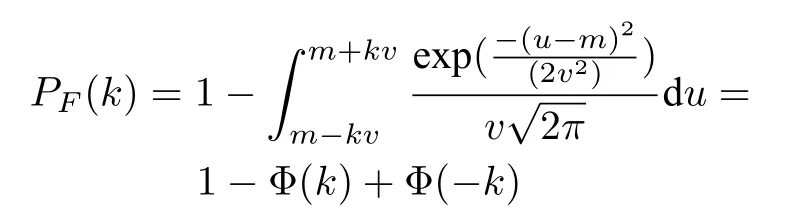
4 仿真

本节验证本文设计的自适应平方根无迹卡尔曼滤波算法估计状态及所提出检测算法检测攻击有效性,并与欧几里得检测方法进行对比.仿真参数和初始值为m=[8.9,8.8,8.5],d=[3.1,3.4,3.7],u=[6.3,1.6,8.5]T,B=[03×3;diag{1/m}].

为了最小化由噪声引起的误报率,欧几里得检测法的阈值设计采用 3σ准则(σ是噪声信号的标准差),那么得到先验阈值f=3σ=0.3.

4.1 ASRUKF 滤波算法的有效性

对于模型(6),未遭受攻击时的状态估计,从图3可以看出,ASRUKF 滤波器的滤波性能很好,滤波精度很高.

图3 ASRUKF 下的状态估计Fig.3 State estimation in ASRUKF

4.2 虚假数据注入攻击下的三种检测方法

1) 欧几里得检测法[11].由图 4可知,在迭代步数k=30 时刻对系统注入攻击,在k=80 时刻成功检测到攻击,欧几里得检测法可以成功检测出虚假数据注入攻击.

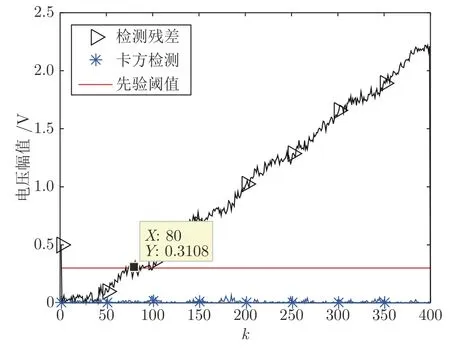
图4 两种检测方法针对隐蔽假数据攻击Fig.4 Two detection methods for covert false data attack

2) 巴氏相似性系数检测法[10].巴氏系数范围为0 到1 之间.越接近0,证明两序列越相似.由图5可知,巴氏相似性系数无法辨别虚假数据注入攻击前后两个残差序列的相似性,不可以检测出虚假数据注入攻击.

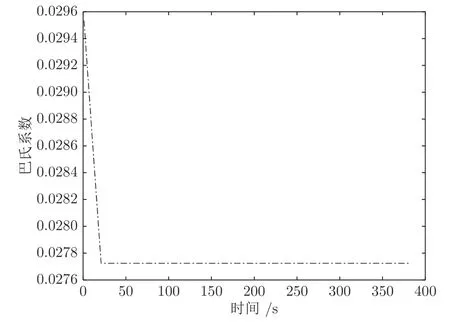
图5 巴氏相似性系数Fig.5 Bhattacharyya coefficient

3) 本文所提的检测方法.首先,使用分位数–分位数(Quantile-quantile,Q-Q)图来确定前面根据中心极限定理构造的分布可以近似为高斯分布.因为根据中心极限定理,随机变量的数量越多,它们的和也越近似服从高斯分布.然而,考虑实际情况,取无限多的独立随机变量是不符合实际的,所以在近似高斯分布的同时,要尽量选取较少的独立随机变量.要利用Q-Q 图鉴别样本数据是否近似于高斯分布,只需观察Q-Q 图上的点是否近似地在一条直线附近.

本文的检测算法选取了T=30 个独立随机变量参与运算,由图6 可知,数据的分布非常接近直线,这证明的分布可以视为高斯分布.

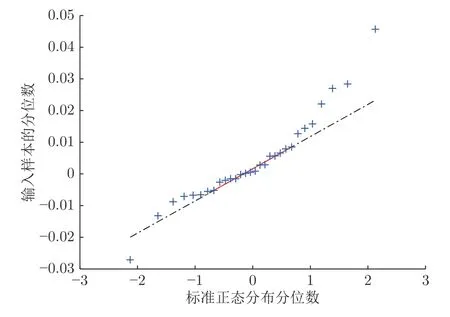
图6 S 的Q-Q图Fig.6 Quantile-quantile plot of S

由图7 可以看出,本文的检测算法对于隐蔽假数据攻击的有效性,在迭代步数k=30 处注入攻击,选取30 个迭代步骤下的随机变量构造出Sx˜,所以在k=60处超过了阈值,实现了攻击检测.

图7 本文提出的攻击检测方法Fig.7 Attack detection proposed in this paper

图8 给出了误检率随k变化的曲线.从图8 可知,一个算法的误检率过高,是因为阈值设置得太低,导致攻击之外的因素也会使得被检测的量超过阈值.随着k值增大,阈值变高,误检率自然随之下降.

在图8 中,当k=3 时,误检率PF=0.0027,除此之外,由图4 可知,欧氏检测法检测到攻击所用时间是 ∆k=50;由图8 可知,检测到攻击所用时间是 ∆k=30,检测用时更短.

图8 误检率PFFig.8 False alarm ratePF

综上,对比三种检测方法可知,本文提出的检测方法可以成功检测攻击不受限于传感器参数统计特性未知所带来的影响,不受限于加性噪声和非加性噪声的情况,对于实际系统的适用性更强.

5 结束语

本文研究了智能电网系统中虚假数据注入攻击的检测问题.针对非线性系统,噪声统计特性未知的情况,本文使用自适应平方根无迹卡尔曼滤波算法对系统内部状态和噪声作出估计.针对传感器参数统计特性未知和非加性噪声的情况,利用中心极限定理构造出符合正态分布的随机变量,基于该随机变量提出了一种攻击检测方法,并从评价指标的角度对算法进行分析,该算法对于实际系统的适用性更强.