面向快速响应的赛汝生产系统构建模型与方法

湛荣鑫 李冬妮 马涛 李俊杰 吴延昭 殷勇

自1980 年代以来,电子信息产业蓬勃发展,产品生命周期显著缩短,电子产品目前的平均生命周期仅为6 个月[1].因此,面对更为多样化的产品种类需求、更短的产品生命周期要求以及由此带来的市场环境波动性和不确定性[2−4],传统的生产系统如流水线或丰田制造系统难以获得很好的表现,亟需一种具有优异快速响应能力的新型生产系统[5].Seru是日式生产单元,由Seru 构成的赛汝生产系统(Seru production system,SPS)作为一种新兴的生产模式广泛应用于日本的电子制造行业.与传统生产系统相比,SPS 最突出的优势在于其应对不确定市场需求的快速响应能力,而之所以可以实现快速响应,主要原因就是Seru 在物理结构上是可重构而不是固定的,并由此可以带来诸如降低成本、缩短生产时间、缩短生产准备周期、缩短劳动时间等方面的显著收益[2,6−14].

目前,已有很多学者围绕SPS 构建问题展开研究,这类研究大多将SPS 构建分成了两个阶段,分别是Seru 构建和Seru 调度.Seru 构建大多分为两类模型,一类是研究如何将现有流水线拆分为若干个Seru;另一类是给定若干数量的Seru,主要考虑工人的分配问题[15].Seru 调度决策如何将产品批次分配到已构建好的Seru 中去[16−21].例如,Liu等[22]研究了在SPS 中多能工的培训和分配问题,建立了最小化总培训成本和平衡多能工之间劳动时间的多目标问题模型.Liu等[23]考虑了优化经济和环境指标的SPS 构建模型.Lian等[24]提出了考虑Seru 内部和Seru 间多能工劳动力平衡分配的SPS构建模型.

已有研究大多有一个共同的假设: 一旦Seru构建完成,就不再会发生变化.然而,SPS 应该具备随着生产需求变化动态进行Seru 构建和拆除的能力.此外,相关研究还大多假定工人都是全能工(即具有一个或多个产品所需要的所有工序的加工能力).实际中,工人很难全部被培训为全能工且存在技能水平上的差异.另一方面,纯粹由全能工构成的SPS 也不一定是最优的[25−26].因此,在考虑工人具有不同的技能组合和技能水平的情况下,如何组织工人构建SPS 是一个重要的研究问题.

基于以上考虑,本文考虑如下的SPS 场景并设计了两阶段的SPS 构建模型,分为Seru 构建(Seru configuration,SC)和Seru 调度(Seru scheduling,SS).当新订单到来时,有恰当数量的Seru 被构建并完成分配给各自的生产任务.当每个Seru 完成其生产任务时立刻拆解.因此,整个SPS 可以动态调整其自身结构,调整的对象包括Seru 的数目、分配给Seru 的工人以及每个工人负责的工序等.具体而言,两阶段描述如下.1) Seru 构建阶段: 在同一生产周期内,所有的工人具有同样的初始剩余工作时间.工人具有不同的技能组合以及在不同的工序上具有不同的技能水平,不同的工人在相同的工序上也具有不同的技能水平.首先在不超过每个工人工作时间上限的约束下,为订单找出一个可行的工人−工序分配方案,并在依照这个分配方案,考虑每个Seru 工人之间的配合从而构建Seru.在本阶段提出了工人−工序映射模型和优化Seru 内部工人工作时间平衡的工人−Seru 分配模型;2) Seru 调度阶段: 一个工人在Seru 构建阶段中可能会被分配参与多个Seru 的生产任务,而任一工人同一时刻只能参与一个Seru 的生产,因此Seru 间存在调度问题,基于此提出了最小化SPS 最大完工时间(Makespan)的Seru 调度模型.

本文的主要贡献如下: 1)考虑了工人并非全部是全能工的SPS 构建问题,即工人具有不同的技能组合和技能水平;2)本文提出的SPS 模型是动态可重构的,考虑了Seru 从构建到拆解的全生命周期.本文其余部分组织如下: 第1 节介绍了问题模型和数学模型,第2 节给出了每个阶段的模型性质分析、相应的精确/近似算法以及算法分析,第3 节介绍了实验设计、实验结果以及分析,第4 节给出了本文结论.

1 问题模型

本文抽象出的问题模型包含两个阶段: Seru 构建和Seru 调度,基于此两阶段问题抽象出问题模型.

1.1 问题假设

本文研究的SPS 构建问题假设描述如下:

1) SPS 内工人总数是确定的,所有的工人都是多能工,且存在技能组合和技能水平上的差异.所有工人在同一生产周期内具有同样的初始剩余工作时间.

2)一个订单中只包含一个产品类型,订单的信息(产品类型和需求量)只有在到来时才能被获知.

3)一个Seru 只生产一种产品类型,一种产品类型可以被SPS 中的多个Seru 生产.

4)一个工人可以被分配到多个Seru 中去.

1.2 符号列表

与本文问题相关的符号变量定义如下所示.

1) 索引

w工人索引(w=1,···,W).

i工序索引(i=1,···,I).

c产品类型索引(c=1,···,C).

d订单索引(d=1,···,D).

sSeru 索引(s=1,···,S).

p可供构建Seru 的场地索引(p=1,···,P).

2) 系统变量

Ow工人w能够加工的工序集合.

td订单d的到来时间.

nd订单d的需求量.

Id生产订单d的所需工序集合.

Wd订单d到来时,当前空闲可以参与加工的工人集合.

Sd完成订单d所构建的Seru 集合.

ptsSerus从构建到拆解的存在时间.

ctsSerus完成生产任务拆解的时刻.

3) 决策变量

1.3 图表模型及约束条件

本节对SC 问题和SS 问题分别建模并给出约束条件.

1) 对SC 问题的工人−工序映射步骤建模,这是一个约束满足问题,其模型描述如下.

其中,式(1)表示对于任一订单d,其所需的任一工序i的数量应与该SPS 中所有能加工该工序的工人实际执行工序i的数量相等;式(2)确保分配给任一工人的工作量不会超过该工人初始剩余工作时间;式(3) 表示参与任一订单d生产的任一工人w所参与加工的工序种类不能超过限制.

2) 对SC 问题的工人−Seru 分配步骤建模,其模型描述如下.

定义Ed为加工某一产品类型包含所有可能的加工路径的图,并结合费用流图的基本定义,为Ed在第一道工序前设置虚拟始点,在最后一道工序后设置虚拟终点.如图1 所示,订单1 需要2 道工序,分别是工序1 和工序2,工人1 和工人2 能够加工工序1,工人3 和工人4 能够加工工序2.则所有代表加工路径的虚线、所有工人节点、始点和终点共同构成E1.

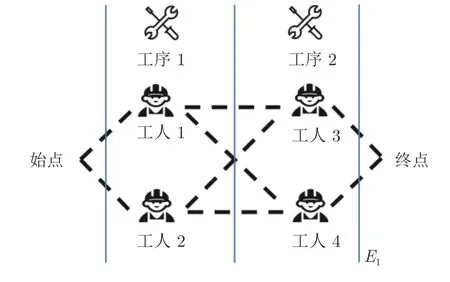
图1 订单1 的潜在加工路径E1Fig.1 Potential processing paths E1 for order 1

对于任一订单d:

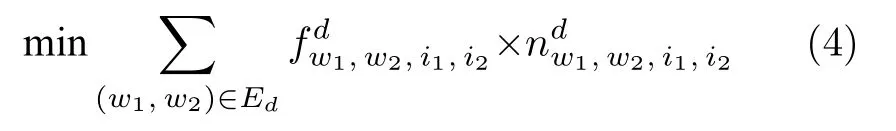
需满足如下约束:

其中,式(4)为该阶段的目标函数,表示通过选择不同的工人构建Seru 从而最小化订单d的所有两两相邻工序之间的单位加工时间之差的绝对值;式(5)和式(6)表示为订单d所构建SPS 的生产量应与订单d的需求量一致;式(7)和式(8)表示工人w1和w2共同生产订单d且工人w1参与的是工序i1生产任务,工人w2参与的是工序i2生产任务,工序i1与工序i2是相邻工序,此时他们的共同生产任务量不能超过第一阶段时所决策出的生产任务量和;式(9)表示产出量必须大于等于0.

对SS 问题建模,其模型描述为

需满足如下约束:

其中,式(10)为该阶段的目标函数,表示最小化该SPS 中Seru 的最大完工时间;式(11)计算的是任一Serus完成其生产任务的最早时刻;式(12)保证需要同一工人参与生产的两个不同Seru 在同一时刻不能同时存在;式(13)保证在任一时刻,一块场地上只能存在一个Seru.

2 模型分析及算法

本节给出SC 问题和SS 问题相关模型性质分析及算法.

对于SC 问题来说,其中涉及到工人−工序映射建立和工人−Seru 分配两个步骤.本节对于这两个步骤分别进行了模型性质分析并给出了精确算法来求解.

定理1.工人−工序映射问题是NP 难的.

证明.本文将经典的NP 难问题——划分问题(Partition problem,PP)[27]归约到建立工人−工序映射问题,从而证明建立工人−工序映射问题也是NP 难问题.

划分问题描述如下: 有一个有限集合U,该集合中每个元素u有一个权重h(u),决策目标是希望找到一个U的子集U′使得

对于任一划分问题的实例,考虑构建如下建立工人−工序映射问题的实例: 目前只有一个订单d到来,其产品类型需要两道工序i1和i2来生产.SPS中共有|U|个工人可以参与加工,且每个工人均有能力加工工序i1和i2. 任一工人w在这两道工序上的单位加工时间为 1 /h(u).对于任一工人来说,参与的工序种类限制=1且初始剩余工作时间为1.订单d的需求量为此时,显然当构建的建立工人−工序映射问题的实例能够求解时,对应的划分问题实例也能得到求解.

由此,建立工人−工序映射是NP 难的. □

定理2.工人−Seru 分配问题可以被多项式时间内求解.

证明.工人−Seru 分配问题模型与最小费用流问题模型是一样的,如图1 所示.最小费用问题是一个可以被多项式时间内求解的经典问题,因此工人−Seru 分配问题也可以被多项式时间内求解.□

推论1.SC 问题是NP 难的.

证明.由定理1 和定理2 可知,SC 问题是NP难的. □

算法 1.SC 算法

步骤 1.初始化每道工序上的工人−工序映射列表,将所有可以加工该道工序的工人放入对应列表中,产品生产量设置为0,设置为0.

步骤 2.工人排序: 对于每道工序,按照单位加工时间非减的顺序对列表进行排序.

步骤 3.依次检验每道工序,若工人−工序映射列表为空,返回False;否则将该工序任务分配给工人−工序映射列表中首个工人,并扣除该工人剩余加工时间,数值为该工人在该道工序上的单位加工时间,对应增加1.

步骤 4.检测至最后一道工序后,产品生产量增加1,若产品生产量小于该订单产品需求量,返回步骤 3;否则,记录并输出.

步骤 5.利用网络单纯型法计算工人−Seru 分配,记录并输出

对于SC 算法,其流程中最复杂的算法循环需要先对订单需求量nd进行1 次循环,再对工人数量W进行嵌套的3 次循环,因此SC 算法的时间复杂度为 O (ndW3).

目前已有很多多项式时间算法或求解器可以对最小费用流问题进行求解,网络单纯形法是其中一个常用的算法.因此,SC 算法的步骤 5 采用这一算法对工人−Seru 分配问题进行求解,使用版本为Python 库中NetworkX 内置的网络单纯型法.算法较为经典,因此细节不再赘述.

定理3.Seru 调度问题是NP 难的.

证明.本文将已被证明是NP 难问题的并行多机调度问题(Parallel machine scheduling,PMS)归约到提出的Seru 调度问题.

并行多机调度问题描述如下: 对于给定的一系列任务J={1,···,j,···},任一任务j∈J有相应的到来时间rt(j)、处理时间pt(j)、完工时间ft(j).这些任务可以在M台机器上加工且不允许抢占.决策目标是找出一个调度方案使得最大完工时间最小.

任一并行多机调度问题实例等同于如下Seru调度问题实例:

令td=rt(j),pts=pt(j),cts=ft(j),显然当Seru 调度问题的实例可以被求解时,对应的并行多机调度问题实例也可以被求解.因此,Seru 调度问题是NP 难的. □

针对这一NP 难的Seru 调度问题,本文提出了近似算法如下:

算法2.SS 算法

步骤 1.初始化: 将所有待调度Seru 放入未调度列表,将已调度列表设置为空,将时刻设置为0.

步骤 2.当未调度列表不为空时,按照pts非增原则对未调度列表中Seru 进行排序;否则,跳至步骤 6.

步骤 3.若存在n个空闲场地,则将未调度列表中前n位的Seru 从未调度列表移动至已调度列表.

步骤 4.对新放入已调度列表中的n个Seru 进行检测,若与其他任一已调度列表中Seru 存在工人占用,则将其重新移动至未调度列表.完成对n个Seru 的检测和操作后,将时刻增加1.

步骤 5.如果有新的Seru 需要被调度,则添加其至未调度列表,检测并移除已调度列表中所有完成加工任务的Seru,返回步骤 2.

步骤 6.停止,输出结果.

对于SS 算法,其流程中最复杂的算法循环需要对Seru 的数目S进行2 次循环,因此SS 算法的时间复杂度为 O (S2).

定理4.SS 算法的近似比为3.

证明.首先,定义最优Makespan为,定义为SS算法得出的生产过程中由于工人占用所造成的Seru 之间非并行的等待时间之和.对于所有已构建的Seru 来说,有3 个非常简单的下界:

由此,得证Seru 调度算法的近似比为3. □

3 实验与分析

为了检验SPS 的性能表现,本文进行了多组实验,波动市场采用不同的参数组合来模拟.仿真实验采用Python 语言实现,运行在3.10 GHz Core i5-2400 CPU,4 GB RAM 的PC 机上.共有3750组用例被测试.以下分别介绍实验设计、算例展示、实验结果和相关分析.

3.1 实验设计

本文中,通过对多样的产品类型和波动变化的需求量两个维度来对波动市场进行描述.具体来说,每种产品的生产需要多道工序,因此设置了不同复杂程度的产品类型组合以不同的级别表示来区分,分别为1,3,5,7,9.每个级别表示该测试用例下到来的多个订单所包含的不同产品类型数量上限.每个测试用例实际生成的产品类型数量采用范围为从1 到该级别数值的均匀分布来生成.每个订单的需求量服从截断正态分布,平均值μ以及波动系数cf=σ/µ用于体现市场波动.μ设置为: 10,20,30,40,50,cf设置为: 0.1,0.3,0.5,0.7,0.9.对于上述波动市场的参数设置如表1 所示.

表1 波动市场的参数描述Table 1 Parameters of volatile markets

工人的技能设置采用Chaining strategy 的方式来设置[28].本实验的其余参数设定如表2 所示.

表2 算例的其余参数描述Table 2 Parameters of test problems

因此,共有5 (产品类型级别)×5 (μ)×5 (cf)=125 组不同参数组合产生,依据中心极限定理[29],每个参数组合下产生30 个算例,因此共有3750 个算例被测试.

3.2 算例展示

为了更清晰地展示模型性质,本节选取一个简单的包含5 个工人的SPS 构建算例来展示.其中,所有工人的初始剩余加工时间均为200,工人在不同工序上的单位加工时间如表3 所示,该生产周期内的订单信息如表4 所示,工人在不同工序上的加工优先次序为单位加工时间短的工人排列在前.

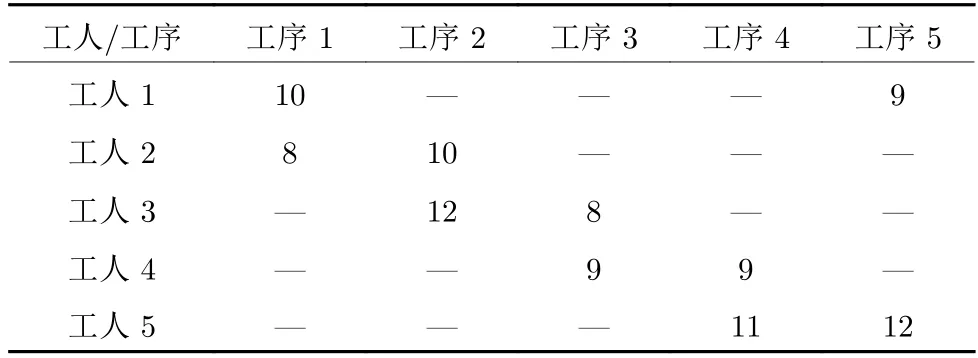
表3 工人在不同工序上的单位加工时间Table 3 Processing time of each worker on different operations

表4 订单信息Table 4 The information of orders

具体地,在该算例中共会有2 个订单到来,订单1 会在时刻0 到来,加工该类型产品需要工序1和工序2 工两道工序,其需求量为15,订单2 会在时刻40 到来,加工该类型产品需要工序3,工序4,工序5 三道工序.订单的详细信息在该订单到来时刻才会被工厂获知.通过第1 阶段算法计算可以很容易得出该算例下工人在不同工序上的加工优先次序,如在加工工序1 时,共有工人1 和工人2 可以参与加工,选择优先顺序为优先选择工人2,其次选择工人1.

在决策订单1 的生产任务分配时,工序1 和工序2 均会优先分配给工人2,而工人2 的生产能力不足以完成整个订单1 的生产,因此需要构建多个Seru 来共同完成订单1 的生产.同理,对于生产订单2 的生产,可根据第1 阶段和第2 阶段的算法计算得出所构建Seru 具体信息如表5 所示.具体来说,为生产订单1 构建Seru 1 和Seru 2,其中Seru 1 为只有工人2 参与加工的单人物台,Seru 2 为工人1 和工人3 共同配合加工,工人1 负责工序1,工人3 负责工序2.Seru 1 产出产品11 件,存在时长为198.Seru 2 产出产品4 件,存在时长为58.为生产订单2 构建Seru 3 和Seru 4,其中Seru 3 有工人3,、工人4、工人5 参与加工,工人3 负责工序3,工人4 负责工序4,工人5 负责工序5.Seru 4 有工人4 和工人5 参与加工,工人4 负责工序3 和工序4,工人5 负责工序5.Seru 3 产出产品9 件,存在时长为125.Seru 4 产出产品2 件,存在时长为48.

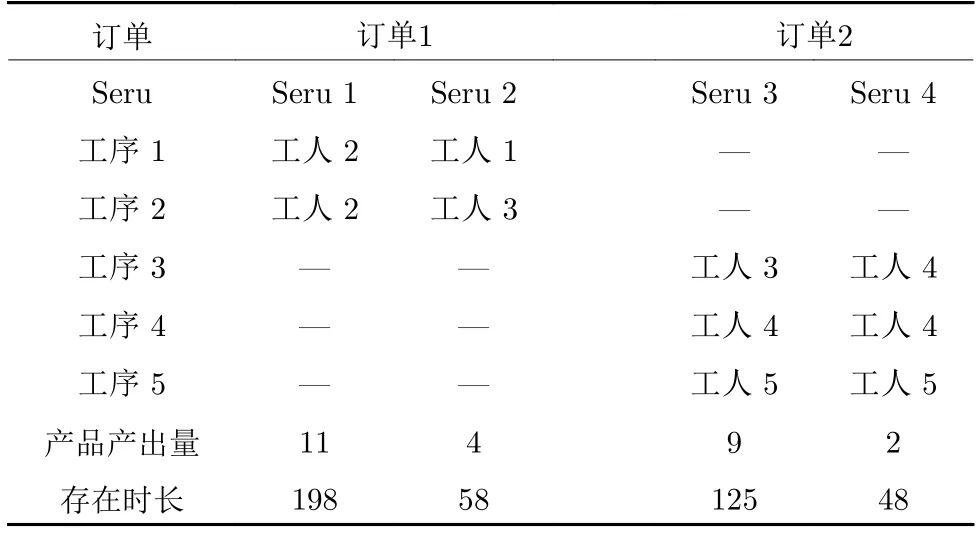
表5 为生产3 个订单所构建的Seru 展示Table 5 Serus that are configured for orders

经第3 阶段算法计算,4 个Seru 的调度结果如图2 所示.Seru 1 和Seru 2 不存在工人占用,可以并行构建.订单2 在时刻40 到来,此时Seru 1 和Seru 2 仍未完成各自生产任务,Seru 2 和Seru 3 均需工人3 参与加工,因此此时Seru 3 不能被构建,先行构建Seru 4.在时刻58,工人完成Seru 2 的生产任务被释放,而Seru 3 和Seru 4 之间有共同需要工人4 和工人5 参与加工,因此Seru 3 仍不能被构建,需等待Seru 4 加工完毕.直到时刻88,Seru 3 可以被构建.

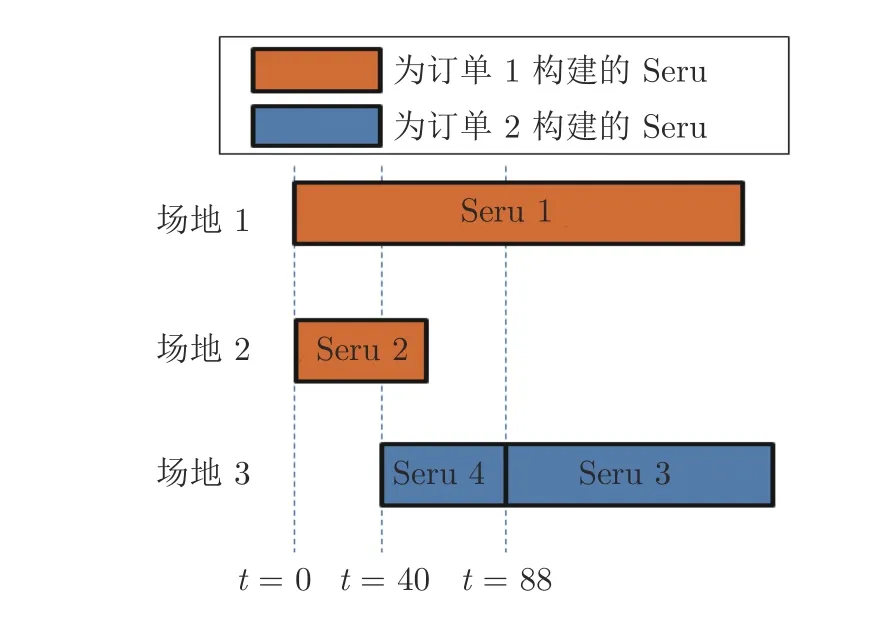
图2 为订单1 和2 所构建的4 个Seru 甘特图Fig.2 Gantt chart for 4 Serus

这个算例展示了Seru 间可能频繁发生的并行构建与工人占用,由此可观察到SPS 具备根据市场变化灵活调整其结构的能力.

3.3 实验结果与分析

本节给出了4 组不同实验的结果展示与分析,分别是: 1) 波动市场环境下,不同的产品类型参数设置对SPS 中Seru 数目、工人利用率、订单完成时间的影响;2)波动市场环境下,不同的产品需求量设置对SPS 中Seru 数目、工人利用率的影响;3) 波动市场环境下,不同的市场波动系数设置对工人利用率的影响.

3.3.1 产品类型参数设置的影响

图3 展示了随着产品类型级别上升,SPS 所构建的Seru 平均数目的变化情况.如图3 所示,当产品类型级别从1 升至9,Seru 平均数目从2.48 上升到了10.62,且整体呈上升趋势.图4 展示了随着产品类型级别上升,工人平均利用率的变化情况.如图3 所示,随着产品类型级别从1 升至9,工人利用率在79.20%和85.14%之间波动,基本趋于稳定.图3 和图4 体现了SPS 在应对同一生产周期内到来的产品类型多样的订单时,为了高效完成生产任务(如维持较高的工人利用率),可以通过构建和拆解不同数量、结构的Seru 从而动态调整系统整体结构来应对不同的市场环境.这也是SPS 可以快速响应多种不同类型订单的重要原因.

图3 Seru 数目随产品类型级别变化趋势Fig.3 The number of Serus versus product types

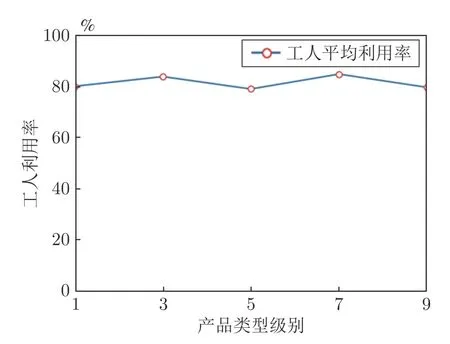
图4 工人利用率随产品类型级别变化趋势Fig.4 The utilization of workers versus product types

图5 展示了Makespan 随着产品类型级别上升的变化情况.可以看到,随着产品类型级别从1 升至9,Makespan 呈整体下降趋势,从2445 下降到了2022.这是一个较为反常的现象,因为随着产品需求种类变多(即产品类型级别上升),一般而言会需要更长的完工时间.通过跟踪实验细节发现,对于产品类型级别较低的测试用例,需要的工序较为单一,从而使得参与加工的工人较为固定,生成的Seru 由于互相之间工人的占用,很难并行构建,因此需要的完工时间较长.而当产品类型级别提高后,产品类型增多,工序种类数目上升,可以参与加工的工人数量也随之上升,这导致了更多的Seru 可以被构建且互相之间发生工人占用情况的概率下降,因此SPS 整体并行性得到了提高,从而获得了更短的Makespan.

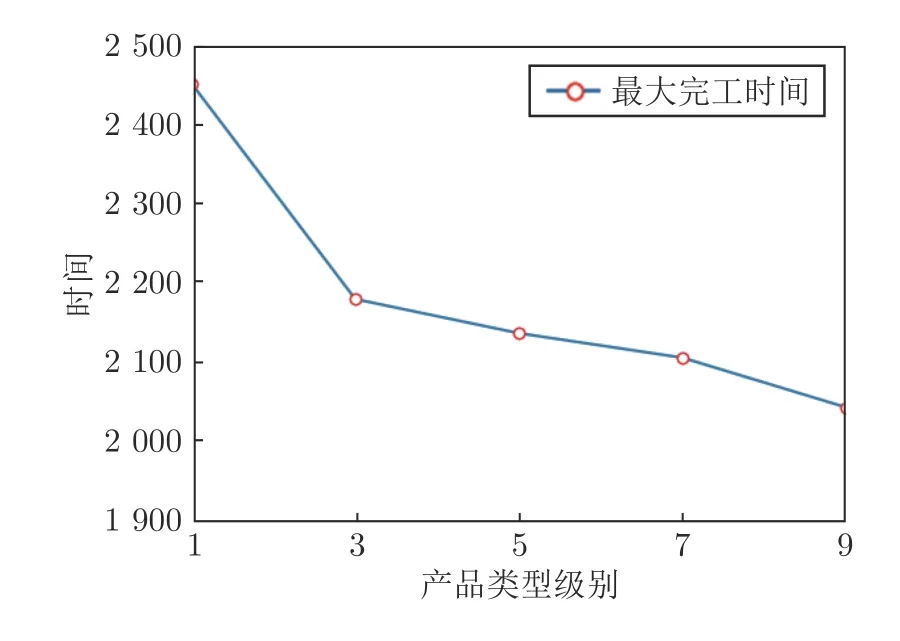
图5 订单最大完工时间随产品类型级别变化趋势Fig.5 The makespan versus product types

3.3.2 产品需求量设置的影响

图6 展示了SPS 所构建的Seru 平均数目随着订单需求量均值µ上升的变化情况.在图6 中,随着订单需求量均值µ从10 升至50,Seru 平均数目从10.18 上升到了14.50.图7 展示了工人平均利用率随着订单需求量均值µ上升的变化情况.如图7所示,工人利用率稳定保持在77.16%附近.图6 和图7 相结合体现出,当市场需求上升时,SPS的工人平均利用率仍能保持在稳定的较高水平.

图6 Seru 数目随订单需求量变化趋势Fig.6 The number of Serus versus product volumes

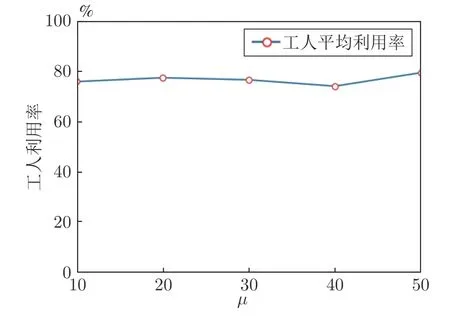
图7 工人利用率随订单需求量变化趋势Fig.7 The utilization of workers versus product types

3.3.3 市场波动系数设置的影响

图8 展示了工人平均利用率随着市场波动系数cf上升的变化情况.从图8 可以看出,随着cf从0.1升至0.9,工人平均利用率保持在80.61%附近.这一结果体现了随着市场的逐步恶化(市场从稳定到剧烈波动),SPS 可以保持较高的工人平均利用率.

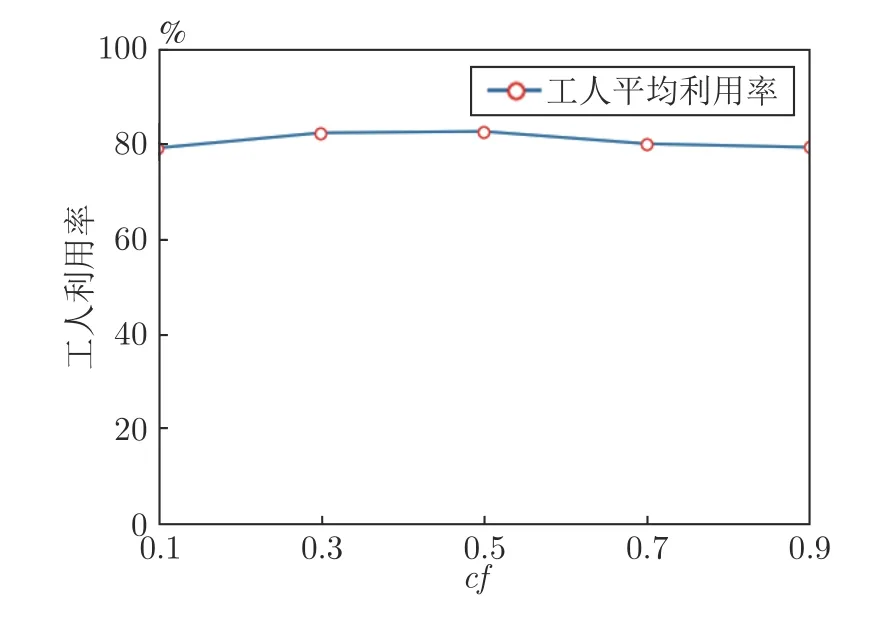
图8 工人利用率随市场波动变化趋势Fig.8 The utilization of workers versus cf levels

以上实验结果验证了面对产品类型多样且产品需求变化大的典型波动市场环境,SPS 具有稳定高效的性能表现,其可重构性使其具有了良好的响应能力.另一方面,在不同参数的设置下,工人利用率始终维持在较高水平,实验结果从侧面验证了所提出模型的有效性.

4 结束语

本文针对波动市场环境下SPS 构建问题,从实际情况出发,考虑了系统中工人是多能工且具有不同的技能组合和技能水平的情况,提出了一种SPS三阶段构建模型与相应方法.构建出的SPS 具有较强的重构能力和良好的响应能力.具体来说,首先,针对当前到来订单中产品的每道工序,为其分配有足够生产能力(具备相应技能和足够的工作时间)的工人;其次,安排不同的工人之间配合来生成Seru,使得工人之间的配合最为平衡,最大化工人利用率;最后,考虑不同Seru 间的工人占用问题,对Seru 进行调度,最小化加权完工时间.在对模型性质分析的基础上,本文提出了相应的精确算法、在线调度算法对模型进行求解.实验结果验证了所构建SPS 的优良性能.

本文所提出的SPS 构建模型和方法具有较强的现实意义.围绕这一研究方向,在今后的工作中,会从以下几个方面进行更深入的探索: 1)考虑更大规模、更为复杂的波动市场环境下SPS 构建问题,设计高效的智能优化算法求解;2)对于生产系统来说,重要的优化指标有很多,比如最大化工人利用率、最小化成本、最小化库存、最小化完工时间等等,考虑建立SPS 构建问题的多目标决策模型及设计相应的多目标优化算法.