射频/直流驱动大气压氩气介质阻挡放电的一维仿真研究*
齐兵 田晓 王静 王屹山2) 司金海 汤洁2)†
1) (中国科学院西安光学精密机械研究所,瞬态光学与光子技术国家重点实验室,西安 710119)
2) (中国科学院大学,北京 100049)
3) (西安交通大学电子科学与工程学院,陕西省信息光子技术重点实验室,西安 710049)
4) (西安科技大学理学院,西安 710054)
5) (西安航空学院理学院,西安 710077)
采用一维自洽耦合流体模型理论研究了射频(rf)/直流(dc)驱动大气压氩气(Ar)介质阻挡放电特性,仿真得到了不同直流电压下,射频最小维持放电电压变化情况、周期平均电子密度平均值随周期平均气体电压平均值变化情况、电子产生率及电子密度的时空分布.分析表明: 直流电压通过改变介质表面电荷密度来影响气隙电压,从而控制放电过程.直流电压较小时放电被抑制,直流电压较大时放电得以恢复.随着直流电压的增大,射频最小维持放电电压振幅随之呈现先增大后减小的变化趋势.另外,当射频电压振幅高于最小维持放电电压振幅时,射频电源驱动与射频/直流驱动时的气隙电压相同,射频电源控制放电.进一步发现在α模式下,随着直流电压的增大,鞘层逐渐形成,电子产生区域从接地电极附近转变为两侧鞘层和主等离子体区边界处;在 γ 模式下,当射频电压振幅高于最小维持放电电压振幅时,电子产生和分布不受直流电压影响.
1 引言
近年来,大气压气体等离子体技术弥补了真空系统成本高、抽真空时间长、技术难度大的不足[1−3],使样品处理流水线化成为可能.已被应用于聚合物薄膜加工[4]、气体催化[5]、材料表面改性[6]、污染物处理[7]、灭菌[8]等领域,因此,对大气压气体放电特性的研究十分必要.
大气压气体放电多为介质阻挡放电(dielectric barrier discharge,DBD),工作频率大多在千赫兹(kHz)数量级[9],电离度较低.在大气压下,DBD通常为丝状放电.在材料表面加工过程中,放电空间中细丝通道电流密度较高,极易产生材料表面烧蚀,但在稀有气体氛围下,这种情况会得到明显的改善.射频(radio frequency,rf)气体放电大多依赖于低压环境.与直流(direct current,dc)或低频交流放电形式相比,射频放电能以更低的击穿电压产生高密度的等离子体.因而,大气压射频稀有气体DBD 在材料表面改性、薄膜加工等领域有着良好的应用前景.1985 年,Kohler 等[10]首先报道了低压射频电容耦合等离子体(capacitively coupled plasmas,CCP)反应器的性能可以通过在反应器电极上施加辅助直流电源来改善,这种新颖的CCP反应器便迅速引起人们的广泛关注.此后,国内外众多学者对rf/dc 驱动CCP 进行了大量实验和数值仿真研究.Tian 等[11]在低压化学气相沉积制备类金刚石薄膜的过程中,采用在射频电源上施加直流负偏压的方法,有效地控制了放电电极电位,从而改善了薄膜性能.Oyanagi 等[12]利用带有外加直流偏压的射频磁控溅射设备制备二硫化钼(MoS2)薄膜,并利用拉曼光谱研究了薄膜的物理性质,研究发现增大直流偏压有助于改善薄膜质量.Li 等[13]采用双rf/dc 电源驱动甲烷等离子体,在低压系统中沉积氢化非晶碳薄膜,在外加直流偏压为100 V时,薄膜硬度达到最大值,同时获得了最小摩擦系数和最佳耐磨性.解艳凤等[14]在利用rf/dc 电源驱动低压等离子体对聚对苯二甲酸乙二醇酯(polyethylene terephthalate,PET)膜进行表面改性时发现: 脉冲直流偏压改善了膜表面的润湿性,提高了膜表面粗糙程度.Zhang[15]利用一维粒子/蒙特卡罗(particle-in-cell/Monte Carlo collision,PIC/MCC)方法研究了rf/dc 电源驱动低压气体放电的表面充电效应.研究发现: 在负直流电压的作用下,大量高能电子向基片移动使自偏压升高,等离子体密度减小;基片厚度增加后,直流电源作用减弱.Diomede等[16]采用PIC/MCC/流体混合模型,研究了直流偏压下射频连续波和脉冲波低压氢等离子体平行平板电容耦合放电.研究发现: 当直流负偏压作用在连续波等离子体一个电极上时,产生的二次电子撞击衬底的能量分布最高能够达到射频电压峰值与直流偏压绝对值之和;在脉冲波等离子体中,在指定的时间窗口同步施加正直流偏压时,正离子能量分布获得一个与直流偏压能量相当的额外峰值.Radmilović-Radjenović与Radjenović[17]研究了rf/dc 复合电场作用下平行平板电极低压氩气放电,导出了在外加弱直流电场作用下,击穿曲线上的最小值、拐点和转折点对应的射频击穿电压.Kawamura 等[18]在研究rf/dc 电源驱动平板和圆柱形电极低压气体放电过程中发现: 在直流电极附近有一个电子密度可忽略不计的鞘层区域,如果射频功率保持不变,则射频鞘层的电压降与直流电压无关.Wang 等[19]利用一维混合模型模拟rf/dc 电源驱动电容耦合低压氩气放电过程.结果表明: 直流偏压的增大促使更多的高能离子注入直流电极,使直流电极上的离子能量分布向高能方向移动,离子角分布的峰值向小角度方向移动.Kawajiri 等[20]采用简单线性模型进行统计分析,阐明了输入参数及其相互作用对rf/dc 电源驱动低压混合等离子体流中粒子停留时间和平均温度的影响.结果表明: 即使直流电源的功率很小,等离子体特性也会发生显著变化.综上所述,在材料制备和表面改性领域,rf/dc电源驱动的CCP 反应器主要利用直流电源改变电极表面鞘层的电压和宽度,从而增大放电过程中二次电子的密度,以实现等离子体密度的提升.但是,目前rf/dc 电源驱动的CCP 反应器大多依赖于低压气体环境工作,存在成本高、技术难度大等问题.因此,性价比更高且易于实现的大气压rf/dc 电源驱动CCP 反应器有良好的应用前景,对放电特性的研究也十分必要.而且,众所周知,射频CCP 反应器可以在α和γ两种放电模式下工作.α模式下等离子体密度小,但放电稳定.γ模式下等离子体密度大,但放电不稳定,易于转化为电弧放电.直流电源的引入势必对放电模式的转换产生影响,而放电模式决定了等离子体密度大小和放电的稳定性,对于这种影响的研究将有助于准确判断等离子体放电模式.目前对于直流电源电压对放电模式转变影响的研究较少,引起影响的内在物理机制不够清晰.
本文旨在研究大气压rf/dc 电源驱动同轴电极氩气介质阻挡放电特性,系统地探究直流电压对射频放电的影响,充分揭示直流电源对放电模式转变影响的内在因素.研究对于深入理解复合电源驱动等离子体放电机理起到积极作用,为新材料制备和材料表面改性高效率工作时的参数调控提供可靠的理论依据.
2 仿真模型
2.1 电极结构
本文放电电极结构和网格剖分情况如图1(a)和图1(b)所示.在大气压氩气中,气体间隙宽度为2—8 mm 时较容易实现稳定放电[21].同轴内电极半径r1为2 mm,外电极半径r2为5 mm,外电极表面覆盖阻挡介质材料厚度dk为1 mm,气体间隙宽度rg为2 mm.外电极施加电压Vs=Vrfsin(2πfrft)+Vdc,Vrf为射频电压振幅,frf为射频频率,Vdc为直流电压.本文采用有限元法,利用射频瞬态求解器对模型进行仿真计算.气体间隙及介质径向剖分单元数分别为200 和30,单元大小比分别为5∶1 和1∶1,在介质表面及接地电极附近剖分单元较小,网格较密集.
2.2 理论模型
本文讨论过程中,假设放电沿轴向是均匀的,且轴向长度远大于气体间隙宽度,建立一维自洽耦合流体模型.模型中考虑四种粒子: 电子e、原子离子Ar+、分子离子、激发态粒子Ar*(4s 能级激发态).激发态粒子包括亚稳态和共振态两种粒子,由于这两种粒子能级接近,故把两种粒子统一为一种考虑[22].描述各粒子输运的连续性方程为[23]
其中n是粒子密度,Γ是粒子通量,S是产生和损失的粒子源项.
在迁移扩散近似下:
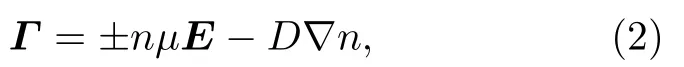
其中E是电场;µ和D分别是粒子的迁移率和扩散系数,正负号分别对应正负电荷.
电子能量方程为

加热项H的计算如下:
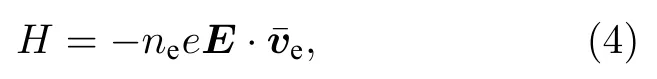
其中e为电子电荷,是电子的平均速度.
能量损失计算如下:
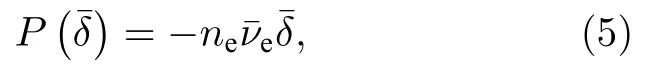
式中,是电子能量转移频率.
电子平均能量通量计算如下:
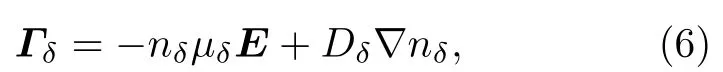
式中,µδ=(5/3)µe为电子能量迁移率,其中µe为电子迁移率;Dδ=(5/3)De为电子能量扩散系数,其中De为电子扩散系数.
电场可在泊松方程中求解:

其中V为电位,ni是离子密度.
2.3 边界条件
对于本文所涉及的一维自洽耦合流体模型,边界条件的确定既要考虑到粒子与界面的相互作用,又要兼顾模型所描述的放电物理过程的合理性.由迁移扩散近似下的粒子通量计算公式(2)可得离子边界条件为
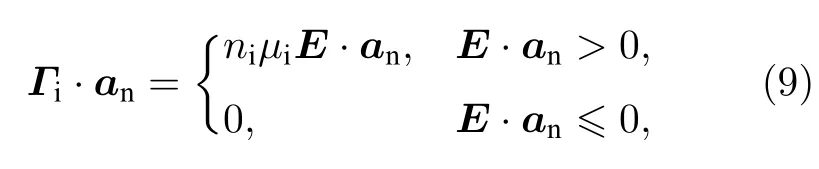
其中Γi为边界处离子通量,an为指向边界方向的单位矢量,µi为离子迁移率.此处假设离子通量仅由从气体间隙向边界的离子迁移提供.
电子边界条件的选取不仅考虑到了迁移和扩散导致界面上电子通量的变化,同时兼顾到了离子轰击边界表面时的二次电子发射:
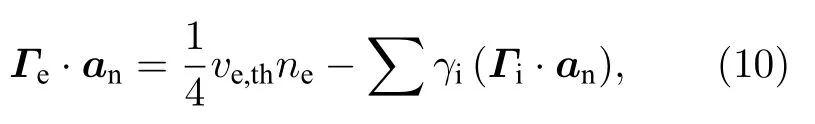
其中Γe为电子通量,ve,th为电子的热速度,γi为二次电子发射系数.
对于中性粒子,吸附系数取最大值,因此边界处通量为0:

另外,本文的模型放电过程中,带电粒子会在介质与气体之间的边界面上累积,这会使该界面两侧的电场出现不连续的情况,根据高斯定理:
其中D1=ε0εrE1为介质在边界处的电位移矢量,D2=ε0E2为气体间隙在边界处的电位移矢量,σ为表面电荷密度.
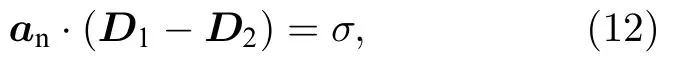
rf/dc 电源接在外电极上,内电极接地,电势边界条件为
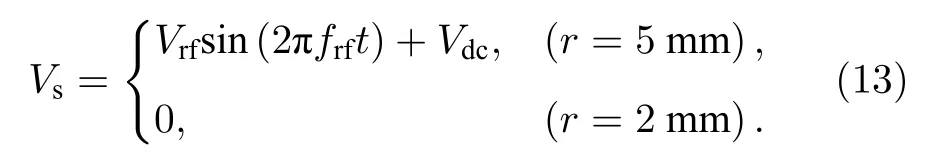
3 仿真结果与讨论
阻挡介质介电常数ε1=ε0εr,ε0为真空介电常数,相对介电常数εr=4.7.射频频率frf为13.56 MHz,气压保持一个标准大气压,气体温度为300 K,二次电子发射系数为0.1[24].电子和Ar+初始密度为1013m–3,其他粒子初始密度为0[22].离子迁移率依据约化电场计算,扩散系数由爱因斯坦关系式获得[25].表1 为本文所涉及的化学反应,包含5 种物质和8 种反应[26],NA为阿伏伽德罗常数,Te为电子温度.反应系数是利用Boltzmann 方程求解器BOLSIG+和文献[27,28]获得.

表1 本文放电模型中所涉及的化学反应Table 1.Chemical reaction formulas used in the discharge model.
3.1 直流电压对放电模式转变的影响
本文仿真计算时间为1000 个射频周期(Trf),此时计算结果已达到稳态.在不同的射频和直流电压下,放电参数时域波形变化如图2(a)—(k)所示.如图2(a),当直流电压Vdc为0 V 时,DBD 射频最小维持放电电压振幅Vrf,min为55 V.因为射频电源频率较高,离子相对于时变瞬时场有相位延迟,所以能够到达介质表面的离子很少;而电子迁移率远超离子[29],因此介质表面累积的电子比离子更多.然而电子的数量(介质表面电荷密度σ较小)不足以对气隙电压Vg产生较大影响,因此受电源电压VS影响,气隙电压Vg保持与VS接近.从图2(b)可以看出,当直流电压Vdc变为–100 V,射频电压振幅Vrf保持55 V 不变时,电源电压在–155 到–45 V 之间振荡变化.仿真计算初始阶段,气隙电压Vg与电源电压VS接近,保持为负值,气隙中的电子在电场的作用下向接地电极移动并在接地电极附近累积.当气隙电压Vg达到负的最大值时气隙间电场最强,电离现象显著,且电离主要在接地电极附近发生.因为电离只在后半个射频周期发生且电离区域较小,从而带电粒子产生速率远小于消耗速率,电离最终无法维持,导致气体间隙中的离子密度始终很小,因此介质表面累积的离子数量很少,不足以对气隙电压Vg产生较大的影响.Vg在–144 到–41 V 之间振荡变化,与电源电压VS变化范围接近.Lisovsikiy 等[30]在低压条件下采用rf/dc 电源驱动氮气,观察到在α模式下,当直流电压增大到一定值时,放电终止,这与本文通过以上分析得到的结论一致.
如图2(c)所示,当直流电压Vdc为–100 V 时,射频最小维持放电电压振幅Vrf,min为273 V.从图2(c)可以发现,此时介质表面电荷密度σ(离子密度)有了明显提升,受其影响气隙电压Vg在–173到230 V 之间振荡变化,而电源电压VS变化范围为–373 至173 V.观察图2(d)可发现,当直流电压Vdc变为–200 V,射频电压振幅Vrf保持273 V不变时,电源电压VS变化范围为–473 到73 V,与图2(b)的分析同理,此时由于电离无法维持导致气隙间离子密度很低,所以介质表面累积的离子数量有限,难以对气隙电压Vg产生较大的影响,Vg在–429 到80 V 之间振荡变化.如图2(e)所示,当直流电压Vdc为–200 V 时,射频最小维持放电电压振幅Vrf,min为318 V.当直流电压Vdc变化至–300 V,射频电压振幅Vrf保持318 V 不变时,如图2(f)所示,电源电压VS在–618 到18 V 之间振荡变化.从图2(f)可发现,随着介质表面电荷密度的大幅提升,气隙电压Vg在–215 到228 V 间振荡变化,在此气隙电压所产生的振荡电场的作用下,放电仍可维持.当Vdc为–300 V 时,如图2(g)所示,Vrf,min为307 V,与Vdc为–200 V 时相比较,Vrf,min略有下降.当Vdc变为–400 V,Vrf保持307 V 不变时,介质表面电荷密度进一步提升,受其影响气隙电压Vg在–205 到230 V 之间振荡变化,如图2(h)所示,气隙电压Vg仍可维持放电.如图2(i)所示,Vdc为–400 V 时,Vrf,min为220 V.如图2(j)所示,Vdc变为–500 V,Vrf保持220 V 不变时,气隙电压Vg变化范围为–129 到209 V,气隙电压Vg仍可维持放电,此时电源电压VS在–720 到–280 V之间振荡变化.如图2(k)所示,Vdc为–500 V 时,Vrf,min为77 V.
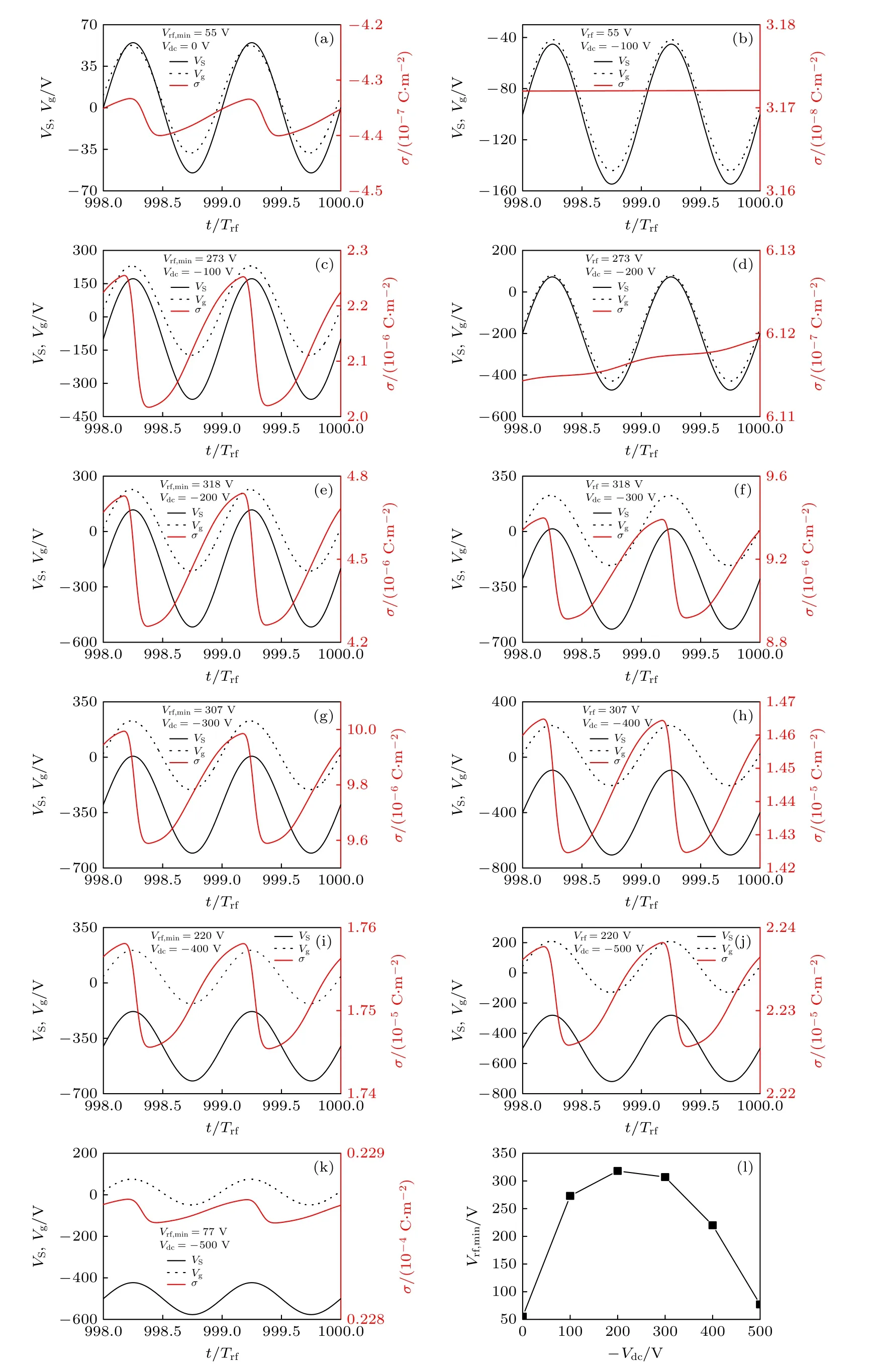
图2 (a)—(k) DBD 放电参数时域波形;(l) 射频最小维持放电电压振幅随直流电压的变化曲线Fig.2.(a)–(k) Time domain waveform of DBD discharge parameters;(l) variation of rf minimum sustaining discharge voltage amplitude with dc voltage.
根据以上分析可知,直流电压通过改变介质表面电荷密度而影响气隙电压Vg,从而控制放电过程.射频最小维持放电电压振幅Vrf,min随直流电压Vdc的增大而先增大后减小,如图2(l).原因是直流电压较小时,气隙电压为负值比正值的持续时间长得多,导致电子集中分布在接地电极附近,所以电离仅在较小的区域内发生,而且主要在射频后半周期发生,使得带电粒子的产生速率远小于消耗速率从而引起放电终止,因此需提高射频电压以维持放电;直流电压较大时,介质表面离子密度的提升使气隙电压为负值和正值的持续时间相差不多,电离增强,因此较小的射频电压即可维持放电.Lisovsikiy 等[30]研究低压条件下rf/dc 复合电场驱动氮气放电模式时发现: 在α模式下,射频电压较小时,放电熄灭的直流电压也很小,而随着直流电压的增大,放电得以恢复,该实验结论与本文以上分析所得结论相似.
图3(a)—(f)显示了不同直流电压Vdc下,周期平均电子密度平均值随周期平均气体电压平均值的变化,曲线起点横坐标对应相应直流电压下射频最小维持放电电压振幅Vrf,min.本文中的“周期平均”是指物理量在一个射频周期内的平均,平均值为气体间隙内的平均值.如图3(a)所示,Vdc为0 V 时,可明显看到两个斜率符号不同的阶段,曲线的斜率即微分电导率在达到89.9 V时改变符号.当低于89.9 V 时,随着的升高而线性增加,等离子体的微分电导率为正且相当恒定,这是α模式放电的典型特征[31].微分电导率在达到89.9 V 时改变符号,此后,随的升高而减小,放电转变为γ模式.对比图3(b)—(f)可以发现,直流电源的引入仅改变了曲线的起点,即射频最小维持放电电压振幅Vrf,min.当Vdc为0,–100,–400 和–500 V 时,存在α和γ两种放电模式,当Vdc为–200 和–300 V 时,仅存在γ模式.从图3(g)可以看出,当Vrf≥Vrf,min时,各直流电压下的曲线几乎重合,这说明当达到或超过Vrf,min后,射频电源控制放电.原因是当达到射频最小维持电压振幅时,介质表面累积的离子使气隙电压时域波形整体向上“平移”,从而单独射频电源驱动与射频/直流驱动时的气隙电压相同;若继续增大射频电压,由于离子相对于时变瞬时电场的相位延迟导致能够到达介质表面的离子很少,因此介质表面离子数量保持基本稳定,射频电源仍控制放电.
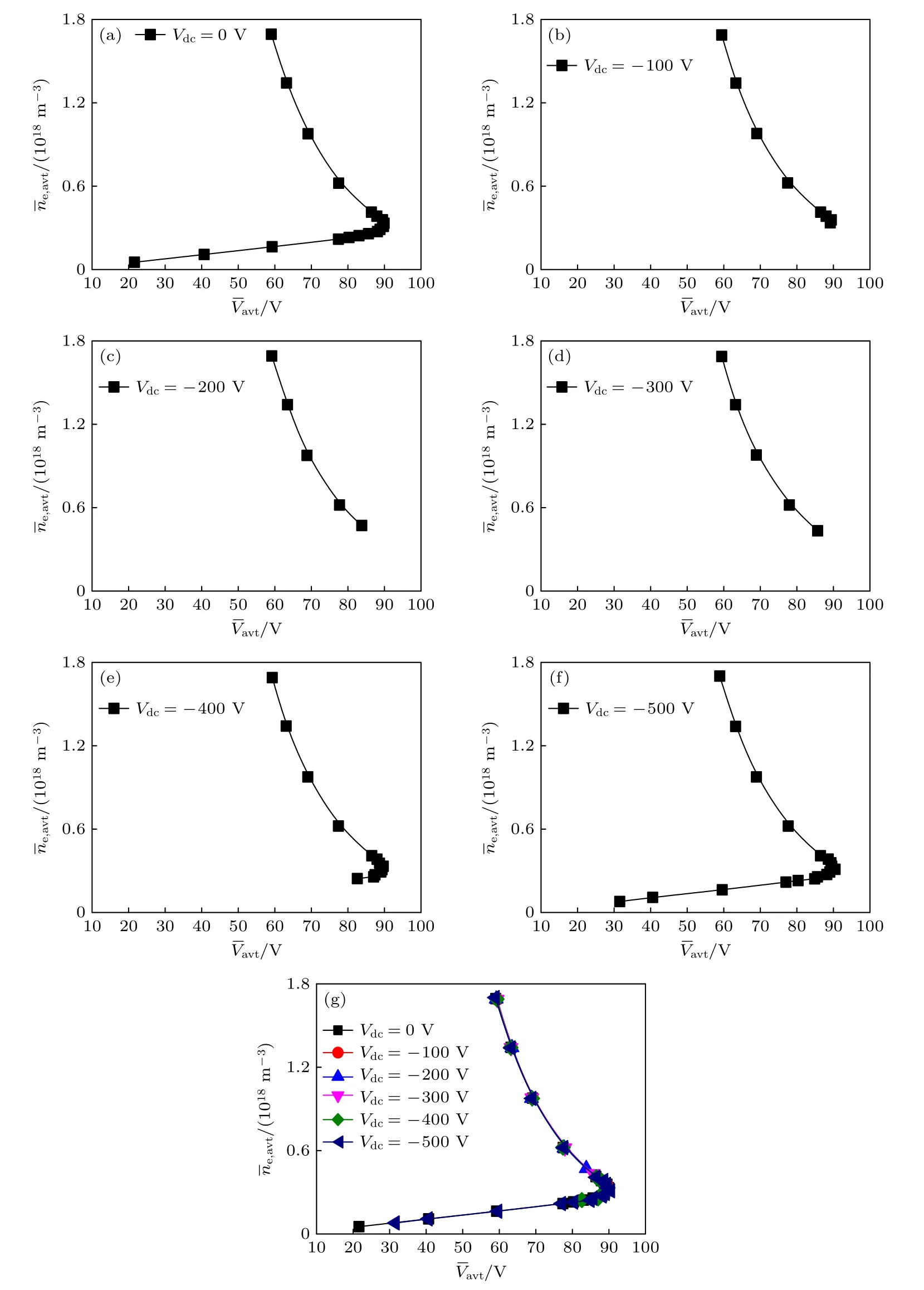
图3 不同直流电压下,周期平均电子密度平均值随周期平均气体电压平均值的变化 (a) 0 V;(b)–100 V;(c)–200 V;(d)–300 V;(e)–400 V;(f)–500 V;(g) 0—–500 VFig.3.Average value of period average electron density varying with the average value of period average gas voltage with different voltage: (a) 0 V;(b)–100 V;(c)–200 V;(d)–300 V;(e)–400 V;(f)–500 V;(g) 0−–500 V.
3.2 直流电压对电子的产生和分布的影响
图4(a)—(f)显示了Vrf为55 V 时,不同直流电压Vdc下,五个射频周期内电子产生率Re(m–3·s–1)的时空分布情况.如图4(a)所示,当Vdc为0 V 时,放电为α模式,从主等离子体区释放到接地电极以及介质的电子被反射到鞘层中并被鞘层电场加速,在鞘层和主等离子体区边界处发生电离倍增,因此大部分电子的产生沿鞘层与主等离子体区边界过渡方向分布[32].在整个射频周期内,该边界附近区域持续电离产生电子.因为高能电子密度会随时空变量变化,所以电离速率也会随之变化,鞘层扩张时电场更强,产生的高能电子密度更高,因此电离现象显著,Re更大.
Vdc分别为–100,–200,–300 和–400 V 时,电子产生率时空分布如图4(b)—(e)所示,由3.1 节的分析可知,气隙电压Vg达到负最大值时气隙间电场最强,电离现象显著,所以Re更大.气隙电压始终为负值,电子在电场的作用下向接地电极移动并在接地电极附近累积,所以电离主要在接地电极附近发生.由于电离只在后半个射频周期发生,从而带电粒子产生速率远小于消耗速率,所以电子密度始终较低,导致Vdc分别为–100,–200,–300 和–400 V 时的电子产生率Re比Vdc为0 V时低得多.
Vdc为–500 V 时,电源电压VS在–555 到–445 V之间振荡变化.在仿真计算的初始阶段,受电源电压VS影响,气隙电压Vg保持与电源电压接近.受较高的气隙电压的影响,初始阶段产生的高能电子较多,电离显著,从而产生了大量的离子,离子在电场的作用下向介质表面运动并在介质表面累积.随着介质表面累积的离子数量的增加,气隙电压Vg发生了显著变化,变为从–105 到–6 V 振荡变化.此时虽然气隙电压Vg仍始终为负值,但是与初始阶段相比带电粒子产生速率已有了明显提升,当电离倍增产生的带电粒子足够多时,气体间隙内的正空间电荷形成鞘层并收缩到能够维持放电的最佳值,两个鞘层之间的区域会形成电子密度恒定的主等离子体区.鞘层形成后,放电主要依靠鞘层电场加速电子与中性粒子碰撞电离维持.Vdc为–500 V时,等离子体密度较低,导致形成的鞘层振荡电场比Vdc为0 V 时小得多,所以如图4(f)所示,Re较小.根据以上分析可以得到如图4(g)所示各直流电压下周期平均电子密度ne,avt径向分布情况.
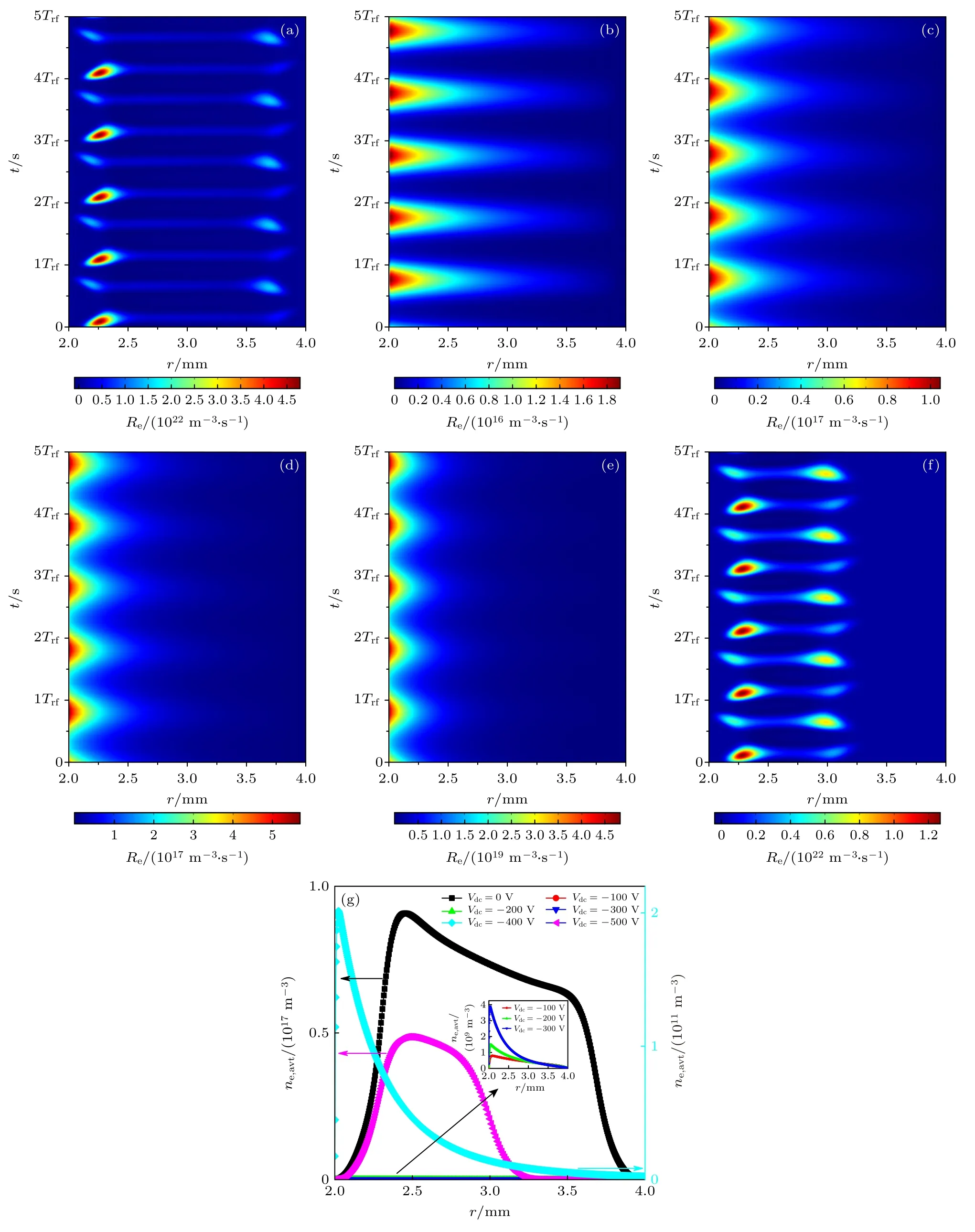
图4 Vrf=55 V 条件下,直流电压为(a) 0,(b)–100,(c)–200,(d)–300,(e)–400 和(f)–500 V 时,电子产生率时空分布;(g) 周期平均电子密度径向分布Fig.4.Under the condition of Vrf=55 V,spatial-temporal distribution of electron generation rate at different dc voltage of (a) 0,(b)–100,(c)–200,(d)–300,(e)–400 and (f)–500 V;(g) radial distribution of period average electron density.
综上所述,在α模式下,当直流电压较小时,放电终止,随着直流电压的进一步增大,放电得以恢复.Lisovsikiy 等[30]在低压条件下利用rf/dc 电源驱动氮气,研究结果表明: 在α模式下,当直流电压增大到一定值时,放电终止,随着直流电压的进一步增大,放电得以恢复,该实验结论与本文以上仿真计算分析得到的结论一致.
Vrf为500 V 时,不同直流电压Vdc下,五个射频周期内电子产生率Re(m–3·s–1)时空分布情况如图5(a)—(f) 所示.当Vdc为0 V 时,放电为γ模式,如图5(a),正空间电荷相当多的鞘层收缩到自我维持的最佳值,因此电离效率比α模式更高,从而Re更大[24].当Vrf≥Vrf,min时,射频电源控制放电.Vdc为–100,–200,–300,–400 和–500 V 时,Vrf,min分别为273,318,307,220 和77 V,均小于500 V,所以如图5(b)—(g)所示,电子产生率时空分布和周期平均电子密度径向分布与Vdc为0 V时几乎相同.综合以上分析可知,放电为γ模式时,在不同的直流电压下,当Vrf≥Vrf,min时,电子的产生和分布不受直流电压影响.在3.3 和3.4 节分析直流电压对电子温度和流向介质表面的电子传导电流密度影响的过程中,考虑到γ模式时,Vrf较高,一般情况下满足Vrf≥Vrf,min,即射频电源控制放电,直流电压对放电的影响很小,所以仅计算了直流电压影响较大的α模式.
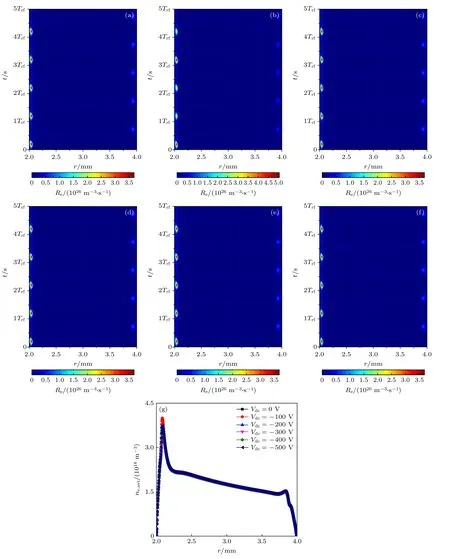
图5 Vrf=500 V 条件下,直流电压分别为(a) 0,(b)–100,(c)–200,(d)–300,(e)–400 和(f)–500 V 时,电子产生率时空分布;(g) 周期平均电子密度径向分布Fig.5.Under the condition of Vrf=500 V,spatial-temporal distribution of electron generation rate with dc voltage of (a) 0,(b)–100,(c)–200,(d)–300,(e)–400 and (f)–500 V;(g) radial distribution of period average electron density.
3.3 直流电压对电子温度分布的影响
碰撞加热和无碰撞加热又称欧姆加热和随机加热,是两种主要的相互竞争的加热机制[32].碰撞加热源于在周期性电场中做振荡运动的电子与中性粒子碰撞发生动量转移,而随机加热源于振荡鞘层向电子的动量传递[33].一般来说,它们与可控放电参数有着密不可分的关系,对于单位面积的碰撞和无碰撞加热功率Pohm和Pstoc[34]
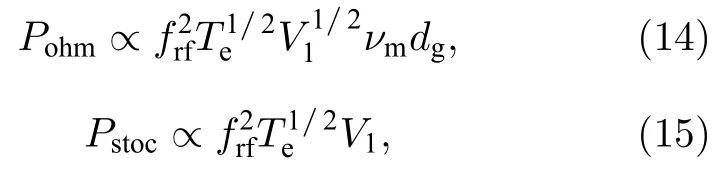
其中,V1是穿过单个鞘层的射频电压;νm为碰撞频率;dg=rg– 2sm,dg是主等离子体区宽度,rg为气体间隙宽度,sm为最大鞘层宽度.
图6 显示了Vrf为55 V 时,不同直流电压下,周期平均电子温度Te,avt空间分布.Vdc为0 V 时,电离主要依靠反射电子在鞘层和主等离子体区边界附近的电离倍增来维持,电离过程的能量损耗能和反射电子的能量损失相平衡,于是主等离子体区的电子温度会下降以防止多余的电离过程发生[35],主等离子体区周期平均电子温度Te,avt约为0.94 eV,而鞘层内Te,avt可达到1.43 eV.Vdc为–100,–200,–300 和–400 V 时,根据3.1 节的分析可知,电离主要在接地电极附近发生,即高能电子主要存在于该区域,因此该区域内电子温度较高,如图6 所示.气隙电压始终为负值,在电场的作用下,介质附近电子密度很低,因此介质附近电子温度很低.气隙中间区域由于没有形成主等离子体区,电子平均能量比Vdc为0 V 时高,故电子温度较高.根据3.2 节电子产生率的分析可知,Vdc为–100,–200,–300和–400 V 时,随着直流电压的增大气隙间电场增强,电离随之增强,所以电子平均能量随直流电压的增大而总体明显提升.根据3.2 节的分析可知Vdc为–500 V 时,等离子体密度比Vdc为0 V 时显著降低,在rf 鞘层内,正空间电荷减少引起鞘层电压随之减小,由(14)式和(15)式可知,rf 鞘层电压减小导致欧姆加热和随机加热功率减小,所以鞘层内电子温度比Vdc为0 V 时小.直流电源的引入使介质附近形成无电子直流鞘层,主等离子体区宽度随之减小,导致欧姆加热功率降低,但随机加热功率不受影响,因此Vdc为–500 V 时主等离子体区电子温度比Vdc为0 V 时略有下降.rf/dc 鞘层的rf 部分正空间电荷密度减小使鞘层电压降低,欧姆加热和随机加热功率降低,但rf/dc 鞘层的dc 部分使一些本应到达介质表面的快速非局域电子返回rf/dc 鞘层,使鞘层电子平均能量增大.此外少量高能二次电子也有助于提高鞘层内的有效电子平均能量,因此,Vdc为–500 V 时的rf/dc 鞘层内电子温度比Vdc为0 V 时显著提高.

图6 不同直流电压下,周期平均电子温度径向分布(Vrf=55 V)Fig.6.Radial distribution of the period average electron temperature with different dc voltages (Vrf=55 V).
3.4 直流电压对流向介质的电子传导电流密度的影响
电容耦合等离子体放电过程中,位移电流是总电流的主体,但由于高能电子能够克服鞘层中的电位降而到达电极,因此流向电极的电子传导电流依然存在[36].Vrf为55 V 时,不同直流电压下一个射频周期内流向介质表面的电子传导电流密度Je时域变化波形如图7(a)所示.由于Ar 等离子体中电子能量较低(3.3 节分析),所以只有当rf/dc 鞘层宽度和电位降很小时,电子才有机会到达介质表面.Vdc为0 V 时,前半个射频周期主要由气隙向介质表面释放电子,后半个射频周期由介质表面向气隙释放电子,由于气隙间电子密度比介质表面电子密度大得多,所以前半个射频周期电子传导电流密度Je比后半个射频周期大得多.而且Vdc为0 V时,等离子体密度最高(3.2 节分析),介质附近鞘层厚度和电位降最小,如图7(b)所示,因此与Vdc为其他值时相比,Je最大.Vdc为–100,–200,–300和–400 V 时,根据3.1 节分析可知,介质附近电子密度很低,导致能够到达介质表面的电子很少,所以Je很小.Vdc为–100 和–200 V 时,Je为负值,即电子传导电流方向由气隙指向介质表面,原因是虽然气隙电压为负值,但电压较小,仍有部分高能电子流向介质表面.Vdc为–300 和–400 V 时,随着气隙电压的增大,气隙间电场增强,电子在电场的作用下从介质表面流向气隙,因此Je始终为正值.Vdc为–500 V 时,鞘层形成,直流电源的引入引起rf/dc 鞘层宽度增大,一些本应到达介质表面的快速非局域电子被反射回鞘层,电子由介质表面流向气隙,所以Je始终为正值.
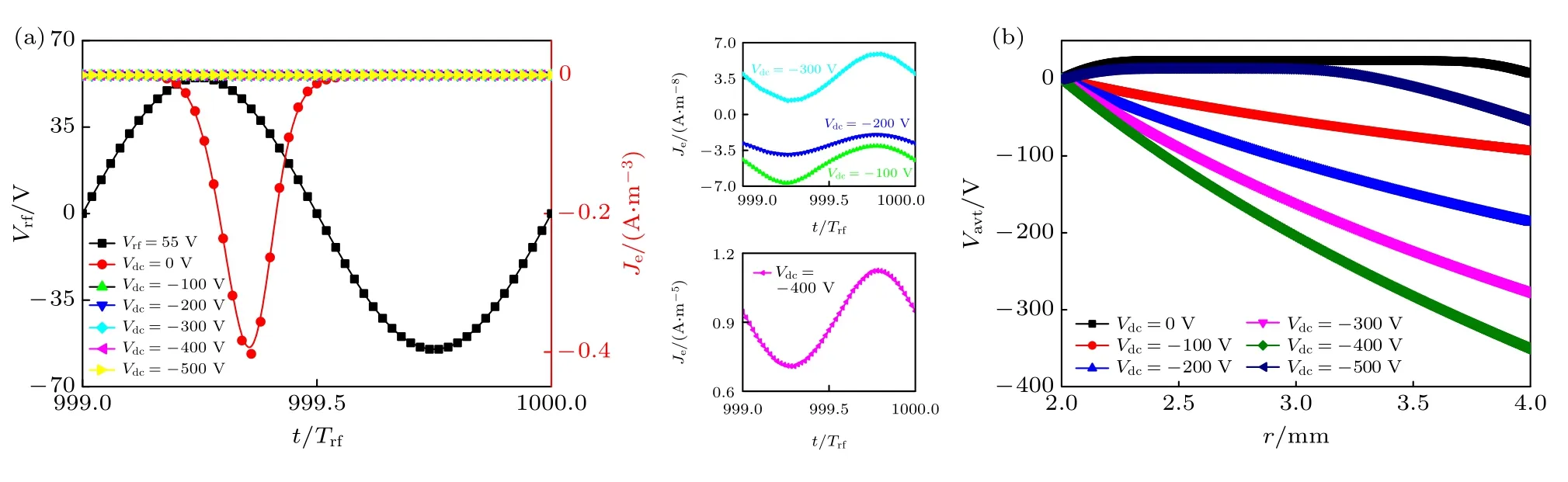
图7 Vrf=55 V 时,不同直流电压下,(a)流向介质表面的电子传导电流密度;(b) 周期平均气体电压径向分布Fig.7.Under different dc voltage and Vrf=55 V,(a) electron conduction current density on dielectric surface;(b) radial distribution of period average gas voltage.
4 结论
本文建立了rf/dc 电源驱动大气压氩气介质阻挡同轴电极自洽耦合一维流体仿真模型,运用有限元法对模型进行了数值求解.通过对介质表面电荷密度随直流电压变化过程的分析表明: 直流电压通过对介质表面电荷密度的调控影响气隙电压,从而控制放电过程.射频最小维持放电电压振幅随直流电压的增大而呈现先增大后减小的变化趋势,当射频电压振幅高于最小维持放电电压振幅时,因为射频电源驱动与射频/直流驱动时的气隙电压相同,所以射频电源控制放电.通过对不同直流电压下电子产生物理过程的分析表明:α模式下,当直流电压较小时,电子主要在接地电极附近产生;而直流电压较大时,鞘层形成,电子主要在两侧鞘层和主等离子体区边界处产生.γ模式下,当射频电压振幅高于最小维持放电电压振幅时,射频电源控制放电,电子产生和分布不受直流电压影响.通过对气隙间周期平均电势径向分布随直流电压变化情况的分析表明:α模式下,当直流电压较小时,气隙间离子密度较低,导致鞘层无法形成,直流电压通过改变气隙间电场强度而影响电子温度分布和流向介质表面的电子传导电流密度;当直流电压较大时,鞘层形成,直流电压通过对鞘层电压和主等离子体区宽度的控制而影响电子温度分布和流向介质表面的电子传导电流密度.
本文的研究有助于加深对复合电源驱动等离子体放电机理的理解,为优化rf/dc 电源驱动介质阻挡CCP 反应器提供有价值的参考.

