BCl3 同位素分离中二聚体的浓度*
李业军 郭静 马俊平 唐显 李鑫 闫冰‡
1) (中国原子能科学研究院同位素研究所,北京 102413)
2) (吉林大学原子与分子物理研究所,长春 130012)
在激光辅助凝聚抑制同位素分离的过冷超饱和超声速气流中,同位素分子BCl3 与载气原子(稀有气体原子RG: He,Ne,Ar,Kr,Xe)间的接触碰撞形成二聚体BCl3:RG,二聚体浓度与温度等参数的关系对同位素分离中参数调控与选择具有重要意义.本文基于分子间相互作用解析势函数,考虑二体、三体碰撞诱导的二聚体缔合与解离,给出了BCl3:RG 二聚体浓度随绝对温度变化的关系.结果表明: 二体碰撞在BCl3:RG 形成中占据主导,在BCl3 初始摩尔分数为0.01—0.10 内,BCl3:RG 二聚体浓度随BCl3 初始摩尔分数变化大致呈线性关系,初始摩尔分数不仅决定理论上二聚体浓度的极限值,还主导了低温区二聚体浓度;在超声速流气室温度为20 K 左右时,采用较重的惰性气体Kr 形成二聚体的浓度最大,同时给出了不同温度区间各种载气对应的二聚体浓度大小;进一步,通过二聚体中有效解离能和伸缩振动频率等参数的变化,在分子尺度上利用简单模型解释了激光辅助凝聚抑制的内在微观机制.
1 引言
激光激发同位素分离(SILEX)法分离同位素是利用激光选择性激发目标同位素分子到振转激发态,降低表面吸附能力,受激的目标同位素分子在超声速分子流中与载气碰撞形成二聚体瞬间解离,非目标同位素分子与载气碰撞以相对稳定二聚体形式存在于超声速分子流中,造成同位素分子间的质量差增大,致使同位素分子沿喷流径向扩散距离差扩大,提高气动喷嘴法分离同位素能力.SILEX方法具有投资少、经济性好等特点,美国已将其规划为第三代铀浓缩技术,SILEX 方法也可以浓缩硼(B)、硅(Si)、碳(C)、钼(Mo)、氯(Cl)、溴(Br)、硫(S)等[1−5]多种同位素.
根据SILEX 浓缩原理,二聚体的形成及动力学行为对SILEX 浓缩效率和产率至关重要.尽管同位素硼等的分离方案研究已经开展[6−10],但在原子分子尺度对其机理的深入研究尚显不足.例如,超声速流工作条件下,即几十开的绝对温度下,二聚体形成的微观动力学机制;二体和三体碰撞过程哪个主导的问题[11,12];二聚体形成浓度与分子尺度物理参数(如相互作用势、分子常数等)和宏观参数(如温度等)的关系等,上述研究在已发表文献中的研究尤其不足,因此本文将系统研究在超声速流下二聚体形成的物理机制,探究与二聚体形成有关的物理参数,揭示同位素分离中二聚体形成的控制因素,并依据研究结果对部分同位素分离工作条件给出建议.所以,首先研究二体、三体碰撞过程对二聚体形成的作用;之后研究不同条件下,不同的载气对于二聚体形成浓度的影响.
本文以BCl3分子与载气原子(具体为稀有气体原子RG: He,Ne,Ar,Kr,Xe)形成的二聚体为具体研究对象,通过原子分子间的相互作用势函数和碰撞参数等,得到BCl3分子参与形成的二聚体浓度与温度的关系等,最后根据研究结果给出理论分析和研究结论.
2 研究方法和计算细节
以BCl3分子与载气原子RG 形成的二聚体为具体研究对象,模拟研究采用Eerkens[12,13]建议的模型.具体的研究方法在文献[6,12,14−19]中已有详细的叙述和发展应用,下面只简单介绍此方法.BCl3分子与载气原子RG 的相互作用势以非简谐的范德瓦耳斯(van der Waals,vdW)势描述,分子间势阱深度为Dα(cm–1),ϵα=hνα为二聚体伸缩振动的基频能量(cm–1,其中να为频率).处于vdW 势阱中二聚体BCl3:RG 由低振动能级跃迁到最高振动能级vd视为二聚体的解离;反之,由vd跃迁到低振动能级视为二聚体缔合形成.由于相互作用势的非简谐性,只有相邻振动能级之间的跃迁才最显著,其他跃迁可忽略,因此只考虑最高振动能级vd与次高振动能级vd–1 之间的跃迁矩阵元.
在此模型下,二聚体的缔合与解离都看作通过原子分子碰撞诱导跃迁发生的动力学过程,对于碰撞引起的跃迁,在模型中只考虑两种碰撞类型.其一是形成二聚体的两个分子(BCl3分子与载气原子RG)之间的直接碰撞形成,即平动能通过二聚体势阱中最高振动能级向下跃迁而释放,从而形成稳定的二聚体;另一种是第三个粒子碰撞二聚体引起的解离与缔合,其中第三个粒子可以是气体中的两种分子之一(BCl3或RG),或是另一个二聚体.碰撞过程由两方面主导,一是宏观碰撞参数,即描述混合气体中两个分子的碰撞发生的概率;另一个是微观的振动能级跃迁,描述两个分子发生碰撞后的量子态的跃迁.
对于给定摩尔分数的混合气体缔合形成的二聚体的粒子数的问题,假定温度为T的混合气体处于动态平衡状态,即气体中二聚体的解离速率与二聚体的缔合形成速率处于稳态:
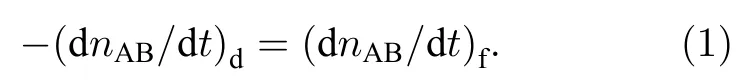
二聚体缔合形成的粒子数速率变化方程为
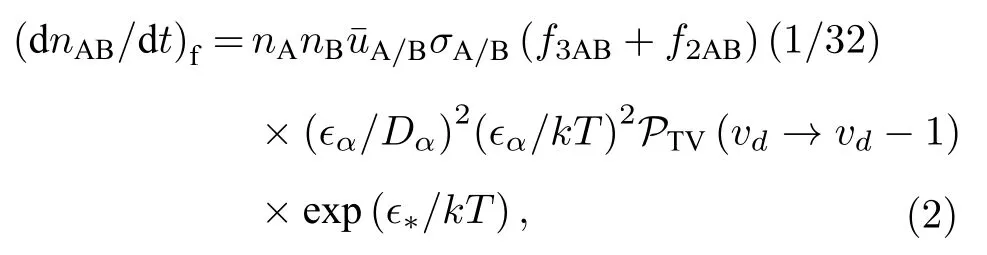
其中,nA,nB和nAB分别为混合气体中A,B 和二聚体AB 的粒子数;σA/B和分别表示A 与B的碰撞截面,A 与B 的相对速度,其中角标表示参与碰撞或相对运动的两类粒子;f2AB和f3AB分别为二体与三体项;k为玻尔兹曼常数;T为绝对温度;PTV(vd →vd −1)表示碰撞诱导(平动-振动)的最高振动能级vd到次高振动能级vd– 1 的跃迁概率;表示此二振动能级的间隔.
碰撞解离的粒子数变化速率表达式为
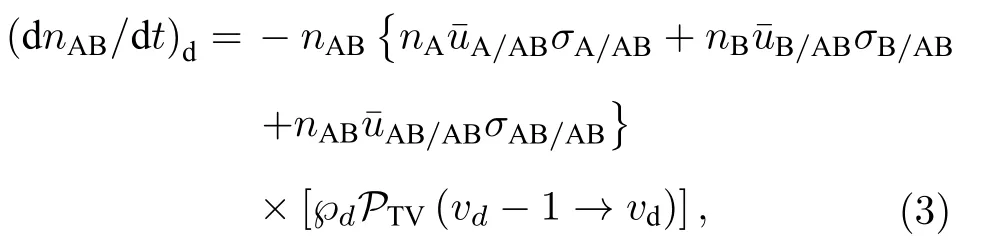
其中,

碰撞诱导跃迁概率与二聚体形成过程相反,PTV(vd −1→vd)为次高能级跃迁到最高能级,其他参数与(1)式相同.利用粒子数平衡条件(1)式,经过推导可给出二聚体浓度表达式.A,B 粒子的摩尔分数yA,yB和二聚体浓度yAB定义为
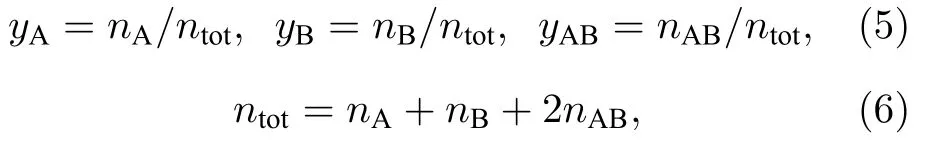
这里,ntot是混合气体中单体分子的总数.
在上述模型和近似下,可导出气体混合物中的二聚体浓度为

其中
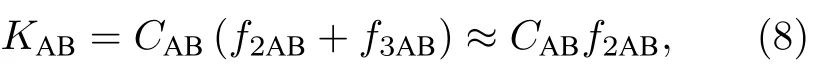
参数CAB定义为
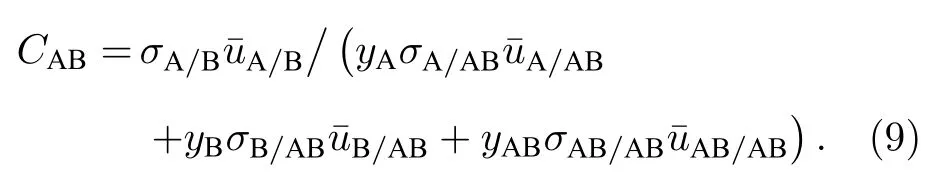
(9)式考虑了A,B 和二聚体AB 参与的碰撞.(8)式忽略三体项f3AB的贡献,略去f3AB具体表达式;与二体项f2AB相比,三体项至少小三个数量级,这两项决定的二聚体浓度的比较见下文研究结果.二体项f2AB的定义为
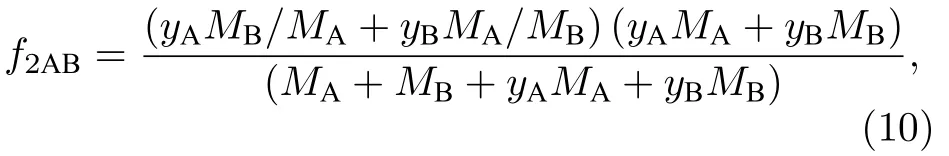
其中,MA,MB为分子A 和B 的质量.
(7)式中的三参数函数g(ϵα,Dα,T)可以简化为双参数函数g(a,b):
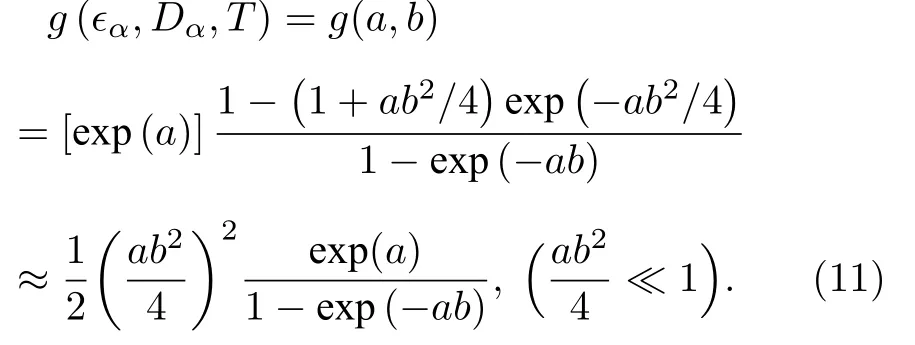
并在ab2/4≪1时,可进一步简化为(11)式,其中a和b分别定义为
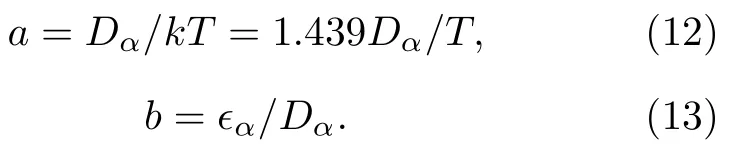
其中以BCl3:Kr 二聚体浓度为例,BCl3的初始摩尔分数取为0.02,Kr 的摩尔分数取为0.98.在此条件下,初始值CAB=0.27915,f2AB=0.4047,则KAB=0.1130.
3 结果和讨论
3.1 BCl3:RG 二聚体形成浓度随温度的变化
利用(8)—(10)式计算出原子分子参数,在BCl3和RG 的初始摩尔分数分别为0.98 和0.02的条件下,首先研究了二体、三体碰撞对二聚体浓度的贡献,结果如图1 所示,三体碰撞对二聚体浓度的贡献比二体贡献小三、四个数量级.在低温条件下,三体碰撞可以看作一个“近似约束”(接触或绕行)的BCl3与RG 组成的BCl3○RG 二体系统被第三个粒子(RG 或BCl3等)碰撞,进而碰撞导致近似束缚的BCl3○RG 二体系统缔合成键或解离为BCl3+RG.气体中的大多数分子碰撞在任何瞬间都是两体碰撞,三体与二体碰撞的比率近似等于两体碰撞散射截面的半径与平均自由程之比,在本文的研究条件下可估计出三体“碰撞事件”要比二体“碰撞事件”小三、四个数量级[12],因此在实际的模拟中可将此部分贡献忽略.
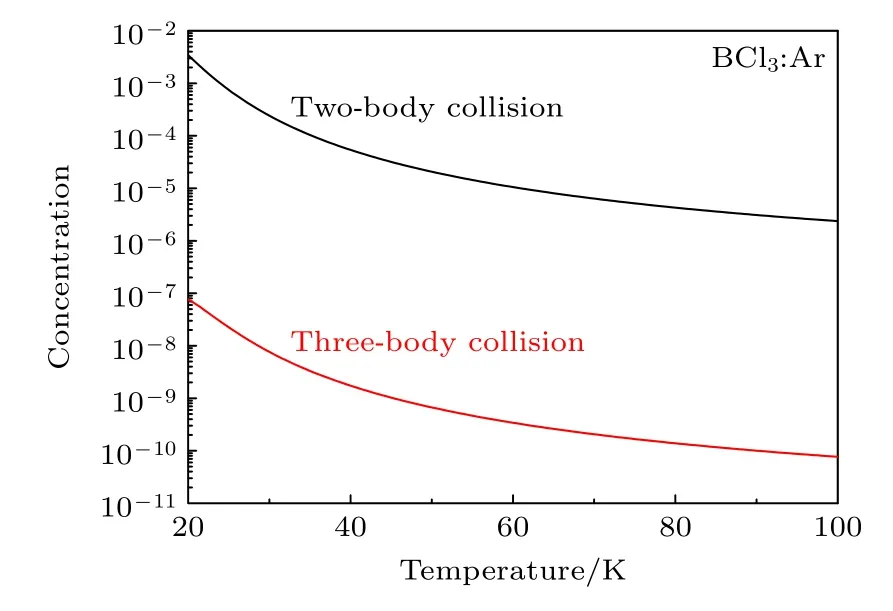
图1 二体、三体碰撞机制对BCl3:Ar 二聚体浓度的贡献Fig.1.Contributions of two-body and three-body collision mechanisms to the dimer concentration of BCl3:Ar.
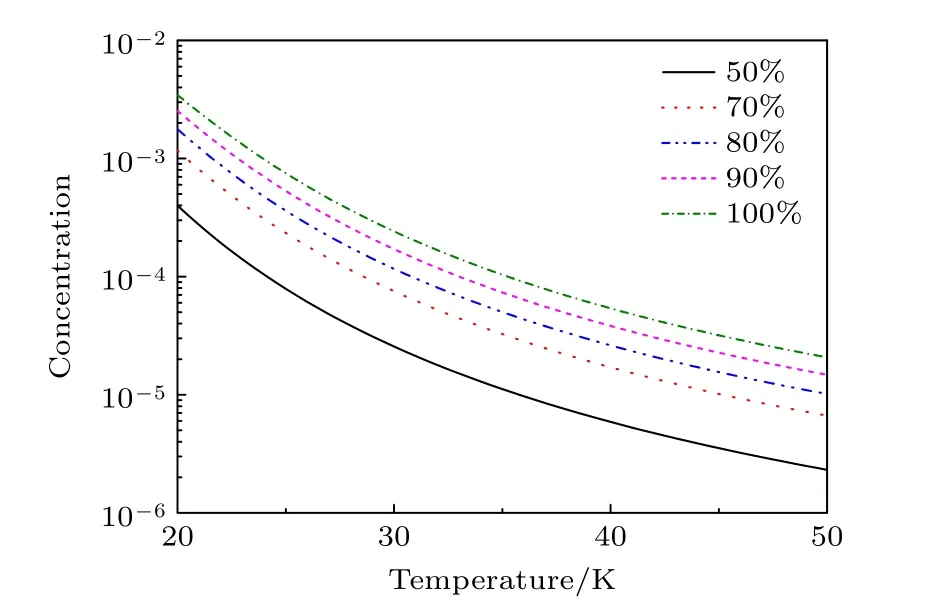
之后,利用(11)式给出了BCl3∶RG 二聚体浓度yAB随绝对温度T的变化关系,并绘于图2 中.我们之前的模拟研究[20,21]表明,BCl3同位素分离的最佳温度为几十开,考虑到同位素分离的实际工作条件,温度范围取为20—40 K.因初始的摩尔分数BCl3为0.02,故而BCl3:RG 二聚体浓度的理论极限为0.02,即绝对零度时所有的BCl3凝聚为二聚体BCl3:RG;随着温度升高,在小于40 K 的范围内,所有二聚体浓度均迅速下降,降至20 K 时的几十到几百分之一.在温度与碰撞能量可比拟时,缔合的概率最大,而随着温度升高,增大的碰撞能量会增加二聚体解离概率,且研究中的温度范围不足以使BCl3发生分子内的振动激发,因此二聚体浓度随温度变化曲线会随着温度增加单调减小.由图2 可知,在绝对温度20 K 时,BCl3:Kr 二聚体浓度最大,接近0.01,为理论极限值的一半;其次为BCl3:Xe 二聚体,浓度为0.0066,约为极限值的1/3;再次为BCl3:Ar二聚体,浓度为0.0034,约为极限值的1/6;浓度最小的二聚体为BCl3:He 和BCl3:Ne,约0.002,为极限值的1/10.在绝对温度20—30 K 之间,与其他二聚体浓度相比,BCl3:Kr二聚体浓度始终最大,但在31 K 时浓度降至20 K时的1/20;在25 K 时,BCl3:Kr 二聚体浓度是其他二聚体浓度的2—4 倍不等.在20—25 K范围内,BCl3:Xe 二聚体浓度仅次于BCl3:Kr,但大于25 K时随着温度下降最快.下面在不同温度范围内,给出浓度最高的三种BCl3:RG 二聚体的RG 原子:20.0 图2 BCl3:RG 二聚体的浓度与温度T 关系Fig.2.Relationships of concentration for BCl3:RG dimer and absolute temperature T. 表1 不同温度(20—40 K)下二聚体浓度(初始摩尔分数比0.02∶0.98)Table 1.Concentration of BCl3:RG at different absolute temperature (20—40 K).Initial mole fractions ration is 0.02∶0.98. 下面讨论初始BCl3气体与载气RG 的摩尔分数对二聚体凝聚浓度影响.以BCl3:Kr 为例,分别给出了BCl3初始摩尔分数(ya0)为0.01,0.02,0.05和0.1 时,二聚体浓度与温度关系,如图3 所示.结果表明,二聚体浓度随初始BCl3摩尔分数增加大致呈线性增加,其原因主要是在我们关注的摩尔分数范围内,原子分子碰撞参数变化不明显,二聚体浓度(7)式中,变化主要由初始摩尔分数变化主导.这一简单结论对实验中二聚体浓度的调节具有应用价值,但需考虑受激分子输运过程中振动-振动能量转移带来的同位素竞争问题. 图3 BCl3 不同初始摩尔分数下BCl3:Kr 浓度与温度的关系Fig.3.Relationships of concentration for BCl3:Kr dimer and absolute temperature with the different initial mole fractions of BCl3. 在激光激发分子分离同位素技术和实验中,采用特定波长,利用不同同位素分子的振动频率不同的特点,选择性激发一种同位素分子,进而造成不同同位素分子的二聚体浓度的较大差异,从而导致同位素体系的较大的质量差异,更有利于同位素的分离.本节旨在研究半定量模拟分子被激光选择性激发时二聚体浓度的变化.在二聚体分子10BCl3:RG和11BCl3:RG 中,基态的BCl3与确定的RG 原子间相互作用势的同位素效应可以忽略;当目标分子被激光选择性激发时,一种同位素分子处于振动激发态,内能增加;与处于振动基态的分子相比,处于振动激发态的分子与其他原子、分子相互作用势能函数参数会发生变化.一般地,当BCl3被激发到振动激发态时,二聚体BCl3:RG 中分子间相互作用会变弱,即有效的解离能DLJ会变小,相应地,BCl3:RG 之间的振动频率να也会减小.在图4 与图5 中,以BCl3:Ar 为例,考查了两个参数变小的情况下,即定性模拟目标分子被选择激发后,二聚体凝聚的浓度变化趋势,并借此分析激光选择性激发下,目标分子形成二聚体浓度的变化.如图4 所示,温度为20 K,且解离能减小10%时,浓度下降约1/3 (3.5‰—2.3‰);解离能减小50%时,浓度下降为原来的约1/7 (3.5‰—0.5‰);并且温度在20—59 K 范围内,随着温度升高,二聚体浓度变化对解离能变化不再敏感.图4 结果表明,在采用SILEX 技术利用BCl3分子分离B 同位素时,为获得显著的二聚体浓度差异,将温度控制在40 K 之内十分重要. 图4 不同解离能DLJ 下BCl3:Ar 浓度与温度的关系Fig.4.Relationships of concentration for BCl3:Ar dimer and absolute temperature with the different dissociation energies DLJ. 图5 不同等效振动频率下BCl3:Ar 浓度与温度关系Fig.5.Relationships of concentration for BCl3:Ar dimer and absolute temperature at different effective vibrational frequency. 图5 中100%表示等效振动频率不变,即BCl3分子未被激发的情况;90%表示BCl3分子被激发后且BCl3分子与RG 之间的伸缩频率缩小10%的情况,其他依此类推.温度为20 K,频率减小10%时,浓度约下降30% (3.5‰—2.5‰);频率减小50%时,浓度下降为原来的约1/9 (3.5‰—0.4‰).可见,在低温20—40 K 范围,浓度变化随着频率改变呈现均匀变化趋势,且呈单调减小趋势.综上所述,当目标分子被选择激发处于振动激发态时,有效的解离能减小,振动频率也变小,在此种情况下,在低温区的二聚体浓度对DLJ和α的变化十分敏感并大幅度单调变小,这是激光激发分离同位素分子方法的分子物理基础.上述结果,从分子尺度微观上解释了SILEX 技术中,可利用激光选择性激发目标同位素分子,提高目标分子的内能,降低其表面吸附系数,从而抑制一种同位素分子的二聚体形成的物理机制. 本文采用非谐势函数描述BCl3与RG 之间的相互作用势,在碰撞诱导二聚体解离与缔合模型下,考虑了二体碰撞缔合和三体碰撞缔合与解离,模拟研究了平衡条件下20—40 K 温度范围内BCl3:RG 二聚体浓度与温度的关系;并给出了下述主要结论. 1) 对二聚体浓度的贡献,三体碰撞概率比二体碰撞概率小三、四个数量级,低温条件下可忽略;在BCl3初始摩尔分数为0.01—0.1 范围内,BCl3:RG二聚体浓度变化随着BCl3初始摩尔分数变化,大致呈线性关系;初始摩尔分数不仅决定二聚体浓度的理论极限,也主导了模型中低温区二聚体浓度. 2) 在低温20—40 K 范围内,考查了惰性气体与BCl3形成二聚体的浓度与绝对温度的关系.结果表明,在超声速流气室温度为20 K 时,研究结果建议采用较重的惰性气体Kr,Xe,Ar 等作为载气,BCl3:Kr 的二聚体浓度最大,是Xe 的3 倍,Ar 的6 倍.低温条件下BCl3:Kr 二聚体浓度最大主要得益于该体系的解离能等相互作用势参数. 3)通过考查在一定范围内势能参数的变化,半定量模拟了BCl3分子在被激光选择性振动激发后二聚体浓度的变化,并利用此简单模型,在分子尺度解释了SILEX 技术中抑制二聚体凝聚的微观机理.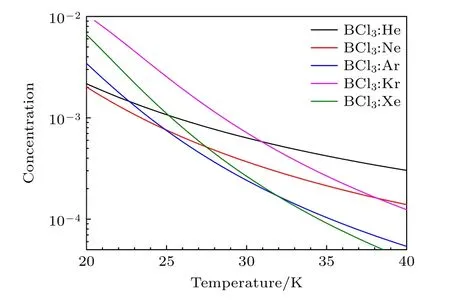

3.2 不同势参数下二聚体浓度与温度的关系

4 结论

