“问题解决”中推理教学的策略——以“两角差的余弦公式”为例*

周文英 (江苏省常熟中学 215516)

在高中数学教学实践中，命题或公式类教学多侧重于结论运用，轻结论探索，而基于“问题解决”的推理教学实践能够弥补这一不足.推理教学实践更为关注结论的由来，强调师生探索结论的过程，且在课堂“教”与“学”的整个环节之中将问题作为中介，连接各个教学环节，将学生置身于问题解决的学习情境之中，不仅强化了学习活动的实践性，同时也使得数学课堂教学更具推理特色.

1 引入问题，建构新课开端

在新课初始阶段，教师所设置的问题直接影响着教学重点引入的效果.对此提高问题引入的有效性，帮助学生奠定一个良好的知识建构的开端应是教师培养学生逻辑推理素养的首要步骤.在具体的操作中，建议从以下两个方面展开.

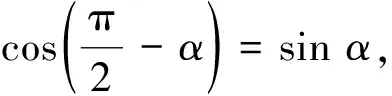
(2)结合本节课的教学重点引入探究问题.由于上述两个诱导公式所表示的均为特殊角与任意角α的和或差的三角函数与该任意角α的三角函数恒等关系，故本节课的教学可以将问题设置为：如果将特殊角换为任意角β，那么任意角α与β的和或差的三角函数与α,β的三角函数存在什么关系？通过引入该问题帮助学生作好推理准备.

2 问题解决，优化推理过程

本节课将问题解决作为主线，在教师的引导下使学生主动地参与到两角差的余弦公式推导活动中，师生共同探索结论产生的过程，对两角差的余弦公式追根溯源.

首先，教师在屏幕上呈现图1；其次，教师引导学生观察图1，回顾课堂初始环节所提出的问题；最后，师生共同推导两角差的余弦公式.公式推导环节如下：

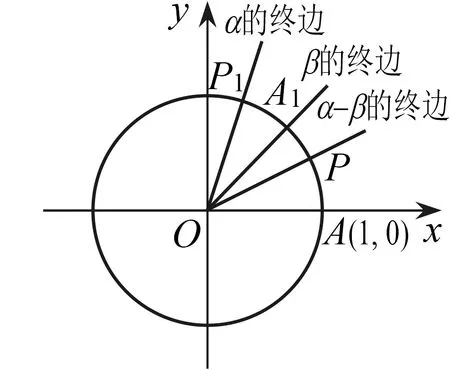
图1

环节1 师(思路疏导)：在问题解决的过程中，我们需要明确图中给出的已知条件，通过初步的观察我们可以明确，图中x轴与y轴垂直相交于圆心O，如果令α≠2kπ+β，k∈Z，且圆与x轴的正半轴交点为A(1, 0)，以x轴的正半轴为始边开始作角α,β,α-β，那么α终边、β终边、α-β终边与单位圆的交点分别为点P1(cosα, sinα),A1(cosβ,sinβ),P(cos(α-β),sin(α-β)).现在同学们将屏幕上的图、刚才老师所拟定的假设以及α终边、β终边、α-β终边与单位圆的交点分别写到草稿纸上.

环节2 师：在问题解决的过程中我们可以利用圆的什么特性？线段AP与A1P1之间存在什么关系？为什么？通过上述问题引导学生开展小组探究.

环节3 小组合作探究交流汇报，教师适时将学生汇报过程中有价值的信息板书在黑板上.若某个小组所作的汇报没有呈现公式推导的完整性，可以鼓励其他小组予以补充.

环节5 师(板书)：cos2(α-β)+sin2(α-β)=1，cos2α+sin2α=1，cos2β+sin2β=1.要求学生对(*)化简，组内对比化简结果是否一致，请学生在黑板上板演化简过程.

环节6 师(第二次公式推导总结)：回顾公式推导的条件，即α≠2kπ+β，k∈Z，将这一条件代入化简后的等式中，公式是否成立？给学生3～5分钟的时间，教师总结：无论角度如何变化，图1中各个点的坐标均不会发生改变，线段AP始终等于A1P1，对于任意角α与β，都有Cα-β=cos(α-β)=cosαcosβ+sinαsinβ，我们将其称为两角差的余弦公式.

3 随堂习题，训练推理能力

3.1 凸显数学思想

数学思想是学生逻辑推理能力的基础和源泉，所以在训练学生推理能力的过程中，教师应将习题作为载体，使学生通过问题解决获得对某一数学思想的深入理解.在上述公式推导环节结束后，教师将随堂习题作为载体凸显从一般到特殊的数学思想，强化学生问题解决的能力.随堂习题设计如下：

用Cα-β推导(过程略).

师(总结)：在问题解决的过程中我们需善于利用一般到特殊的数学思想.

3.2 活用数学公式

公式的灵活应用不仅关系解题效率，同时也彰显逻辑推理能力水平.本节课中，教师侧重于训练学生灵活应用数学公式，打破思维的局限性，呈现随堂习题“计算cos 105° cos 60°+sin 105° sin 60°”.

师(点拨)：是否可以从右到左逆向使用公式Cα-β？

教(总结)：懂得活用公式，除从左到右应用外我们还可以从右到左应用公式.

为强化公式逆用能力，可呈现习题“计算 cos 15° cos 105°+sin 15° sin 105°”，要求学生自主解答.此外，为提升学生活用数学公式的能力，教师在总结后可呈现习题“计算cos(-15°)”，要求学生采用两种方法解答.

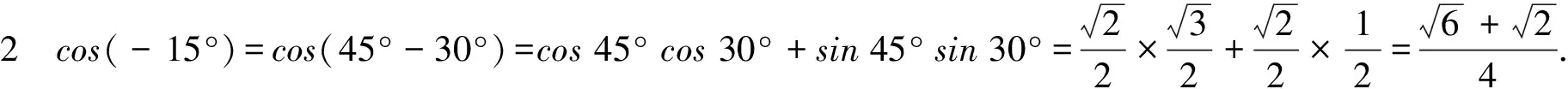
3.3 适当创造条件

部分习题不能直接运用公式求解，教师需要培养学生创造条件的意识.在本节课中教师可呈现随堂习题“计算cos 65° cos 20°+cos 25° cos 70°”.

师(点拨)：我们是否可以通过创造条件将公式变形，然后利用Cα-β求解？

求解过程略.

师(总结)：在解决三角函数求值问题时，变角是常用的解题技巧，变角可以帮助我们揭示问题的本质.在运用公式的过程中需注意角的范围、三角函数值的正负以及特殊角的关系.

4 一题多变，揭示推理规律

随堂练习题虽然能对学生的推理能力起到训练、提升的目的，但学生对于教师的总结仍存在较强的依赖，所以随堂练习题存在一定的局限性.教师还应关注推理过程中规律和方法的揭示，使学生能够挖掘各个习题背后隐藏的规律.一题多变是达成此目的的有效手段，本节课中教师可通过下述例题的解决，使学生理解已知三角函数值求角的问题需要结合三角函数值与角的范围.需要注意的是，一题多变环节，教师不宜过多地指导和总结，应以学生自主解答和总结为主，教师启发为辅.

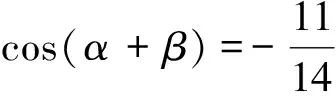
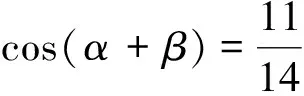
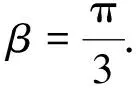
上述教学环节结束后，教师应提出“已知三角函数值求角问题的推理过程”等问题，提升学生问题解决的推理能力.

5 结束语

培养学生的逻辑推理能力，无论是推导公式、还是问题解决的推理技巧，教师均应关注教学环节中学生的参与度，一方面将学生作为课堂教学的主体使其积极参与推理的过程，另一方面在创设充足的推理训练机会的基础上剔除过多的教学干预，利用问题鼓励全班学生自主推理.另外，基于“问题解决”的推理教学，“问题”应贯穿于教学始终，教师需重视“问题”对于培养学生推理能力所承载的育人价值.

编者按为密切编辑部与中学的联系，本刊编委第27次“走进课堂”，于2021年10月25日赴江苏省太仓高级中学观课议课.江苏省太仓高级中学建校于1907年，“废科举，力行新学”，初名为太仓州属中学堂.办学115年来，虽十六易名，三迁校址，却不改太仓高中是江苏省内独树一帜、不可或缺的优质中学校本色，1997年学校被确认为江苏省重点高中，1999年率先成为国家级示范性普通高中，2004年3月被评为江苏省首批四星级高中.学校秉承“循正守真，志远业精”规划发展总体思路，谋求项目化、特色化创新发展之路，逐步形成“志远育德，业精育才”课程体系，建成彰显“人文奠基，科技见长”办学特色课程基地群，强化办学理念、师资队伍、课程实施、学校治理、育人模式和办学特色建设，形成了可资借鉴和可供推广的高品质高中经验.