一种基于矩估计的低轨卫星频谱感知方法

张福来，王中豪，余琪琦，覃团发*

(1.广西大学 计算机与电子信息学院，广西 南宁 530004；2.广西大学 广西多媒体通信与网络技术重点实验室，广西 南宁 530004)

0 引言

近年来，卫星通信正在迅速发展[1]。在现有的卫星类型中，低地球轨道(Low Earth Orbit,LEO)卫星因能提供更短的往返延迟而变得越来越重要[2]。LEO卫星一般运行在500～1 500 km的高度[3]，相对于地球静止轨道卫星(Geostationary Earth Orbit,GEO)卫星，发射成本较低，这使得LEO卫星网络更有可能实现全球覆盖。例如SpaceX,OneWeb和LeoSat等公司都宣布了超大星座卫星网络计划[4]。多卫星协同通信与星地协同通信正变得越来越重要[5-7]。

目前，卫星频谱的分配方式主要是固定分配。随着卫星数量的不断增加，频谱作为不可再生资源将严重制约空天地一体化网络(Space Air Ground Integrated Network,SAGIN)的未来发展[8]。特别是在LEO-GEO共存的卫星系统中，频谱资源的稀缺将迫使不同的卫星在同一频段工作，共享同一频段资源[9-10]。因此，如何在运行于不同轨道平面上的卫星星座之间更合理地分配和共享频谱资源，将是未来卫星系统设计中亟待解决的问题之一。

认知无线电(Cognitive Radio,CR)在解决无线通信频谱稀缺问题上是一种很有前途的技术[11]，它允许次级用户(Secondary User,SU)在不影响主用户(Primary User,PU)使用的情况下机会性地访问空闲的频谱资源[12]。近年来，研究人员注意到CR技术也可以很好地应用于卫星通信系统[13-14]。频谱感知(Spectrum Sensing,SS)是CR的关键环节，其目的是识别空闲频率信道，进而合理地分配空闲频谱资源，从而解决频谱稀缺问题。在卫星系统中，频率共享场景可以由GEO卫星和LEO卫星共存来表示。根据Radio Regulations的政策[15]，次级卫星系统必须避免对现有的主卫星系统造成有害干扰。因此，需要有效的SS方法来判断LEO信号的存在与否。

在卫星通信中，利用CR技术整合频谱资源已成为提高频谱利用率的有效途径[16]。对于认知卫星通信，文献[17]提出了一种频谱决策框架，采用广义似然比检验和最大后验准则推导出合理的决策阈值，对检测性能进行综合分析，验证了提出方案的可行性。文献[18]为解决LEO卫星与GEO卫星的共线干扰问题，提出了一种LEO协同SS方案。通过功率分配优化和LEO卫星的协同配合，以确保LEO卫星的服务不会降低GEO卫星的服务质量(Quality of Service,QoS)，使GEO卫星系统可以更好地应对LEO卫星的干扰。文献[19]利用假设检验和最大后验来检测影响GEO系统的非地球静止轨道(Non-geostationary Earth Orbit,NGEO)卫星信号。此外，研究者还将该方法的性能与传统的SS方法进行了比较，传统的检测方法是由能量检测器(Energy Detector,ED)表示。卫星系统具有低信噪比(Signal-to-Noise Ratio,SNR)和噪声不确定等特性，较低SNR是由于星地距离过长，导致链路损失大；噪声不确定则是不同层的卫星间存在干扰所引起的。在卫星系统中，单独使用ED算法会产生明显的检测性能退化问题[20]。近年来，研究者提出了一种基于矩估计(Moment Estimation,ME)的SS方法[21]，可克服ED在噪声不确定下性能衰退的缺点。

本文提出基于ME算法的认知卫星通信SS方法来快速可靠地检测LEO信号。利用接收信号的周期平稳性、二阶矩和四阶矩来正确估计接收信号中LEO卫星信号功率。具体来说，根据接收信号样本的二阶矩和四阶矩的线性组合估算出LEO信号功率，将其作为决策变量，用来判断是否存在空频率信道。计算结果表明，在低SNR和噪声不确定的情况下，本文提出的方法与传统ED算法和文献[19]中提到的算法相比有更好的性能，且计算复杂度的增加可以忽略不计。

1 系统模型

本文研究了星地之间的SS策略，下行链路卫星系统模型如图1所示。

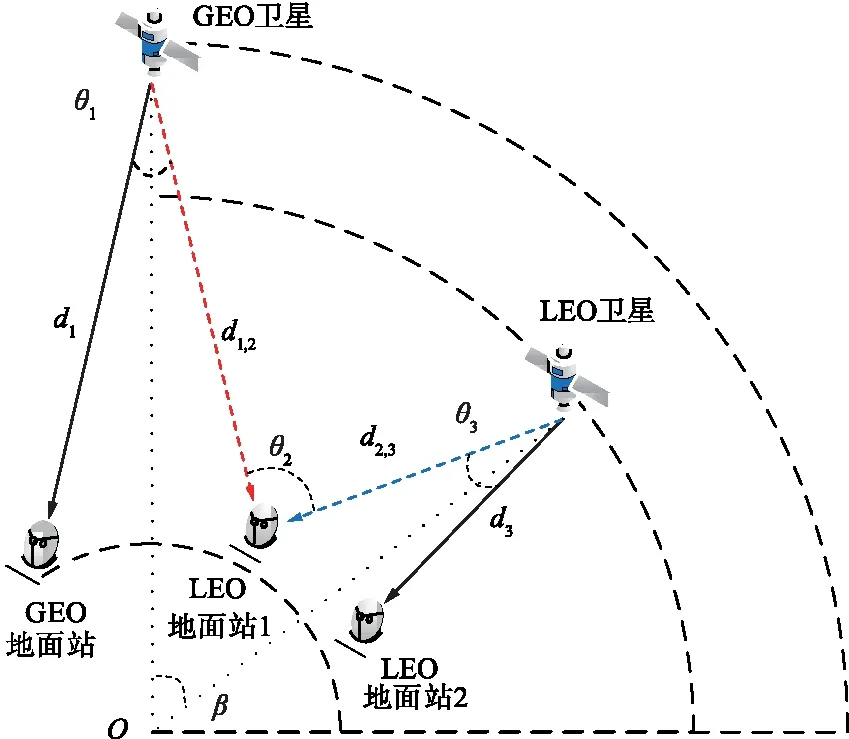
图1 下行链路卫星系统模型Fig.1 Downlink model of satellite system

对双卫星系统中LEO卫星受到GEO卫星不确定干扰时的SS问题进行数学建模。因为在LEO卫星下行链路和上行链路阶段感知环境只是参数值的不同，所以本文只研究下行链路阶段。本系统模型共有3层结构：GEO卫星层、LEO卫星层和地面用户层。GEO卫星层作为SU机会性地对LEO卫星频谱进行感知和接入。LEO卫星层作为PU，可为GEO卫星提供机会性的空闲频谱。在地面层，地面站根据接收信号种类不同通常分为3种情况：GEO地面站只能接收GEO信号，LEO地面站1可同时接收GEO和LEO卫星信号，LEO地面站2只能接收LEO信号。本文重点研究LEO地面站1的SS模型。由图1可知，GEO卫星到地面的距离为Hge，LEO卫星到地面距离为Hle，地球半径为r。因为GEO卫星相对于地面静止不动，所以GEO卫星到地面站的距离可以预先知道，即d1,2已知。在LEO绕轨做周期运动时，β的变化也具有周期性，因此，θ3和d2,3可由β，Hge+r，Hle+r和d1,2推导。因为β是唯一变量，所以可以得到θ2，θ3和d2,3与β相关。

2 单一LEO卫星信号数学建模

假设LEO卫星的功率从M个不同等级中产生，即PlsM>…>Pls1>0。另外，假设在卫星的发射周期内LEO的功率固定不变[19]。为了便于分析，还假设地面站指向LEO卫星，且地面站位于其主波束中(对于地面站未直接指向LEO卫星的情况，接收功率添加波束损失因子即可)。因此，在功率等级为Plsm,m=1,2,…,M时，判断LEO卫星是否存在的二元假设，可表示为：

(1)

式中，xlsk表示在第k个LEO地面站接收到的信号；噪声nk表示加性高斯白噪声，有nk～CN(0,σ2)；φ表示信道传输相位，假设信道相位服从均匀分布，即φ～U(0,2π)，因为能量检测本质是检测能量值大小，因此φ不会影响检测结果；slsk表示第k个LEO卫星的发射信号，有slsk～CN(0,1)；hls表示比例因子。由式(2)计算得到：

(2)

式中，Gle(θ2)表示LEO地面站的接收天线在θ2方向上的最大增益；Gls(θ3)表示LEO卫星在θ3方向上的最大增益；c=3×108m/s；f表示卫星的频率；d2,3表示LEO卫星到地面站的距离；Ag表示气体吸收因子；Ac表示云或雾的吸收因子。Ag和Ac计算如下：

Ag=Aw+Ao，

(3)

Ac=KlM，

(4)

式中，Aw是由干燥空气引起的特定衰减；Ao是由水蒸气引起的特定衰减；Kl是云层特定衰减系数；M是云或雾的液态水密度。

由系统模型可知，θ2，θ3和d2,3与β相关，式(2)最终可以写成：

(5)

基于上述前提，可以认为xlsk也是一个复对称高斯随机变量，即：

(6)

与文献[19]不同，本文中合理假设LEO地面站只检测LEO卫星信号和噪声信号，然后LEO地面站可将感知信息结果传输给GEO卫星。但LEO地面站也可以接收GEO卫星信号，如果检测LEO卫星没有接入LEO地面站，则GEO卫星可以机会性地以全部功率接入LEO地面站；相反，如果LEO卫星处于服务状态，GEO卫星则禁止接入。

3 矩阵化LEO卫星信号的数学建模

受文献[20]的启发，本文提出基于ME的LEO卫星SS方案。利用接收信号的二阶矩和四阶矩来正确估计发射LEO信号的功率，并将这种方法应用到LEO卫星通信之中。一旦LEO信号功率能够被有效估计，这个估计量便可作为决策统计量来表明被测数据中是否存在LEO信号。若LEO信号存在，则表示该频段正在被使用；若LEO信号不存在，则表示该频段正处于空闲状态，GEO卫星可选择性接入使用。

为了判断被测频段中是否存在LEO卫星信号，式(1)可以重新表述为：

(7)

式中，n代表K维列向量的噪声，服从实高斯分布，即n～N(0,σ2I)；s代表K个接收信号样本的K维列向量，即：

(8)

利用接收信号的二阶矩和四阶矩来精确估计LEO卫星的功率。首先，计算了LEO地面站的接收信号二阶矩和四阶矩；然后，推导出LEO信号的功率；最后，得到作为判断LEO卫星是否存在的决策指标。设δ为接收信号的二阶矩，则：

δ=E[|s+n|2]=E[(s+n)H(s+n)]=

E[sHs+sHn+nHs+nHn]=

E[sHs]+E[sHn]+E[nHs]+E[nHn]，

(9)

式中，E(·)表示统计期望；|·|表示模值；(·)H表示共轭转置。假设LEO信号与噪声都是独立同分布(Independently Identical Distribution,IID)变量，即LEO信号与噪声之间不相关，可以得到：

E[sHn]=E[nHs]=0。

(10)

式(9)可以重新写为：

δ=E[sHs]+E[nHn]=

(11)

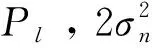
(12)

式中，rk为接收信号的第k个信号样本。

同理，四阶矩ϑ可以表示为：

ϑ=E[|s+n|4]=E[((s+n)H(s+n))2]=E[(sHs+sHn+nHs+nHn)2]=E(sHs)2+(nHn)2+4sHsnHn+(sHn)2+(nHs)2+2sHssHn+2sHsnHs+2nHnsHn+2nHnnHs。

(13)

假设噪声和信号的实分量和虚分量是正交的，因为LEO信号s和噪声n不相关，可以得到：

(14)

因此，式(13)可以重新写为：

ϑ=E[(sHs)2+(nHn)2+4sHsnHn]=E[(sHs)2]+E[(nHn)2]+

(15)

式中，μs为信号的峰度；μn为噪声的峰度。假设信号和噪声都具有恒定的包络，即在每个复高斯分布过程下信号峰度μs恒为1，噪声峰度μn恒为2。因此式(15)可以写为：

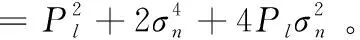
(16)

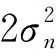
(17)

(18)

为了避免处理复数，假设决策统计量是LEO信号功率的平方估计，即决策统计量Φ为：

(19)

当K值很大时，检测统计量Φ是渐近高斯变量，因为第1项是均值为0的渐近高斯变量的平方。第2项是随机变量和函数，根据辛钦大数定律(Wiener-Khinchin Law of Large Numbers)可知，第2项同样是渐近高斯变量。因此可以得出，理论上对于较大的K值，检测概率Pd的性能可以近似地被计算出来。检测阈值λ是在H0的假设下通过虚警概率Pf而直接得到的[22]：

(20)

式中，erfc-1(·)表示互补误差函数的逆。一旦计算出检测阈值λ，根据假设H1就可推导出检测概率Pd：

(21)

4 仿真结果与分析

4.1 仿真参数设置

对提出的基于ME的SS算法进行性能分析，以检测概率Pd作为衡量指标，通过104次独立试验的蒙特卡罗模拟估算出来。参考文献[19]的仿真下行场景，仿真设置的参数值如表1所示。

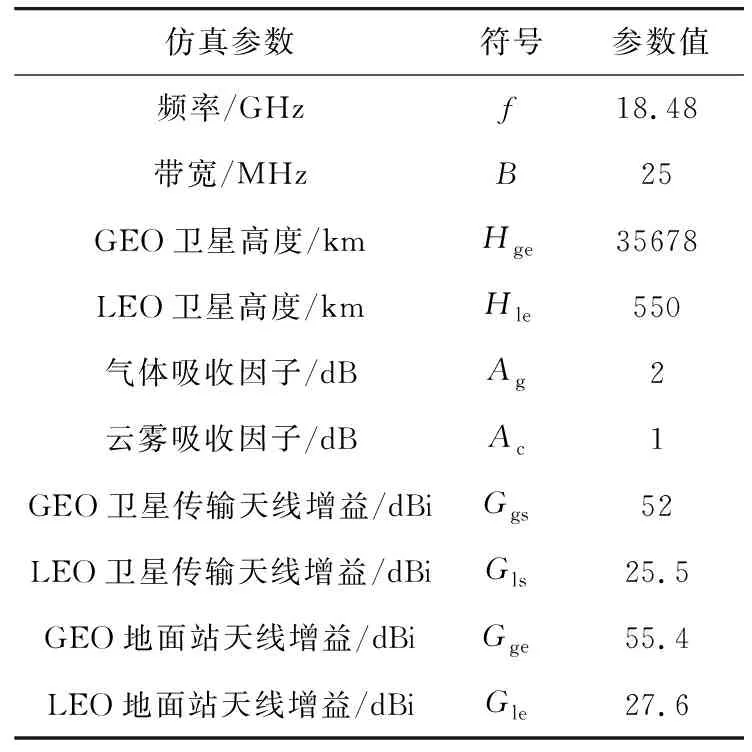
表1 仿真参数Tab.1 Simulation parameters

假设虚警概率Pf=10-2，LEO卫星的发射功率分别设置为Pls1=6 dBw，Pls2=12 dBw和Pls3=20 dBw，各个发射功率所对应的先验概率分别为Pr(Pls1)=0.3，Pr(Pls2)=0.2和Pr(Pls3)=0.1，并且LEO卫星不发射功率的先验概率Pr(Pls0)=0.4。

4.2 感知方法比较

公开文献中，选择2种经典的卫星检测算法与本文方法进行比较：方法1是ED[23]；方法2是频谱感知与识别法(Spectrum Sensing and Recognition,SSR)[19]。ED是最简单和广泛使用的SS方法，其决策统计量是从采集的接收信号样本中依次获得的能量总和。SSR采用高斯混合模型所获得的决策统计量υ为：

(22)

式中，A，B，Z，T的表达式分别为：

(23)

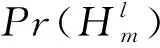
前文提到，只有在LEO卫星不发射信号时，GEO卫星信号才会发射信号接入LEO地面站。因此，在仿真分析中只关注不同噪声环境对3种方法所产生的影响。

4.3 仿真结果分析

首先，分析接收机的样本数量对3种方法所产生的影响。仿真参数设置为Pls=20 dBw和Pf=10-2，K值分别为102和103。仿真结果如图2所示。

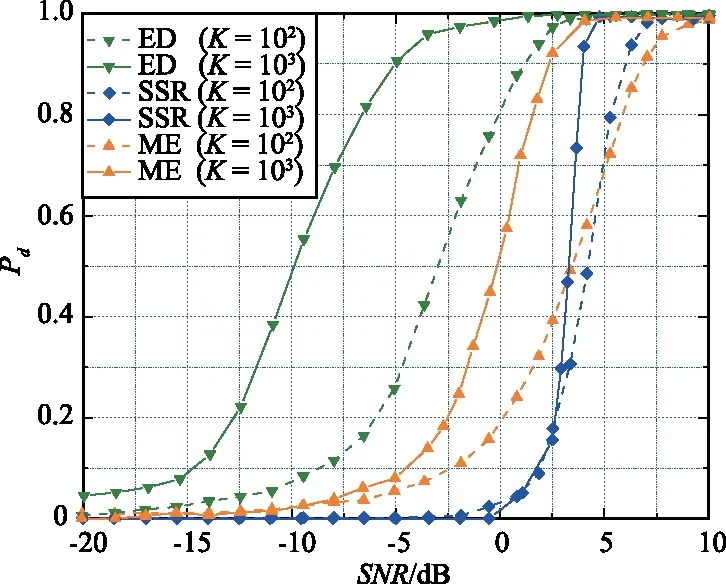
图2 不同接收样本K下3种方法的性能比较Fig.2 Performance comparison of three methods under different receiving sample K

由图2可以看出，在固定发射功率下，样本数量K值、检测概率Pd值和SNR的关系。图中的数据通过标准蒙特卡罗模拟数值计算得到。随着样本数量K的增加，ED算法和ME算法都能够达到越来越好的检测概率Pd值，但是SSR算法几乎保持相同的检测能力。

理想ED算法指的是假设ED算法可以获取噪声方差的全部信息，但是在现实中很难实现，这种获取部分噪声信息的情况会产生严重的性能损失。因此，在后续分析中，理想ED算法将作为性能基准，可以获取全部噪声功率信息，而ED算法则是只能获取部分噪声功率信息。

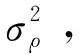
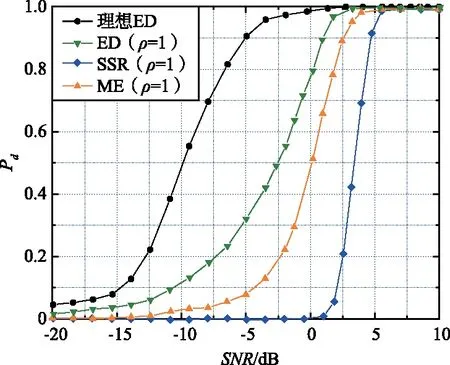
图3 当ρ=1 dB时3种方法的性能比较Fig.3 Performance comparison of the three methods when ρ=1 dB

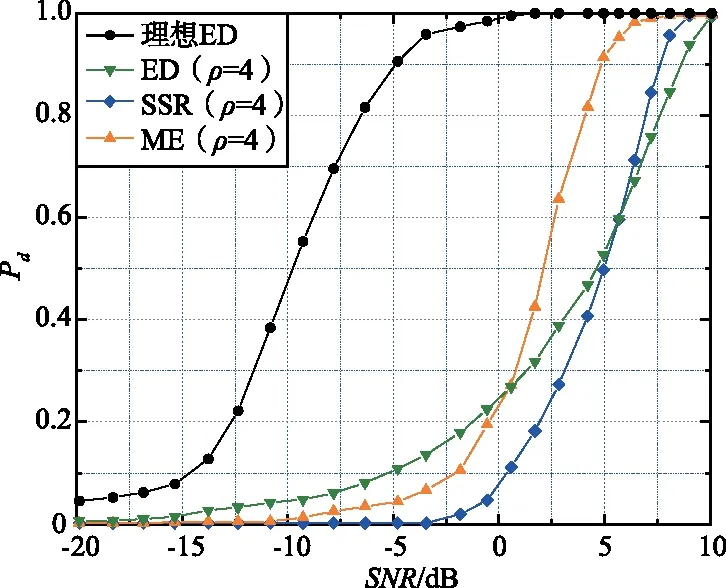
图4 当ρ=4 dB时3种方法的性能比较Fig.4 Performance comparison of the three methods when ρ=4 dB

图5 当ρ=8 dB时3种方法的性能比较Fig.5 Performance comparison of the three methods when ρ=8 dB

随着噪声波动的增加，ED方法出现了明显的性能退化，这说明ED算法的鲁棒性较差、抗干扰能力弱。对比SSR算法，虽然SSR算法比ED算法的鲁棒性高，但也出现了部分性能退化，且SSR算法整体的检验性能均低于ME算法。因此，可以说ME算法具有较强的鲁棒性，且相比于ED算法和SSR算法，在ρ=4 dB和ρ=8 dB下，ME算法能够确保LEO卫星系统的最佳感知性能。

最后，对LEO卫星频谱传感探测器进行能够体现检测LEO信号能力的研究，即检测LEO信号所需的平均检测时间(Mean Detection Time,MDT)。MDT是指正确检测所有样本平均需要的时间(即样本数量)，可以表示为[20]：

(24)

式中，Tp为惩罚时间，即系统从错误决策中恢复所需的时间。假设样本数量K、虚警概率Pf和惩罚时间Tp值相同，ρ分别取4，8 dB，假设MDTgain1表示SSR算法与ME算法的MDT之比，MDTgain2表示ED算法与ME算法的MDT之比，MDTgain1和MDTgain2可表示为：

(25)

因为过小的检测概率没有分析的实际意义，所以需要选择检测概率上升阶段的SNR区间。由图4和图5可知，信号的检测概率从5 dB左右到10 dB，检测概率性能迅速升高，SNR对检测概率影响明显，所以SNR选择[5, 10]dB进行分析，MDT增益比如图6所示。

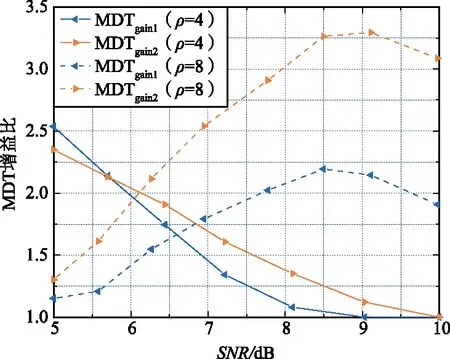
图6 MDT增益比Fig.6 Ratio of MDT gain

对比橙色的曲线可知，当ρ值增加时，噪声不确定性的区间同样也在增加，且噪声不确定性越高，ME算法的性能优势越明显，ME方案具有较强的鲁棒性。综上可以得出结论，比起现有的同类方法，本文提出的方法具有较强鲁棒性，且能够更快地对LEO卫星完成检测。

5 结束语

本文设计了一种基于ME的认知卫星通信SS技术。利用带有噪声的接收信号的二阶和四阶矩的线性组合估算出LEO信号的有效功率，将矩估计结果作为检测器的决策统计量。理论分析和仿真验证了该算法在卫星通信中的性能。结果表明，与传统ED算法相比，在相同条件下ME方法可以达到更高的检测概率和更短的检测时间，这些性能提升对认知卫星通信来说都是非常关键的。未来，在认知卫星通信方面的研究可以引入更复杂的系统模型，进一步提高检测性能和检测时间。