基于XFEM的预应力混凝土梁裂纹扩展研究

胡 筱 ， 庞 明 亮， 王 雨

(中国电建集团成都勘测设计研究院有限公司，四川 成都 610072)

0 引 言

自20世纪以来，混凝土在土木工程领域得到大量应用，已经成为当前使用量最大的工程材料。工程中，混凝土具有较明显的脆性特征，同时也具有强烈的非均匀性，其内部有宏观的缺陷，如裂纹、夹渣、气泡及孔穴等，在外荷载或者温度荷载作用下，易发生开裂破坏[1]。由于混凝土材料的特性，在各种应力条件下，受拉状态是混凝土相对最不利受力状态。工程中常见的混凝土开裂问题大多是由于拉应力超过混凝土材料抗拉性能引起的，典型现象如隧道衬砌变形开裂、早期大体积混凝土在温度应力作用下的膨胀开裂等，而这些现象的细观本质则是材料内部在荷载作用下裂隙、骨料胶结界面、孔洞等缺陷发生裂纹，继而扩展、贯通的断裂力学过程[2]。因此，研究混凝土断裂过程有利于认识混凝土开裂破坏的内在因素，进而为优化混凝土材料性能及预测混凝土开裂问题提供力学依据。

随着力学、数学理论的发展和计算机性能的提升，数值模拟逐渐成为研究材料断裂问题的一个有效手段，常见模拟材料断裂行为的数值模拟方法包括离散元法、有限元法、边界元法、数值流形元法等，其中应用最广的方法当属离散元法和有限元法。离散元法将材料离散为大量颗粒，颗粒间通过法向和切向不同的接触行为模拟真实材料的胶结状态，粒间件处理通过力-位移法则计算，而颗粒运动则通过牛顿运动定律描述；当荷载引起的应力超过接触强度准则时，粒间接触失效，宏观上即可模拟裂纹的萌生和扩展行为[3]。

离散元法抓住了材料细观离散的本质，在固体材料断裂力学行为的模拟及细观机理研究方面具有独特优势，但颗粒化的模型结构给离散元法模拟尺度带来了巨大局限。工程中，坝体、衬砌、梁柱等结构均属于较大～超大尺寸结构，在这样大尺度条件下模拟材料颗粒集合的力学行为，在当前计算机技术水平条件下，费时费财，难度颇大。有限元法将宏观材料视为连续均匀介质，通过网格划分将研究对象离散为计算单元，通过定义单元材料的应力应变本构关系，描述材料力学性质，并通过节点位移的连续协调实现模型的整体计算。传统有限元的计算理论决定了模型计算结果是连续的，对断裂问题的模拟一般通过网格重划分来实现，这种方式不仅工作量大，还存在新旧网格状态变量映射的问题[4]。20世纪90年代末，Belytschko教授团队[5-7]基于单位分解的思想首先提出了扩展有限元法(XFEM)，该方法通过引入不连续位移模式，使不连续位移场的描述独立于有限元网格划分，克服了传统有限元模拟断裂问题需要反复重新划分网格的局限性。20余年来，国内外学者开展了大量研究工作，使扩展有限元理论和应用水平得到了很大发展[8-11]。

1 ANSYS扩展有限元的基本原理

扩展有限元技术由于其不依赖网格划分、不需要预知裂纹扩展路径，在模拟固体材料断裂行为的研究中具有良好的应用前景。

1.1 单位分解思想

常规有限元方法用多项式作为形函数，精度依赖于多项式局部逼近特性，对于很多问题，这种单纯的多项式逼近效果并不够理想。1996年，Melenk 和Babuska[12]以及Duarte 和Oden[13]先后提出单位分解法。该方法的基本思想是将任意函数用其域内一组局部函数Ni(x)φ(x)表示，即：

(1)

式中Ni(x)为有限元形函数，其形式不限于普通多项式，且有：

(2)

1.2 扩展有限元法的基本方程

扩展有限元法基于单位分解思想，在计算时引入虚拟的节点附加自由度，将裂纹扩展引发的不连续位移进行分解，即分解为有限元模型节点的位移分量和裂纹扩展引起的界面不连续位移分量，可表示为下列显式函数[14]：

(3)

当考虑裂纹尖端应力集中引起的奇异性，则任意一点的位移向量还应增加一项反映裂纹尖端奇异性的位移分量，则总位移向量表示为：

(4)

(5)

1.3 水平集方法

由于扩展有限单元法允许裂纹穿过单元，即网格与间断面相互独立，因此，需要对间断面进行几何描述，常用方法为水平集方法(level sets method)[15]。另一方面，在XFEM中构造扩充形函数时往往也需要借助水平集函数。水平集方法是一种分析、计算并追踪界面运动的数值方法，用与空间、时间有关的水平集函数f(x(t),t)来描述与网格无关的间断。因为增加了时间变量，所以水平集函数要比间断的维数高出一维。在计算过程中，间断上的点始终满足f(x(t),t)=0的条件。

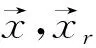
(6)

2 基于ANSYS XFEM的混凝土梁裂纹扩展模型

本文基于ANSYS XFEM，在二维条件下对比模拟预制裂纹的简支混凝土梁在集中荷载作用下，有无预应力情况下的裂纹扩展行为。带预制裂纹的简支混凝土梁受跨中集中荷载示意见图1。

图1 带预制裂纹的简支混凝土梁受跨中集中荷载示意图

为此，建立ANSYS有限元模型，简支混凝土梁及裂纹有限元模型见图2，模型共计3 131个节点，3 000个单元，单元类型采用PLANE182二维单元；模型底面左右侧节点处施加y方向法向位移约束，跨中顶部沿-y方向从0开始逐渐施加3 000 kN的集中荷载，并约束跨中顶部x方向位移。

(a) 无预应力混凝土梁

(b)预应力混凝土梁图2 简支混凝土梁及裂纹有限元模型

混凝土及预应力筋力学参数见表1；混凝土裂纹扩展准则采用最大周向应力准则，启裂最大周向应力值设定为1.78 MPa；预应力筋的模拟采用温降法实现，张拉力为1 333 kN，为消除钢筋弹性模量、泊松比对于裂纹扩展的影响，故取钢筋弹性模量、泊松比与混凝土相同，仅保留预应力效果。在跨中荷载作用下，裂纹扩展计算过程最大子步数100步，每子步0.01 s，总时长1 s。

表1 混凝土及预应力筋力学参数表

3 裂纹扩展结果分析

通过建立扩展有限元模型并进行计算，并对混凝土梁应力变形、裂纹扩展特征进行监测。

混凝土是一种抗压不抗拉材料，混凝土简支梁的底部裂纹扩展是否剧烈与梁的跨中竖向位移有着密切的联系。图3为有、无预应力条件下，混凝土梁顶部荷载-顶部位移图，图4为有、无预应力条件下，混凝土梁顶部荷载—最大裂纹宽度图。

图3 混凝土梁顶部荷载-顶部位移图

图4 混凝土梁顶部荷载-最大裂纹宽度图

在表示混凝土梁顶部荷载-顶部位移的图3中，由于预应力的作用，混凝土梁产生反弯现象，预应力梁跨中顶部竖向位移初值略大于0；在F=1 400 kN之前，有、无预应力梁的跨中顶部竖向位移均呈现直线下降趋势，且两直线段的斜率基本一致，这说明在这段区域，混凝土梁产生稳定的形变且未发生裂纹扩展，这一结论也由混凝土梁顶部荷载-最大裂纹宽度的图4中F=1 400 kN前裂纹张开宽度基本为0所验证。在图3中，无预应力梁的跨中顶部竖向位移于F=1 400 kN发生突变，有预应力梁的跨中顶部竖向位移于F=2 250 kN发生突变，结合图4的裂纹宽度突变点分析，跨中顶部竖向位移突变为底部裂纹发生扩展所导致，这说明混凝土裂纹的扩展均需达到某个临界点才会发生。图3、图4中均可见预应力梁的稳定段更长，突变段更短，突变之后还有稳定段；而无预应力梁一旦进入突变段，突变速度将越来越大；可见，预应力可以有效地增加裂纹起裂的临界荷载，且有效控制裂纹起裂后的扩展速度。

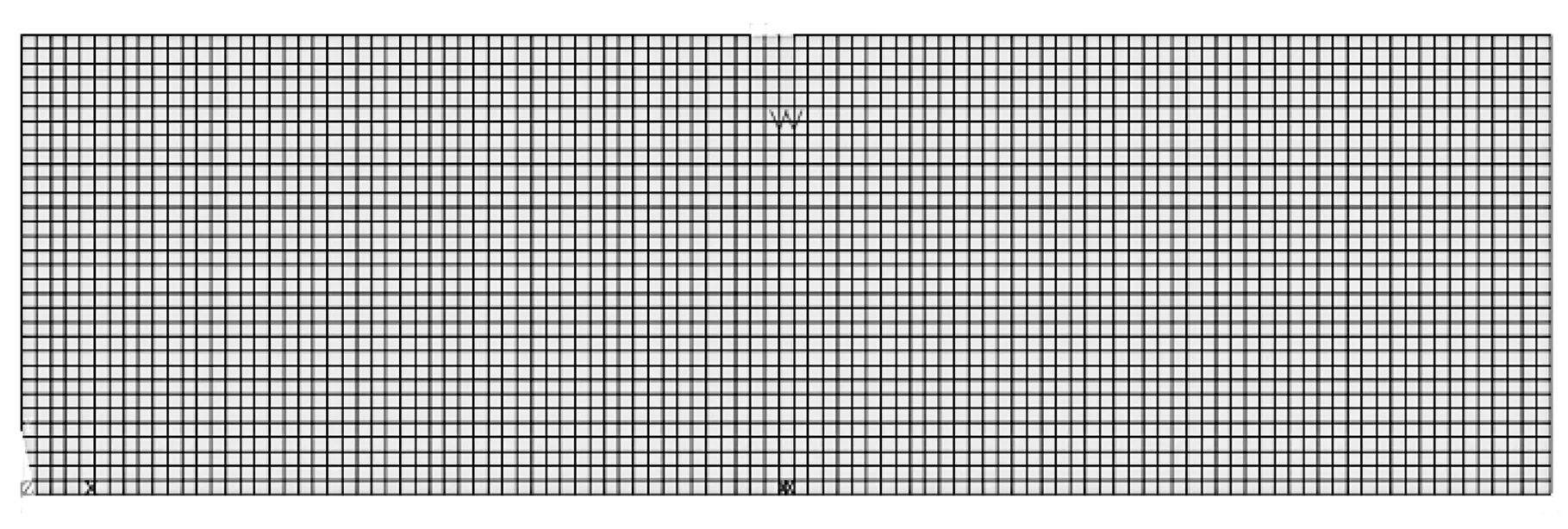
图5为无预应力条件下，混凝土梁的裂纹扩展过程von mises应力云图，从图5(b)可见，当F=1 500 kN时，无预应力混凝土梁只有轻微的起裂现象，而在裂纹起裂以后，随着荷载的增加和混凝土完整性的降低，裂纹开始迅速扩展，当F=3 000 kN时，裂纹长度已达2.095 m。

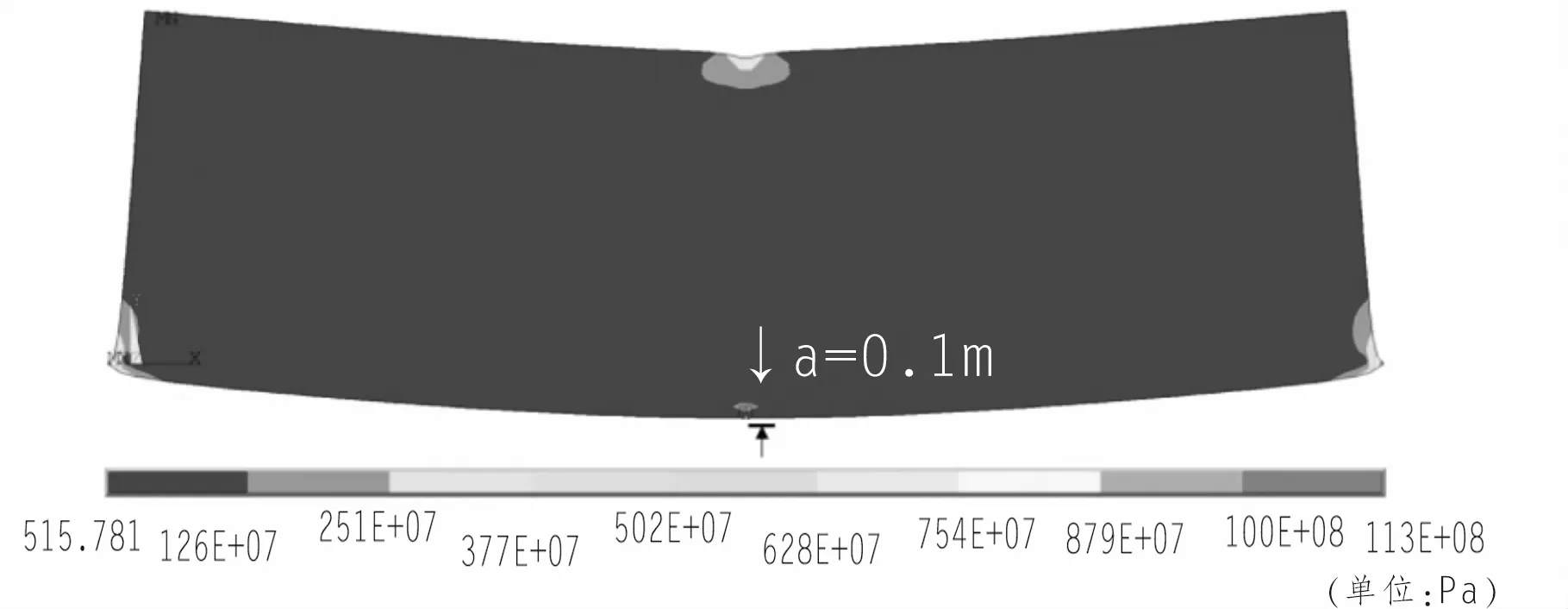
(a)F=750 kN

(b)F=1 500 kN

(c)F=2 250 kN

(d)F=3 000 kN图5 无预应力混凝土裂纹扩展过程von mises应力云图

图6为预应力条件下，混凝土梁的裂纹扩展过程von mises应力云图，从图6(a)可见，当F=2 250 kN时，预应力混凝土梁还未起裂；从图6(b)可见，当F=2 310 kN时，相比F=2 250 kN仅增加60 kN，但裂纹长度已达到0.286 m，相比无预应力条件下图5(a)扩展到图5(b)所增加的750 kN，有预应力条件下的裂纹扩展更加突然和剧烈；由图6(c)、6(d)，在裂纹长度扩展至0.381 m后，集中荷载F由2 370 kN增加630～3 000 kN，裂纹长度并未继续扩展，也说明了在预应力的作用下，裂纹扩展比无预应力条件下更加突然；

(a)F=2 250 kN

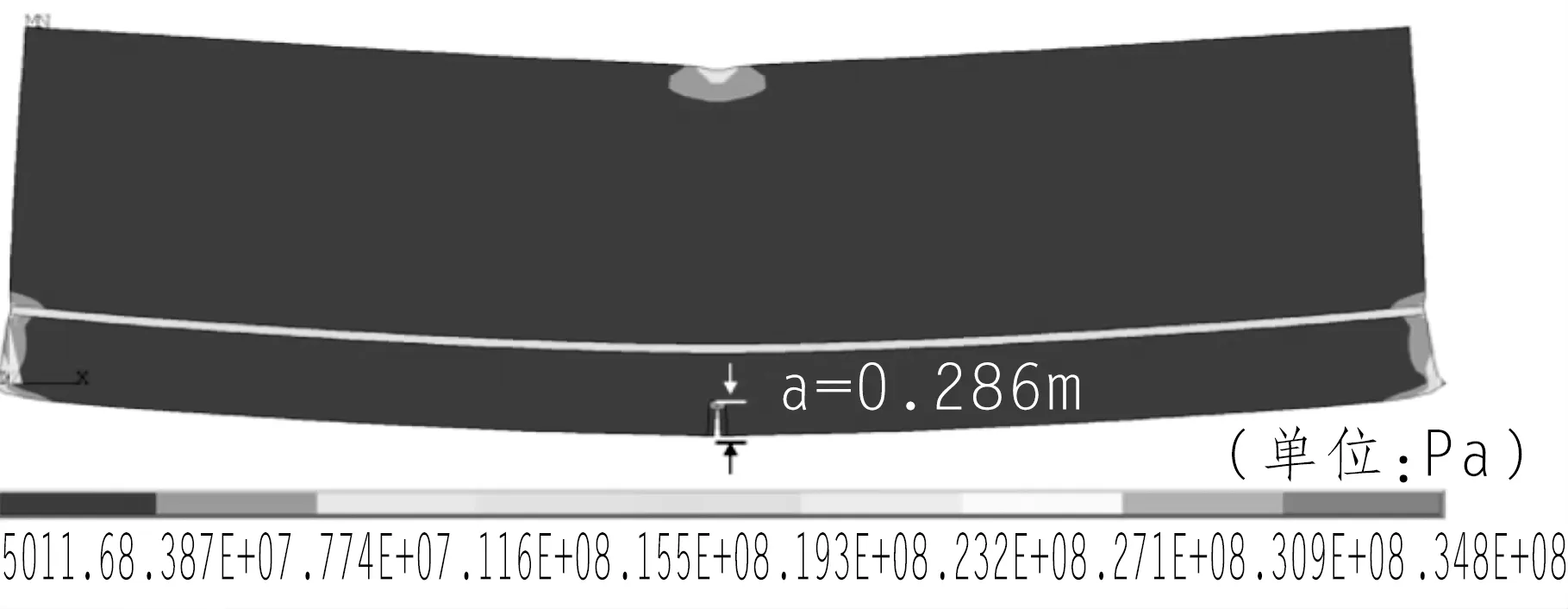
(b)F=2 310 kN

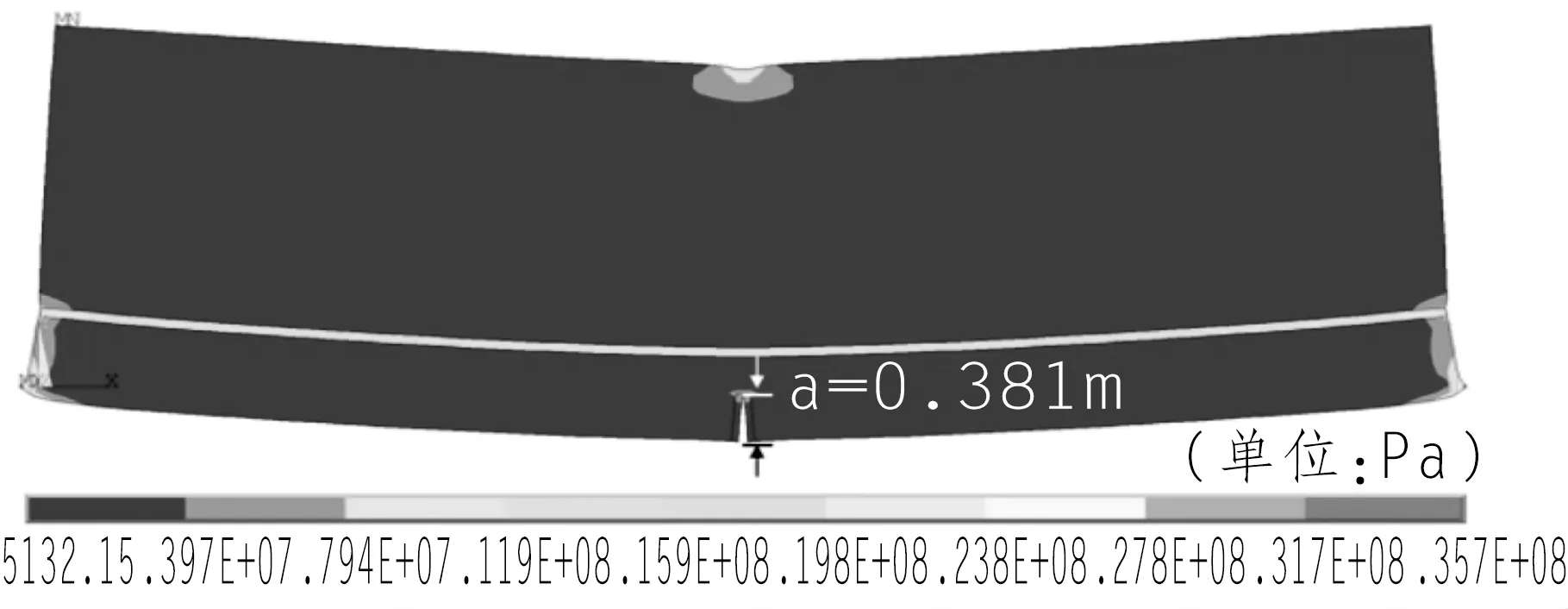
(c)F=2 370 kN

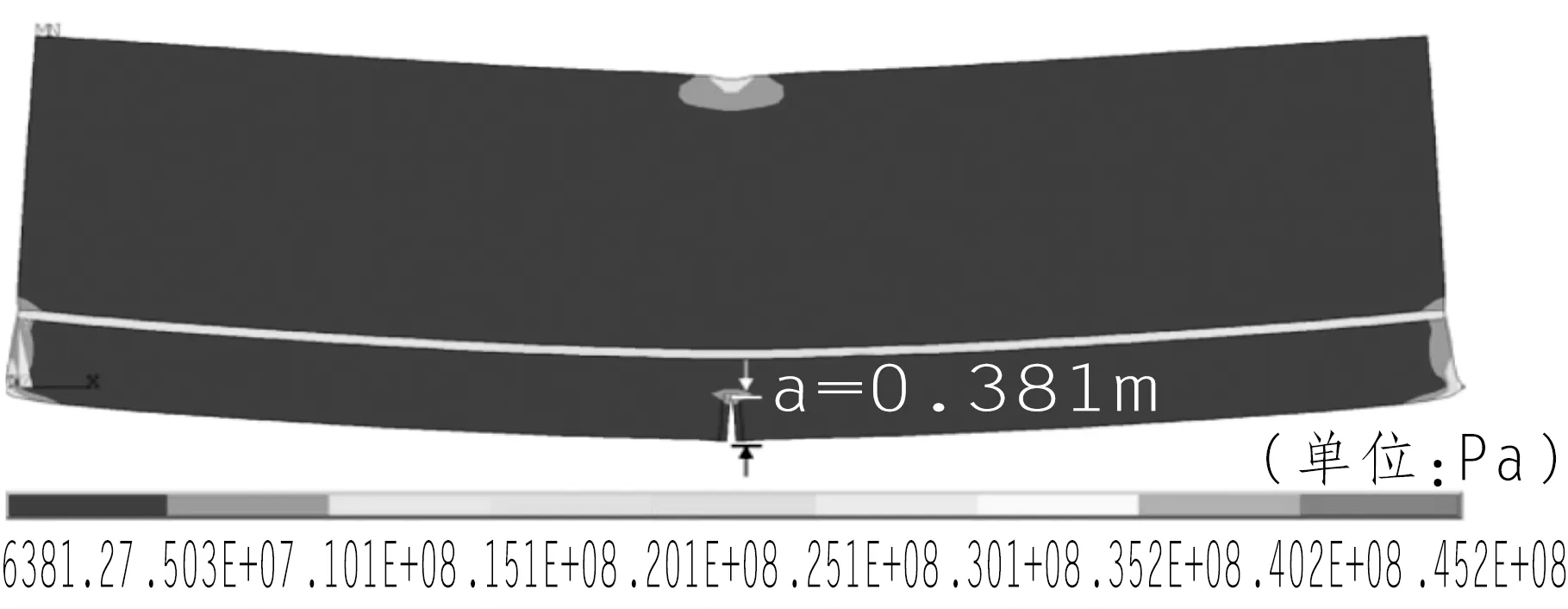
(d)F=3 000 kN图6 有预应力混凝土裂纹扩展过程von mises应力云图

而在裂纹突然扩展后，预应力混凝土梁不会发生如无预应力混凝土中的裂纹连续扩展，而是随着荷载的增加发生逐段的突变扩展。综合图5和图6，可以看出预应力可以明显提升混凝土的抗裂性能，可以有效控制裂纹的扩展长度及张开宽度。

4 结 论

混凝土开裂多是由于混凝土材料中拉应力超过抗拉极限引起的，在工程中常用预应力来增强混凝土整体的抗拉性能。通过对有、无预应力的预制裂纹混凝土梁在ANSYS中进行逐级加载的扩展有限元分析，比较其变形特征及裂纹扩展特征，可得到以下结论：

(1)混凝土裂纹的扩展需达到临界荷载才会发生，预应力的施加可以有效提高混凝土开裂的临界荷载；

(2)混凝土的裂纹开裂是突然的，而预应力的施加会加剧这种开裂的突然性，预应力混凝土的裂纹开裂会更加剧烈；

(3)无预应力混凝土梁的预制裂纹一旦开裂，裂纹将随着荷载的增加而连续扩展，且扩展速度越来越快，而预应力的施加会改变裂纹扩展模式，使得裂纹随着荷载的增加发生逐段的突变扩展；

(4)在相同荷载作用下，相比无预应力混凝土，预应力的施加显著降低了底部裂纹的扩展长度及裂纹最大张开宽度，有效的控制了裂纹扩展。