天津市综合性公园湖泊景观形态设计定量研究
付一丁,吴 军,李鹏波
(天津城建大学 建筑学院,天津 300384)
“园以水活”,湖泊景观具有丰富的景观空间和形式,不仅增添生机与色彩,还能传递平静怡神的氛围信息,所以湖泊景观对城市综合公园整体设计十分重要.设计时常以湖泊景观为中心布置园路、景点等其他要素,从而起到引导游人、拉长游览路线、分隔视线、调节小气候等作用.城市综合公园湖泊形态或曲或直,或狭长或开阔,不同形态表达着不同的美,也影响着公园空间布局的变化.因此,深入研究湖泊形态是城市综合性公园景观设计发展的必然要求.
建国以来,天津积累了大量的城市综合性公园,深受市民喜爱,满足研究可行的基础环境要求.另外,天津海河支流遍布,水景形式多样,天津人民对水有着与生俱来的亲切感.天津市各综合公园在条件允许的情况下,基本都建有湖泊景观,为天津综合性公园湖泊景观形态设计定量研究提供了数据来源.
1 调研公园选择
以2011年天津市市容园林委公布的《天津市公园名录》(近年未更新)为主要范围进行选择有湖泊景观的综合性公园(见表1).以《城市绿地规划标准》(GB/T 51346—2019)[1]中对综合公园的要求为根据,补充近年来新建的城市综合性公园,以保证数据的完整性和更新性.具体要求为:一是综合公园适宜规模不小于10公顷;二是要具备包括运动健身、儿童游戏、休闲游览、公共服务等多种功能在内的设计分区;三是要便于周围居民使用.另外,城市综合性公园湖泊景观应具有一定规模且运行良好、湖岸优美,因此选择湖泊面积≥1公顷且湖泊形态不完全规则的公园,避免出现水体形态量化的极端数值.

表1 天津市综合性公园名录
根据上述要求,筛选出24个天津城市综合性公园,包括水上公园、南翠屏公园、长虹生态园、绿水园、北宁公园、桥园公园、二宫公园、人民公园、西沽公园、双青公园、东丽湖自然艺苑、月牙河公园、水西公园、梅江公园、河滨公园、绿岛公园、新港公园、河西公园、大港公园、泰丰公园、渤龙湖公园、印象海堤公园、华翠公园、方舟公园,并对其湖泊景观进行调查与研究.
2 研究对象与数据转化分析
2.1 研究对象
在实地调研过程中,对照0.46米/像素的公园卫星图,结合现实可到达情况,确定公园边界和湖泊边界.然后,在ArcGIS软件平台[2]中进行湖泊形态分区矢量化,分区结果如图1所示.采取分区处理的原因有两点:一是在中国古典园林理水艺术中,水景营造分为集中式布局和分散式布局[3],其中分散式布局将集中整体的水面分散开来,使其遍布全园形成水系,虽分散相连,但有相对独立的景观空间,从形态研究的角度来说,适合将整体化为局部区域提取形态再进行研究;二是组织湖面时,通常会使用桥、堤、岛等要素来分割水面,以丰富景观层次,扩大湖泊景观观赏范围,此时湖泊自然被划分成不同的独立区域,需要按独立区域提取形态再进行研究.因此,将整体湖泊形态在保持独立区域水域完整、视觉通视效果好的情况下进行分区.
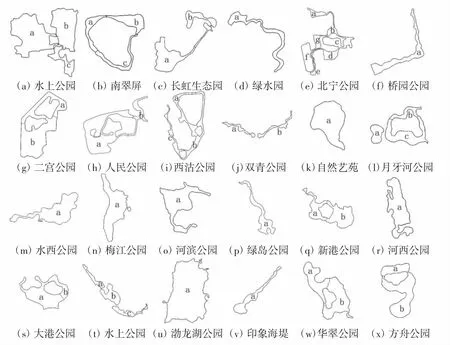
图1 湖泊形态分区处理结果
因此,本文以区域湖泊形态面积≥5 000 m2的42个样本为研究对象,进行湖泊形态数据收集与处理,各区域湖泊形态面积具体结果见表2.

表2 区域湖泊形态面积
2.2 数据转化分析
将ArcGIS软件平台的区域湖泊形态矢量化结果导入至Rhino+Grasshopper(下文简称“R+G”)参数化设计平台[4],进行湖泊形态定量数据的转化获取工作,并直接计算形态指标值.将形态指标值汇总至SPSS 24软件平台,对单一要素进行频率分析和正态分布,对2个相关要素建立回归模型进行回归分析.
3 湖泊形态定量指标及数据获取
3.1 湖泊形态定量指标
(1)湖泊面积(A):湖泊面积按水陆交接线所在位置圈定,体现湖泊的大小和规模.
(2)湖泊周长(P):指湖岸线长度,按水陆交接线所在位置划定,影响分形维数、近圆率等指标.
(3)湖泊最长轴(L):指湖岸线形态轮廓上距离最远两点连线的长度,影响形状率指标.
(4)形状率(FR)

形状率反映湖面的开阔程度和环流形成,是湖泊景观形态研究方面的常用指标.形状率较小的湖泊,湖面宽窄变化大,岸线曲率大、局部形状相对封闭[5].形状率较大的湖泊,一般湖面开阔,湖流通畅,不易形成死水区[6].
(5)近圆率(CR)

近圆率是将湖面形态和相同面积的圆作比较,体现空间的离散程度.湖泊形态近圆会使驳岸轮廓线趋于均质,导致湖泊景观缺乏空间变化,削弱其生态功能.湖泊形态的近圆率影响景深和岸线曲率,表现为近圆率越小,景深越大,岸线曲率越大[7].
(6)岸线发育系数(DL)

岸线发育系数用以描述湖岸的曲折程度,它将湖泊形态与相同面积的圆比较,以反映湖岸的曲折程度,其值越大则湖岸越曲折,是常用的湖泊形态指标[8].另外,该指标还与沉水植物和漂浮植物多样性呈显著正相关关系,影响生态效益[9].
(7)水体空间包容面积(ΔA)

公式中R代表面积相等的标准圆半径,R0代表最大外接圆半径.由于公园面积是一定的,所以湖泊面积和陆地面积成反比关系.城市中用地紧张,公园需要足够的陆地面积来发挥各种功能,但湖泊景观作为重要的兴趣景观,其景观效果不应只局限于公园的某一部分.在这种情况下,可以通过调整湖泊形态,扩大湖泊景观在公园景观中的控制范围,其控制范围反映为空间包容效应.ΔA指当湖泊面积不变、其形态改变时所增加的包容面积.通过优化城市综合公园湖泊形态,达到更好的空间包容效果,加强水陆空间的正向耦合效果.
(8)紧凑度(C)

公式中A代表湖泊面积,A0代表最小外接圆面积.紧凑度侧重反映湖面的开阔程度,其数值与湖面开阔程度成正比关系.
3.2 湖泊形态数据获取
湖泊形态数据传统的收集方法是按指标公式需要的值对每一个湖泊形态进行测量,再进行计算和统计,步骤繁琐且效率较低.本研究通过R+G参数化软件平台,以一种简单高效的方式完成从矢量图形到指标数据的转化.
具体方法为:将ArcGIS平台中的湖泊形态矢量化结果导入R+G平台,搭建“湖泊形态数据参数化收集”运算集,以泰丰公园c区湖泊形态为例运行运算.即拾取泰丰公园c区湖泊形态的矢量化线条,直接对湖泊的面积(A)、周长(P)、最长轴(L)进行数据提取.然后直接进入湖泊形态指标公式计算模块进行计算,得到湖泊形态的形状率(FR)、近圆率(CR)、岸线发育系数(DL)、水体空间包容面积(ΔA)和紧凑度(C)的计算结果,结果如图2所示.这种操作方式极大的简化了数据获取的步骤,提高了工作效率和精度.

图2 湖泊形态数据参数化收集运算集
将湖泊面积≥5 000 m2的42个区域湖泊形态数据汇总并进行指标统计,统计结果见表3,为数据分析做准备.

表3 湖泊形态指标数据统计表
4 湖泊形态指标数据分析
4.1 频率分析
图3为湖泊形态指标频率分析图.由图3可知,83.3%的湖泊面积集中于[0,50 000]的区间内,即本研究对5公顷以内的区域湖泊形态设计有较大的参考意义.另外,在[50 000,500 000]的区间内也有少量的样本分布,即本研究对大于5公顷,小于50公顷的区域湖泊形态设计也有一定的参考意义.

图3 湖泊形态指标频率分析图
90.4 %的湖泊周长集中于[500,3 000]的区间内.92.9%的湖泊最长轴集中于[0,1 000]的区间内.97.6%的形状率集中于[0,0.4]的区间内.92.9%的近圆率集中于[0,0.4]的区间内.90.4%的岸线发育系数集中于[2.5,6.5]的区间内.95.2%的水体空间包容面积集中于[0,650 000]的区间内,71.4%的水体空间包容面积集中于[0,150 000]的区间内.97.6%的紧凑度集中于[0,0.5]的区间内,76.2%的紧凑度集中于[0,0.35]的区间内.
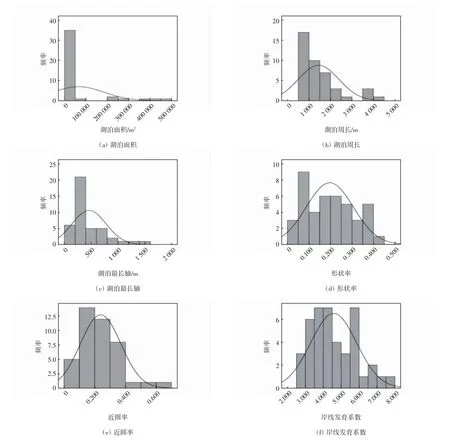
数值区间反映了天津综合性公园湖泊景观的形态特征,主要表现为区域湖泊多具有一定的开阔度,景深效果适中,空间格局紧凑度适中,湖岸线自然流畅,形态曲折变化丰富,水体空间包容效果好.形成视线通达、岸线自然、空间丰富的天津综合性公园湖泊景观,从而为公园整体景观增添魅力,提高游人观景游览兴趣度,有效加强自然景观与城市景观的联系.
4.2 回归分析
4.2.1 湖泊面积-湖泊周长
图4为天津综合性公园湖泊面积(A)和湖泊周长(P)的回归分析图,湖泊面积的sig值低于0.05,表明湖泊面积对岸线周长具有显著影响.对应的回归方程为:P=0.007A+980.585(R2=0.813).由图可知,随着湖泊面积的增加,湖泊周长也随之增加.因此,在进行综合性公园湖泊景观设计时,可通过扩大湖泊面积来延长湖岸线长度.

图4 湖泊面积-湖泊周长回归分析图
4.2.2 湖泊最长轴-湖泊面积、湖泊周长
图5、图6分别为天津综合性公园湖泊最长轴(L)和湖泊面积(A)、湖泊周长(P)的回归分析图.对应的回归方程为:A=322.83L-83 780.322(R2=0.725)、P=2.868L+122.857(R2=0.911).由图可知,湖泊面积随湖泊最长轴的增大而增大,湖泊周长也随湖泊最长轴的增大而增大.也就是说,湖泊最长轴同时控制影响着湖泊面积和湖泊周长.将图6与图4对比可知,相比面积,最长轴对湖泊周长的影响程度更大.因此,在进行综合性公园湖泊景观设计时,可通过设计湖泊最长轴长度来增加景深效果,延长游览路线,形成自然流畅的湖泊形态.

图5 湖泊最长轴-湖泊面积回归分析图

图6 湖泊最长轴-湖泊周长回归分析图
4.2.3 湖泊最长轴、湖泊周长-水体包容面积
图7、图8分别为天津综合性公园湖泊最长轴(L)、湖泊周长(P)和水体包容面积(ΔA)的回归分析图.对应的回归方程为:ΔA=815.417L-195 906.048(R2=0.866)、ΔA=250.62P-182.081.424(R2=0.739).由图可知,水体包容面积随湖泊最长轴的增大而增大,也随湖泊周长的增大而增大.由于图6反映了湖泊周长随湖泊最长轴的增大而增大,则可推出湖泊最长轴直接影响水体包容面积.结合前文可知,当湖泊最长轴在一定范围内增长时,湖泊面积、湖泊周长和水体包容面积同步增长,可以有效提高湖面占比,并加强水陆空间的正向耦合效果.因此,在进行综合性公园湖泊景观设计时,湖面最长轴应在范围区间内选择该值最大的湖泊形态.

图7 湖泊最长轴-水体包容面积回归分析图

图8 湖泊周长-水体包容面积回归分析图
4.2.4 岸线发育系数-近圆率、形状率
图9、图10分别为天津综合性公园岸线发育系数(DL)和近圆率(CR)、形状率(FR)的回归分析图.对应的回归方程为:CR=-0.093DL-0.663(R2=0.823)、FR=-0.66DL+0.499(R2=0.602).由图可知,近圆率随岸线发育系数变大而变小,形状率也随岸线发育系数变大而变小.数据表明岸线曲折度增大会延长景深,同时会加剧水面的宽窄变化.一定范围内岸线曲折度数值的增加可以使湖泊形态更明显、景观空间感更强.但是,当岸线曲折度数值的增加超出范围后,会导致湖面狭窄,影响环流,甚至形成死水区.因此,在进行综合性公园湖泊景观设计时,要控制岸线曲折度值的区间,不能一味追求形态变化而放弃湖泊景观的可持续发展能力.

图9 岸线发育系数-近圆率回归分析图

图10 岸线发育系数-形状率回归分析图
4.2.5 形状率-近圆率、紧凑度
图11、图12分别为天津综合性公园形状率(FR)和近圆率(CR)、紧凑度(C)的回归分析图.对应的回归方程分别为:CR=0.938FR+0.054(R2=0.611)、C=1.248FR+9.931×10-5(R2=0.996).由图可知,近圆率随形状率变大而变大,紧凑度随形状率变大而变大.也就是说形状率越大,湖泊形态越近圆且紧凑,会使湖面开阔,但也会使湖岸线均质单一、景深变小.因此,在进行综合性公园湖泊景观设计时,对主要节点的区域湖泊形态选择形状率范围内的较小值,确定面积宽广、形态变化丰富、湖岸线优美流畅的区域湖泊做主要水面.对次要节点的区域湖泊形态选择形状率范围内的较大值,确定面积相对较小、形态饱满的区域湖泊做次要水面,使整体湖泊形态达到收放自如的效果,避免湖泊形态出现过于曲折或者过于僵化的问题,实现大水面与小水面的平衡与配合.

图11 形状率-近圆率回归分析图

图12 形状率-紧凑度回归分析图
5 结果与分析
(1)湖泊形态要重视湖泊最长轴的设计.湖泊最长轴越大,加强画面景深的效果越好,同时延长游览路线,并有效提高湖面占比,加强水陆空间的正向耦合效果.当有多种湖泊形态方案时,可在范围区间内选择湖泊最长轴为最大值的方案,以形成自然流畅、空间丰富的湖泊景观.
(2)湖泊形态要控制岸线发育系数值.岸线发育系数在一定范围内增大可以强化湖泊形态,增强人的景观空间感受,还可以提高植物的多样性.但超出范围时,可能导致湖面过于狭窄,逐渐形成死水区.当有多种湖泊形态方案时,可在范围区间内选择岸线发育系数为最大值的方案.
(3)湖泊形态要控制形状率值.可对主要节点的区域湖泊形态选择形状率范围内的较小值,对次要节点的区域湖泊形态选择形状率范围内的较大值,使大水面与小水面、主要节点和次要节点有机组合,形成湖岸优美、空间丰富的综合性公园湖泊水系.
6 结语
本文对24个天津市综合性公园进行实地调研,以42个区域湖泊形态为研究对象,搭建“湖泊形态数据参数化收集”运算集对42个区域湖泊形态指标进行数据提取并汇总.通过对形态数据进行定量分析,挖掘各指标间的内在关系,找到对城市综合性公园湖泊景观设计有参考价值的形态指标.
城市综合性公园湖泊景观具有复杂性,其形态设计既需要依据本文所述的形态指标进行量化控制,为形态选择提供数据参考,也需要设计师依据现实情况和艺术审美进行综合调整,由此共同完成城市综合性公园优美流畅、运行良好的湖泊景观形态设计.

