Matlab在数学物理方程可视化教学中的探析

刘 彪 刘庆源 刘华勇

（安徽建筑大学数理学院，安徽 合肥 230601）

0 引言

偏微分方程在物理学、化学等自然科学和工程技术等领域都有着十分广泛的应用。在这些研究领域中经常出现很多描述某些物理规律的方程，称其为数学物理方程。对这些方程的求解，不仅可以得到一些有实用价值的结论，而且还可以促进这些领域的发展。数学物理方程课程的研究对象是3 类典型的偏微分方程——热传导方程、波动方程、位势方程。这些方程是在物理学、生物学、化学、工程学等自然科学和工程技术应用领域中产生的[1，2]。

数学物理方程课程是物理、声学和土木工程等理工科专业本科生的一门专业基础课，在实际教学过程中，学生反映课程难学，授课教师表示难教。主要原因有以下几个：（1）本门课程涉及的相关课程的知识点比较多。主要涉及的有高等数学、线性代数和常微分方程的知识，甚至有些章节还用到复变函数和泛函分析的知识点。（2）本门课程具有很强的理论性、计算量偏大。3 类经典方程求解的过程复杂，涉及知识点比较多，推导冗长，学生比较容易产生畏难心理。（3）学生理论基础较好，但是缺乏利用相关数学知识建模，进而解决实际问题的能力。作为数学理论知识与解决实际问题联系的一个非常重要桥梁，本课程具有很强的实际应用背景，是国内理工科大学很多专业的必修课之一。运用数学物理方程中的某些方法或理论解决实际问题，可使学生开阔眼界，进一步提高学生处理实际问题的能力，所以这就要求授课教师从教学内容、教学方法及教学模式等方面进行有效地创新，不断积极探索该课程与实际问题的关系，加强数学物理方程的教学与实际应用问题的衔接。

（1）在实际授课过程融入实际案例，比如，在讲解反应扩散方程时，介绍斑图形成的原理。能够激发学生学习数学物理方程的兴趣，提高学生推导计算能力，增强学生数学逻辑思维能力，进而提高学生解决相关实际问题的能力。

（2）提升数学理论知识的图形可视性，比如，反应扩散方程诱导斑图发生时的图形。随着数学软件的引入，数学问题的直观性就会得到充分展现。

（3）在实际教学中，针对不同专业的学生讲解内容侧重点不同。但是，重点不变的是与本门课程相关内容的实际物理背景以及凸显的基本数学思想。

利用Matlab 软件，对数学物理方程中的相关模型求解，可以使抽象、复杂的问题简单化、具体化、形象化，因此将Matlab 软件合理运用在教学过程中，可以降低教与学的难度，并通过对图形的直观认识和理解，更能激发学生的学习兴趣，调动学生的创造力，发挥学生的想象力。

1 反应扩散方程

反应扩散方程作为3 类经典物理方程之一，具有很强的实际应用背景。同时，反应扩散方程也可以解决许多实际问题，如各种动物的外表的形成，生物体的自组织反应，神经网络信息传播，刻画化学反应中反应物与抑制剂相互作用的过程[3]。本节将给出几个反应扩散方程并利用Matlab 软件仿真系统不同时间时，时空解的演化趋势。

第一，二维复Ginzburg-Landau 方程[4]

ut=（1+iv）Δu+u-（1+iμ）u|u|2，其中（x，y）∈Ω=[0，100]×[0，100]，v，μ 为参数，令v=0，μ=1.5，边界条件为周期边界条件，初值为u（0，x，y）=（ix+y）exp（-0.03（x2+y2））。

图1 （a）表示系统的螺旋解（b）表示系统产生破缺现象（c）表示系统发生了混沌现象

第二，二维Gray-Scott 方程[5]。

ut=ξ1Δu+b（1-u）-uv2，vt=ξ2Δv+dv+uv2，其中，（x，y）∈Ω=[0，2]×[0，2]，ξ1=0.00002，ξ2=0.00001为扩散系数。初值为u（0，x，y）=1-exp（-80（（x+0.05）2+（y+0.02）2）），v（0，x，y）=exp（-80（（x-0.05）2+（y-0.02）2））。边界条件为周期边界条件。

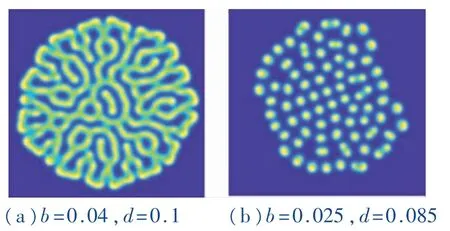
图2 （a）系统在t=3 500 时的Rolls 解，（b）系统在t=3 500 时的点状解

第三，一类具有随机Gaussian 分布项的捕食食饵模型[6]

第四，具有Beddington-DeAngelis 功能反应函数的超扩散反应捕食食饵模型[7]

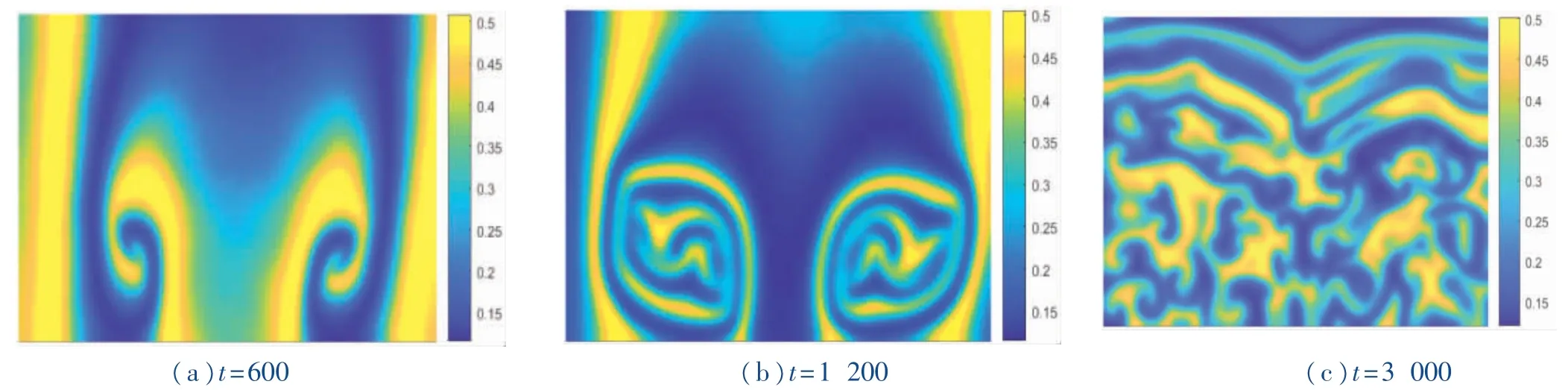
图3 系统发生Hopf 分支时，时间周期解的演化过程

图4 参数在Turing-Hopf（余维-2）分支点附近选取时，分数阶算子指数对系统时空周期斑图的影响

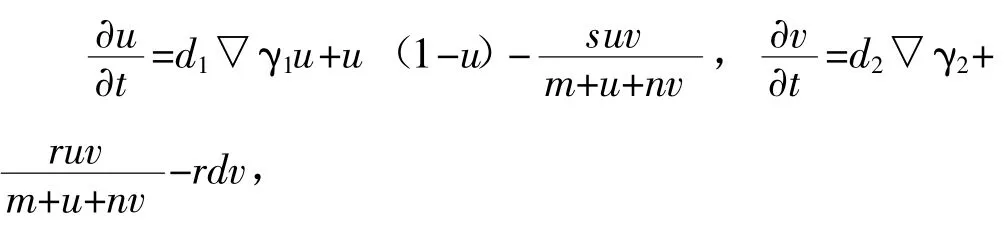
式中：▽γ 为分数阶Riesz 算子，γ∈（1，2）边界条件为Dirichlet 条件。参数取值分别为s=1，m=0.01，n=0.5，d=0.5，d1=0.2。当d2=2.923，r=1.555 6 时，系统发生余维-2 的Turing-Hopf 分支。（u0，v0）=（0.1+10-3（cosx+cosy），0.18+10-3（cosx+cosy））。

2 结语

本文以反应扩散方程为例，介绍了几类方程在不同边界条件下，选择合适的参数时，数值仿真实现了系统时空解的演化趋势的可视化教学，所以在实际教学中适当引入Matlab 软件，能够帮助学生更好地掌握数学概念、理解几类边界条件和时空解的内涵、逻辑推演等，可有效地激发学生学习数学物理方程的积极性和创新性，进一步扩展拓展学生的数学思维和逻辑推演能力。同时Matlab 等软件的使用有助于激发学生学习的主观能动性，更有利于教师探究性学习和翻转课堂教学模式的开展；可以让教师的教和学生的学，更加关注物理图像背后的概念与思想，实现领悟数学物理方程的思想。