基于小波包能量谱的工业机器人智能故障诊断
李振东,李先祥,周星
(1.佛山科学技术学院机电工程与自动化学院,广东佛山 528000;2.顺德职业技术学院人文学院,广东佛山 528000;3.佛山智能装备技术研究院,广东佛山 528000)
0 前言
工业机器人长期以来一直被用于生产系统,以提高自动化制造过程中的生产率、质量和安全性。然而在生产线上,随着工业机器人运行时长的不断增加,工业机器人出现故障的概率也随之增加,不同原因的故障导致的工业机器人意外停机有可能导致整个生产线中断,从而造成经济和生产损失。因此,为保证工业机器人在自动化产线中正常运行,研究工业机器人的故障诊断具有非常重要的意义。
传统工业机器人系统和非工业机器人旋转系统[1]中机械故障以振动信号分析为主。然而,振动信号分析的准确性和有效性对传感器位置和环境噪声非常敏感[2]。此外,当安装的传感器出现故障时,需要机器人停机检查和更换传感器,这将会造成额外成本和非计划停机。
最近,电流信号在各种旋转机械关键部件的故障检测中被证明是准确且经济有效的,如电机[3-5]、齿轮箱[6]和轴承[7]、减速机[8]。与振动信号相比,工业机器人系统和伺服驱动器之间的电流信号获取简单方便,而且不需要额外传感器,也不会入侵机器人的系统。基于反馈电流信号的工业机器人故障诊断需要解决2个关键问题:(1)故障特征提取,即提取不同故障类型的有效特征;(2)故障识别,即根据故障特征定位故障轴。特征提取可以提高故障诊断的性能已被证明。时域分析方法用来提取峭度和均方根等特征作为关键部件的状态特征。频域分析方法用于揭示时间序列信号中隐藏的频率信息等特征。还有时频域分析方法,如短时傅里叶变换[9]和希尔伯特-黄变换[10],能够提取频率分量并保留时域信息。然而,这些方法存在一些局限性,如故障特征和噪声干扰仍然难以有效分离。在故障识别方面,深度学习掀起了智能故障诊断的热潮,基于深度学习智能诊断的模型包括深度自动编码器[11]、深度信念网络[12]、CNN[13]。其中,CNN由于其独特的共享机制,大大减少了网络参数的数量,在工业界得到了广泛应用。
综上所述,提出一种非入侵式的采集方式,通过采集工业机器人运行时的反馈电流进行故障检测。采用反馈电流的优点在于:(1)采集方便,可以定时、定量、定运行动作采集数据;(2)外界干扰小,噪声和其他干扰对数据影响小。因此,本文作者提出一种基于WPES-CNN的故障诊断方法,用于反馈电流检测工业机器人的运行状态。首先,对反馈电流原始信号进行小波包分解与能量特征提取;然后,建立CNN诊断模型,从小波包能量谱中自动提取代表性的特征,实现故障分类。
1 小波包-卷积神经网络的构建
小波包分析是小波分解的进一步改进,具有良好的时频局部化的功能,可以将电流信号分解到各个子带中,从而凸显故障信息,易于故障特征的提取,而且能够把信号分为高频和低频信号,这种分解既无冗余,也无疏漏。所以,小波包分析在处理工程实际问题中就显得尤为重要。
1.1 小波包定义
根据小波包的定义式,给定尺度函数φ(t)和正交小波函数ψ(t)的二尺度关系:
(1)
其中:h(k)为对应的低通滤波器;g(k)为对应的高通滤波器;式(2)为推广的二尺度方程:
(2)
式(2)中定义的函数系{μm(t)|n∈Z}称为由尺度函数φ(t)所确定的正交小波包。
1.2 小波包分解
信号x(t)的小波包变换就是在L2(R)子空间S(0,0)进行分解得到A、D。只要用于分解的滤波器为一组共轭正交滤波器组,则小波包分解式:
S=A(j+1,2n)⊕D(j+1,2n+1)
(3)
小波包分解的一般表达式:
S=A(j+1,0)⊕D(j+1,1)=
A(j+2,0)⊕D(j+2,1)⊕A(j+2,2)⊕
D(j+2,3)=
⋮
A(j+k,0)⊕D(j+k,1)⊕…⊕A(j+k,2k-
2)⊕D(j+3,2k-1)
(4)
图1所示为k=3的小波包分解的过程。其中A表示信号的低频部分,D表示信号的高频部分,第一位数字表示小波包分解的层数。
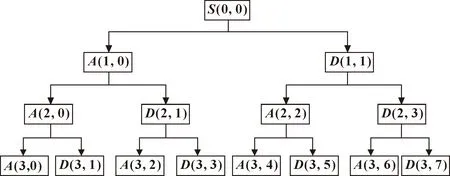
图1 三层小波包分解示意
1.3 小波包能量谱
一般来说,通过第1.2小节小波包的分解,将原始信号中的信息分解到不同的子频带中,而且原始信号经过小波变换过程中的能量守恒,当工业机器人出现故障时,就会影响每层子频带能量的分布,然后学习不同故障的分布特征,进而达到故障识别,因此,小波包能量可以表示工业机器人健康特征。其第j层第i频带的相对频带能量Ei可以表示为
(5)
其中:j为层数,i为该层的第i个频率带,若j=3层,则i=8段;E为频带的总能量。
在实际处理中,由于工业机器人反馈电流的采样频率为 250 Hz,低频段能量较大,占总能量的比值较大,因此在处理运算过程中对能量Ei做整体开方运算,以适当提升高频段数值大小,得到的能量特征如下:
(6)
1.4 小波包能量谱转化为二维矩阵
由于卷积神经网络在处理图像方面具有很大优势,因此文中提出一种将小波包能量特征转化为二维矩阵的方法。具体方法分为3个过程:首先,利用小波包变化将原始信号分解为多个频率段;然后将每个频率段(如第1.3节方法)转化为能量谱;同时为了提高卷积神经网络的分类精度,将每段能量谱值转化为一个二维的m×m的矩阵,如图2所示。

图2 二维矩阵转换过程
1.5 CNN神经网络
CNN(Convolutional Neural Networks)具有权值共享、稀疏连接等优点。与传统的神经网络相比,CNN大大减少了可训练参数的数量,从而实现了更深层次的网络架构。CNN网络模型主要有3部分:卷积层、池化层和全连接层。
卷积层是CNN的主要组成部分,它将输入特征矩阵与几个可训练的核进行“卷积”,并生成相关的特征图。在卷积层,使用一组可学习的高斯核滤波器对输入数据进行卷积,生成特征映射,可以表示为
(7)

池化层是为了降低特征图的维度,对卷积层的输出进行“下采样”。选择一个可定制的池操作窗口,将它滑动到输入特征图上,指定操作区域,然后用数值统计方法表示这些值,并降低所选区域的分辨率。最大池化通常应用于CNN结构中,最大池化卷积核的大小一般是2×2。非常大的输入量可能需要4×4。但是,选择较大的形状会显著降低信号的尺寸,并可能导致信息过度丢失。通常,不重叠的池化窗口表现最好。
全连接层在整个卷积神经网络扮演“分类器”角色。如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话,全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。
1.6 小波包-卷积神经网络模型
文中提出了WPES-CNN (Wavelet Packet Energy Spectrum- Convolutional Neural Networks)智能故障诊断方法,用于反馈电流检测工业机器人的运行状态。提出的方法流程如图3所示,一般程序总结如下:

图3 小波包-卷积神经网络模型
(1)工业机器人关节电流信号由伺服驱动发出,采集脚本进行采集,保存到工业机器人的控制器中;
(2)将原始数据进行周期性提取,目的是使机器人运行动作保持一致;
(3)对提取的周期数据进行小波包能量谱的特征提取;
(4)在小波包能量谱的基础上,将它转化为二维矩阵,在没有任何手动情况下,该二维矩阵被分为训练样本和验证样本;
(5)用一系列训练样本构造CNN,然后用于训练样本的无监督特征学习;将学习到的特征输入Softmax分类器,用于工业机器人故障模式识别;
(6)使用验证样本验证所提出方法的性能,并报告诊断结果。
2 实验数据及结果分析
文中使用国产机器人企业的六轴工业机器人运行时产生的反馈电流故障数据集来评估所提出方法的有效性,实验装置如图4所示。通过计算机连接机器人的控制器将数据采集脚本下载到控制器中,当机器人运行特定程序时会触发采集脚本进行数据采集,采集的数据由伺服驱动提供,最后通过云平台或者手动将数据拷贝出来。采样频率250 Hz。实验数据包括工业机器人4种工况下的电流信号,分为:正常信号、1轴减速机故障信号、3轴减速机故障信号、4轴减速机故障信号。

图4 实验装置
2.1 数据集
在数据收集过程,工业机器人运行相同动作,同时采用部件替换实验获取机器人多故障数据,原始数据样本集分布见图5。数据集分类类别见表1。

图5 正常信号与故障信号的时域

表1 数据样本集
小波包特征提取通过从原始数据中随机选取长度1 000作为一个样本,每种工况提取3 000个样本。小波包特征提取的样本集如表2所示。小波包分解系数的节点能量谱如图6所示。
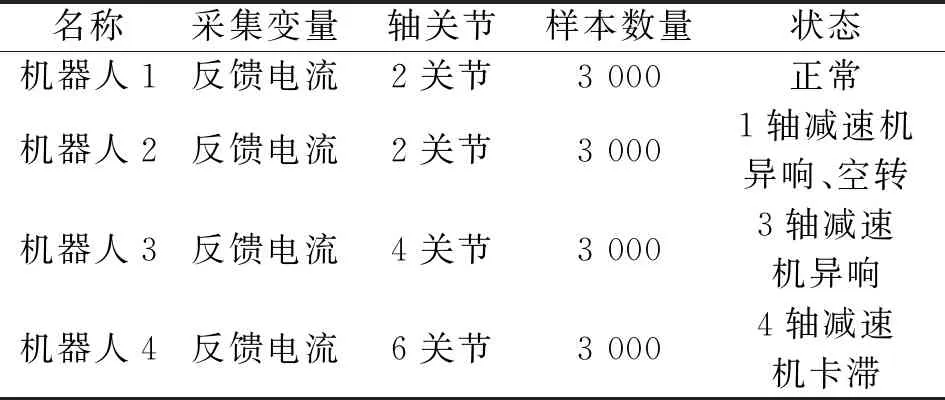
表2 小波包特征提取的样本集

图6 小波包能量谱特征
样本分布按照训练集:测试集=7∶3,验证集包含在测试集中。训练集:每种工况随机选取2 100个样本作为训练集,训练集共包括8 400个样本;测试集:剩余的样本集作为测试集,每类900个样本,测试集共包括3 600个样本。
2.2 结果分析
2.2.1 CNN的输入矩阵形状对结果的影响
对原始信号进行4层小波包分解,并将分解系数进行能量归一化操作,由于CNN在处理图像时有着独特的优势,文中在将能量特征输入CNN模型前进行矩阵转化,过程如第1.4节所述,文中测试了5种矩阵形状对结果的影响,分别是:1×16、2×8、4×4、8×2、16×1,结果如图7所示。图7给出了不同形状下验证集的识别准确率(3次实验取平均值,下同)。可知:输入矩阵为方阵(4×4)的效果最好。
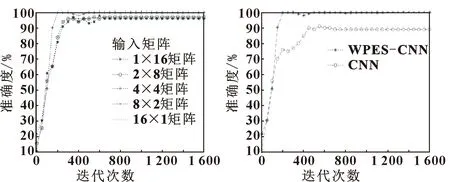
图7 输入矩阵形状对结果的影响 图8 2种方法验证结果
2.2.2 WPES-CNN 与CNN识别结果对比
CNN故障诊断模型使用的训练集和测试集是第2.1小节中未经过特征提取的数据集,样本长度同样是1 000,样本数量为3 000。最后将样本按照7∶3的方式输入到CNN模型中进行故障识别,2种方法的识别结果如图8所示。可知:没有经过特征提取的CNN诊断模型的验证精度仅为92%。
为了进一步验证WPES-CNN方法的优越性,将支持向量数据描述(Support Vector Data Description,SVDD)、CNN网络和BP网络预测结果与它进行比较,比较结果如表3所示。其中基于SVDD模型的诊断平均准确率为83.6%,采用CNN模型的诊断平均准确率为91.3%,采用BP网络的诊断平均准确率为89.9%,均小于WPES-CNN网络的故障平均准确度99.9%,说明采用WPES-CNN方法能够有效提高对故障类别的识别准确率。
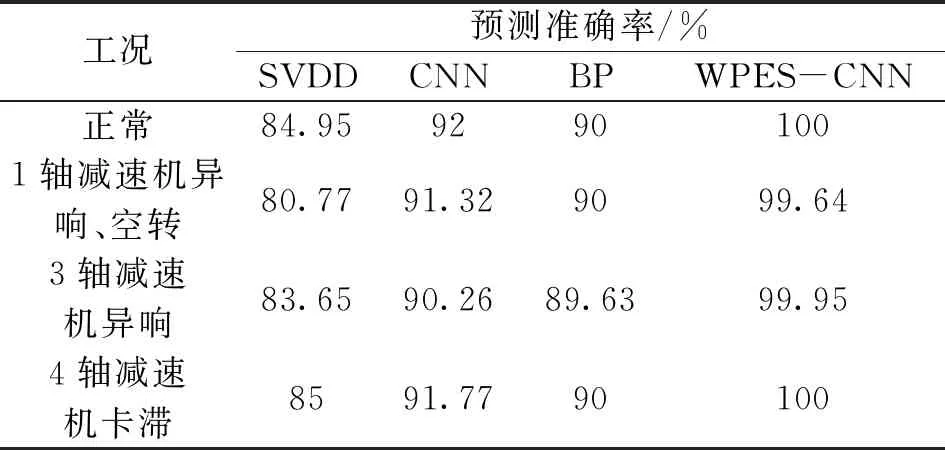
表3 多种识别算法的预测准确率对比
3 结论
文中提出了一种非入侵式WPES-CNN故障诊断方法,对反馈电流信号表征工业机器人的健康状态进行了深入分析,得到了反馈电流随着机械臂减速机不同故障类型的能量特征,为反馈电流应用于机械臂减速机状态监测提供了基础。首先,文中通过小波包分解方法对反馈电流时域信号进行处理,分解得到4层小波系数;其次,结合电流信号的能量随着减速器故障程度会变化的规律,建立能量特征库;然后,将输入能量特征转化为方阵,提高模型的准确率;最后,将方阵特征作为CNN的输入,相较于SVDD、BP和CNN诊断模型,WPES-CNN的故障识别率达到99.9%,验证了所提故障诊断方法的有效性。为工业机器人健康状态监测提供了一种新的思路,而且经济有效,非常有应用前景。

