基于模糊认知图的轴承故障诊断方法研究

韩光信，甘群丰，于天暝，陆洋，胡云峰

(1.吉林化工学院信息与控制工程学院，吉林吉林 132000；2.东北电力大学自动化工程学院，吉林吉林 132000；3.吉林大学通信工程学院，吉林长春 130000)

0 前言

滚动轴承被广泛应用于现代工业，是旋转机械的关键部件之一。滚动轴承故障诊断不仅可以保证机械设备的平稳性和有效性，而且有利于及时发现和排除意外故障。滚动轴承故障诊断在一定程度上能防止重大事故的发生，具有重要意义。通常，由于轴承工作环境的限制，无法直接进行诊断。传感器可用于收集能够反映轴承状态的数字信号，如光谱信号、声音信号和振动信号。频谱信号和声音信号可用于无损探伤，具有特征频率明显、故障早期预测性好的优点。然而，这些方法对设备和操作员的专业素质要求很高。轴承的振动信号包含丰富的故障能量信息，轴承振动信号的采集不需要复杂的设备和专业人员。然而，传感器采集的数据规模巨大，如何快速、有效地识别故障成为了一个难题。因此，提出将轴承故障数据按照既定的标准进行等量分割，利用专家经验对片段进行识别与标注，并创新性地把轴承故障诊断问题建模为时间序列分类(Time-Series Classification，TSC)问题。通过提取异常数据和正常数据的特征，达到识别异常数据的目的。

时间序列分类的研究已经发展了20多年，许多算法得到了发展和广泛应用。TSC方法大致分为4大类：基于距离的、基于特征的、基于集成的和基于深度学习的模型[1]。在基于距离的时间序列分类方法中，将最近邻分类器与距离函数相结合是一种最常见的组合方式。当与最近邻分类器一起使用时，动态时间扭曲(Dynamic Time Warping，DTW)距离被证明具有非常强的基线[2]。LINES和BAGNALL[3]比较几种距离度量方法，结果表明没有一种距离度量方法明显优于DTW。基于特征的方法，通过提取原始时间序列中的有效特征进行分类，例如SFA符号包(BOSS)[4]、时间序列林(TSF)[5]。但是，这些方法存在一定的局限性，不能很好地利用提取的有效特征。近年来，一些研究者开始关注集成方法，它优于传统方法。BAYDOGAN等[6]提出了一个基于特征包表示的时间序列分类框架，通过概率估计将位置信息集成到一个紧凑的码本中，该方法具有较好的分类效果。BAGNALL等[7]提出将多维度的数据空间转换成一维数据，通过简单的集成方案来提高精度。虽然这些方法已经达到了较高的精度，但由于计算复杂度较高，无法应用于大型数据集。目前，深度学习也被广泛应用于TSC。KOH等[8]提出了一种改进网络的匹配学习算法，它在反向传播路径中使用了梯度路由。YU等[9]提出了各种形式的RNN自动编码器，作为时间序列的特征提取器。上述这些方法取得了良好的效果，但也面临着高维、复杂动力学的问题。目前，一种基于模糊认知图的时间序列的分类方法被提出，该方法表现出了更好的分类性能[10]。

这种方法的主要思想是将时间序列转换成FCMs的权重矩阵进行表征。FCMs的特征提取方式与以往一些经典特征提取方式(经验模态分解、小波变换等)有所不同，以往的方式在获取轴承信号特征分量后，需要进一步提取，以去除不相关和冗余的特征，而FCMs所学习的权重矩阵是专有的，无需进一步处理。FCMs具有简单直观的知识表示方式、非线性特性、可解释性、模糊性等优点，可以利用因果关系提高分类效果。然而，文献[10]中所提出的方法存在局限性，在面对包含噪声的数据集时，模糊C-mean聚类算法与梯度下降算法相结合的方式不能有效地提取数据特征。因此，提出利用奇异谱分析(Singular Spectrum Analysis，SSA)将原始时间序列扩展到高维空间，并实现降噪处理；利用凸优化算法(Convex Optimization，CVX)快速训练FCMs模型；利用BP神经网络(Neural Networks，NN)进行分类，并将该方法称为SSA-FCMs-NN。

1 背景知识

模糊认知图是神经网络与模糊逻辑两者结合的产物，模糊认知图有和神经网络相似的拓扑结构，是一种带反馈环的权重有向图，它利用概念节点和权重边描述物理系统的特性。如图1所示，一个典型的FCMs由概念节点和节点之间的有向边的权重组成，概念节点可以表示系统中的行为、实体、原因等，有向边权重代表节点之间的关联程度。

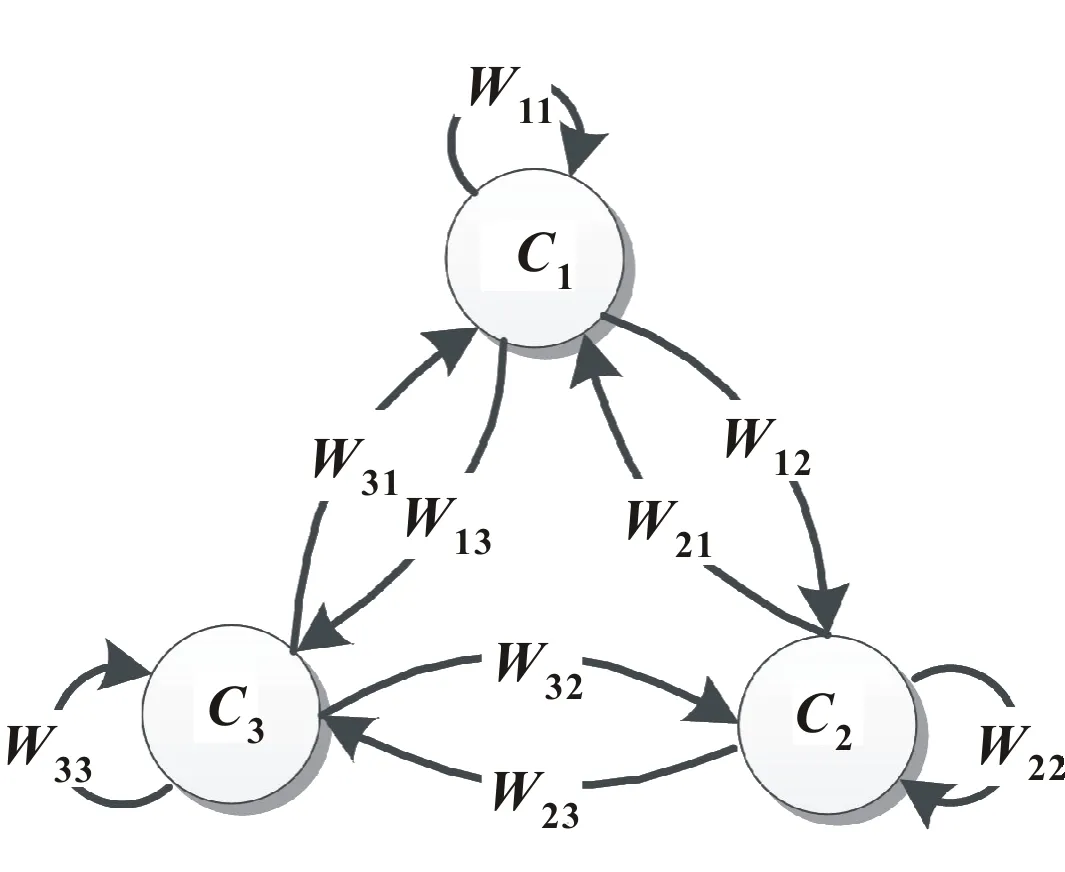
图1 一个典型的FCMs

标准FCMs所蕴含的语义可以由一个4元组U=(C,W,A,f)表示[11]，其中：C=[C1,C2,…,Cm]为m个概念节点的集合；m为概念节点的个数；W为m×m维的权重矩阵：

其中：Wij为概念节点Ci和Cj之间的因果关系的权值，Wij∈[-1,1]，其值的正负号与大小分别反映概念节点间因果关系的影响方向和程度，Wij>0表示概念节点Ci增加时Cj也跟着增加，Wij<0表示概念节点Ci增加时Cj反而减小，Wij=0表示概念节点Ci和Cj之间没有因果联系；Ai(t)为节点Ci在t时刻的状态值,该值是变动的；f为阈值函数，它是一个非线性单调递增的函数，将与目标节点有关联的所有节点的输入状态值整合到激活函数的定义域内。Cj在t+1时刻的状态值可通过以下公式计算：

(1)

常用的激活函数有Sigmoid函数：

(2)

双曲正切函数：

(3)

其中：Sigmoid函数将节点的状态值限定在区间[0,1]； 双曲正切函数将节点的状态值限定在区间[-1,1]；ξ>0决定了阈值函数的陡峭程度。

2 SSA-FCMs-NN算法

将轴承故障时间序列按照预定规则进行等量分割，产生样本集，如下所示：

(4)

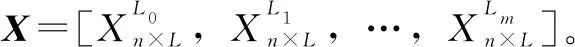
(5)

f-1[Ai(t+1)]=A(t)Wi

(6)

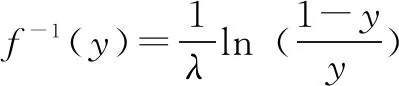
Yi=ZWi

(7)

FCMs的学习问题最终可以转化为约束最小二乘法问题[12]。为求解权重Wi，目标函数可表示为

(8)

图2 SSA-FCMs-NN算法流程

3 实验结果分析

使用分类准确率和科恩的卡帕系数评估SSA-FCMs-NN算法的性能。分类准确率公式如下所示：

(9)

其中：UT为测试样本的总数；Nerror为分类错误样本的数量。

评估给定分类器的性能并不是一件简单的任务。如果一个或多个类别预测失败，总体的分类并不能有效地评价模型的性能。另一个常用于多分类器基准测试的方法是科恩的卡帕系数。Kappa是分类变量之间一致性的指标，一般认为它比简单的百分比一致性计算更可靠，其公式如下：

(10)

其中：p0为评估者之间相对观察到的一致性；pe为偶然条件下的一致性。

在文中，应用K-fold cross-validation提高模型的拟合能力，其中K=3。分类准确率和Kappa的值取的是3次测量值的平均值。由于概念节点数、SSA嵌入维数L的不同和β的值都会影响最后的输出结果，默认选取最好的一组结果。

3.1 实验数据与参数设置

为验证所提出的SSA-FCMs-NN算法在轴承故障诊断中的有效性，利用广泛使用的轴承故障数据集进行对比实验，利用不同尺寸和功率产生4组实验数据。

数据集A、B分别来自0、735 W工作负荷，采样频率为12 kHz驱动端的振动信号，包含3种损坏尺寸(0.177 8、0.355 6 、0.533 4 mm)的内圈、外圈、滚动体的9类故障，以及1个正常基准，一共10类。

数据集C：将损坏大小固定为0.355 6 mm，并选择3种故障类型。每种故障类型有3个电机负载。然后，得到9类方位断层。一共得到9类采样频率为48 kHz驱动端的振动信号。

数据集D：将故障类型固定为滚动体故障，并调整损坏大小和电机负载。3种载荷(0、735、1 470 W)和3种损坏尺寸(0.177 8、0.355 6 、 0.533 4 mm)组合了9类轴承故障，采样频率为48 kHz，采集驱动端的振动信号。

上述的数据集A、B有10种方位状态，数据集C、D有9种方位状态，将数据集A、B、C、D等距离切割,其中数据集A、B一个样本中包含4 060个时间节点；C、D一个样本中包含8 125个时间节点；数据集A、B周期为406 r/s，数据集C、D周期为1 625 r/s，采用重采样的方式生成样本。数据集A、B中均包含2 800个样本和10个类别，每个类别有280个样本数；数据集C包含2 025个样本和9个类别，每个类别有225个样本；数据集D包含1 215个样本和9个类别，每个类别包含135个样本。

3.2 结果分析

3.2.1 SSA分解与时间成本分析

SSA可以分离时间序列中的复杂噪声，属于信号加噪声模型。图3所示为通过SSA对轴承故障数据进行特征提取的结果，可知时间序列的周期、振荡、趋势以及噪声等特征。

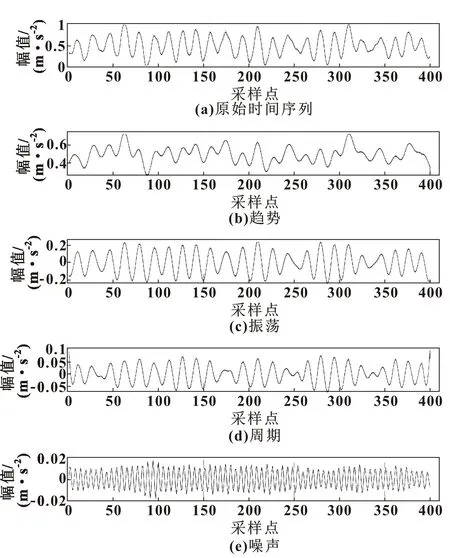
图3 原始波形与重构序列

粒子群优化算法(Particle Swarm Optimization，PSO)是依赖随机搜索的算法，每个粒子都会在多维搜索空间不断通过跟踪两个“极值”来更新自己，以寻找到最优值，但是它具有一定的盲目性，且效率低。为验证CVX算法的时间成本，对比PSO和CVX算法的时间成本，结果如表1所示。可知：与PSO相比，在同一个处理阶段，CVX算法时间成本仅为PSO的1/6。

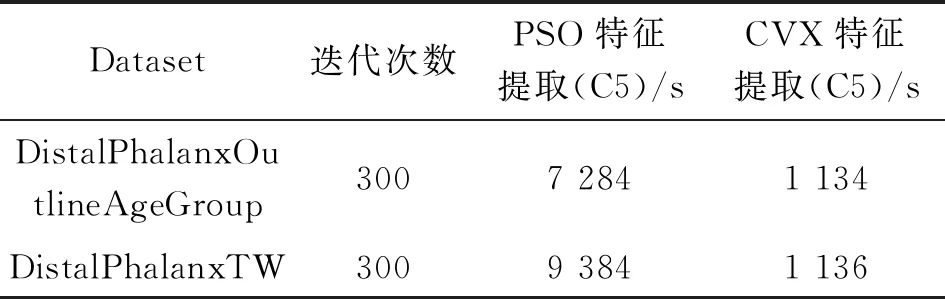
表1 PSO与CVX训练时间成本

3.2.2 概念选择与对比实验

为评估所提出的SSA-FCMs-NN算法的性能，分析SSA-FCMs-NN的几个参数对实验结果的影响。

如图4所示，在不同的数据集下，正则化参数所取得的值也不尽相同，正则化参数的选取是经过大量实验所得出的。在β=0.5和β=0.8取值下，能够获得一个较好的分类精度。还能够观察到概念节点的大小，也会直接影响结果。由图4(b)可知：当C=4时，精度最低，认为丢弃了的分量包含有效的特征；C=8时，精度最高，随后开始下降。由图4(d)可知：随着概念节点的增加，精度也随之增加，在C=6时，达到了最高值，之后精度在一定范围内振荡，可以认为SSA将原始时间序列分解为10个分量，提取前6个分量，实现了最大特征的提取和噪声的滤波。由图4(c)可知：C=8和C=9时，精度几乎相同，在考虑计算成本的情况下选择较小的概念节点。图5所示为Kappa值，它的变化基本与精度的变化趋势一致。

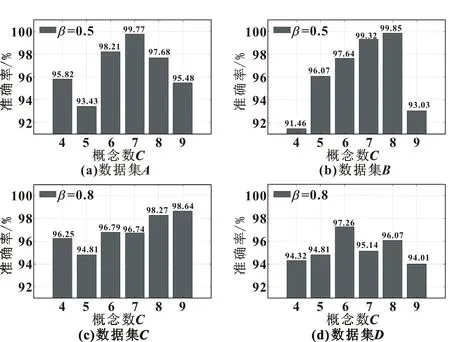
图4 SSA-FCMs-NN的精度与概念数C的关系

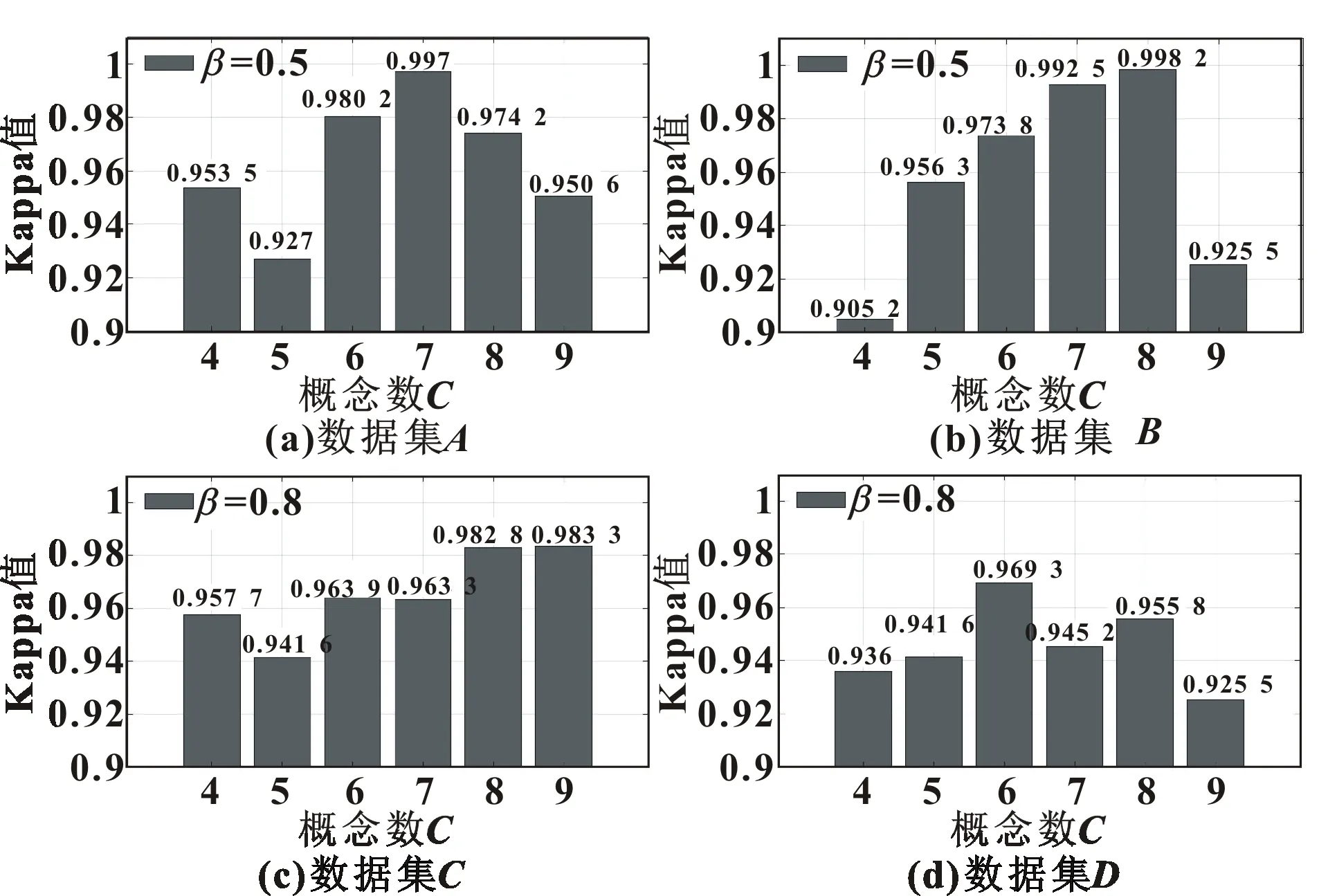
图5 SSA-FCMs-NN的Kappa值与概念数C的关系

选择近年相关文献[14-15]，与所提算法得出的实验结果进行比较，结果如图6和表2所示。由图6可以看出：文献中所提方法的故障分类准确都达到了98%以上，与SSA-FCMs-NN算法得出的实验结果所差较小 。由表2可知：浅层模型(OKL、SVM、SBELM、RF)的精度比深度模型(TSTFT-CNN、MC-CNN)低很多，这意味着深度学习技术对于多种故障类型的诊断具有更好的性能，深度模型可以提取一些潜在的特征；在4个浅层模型中，OKL比其他3个模型(SVM、SBELM和RF)具有更好的精度；在数据集C中，所提出的SSA-FCMs-NN算法比SDIAE方法分类准确率高2.51%，在数据集D中，精度相差不大。

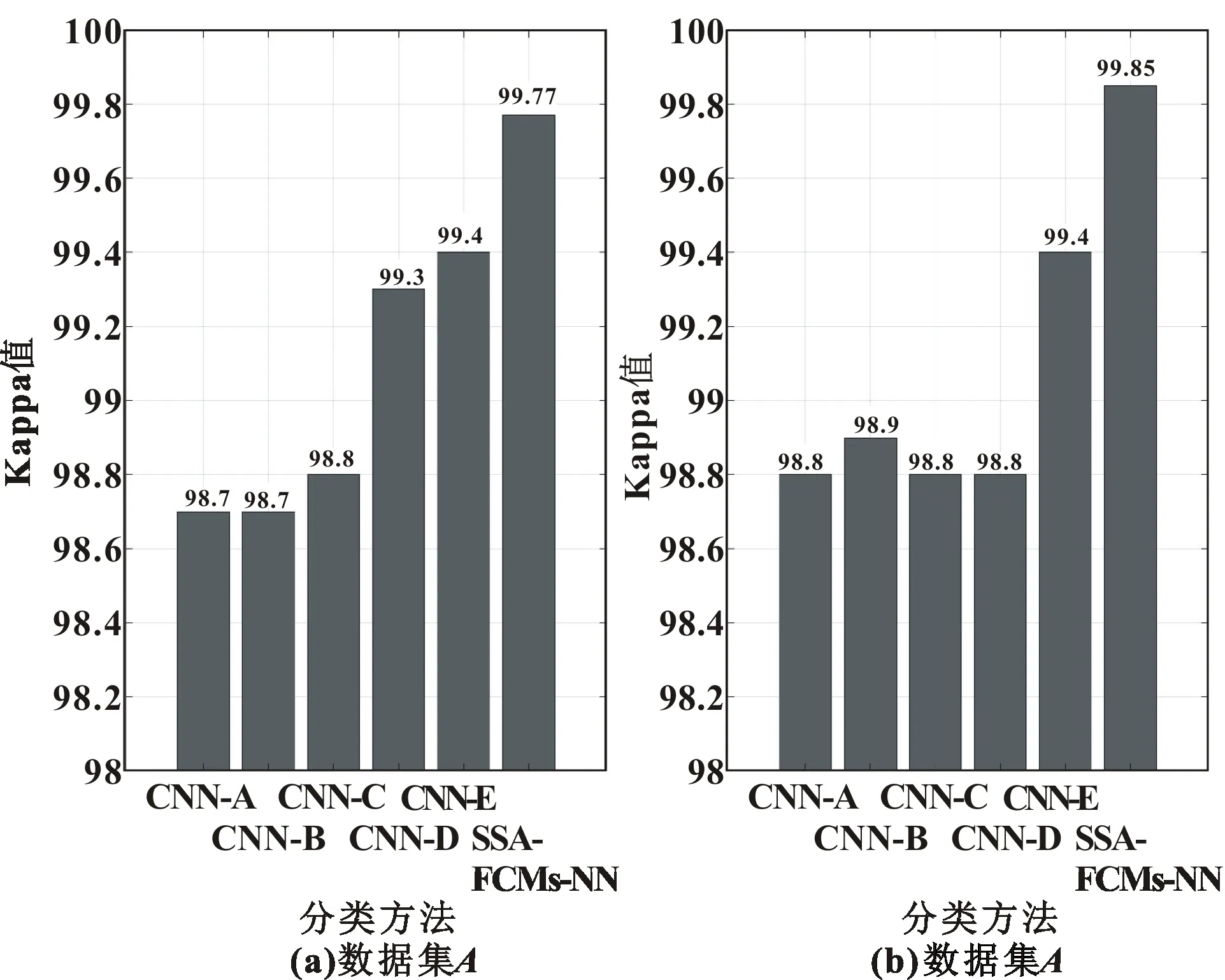
图6 SSA-FCMs-NN与其他先进算法的比较

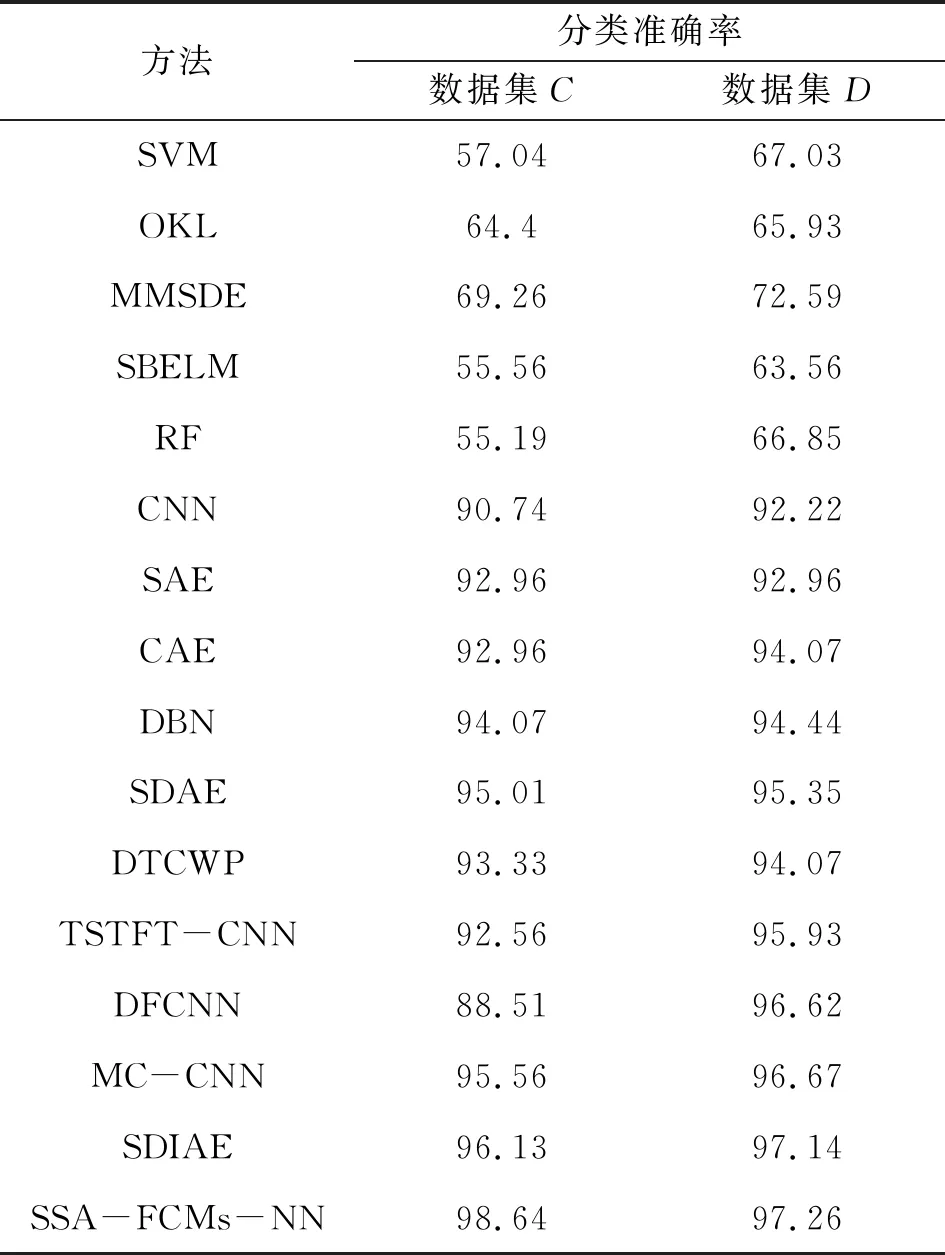
表2 SSA-FCMs-NN与其他先进算法的比较 单位：%

4 结束语

针对传统方法无法有效、快速地处理含噪声数据，提出了SSA-FCMs-NN算法。对比了PSO与CVX算法的训练成本，并分析了SSA的重构数据以及概念点的选择；通过对比近年相关的文献说明所提算法的优越性。