大数量级难加工小孔零件数控加工工艺分析及切削参数优化研究

刘冉冉,宁玲玲,郑健

(山东工程职业技术大学智能制造学院，山东济南250200)

0 前言

据统计,孔加工约占机械加工总量的1/3,占械加工时间的1/4。在孔加工中尤其以小孔的加工最为困难，一直是困扰数控工程师的难题。通常将孔径在(0.5～3)mm内的孔统称为小孔[1]。大批量的小孔加工由于其孔径小、排屑困难、加工噪声小，无法通过声音和振动判断切削情况进而调整参数，造成了小孔加工效率特别低、易断刀、易报废。针对以上问题，以振动分离筛为加工对象，通过实验加工密集的1.5 mm小孔，分析其加工切削参数在不同区间的适用范围，找出最佳的切削参数，在此基础上规划出连续加工可行区间。通过实验数据拟合出转速(S)、进给速度(F)、退刀量(R′)和切削结果之间的关系，为此类产品的加工提供参考。

1 工件分析

实验中选用的振动分离筛如图1所示。该工件用于自动化生产线中，它整体为不规则凹曲面壳体，侧面为不规则面。整体尺寸为122 mm×70 mm×45 mm，壁厚3 mm，底部有367个大小为1.5 mm的圆孔，要求小孔的孔径公差为0.027 mm、表面粗糙度为0.35 μm，与基准孔的同轴度为0.03 mm。此工件的加工难点主要在于薄壁零件难夹持，在加工过程中易变形、曲面难加工，最大的问题在于367个1.5 mm小孔的加工。钻削时切屑常常堆积在所加工部位的周边，一方面降低加工质量，另一方面随着加工的进行，加工效率不断降低[2]。按照正常的加工工艺耗时特别长，如果牺牲刀具寿命进行加工，很可能会由于磨损严重而不清楚具体的损坏时间，造成加工超差或者工件损坏。因此，找到一个理想的，速度快、质量好并且加工稳定的切削参数是此次实验的目的。

图1 振动分离筛模型

以该工件为实验载体，进行小孔连续加工实验，得出在此类小孔产品加工中最佳的切削参数。在实验前还需要规划合格的加工工艺，以达到最接近实际加工的场景。

2 工艺分析

表1所示为具体加工工艺。加工该零件需要首先考虑孔的加工，从图1(b)可以明显看出，该零件的孔不在一个平面上，特别是槽里面的孔只能在还没有加工出凹槽之前打穿。为了让切削参数具有说服力，不能采用经验法，所以通过计算得到基础的数据。根据上述已知条件，可以通过需要的刀具大小和精度要求得到理论的切削参数。

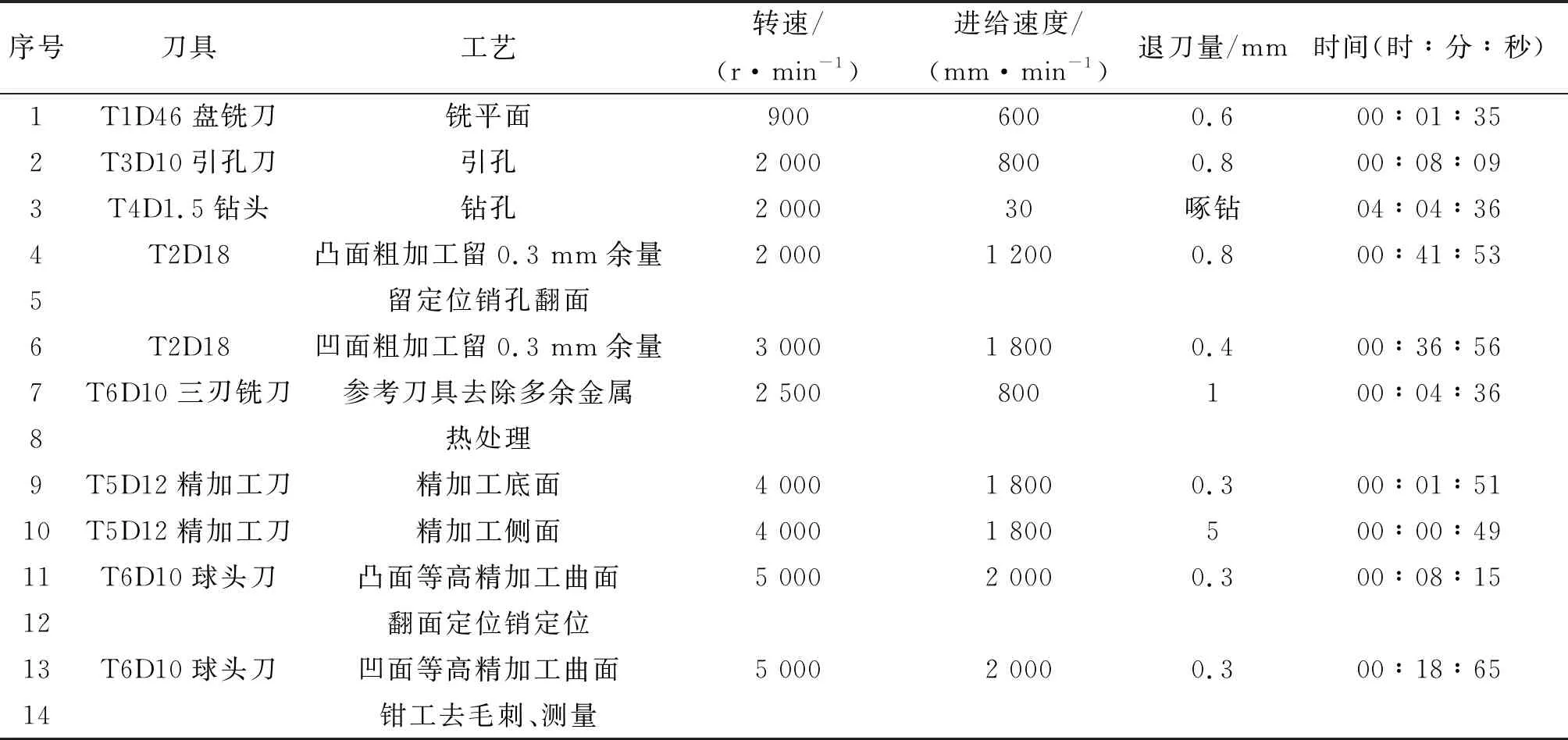
表1 加工工艺清单

精度和刀具的关系[3]如公式(1)所示：

(1)

式中:Rz(h)为理论表面粗糙度(μm)；f为进给量(mm/r)；R为刀尖角半径(mm)。

将上述公式进行移项平方后得到公式(2)：

(2)

整理上述公式并结合铣削加工中表面粗糙度的理论值计算标准式可以得到公式(3)：

(3)

其中理论表面粗糙度Rz和表面粗糙度Ra之间的关系如公式(4)所示:

(4)

进给量f的计算关系如公式(5)所示：

(5)

式中：F为进给速度(mm/min)；n为主轴转速(r/min)。

根据公式(3)—(5)得到公式(6)：

(6)

根据上述结果求得F/n为0.015，所以选择F=30 mm/min、n=2 000 r/min的理论参数较为合理。通过UGCAM软件计算可知，当机床倍率为100%时，按照上述参数加工，完成钻孔程序需要4 h 4 min 36 s。

剩余的特征其加工工艺如表1所示，完成打孔后就可以使用两刃粗加工铣刀进行开粗，留0.3 mm的余量。由于该工件需要热处理，所以要二次装夹，需要先预留好定位销孔，工件“耳朵”上的两个直径5 mm的孔是定位销孔的较好选择。利用D18的铣刀将凹面大部分余量去除，由于凹面在内部，材料很多，如果刀具过大则加工不了，所以还需使用D12的精加工刀具进行二次开粗。完成正反两面的粗加工后需要将工件送至热处理，利用定位销孔再次装夹，使用D10R5的球头刀精加工。

从时间上可以看出，此类零件使用正常的切削参数进行加工很难达到理想结果，所以此次实验的目的是得出切削参数理想值。

3 参数优化

表2所示为孔加工参数。该工件的正常加工方式效率极低，为提高加工效率，只能调整加工参数，使加工时的参数调整到效率很高，所以此次实验旨在找到理想的切削参数。

表2 孔加工参数

3.1 不同切削参数方案

数控批量钻孔加工中，切削速度、进给速度、退刀量3个工艺参数以及刀具磨损状态，均会影响批量加工总能耗和总时间[4]。为达到更高效率的加工，分别从转速、进给速度和不同品牌材质的刀具入手进行研究。退刀量R′一般取钻头直径的1/2，由于加工钻头细小，如果不排除碎屑很容易堵住，使钻头断开，所以该值应谨慎调整[5]。

如表3所示，采用含钴高速钢麻花钻和65°钨钢合金钻头在不同参数下进行加工分析优化。根据上述计算出的理论加工值转速2 000 r/min、进给速度30 mm/min以及退刀量0.8 mm为参考进行上下不同范围调整。除此之外转速和进给速度也在一定范围内正相关，转速越快进给速度也可以相应增加，但是必须在钻头能承受的范围内。

表3 不同加工参数清单

按照扩大再具体化的实验分析原则，将转速范围扩大为1 500～5 000 r/min，进给速度范围扩大到0～80 mm/min，进行实际加工实验，得出不同情况下的结果，再根据具体结果找定区间，缩小具体化的实验[6]。

3.2 加工实验

如图2所示，将加工的3D模型导入软件中。

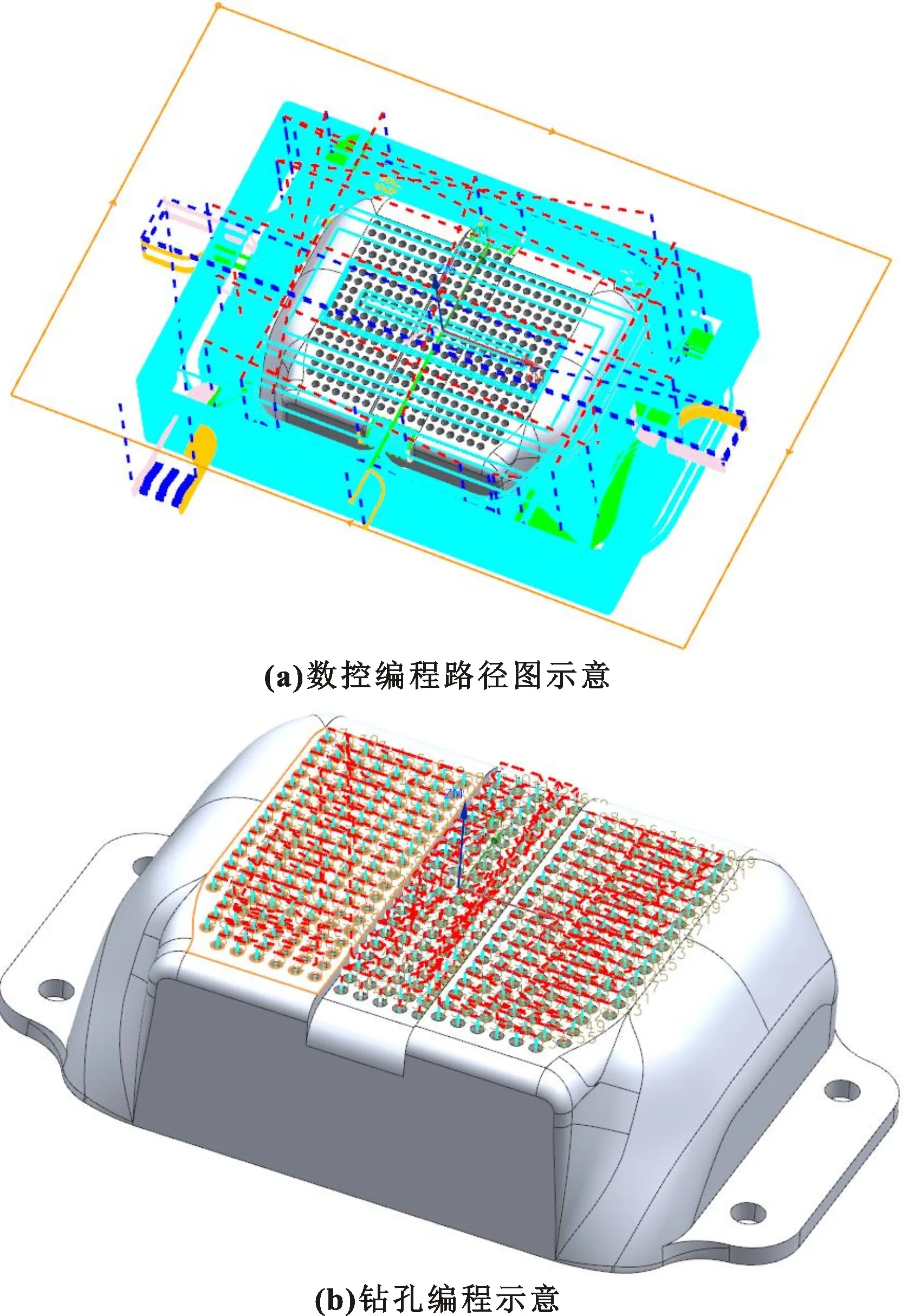
图2 编程示意

操作编程软件插入加工坐标MCS，安全平面为25 mm，指定加工工件，指定毛坯的类型，指定检查避让。根据实际创建刀具、加工工序，得到程序示意图，进行后处理后输出NC代码并上机加工。

完成上述编程后处理设置后，对工件进行装夹并加工，如图3所示。完成后使用分中棒进行分中，用百分表定位跑平，安装对刀。除此之外，批量加工需要专用夹具以提高效率，此次加工使用的是友嘉CM1000-A数控加工中心，其系统是FANUC系统。

图3 加工示意

表4所示为不同加工参数加工结果。可知：所用含钴高速钢在硬度上有所差别，当转速为3 500 r/min、进给速度为50 mm/min时只能勉强坚持一段时间,但是使用65°钨钢合金的钻头则无断刀。所以从实验中大致可以得出：使用钨钢合金钻头，将转速和进给速度分别控制在3 500 r/min 和50 mm/min 左右是可以加工的，但是从刀具表面也看出该刀具的磨损非常严重。

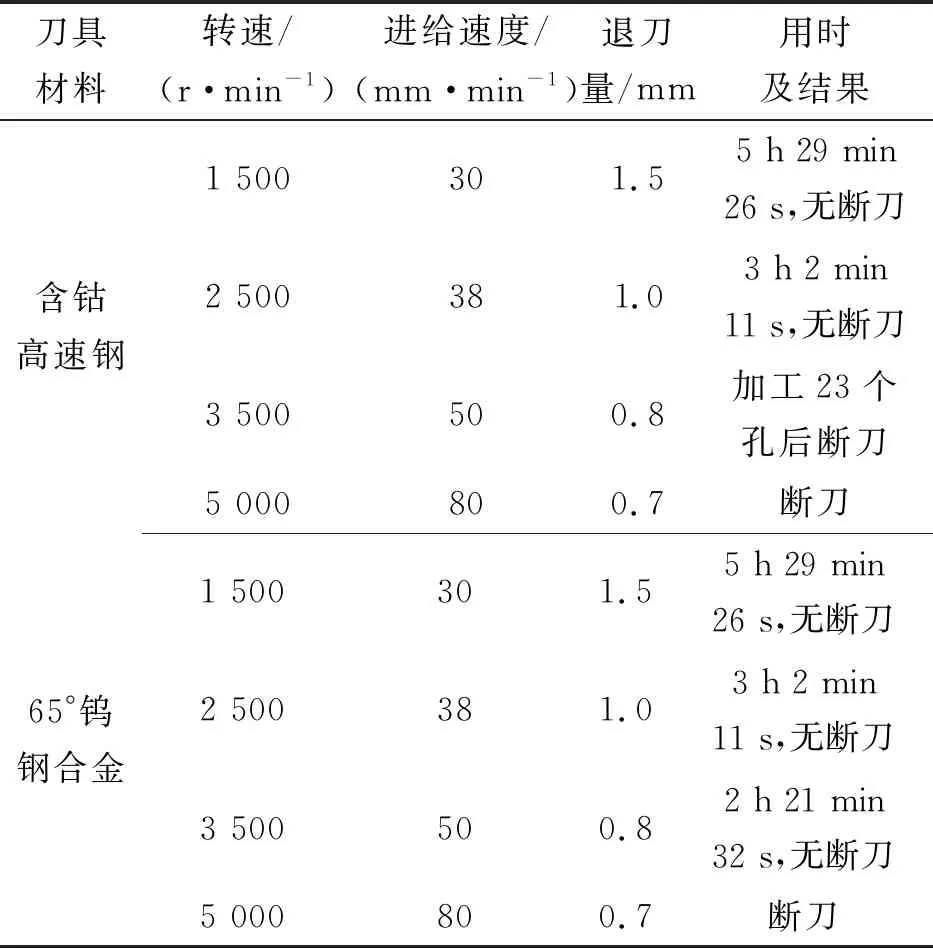
表4 不同加工参数加工结果

将实验结果绘制成双行折线图，用于表示转速和进给速度两个数据在不同阶段对应的磨损值，具体如图4所示，磨损值分为1—10个等级，在转速1 300 r/min、进给速度0 mm/min至转速2 830 r/min、进给速度58 mm/min之间都是可以加工的。但是当到达转速2 200 r/min、进给速度33 mm/min时，钻头的磨损开始严重，并且随着转速和进给速度的增加不断增加，直到达到2 830 r/min、进给速度58 mm/min后钻头断裂无法再进行切削。为了进一步找到能加工又磨损低的解决方案，还需要做连续钻孔实验。

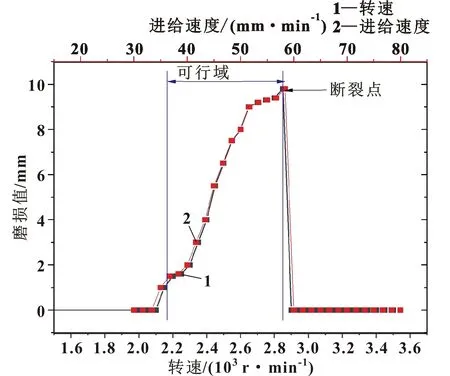
图4 磨损与转速、进给速度区间关系曲线

4 连续钻孔磨损检测实验

如图5所示，该钻头为D1.5合金麻花钻，游标卡尺测量读数为1.49 mm，由于钻孔一般要保证下偏差所以精度合适，长度为6.2 cm，双刃三角面磨制。此次实验用该钻头进行。

图5 实验钻头样式图

如表5所示，按照以上理论，使用该钻头在极限转速3 500 r/min和50 mm/min的进给速度下进行加工。由于单次打孔的次数为367次，都是批量加工，所以在理论效益内刀具最低也要能够完成10次相同的加工，所以取值为367～3 670次的要求。如果效果不满意将再次降低转速和进给速度，不断实验，通过观测其磨损情况找到切削参数的最佳值。

表5 钻孔磨损实验技术参数

如图6所示，随着孔的加工数量不断增加，钻头磨损也明显增加。从图6(a)可以看出：该钻头轮廓明显可见，从凹槽中可以明显看出加工钻头时的磨削痕迹，整体钻头光滑，切削刃锋利完整，无卷曲、倒钝。但是从图6(b)可以看出：钻头的表面镀层已经部分因加工丢失，但切削刃完整且锋利，不影响继续加工。从图6(c)可以看出：该钻头除表面已经磨损严重，主切削刃因取出不及时已经倒钝且丢失，副切削刃被磨损殆尽，不能进行切割且随时有断裂的可能。最后从图6(d)可以看出：由于切削刃磨损严重，不具备切削功能，已经断开。

图6 钻头不同程度磨损示意(显微镜拍摄)

将加工次数和磨损等级绘图，如图7所示：在上述理论切削参数下进行连续小孔的加工实验，0～1 800个小孔连续加工时基本磨损量还很小；当到达2 000个以后基本磨损开始加剧，如果继续加工到2 800个钻头的切削刃口将会消失，此时加工的小孔已经不合格，如果继续加工钻头将会有扭断风险，造成钻头断裂在工件中。该数据将被使用在数据公式拟合中。

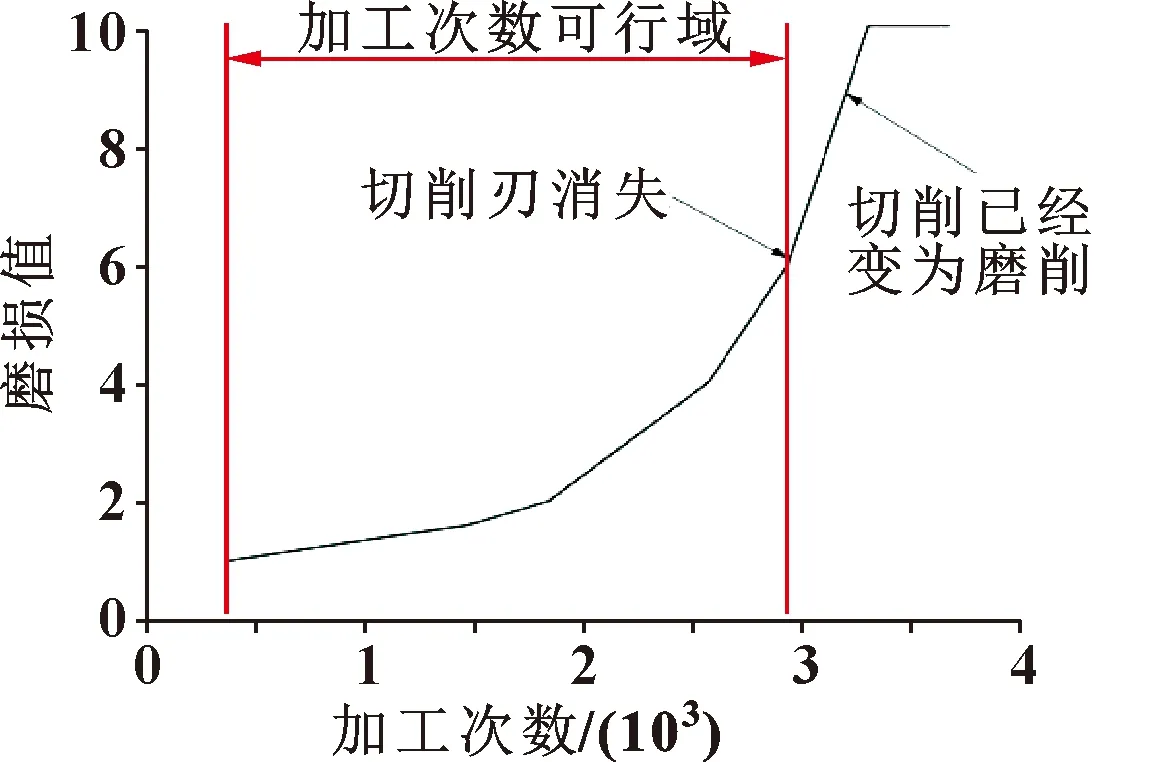
图7 钻头不同程度磨损示意

5 实验数据公式拟合

通过上述实验已知在不同的切削参数下加工小孔得到的不同情况，以及极限加工数量。为了让该数据能够为数控技师在加工此类产品时提供一定的参考，本文作者将以上的数据进行分型，得到数学模型，从而实现灵活、可变的参考作用。

5.1 实验方案

通过数据拟合对多组实验结果进行建模，可以得到转速S、进给速度F、退刀量R′的建议区间，最后得到建议的切削参数。由于数据量过于庞大，所以选择使用数据分析软件SPSS进行辅助分析。

由于切削过程中参数的关系是非线性的，将数据中加工失败即刀具断裂的数据去除，不作为建模数据。因为切削参数不同，影响了最后的加工时间，所以转速S、进给速度F、退刀量R′3个数据作为自变量，加工时间T(min)和最大加工次数作为因变量，搭建非线性回归数学模型。除了上述的变量以外，还要引入abc～jhi作为交叉变量。交叉变量只是作为非线性回归模型搭建时进行多组交叉实验的载体，具体的计算模式如图8所示[7-9]。

图8 非线性回归模型算法

上述模型要能够进行拟合还需要算法的配合，其算法模型如下：

T=a+bS+cF+dR′+eS2+

fF2+g(R′)2+SF+SR′+FR′

(7)

如公式(7)所示，将转速、进给速度、退刀量分别和交叉因子进行组合计算，表明了加工时间、加工次数和转速(S)、进给速度(F)、退刀量(R′)的对应关系，并且求解出abc～jhi的一个估算值。

5.2 SPSS分析

如图9所示，将数据进行整合后，输入上述公式，SPSS软件中修改名称容易造成错乱，故使用原本的参数，即：转速S=V1、进给速度F=V2、退刀量R’=V3。按照公式(7)将数据代入到SPSS中进行非线性拟合，拟合出abc～jhi的估算值。

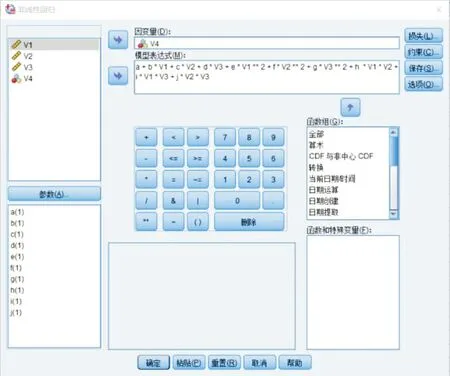
图9 SPSS拟合值

如图10所示：abc～jhi的估计值和实际值之间存在一定的误差，该误差的大小决定了估算值和实际值的相似度。此次拟合建模中其误差值普遍都小于1，其中b和h的误差虽然一个为26.496，一个为2.944，但是相对于估算值41 108.578和4 567.582来看，占比依然是很小的，也证明此次计算出来的数值接近真实值。

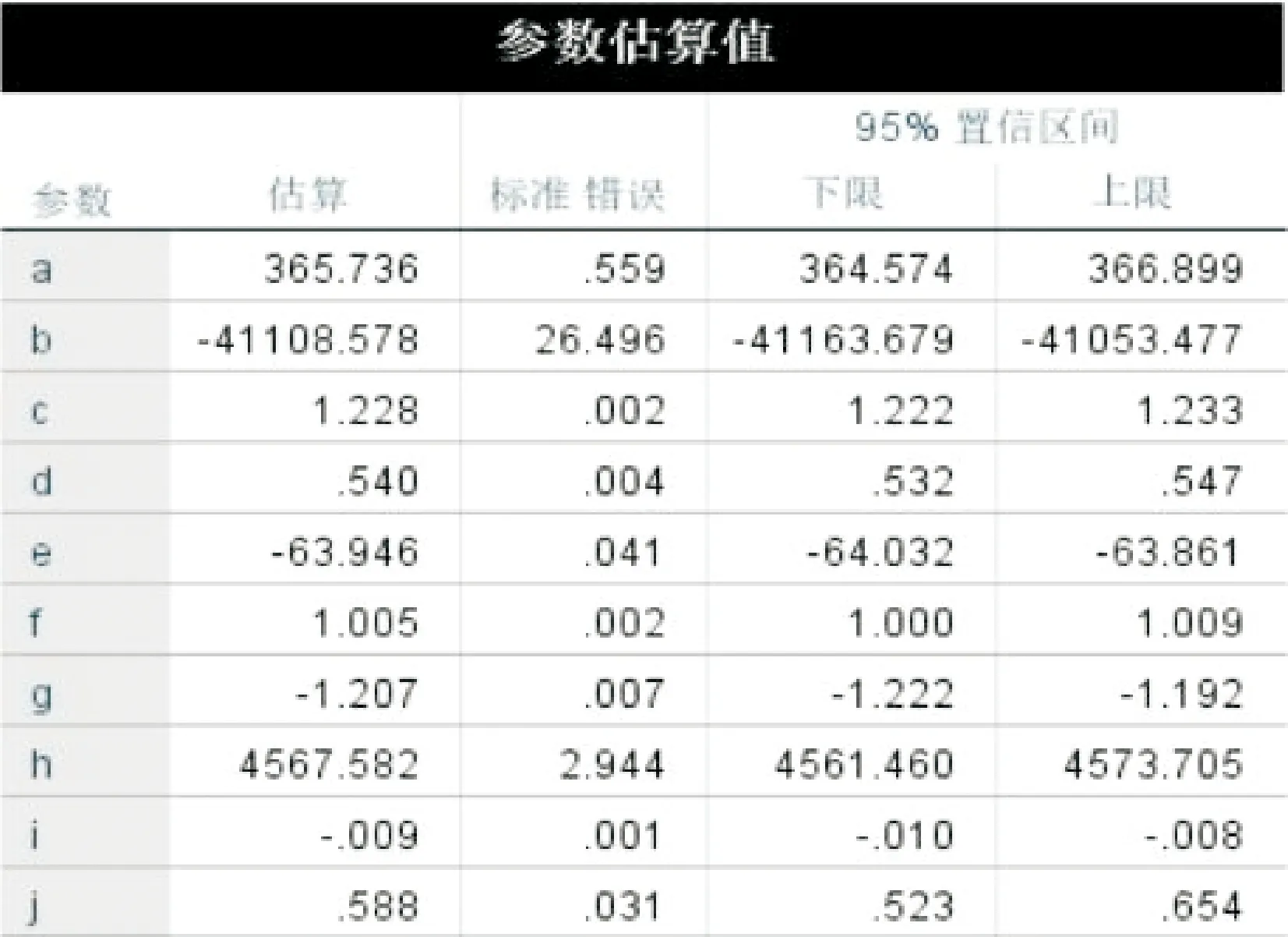
图10 SPSS估算值

综上已经通过建模计算出来了abc～jhi的估计值，并且该值很接近真实值，所以可以根据该值联立三元一次方程组求解出转速(S)、进给速度(F)、退刀量(R′)的最大值、最小值、最优值。

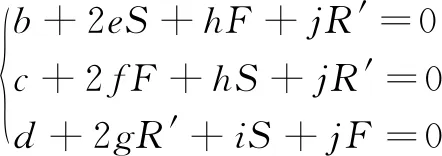
(8)

也就是说通过以上的拟合后，在多组数据中得到了理想的切削参数区间。

5.3 切削参数求解

通过以上的参数求解，可以手动联立方程求解，也可以利用软件中的规划求解进行解算。软件解算的过程如图11所示，可以对目标值进行解算，求出最大值、最小值、目标值(理想值)[10-11]。

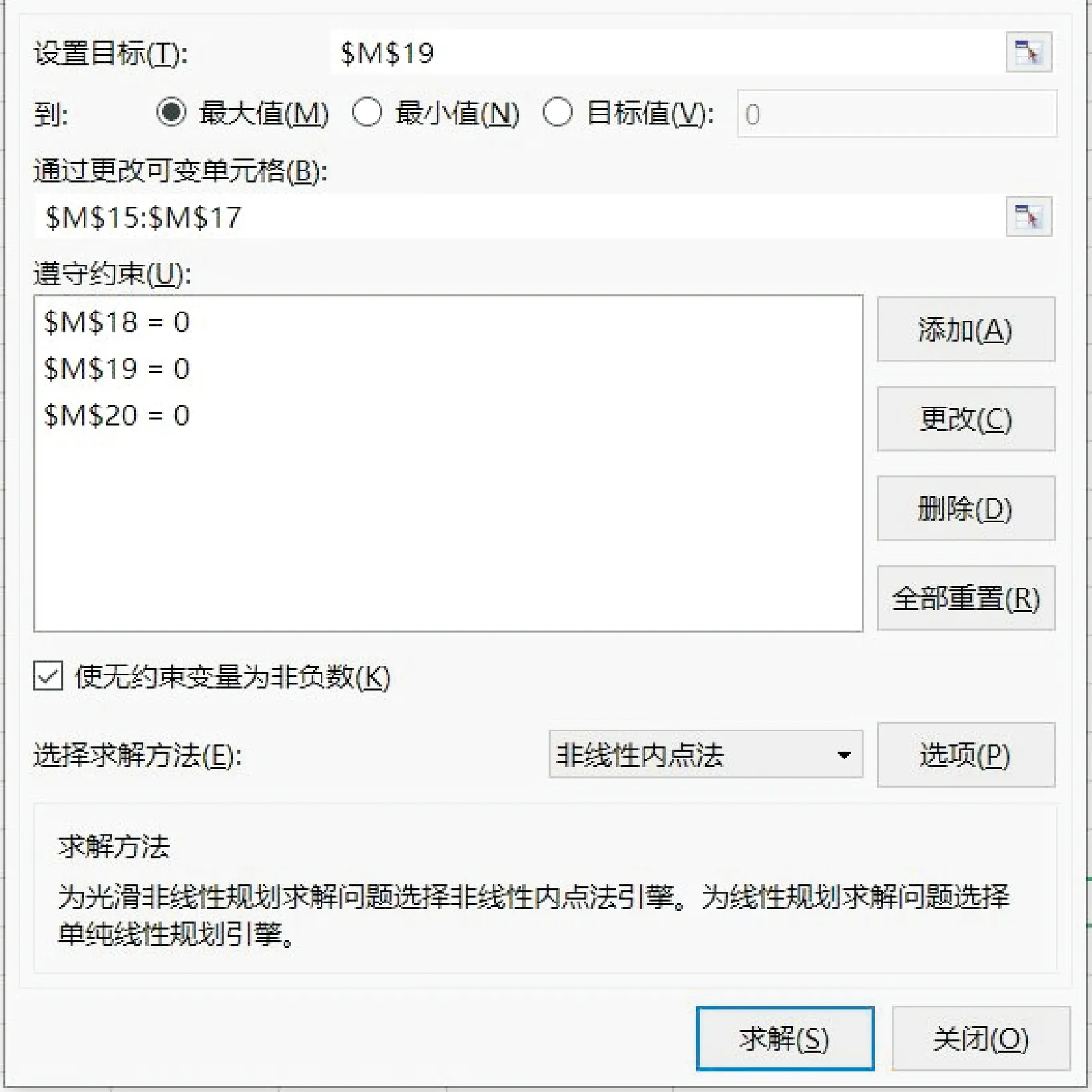
图11 规划求解

求解结果如表6所示，可以看出：转速最大值为3 215 r/min，最小值为2 872 r/min，理想值为3 015 r/min；进给速度最大值为48 mm/min，最小值为32 mm/min，理想值为41 mm/min。单次退刀量由于钻头本身比较细，排屑也不顺畅所以波动并不大，故根据表中结果1.0～1.5 mm，取一个偏小值1.15 mm较为可靠[12-13]。从计算结果来看比较符合实际加工情况，因此通过多次实验和计算得到的数据能够更好地、更直观地为数控技师提供参考。

表6 非线性回归求解结果

6 实际加工验证

为了验证以上的理论正确，将采用以上数据进行实际的数控加工，验证计算出来的理论数据是否可行，是否能够在规定时间内完成加工。

6.1 程序编制及参数赋值

运用CAM软件对上文中的小孔零件进行加工，由于需要做同类对比，故除了孔加工参数以外，其余的参数皆采用表1中的值，这样可以保证最后的数据可以和之前的数据做同类对比，保证实验公平[14]。除此以外，加工孔时是参数如图12所示，按照计算结果转速设置为3 015 r/min，切削进给速度设置为41 mm/min，每次切削深度为1.15 mm。按照以上参数进行实际加工，论证数据的可行性和可靠性。

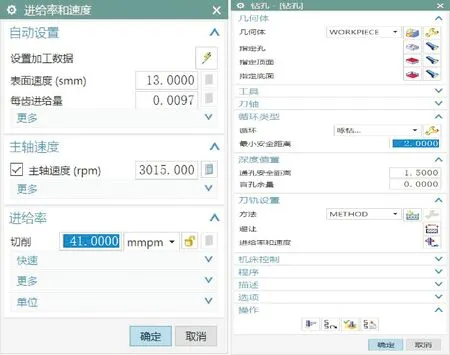
图12 编程参数赋值

6.2 实物加工

按照以上参数在同样情况下进行加工，其加工方式和加工工艺如上所述重复进行，不再赘述。最终实验证明计算得出的数据能够稳定地运行加工。实际加工后的产品如图13所示，能够正常地加工，且中途无任何断刀等情况。

图13 加工实物

但是在实际加工中作者也发现了转速和进给速度还可以做一些经验上的调整，进给速度可以提升到48 mm/min左右，转速也相应地提升至3 500 r/min左右，效率还可以增加8%～14%，但是会带来钻头磨损加快的问题。如果是“急件”加工可以采取此种方式，以牺牲刀具的寿命换来加工时间，当然如果要稳定加工就直接采用表3中的参数较为稳妥。

7 结论

综上所述，公式求出的正常值通过加工实验可行后，将数据范围扩大以寻找合适区间，并且在合适的区间中进行连续加工分析其稳定性；利用上述加工得到的多组结果，将实验中的转速S、进给速度F、退刀量R′和加工结果利用SPSS软件构建了非线性回归模型，引入参数abc～jhi并且解出其理想值；最后联立方程算出了理想的转速S、进给速度F、退刀量R′。本文作者做了大量的实验，为此类产品的加工提供了参考。