UKF算法在七自由度机械臂逆运动学求解的应用

黄宗建， 方涛

(1.河南工业职业技术学院机电工程学院， 河南南阳 473000；2.长春大学机械与车辆工程学院， 吉林长春 130000)

0 前言

六自由度机器人的逆运动学已经相当成熟，然而其较差的避障能力和较弱的操作灵活性限制了其广泛的应用[1]。七自由度机器人是一种众所周知的冗余机器人，它有七个关节来驱动末端执行器，冗余自由度大大提高了系统的避障能力和操作灵活性，然而求解七自由度机器人的逆运动学是非常困难的，因为它们有无穷多个解。

现有文献对七自由度冗余度机器人的逆运动学进行了大量的研究，目前研究逆运动学方法可分为3种类型:几何方法、数值方法、智能算法。几何方法是利用机器人连杆之间的几何关系来获得逆运动学的闭合/解析解[2-4]。对于七自由度机器人，无限的几何关系使解决方案不可能实现，除非指定预定义的“冗余φ”或附加的关节约束。通常，有指定的“冗余φ”，逆运动学的原始映射为(θ1,θ2,…,θ7)=f(x,y,z,α,β,γ)，变成(θ1,θ2,…,θ7)=f(x,y,z,α,β,γ,φ)，然后应用优化算法获得“冗余φ”和联合变量的最优解，几何方法效率高、可靠性高、精度高，但只能应用于具有特殊结构的机器人。数值方法采用数值迭代算法求解逆运动学。常用的数值方法有伪逆-雅可比法[5]、梯度投影法[6]、加权范数法[7-8]等。这些方法简单，通用性强，不需要特殊的结构。然而这些方法需要高性能的计算机硬件，它们有累积误差，对初始值敏感，并且不能保证找到可行的解决方案。智能算法有许多不同的形式[9-11]，如神经网络算法、支持向量机、粒子群优化，这些算法通常用于离线求解逆运动学问题。由于计算量大，不利于实时在线实现，且在逆运动学中没有明显的意义，也不能保证收敛和准确。

在前人研究的基础上，本文作者采用一种新的数值序列处理方法求解七自由度机器人的运动学逆解，该方法可以看作是传统雅可比伪逆方法在运动学逆问题上的改进，具有数值方法简单、通用性强、计算效率和可靠性高、不需要特殊结构等优点。为了验证该方法的有效性，对所提方法进行了仿真，并与传统的雅可比伪逆方法进行了比较，分析了两者的差异。最后在真实的机器人系统中测试了所提方法的有效性。

1 冗余机械手闭环框架算法

1.1 无迹卡尔曼滤波算法

无迹卡尔曼滤波(Unscented Kalman Filter, UKF)算法由于较高的实时精度，在非线性系统估计方面具有广泛的应用。UKF的核心是无迹变换(Unscented Transform，UT)，直接作用于非线性动力学模型过程中，不需要线性化，即不需要计算其雅可比矩阵，可以处理不可导非线性函数[12]。与扩展卡尔曼滤波算法相比，UKF算法具有更好的实时性和更高的精度。因此，UKF算法在系统参数估计领域得到了广泛的应用。利用UKF系统状态估计方法构建自适应最优控制器，能够克服外部复杂性和非线性等因素引起的机器人系统动态参数的不确定性，提高了系统的鲁棒性和机器人定位的准确性。JOUKHADAR 和 KASS HANNA[13]提出了小脑模型关节控制器(Cerebellar Model Articulation Controller，CMAC)算法来估计机器人末端执行器的姿态，并使用UKF算法来比较机器人的实际运动参数和名义运动参数。对串联机器人的运动参数误差进行了自标定，其优点是可以在不停车的情况下对机器人的姿态进行准确的修正，从而提高了动态条件下机器人修正的效率和实用性。可见UKF算法已经成为世界上在线系统建模方法的一个研究热点，并取得了丰硕的研究成果。

1.2 闭环框架

传统的序列驱动模型总是向前移动，没有信息作为反馈来修正其输出，可能会由于估计误差的累积而逐渐偏离真值。这类典型的实例如图1所示。

图1 传统的序列驱动模型

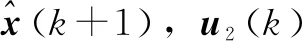
(1)

式(1)中：K为时变增益。为构建状态空间形式的闭环框架，需建立2个模型，如图2所示。在闭环模型中，可以使用UKF等滤波算法估计在线状态。

图2 用于多维序列处理的闭环框架模型

在闭环框架下，估计的状态不会偏离它们的实际值，因为测量可以反馈实时的状态估计。此外，当多维向量u(k)中包含冗余信息时，可能会增加计算的复杂度，降低模型的精度，但闭环框架可以充分利用冗余信息，并降低计算的复杂度。可以通过机械手末端执行器的运动轨迹作为输入序列，采用UKF算法对闭环模型的状态进行估计。相比之下，传统的雅可比矩阵的伪逆计算方法得到的结果是发散的，而闭环模型产生的估计误差可以收敛到零。

1.3 冗余机械手逆运动学

(2)

定义联合变量的向量为q=[q1,q2,…,q7]，利用D-H法从机器人的正运动学得到：

rij=fijqi=1,2,3j=1,2,3,4

(3)

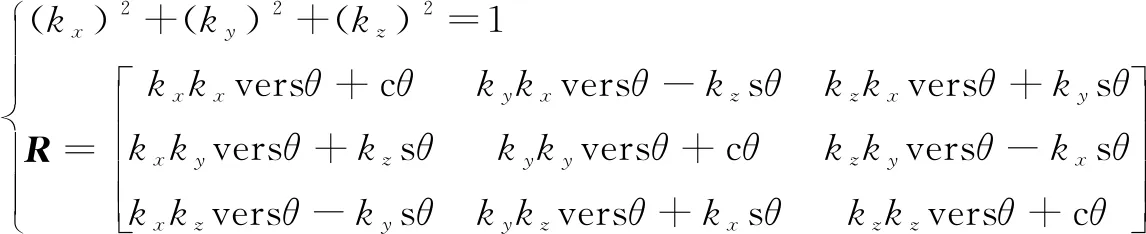
(4)

其中：sθ=sinθ;cθ=cosθ；versθ=1-cθ。式(4)的逆解为

(5)

式(5)表示需要r12、r13、r21、r23、r31、r32来获得旋转轴的单位向量k和角度θ，可将r11、r22、r33视为冗余变量。因此，在逆运动学闭环框架中，末端执行器的齐次矩阵可分为u1=[r12,r13,r21,r23,r31,r32,x,y,z]T和u2=[r11,r22,r33,x,y,z]T。值得注意的是u1和u2有3个相同的变量与位置相关，因为与该位置相关的齐次矩阵中没有冗余信息。

将u1作为输入，将u2视为测量输出，将q视为状态，使用Newton-Raphson方法可以构造状态方程[14]，即闭环框架下的模型A，如式(6)所示：

q(n+1)=q(n)+J+q(n)·[u1(n)-f1q(n)]

(6)

其中：f1(·)=[f12,f13,f21,f23,f31,f32,f14,f24,f34]，J=[∂f1/∂q]为雅可比矩阵，J+为J的伪逆矩阵；n为迭代次数。

采用D-H法对机器人进行正运动学求解，得到闭环框架下的测量方程为模型B，如式(7)所示:

u2(k)=f2[q(k)]

(7)

其中f2(·)=[f11,f22,f33,f14,f24,f34]。结合式(6)和式(7)，即可建立具有闭环框架的七自由度冗余机器人逆运动学的状态空间模型。

2 仿真模拟

分别采用UKF算法和传统的Jacobi伪逆方法对七自由度冗余机器人逆运动学进行了仿真，通过机器人仿真工具箱与MATLAB相结合，在Windows 7操作系统上进行模拟仿真，CPU为Intel(R) Core(TM) i5-3470, CPU为3.20 GHz，内存为8 GB。仿真中使用的七自由度冗余机器人的D-H参数如表1所示，七自由度冗余机器人的关节坐标系如图3所示。

表1 七自由度冗余机器手的D-H参数

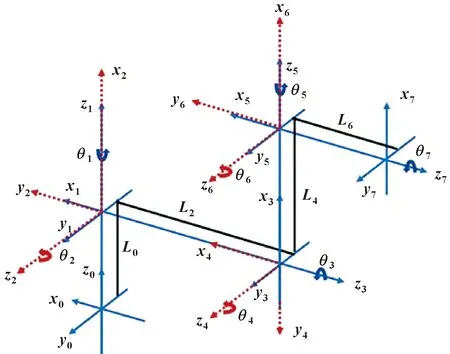
图3 七自由度冗余度机器人关节坐标系

2.1 生成仿真数据

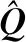
2.2 划分输入序列

为了验证所提出划分输入序列的新方法，进行了2种方案的对比。方案一与参考文献[15]相同，将u分成了u1=[r11,r12,r21,r23,r33]和u2=[r14,r24,r34,r32]；方案二如前所述，将u分为u1=[r12,r13,r21,r23,r31,r32,x,y,z]和u2=[r11,r22,r33,x,y,z]。方案一的仿真结果如图4所示，方案二的仿真结果如图5所示。可以看出：方案一和方案二的所有解决方案都是可行的，方案二的误差是方案一最大值误差的5%，均小于2°，对机器人末端执行器位置和旋转的误差评估有着类似的影响。另外方案二的计算时间短，即计算效率优于方案一，因此新的输入序列划分方法具有一定优势。

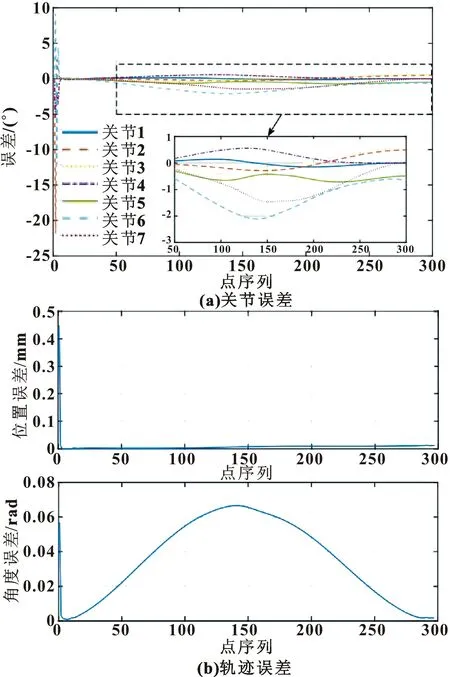
图4 方案一的仿真计算结果

图5 方案二的仿真计算结果

2.3 方法的比较分析

在新的闭环框架中，采用UKF算法作为递推算法进行实时状态的估计。传统的雅可比伪逆方法通常采用基于梯度下降法的迭代算法形式，如式(8)所示：

q(i+1)=q(i)+J+q(i)·{tr2diff[fkineq(i)]t}

(8)

其中，i表示迭代次数，fkineq(·)为正运动学方程，tr2diff(·)将变换差分转换为微分；t为末端执行器的目标齐次矩阵。

传统的雅可比伪逆方法的结果如图6所示，在0.2°以内的误差范围内，传统方法计算的结果，要小于图5中方案二的误差。但轨迹上的3个点(即关节1、关节4和关节7)用传统方法无法求解。因此与传统方法相比，新方法具有更高可靠性。

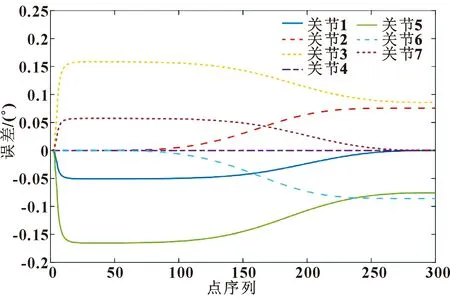
图6 传统的雅可比伪逆方法计算结果

2.4 带噪声轨迹的仿真

在仿真中，将七自由度冗余机器人末端执行器的轨迹输入序列加入高斯噪声，高斯噪声的均值为0，方差为0.001。然后分别采用传统方法和提出的方法对包含高斯噪声的输入序列进行联合变量的估计。估计误差如图7和图8所示，轨迹上的7个点(关节1—关节7)采用传统方法无法求解，由于高斯噪声的影响，传统方法的估计误差是发散的，如图7所示；而新方法的误差即使变大，仍然是收敛的，并且较大的误差低于最大误差。

图7 传统方法对有噪声轨迹的估计误差

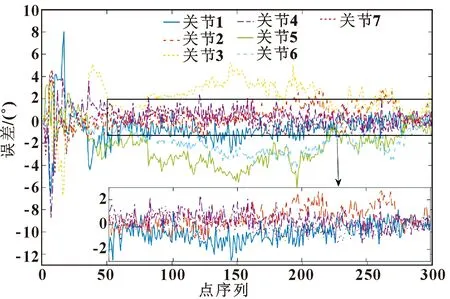
图8 新方法对有噪声轨迹的估计误差

3 实验结果

此实验平台用KUKA KMR iiwa机器人搭建，如图9所示，该机械手具有7个自由度。

图9 KUKA KMR iiwa机器人实验平台

为了验证该方法的有效性，在真实的机器人上运行了该方法。图10所示为基于UKF状态估计的闭环框架计算得到的各关节位置误差，以及正运动学解计算得到的各关节角度误差。通过所提方法得到的机械手终端位置估计误差小于0.07 mm，角度误差小于0.008 rad，该误差可以满足机器人的各种工作条件，即所提方法可以用来求解机器人的逆运动学。

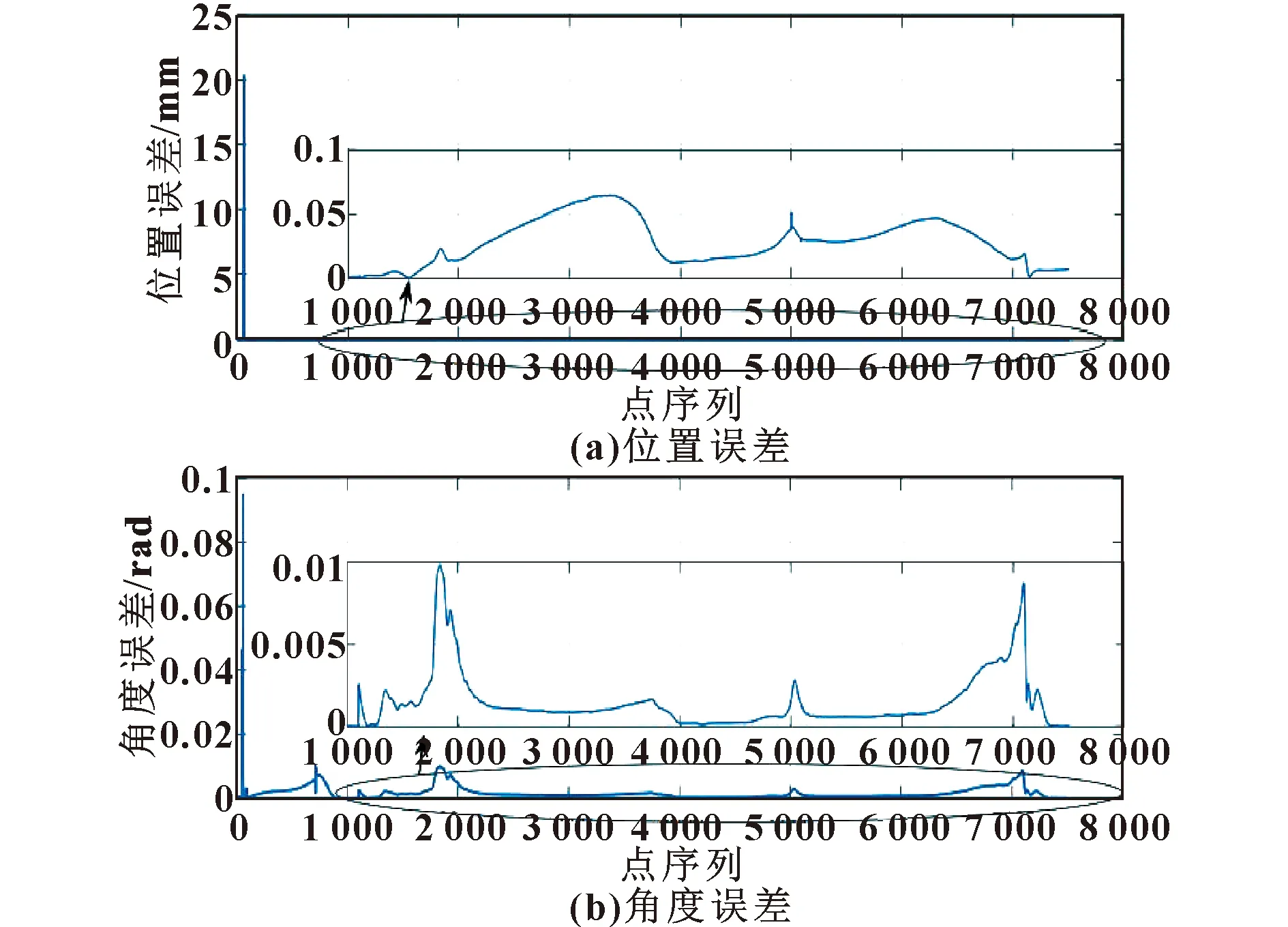
图10 新方法在实验过程中的位置和旋转角度误差

4 结论

在六自由度机器人逆运动学求解的基础上，提出采用一种闭环框架求解七自由度冗余度机器人的运动学逆解。将无迹卡尔曼滤波算法作为递推算法对机械臂实时状态进行估计，提出了在冗余机器人逆运动学条件下划分输入序列的新方法。分析对比了新方法与传统雅可比伪逆计算方法的位置误差精度和计算效率，仿真结果表明新方法计算效率高、可靠性高。当在末端执行器的轨迹中加入噪声时，传统的方法会迅速发散，而新方法的收敛性较好，证明所提方法在七自由度机器人上的应用是可行的，最后通过实验表明该方法具有较高的通用性。