A novel hyperchaotic map with sine chaotification and discrete memristor

Qiankun Sun(孙乾坤), Shaobo He(贺少波), Kehui Sun(孙克辉), and Huihai Wang(王会海)

School of Physics and Electronics,Central South University,Changsha 410083,China

Keywords: discrete memristor,hyperchaotic map,cascade,pseudo-random number generator

1. Introduction

Memristor was proposed by Professor Chua in 1971 according to the completeness of circuit theory.[1]It represents the relationship between charge and magnetic flux.Later, Professor Chua put forward the concept of generalized memristor.[2]However, since it only stayed at the theoretical level at that time,the memristor had not made much progress.Until 2008, HP laboratory firstly reported the real memristor device,[3]which ignited an upsurge of research. Memristor is a nonlinear element with internal state that is completely different from the traditional circuit element,and it can be used to construct circuits with complex chaotic oscillations.[4]Moreover, memristor attracted extensive attention in the scientific community,and was applied in nanotechnology,[5,6]electrical engineering,[7,8]neural network,[9,10]image processing,[11,12]and so on.

It should be noticed that most studies on memristive chaotic systems are limited to the continuous-time domain.[13–17]Comparing with continues memristor, the discrete memristor is more suitable for digital circuits and discrete chaotic maps,which is easily implemented by hardware circuits, and the discrete chaotic maps avoid the disadvantage that the results are difficult to repeat due to the sensitivity of chaos. The design of discrete memristive chaotic maps is a new topic. Heet al.designed an integer-order discrete memristor model and introduced it into several typical chaotic maps.[18,19]Meanwhile,a fractional-order discrete memristor was proposed based on the fractional difference theory and it was added to the Sine function.[20]In 2022, Zhuet al. reviewed the existing memristive elements, including integerorder and fractional-order memristive systems, and analyzed their similarities and differences.[21]Baoet al.reported a new second-order discrete memristive hyperchaotic map.[22]Wanget al. constructed a memristor model and used it to simulate a synaptic connection in a Hopfield neural network.[23]In 2021, Fuet al. established the Simulink model of discrete memristive chaotic map and furtherly verified the feasibility of discrete memristor.[24]In addition,many interesting phenomena, such as coexisting attractors,[25–27]hidden attractors,[28]and multistability,[29]were discovered in memristive chaotic maps and the chaotic maps were used in secure communication successfully.[30,31]

Over the past few years, many people were devoted to the work of enhancing chaos. Huaet al. designed several new chaotic maps by cascading and coupling methods.[32–34]Theoretical verification and experimental results showed that the Lyapunov exponent and chaotic interval were much larger than that of subsystems. Moreover, Huaet al. obtained a high-dimensional Cat map by using a one-dimensional Cat map.[35]Zhenget al. studied chaos by adding a state feedback controller.[36]Yuanet al. designed a cascade memristive chaotic map,[37]but they did not make the internal variables store in the system, and with the increase of cascade times, the total dimension of the generated map did not increase.Inspired by the above discussions,we focus on designing high-dimensional hyperchaotic maps by using the discrete memristor. The rest of this paper is arranged as follows. In Section 2, the quadratic discrete memristor and the memristive chaotic map is presented. In Section 3,the chaotification method and the higher dimensional hyperchaotic map are designed. In Section 4,the dynamical behaviors are analyzed. In Section 5, the NIST test is presented. Finally, we summarize this paper and indicate the future work.

2. The quadratic memristive hyperchaotic map

2.1. The quadratic discrete memristor

According to the definition of continuous-time memristor,the charge controlled memristor is defined by[35]

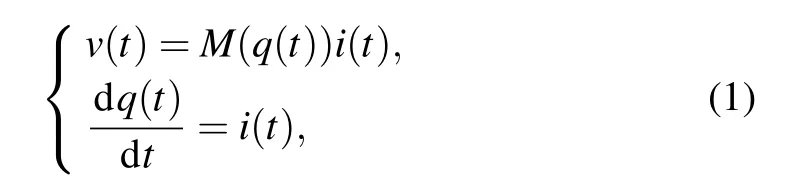
wherev(t) andi(t) are the voltage and the current respectively.M(q(t))represents the resistance function, andq(t)is the amount of charge. The relationship betweenq(t)andi(t)is defined by

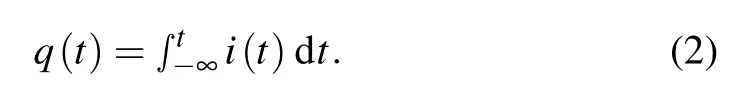
By introducing the difference theory,the discrete memristor is designed as

wherevnandqnrepresent the values ofv(t)andq(t)at then-th iteration,and the equationqn+1=qn+kinis deduced as

Thus, it demonstrates that the current state of the discrete memristor depends on all of the past states. Here, we chooseM(qn) as the quadratic functionq2n −1, and equation (3) becomes to

wherekis the internal control parameter.Here,we setk=0.8.

To verify whether the memristor satisfies the definition of a memristor,we add a sinusoidal voltage signalIn=Asin(ωn)to it. The changes of the voltage and the current sequences are shown in Fig. 1(a). The phase diagrams ofvn–inwith the variation ofA,ω, and the initial valuem0are shown in Figs.1(b),1(c),and 1(d)respectively.It indicates that this discrete memristor meets the three fingerprints of a generalized memristor.[39]

Fig.1. The sequences of vn,in,and the three fingerprints of the memristor: (a)the sequences of vn,in,A=0.01,ω=3,m0=1.3 and the three fingerprints of the memristor when(b)ω =5,m0=0.01,A=0.12,0.2,0.3,and(c)A=0.3,m0=0.01,ω =1,2,3 and(d)ω =1,A=0.1,m0=0.01,2,5.

2.2. The quadratic memristive chaotic map

In the discrete memristor, denoteinas the input for then-th iteration andvnas the output and the next input of the iteration. The quadratic memristive chaotic map (QMCM)[40]is presented as

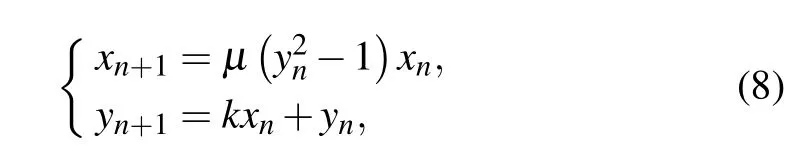
whereµandkare the control parameters.xn+1is the output variable,andyn+1is the internal state variable. The block diagram of QMCM is presented in Fig. 2(a). When the parameters are set asµ= 1.76,k= 0.8 with the initial values (x1,y1)=(−0.5,0.3), the maximum Lyapunov exponent(MLE)is 0.2384,which indicates it is in the chaotic state. The attractor is plotted in Fig.2(b).

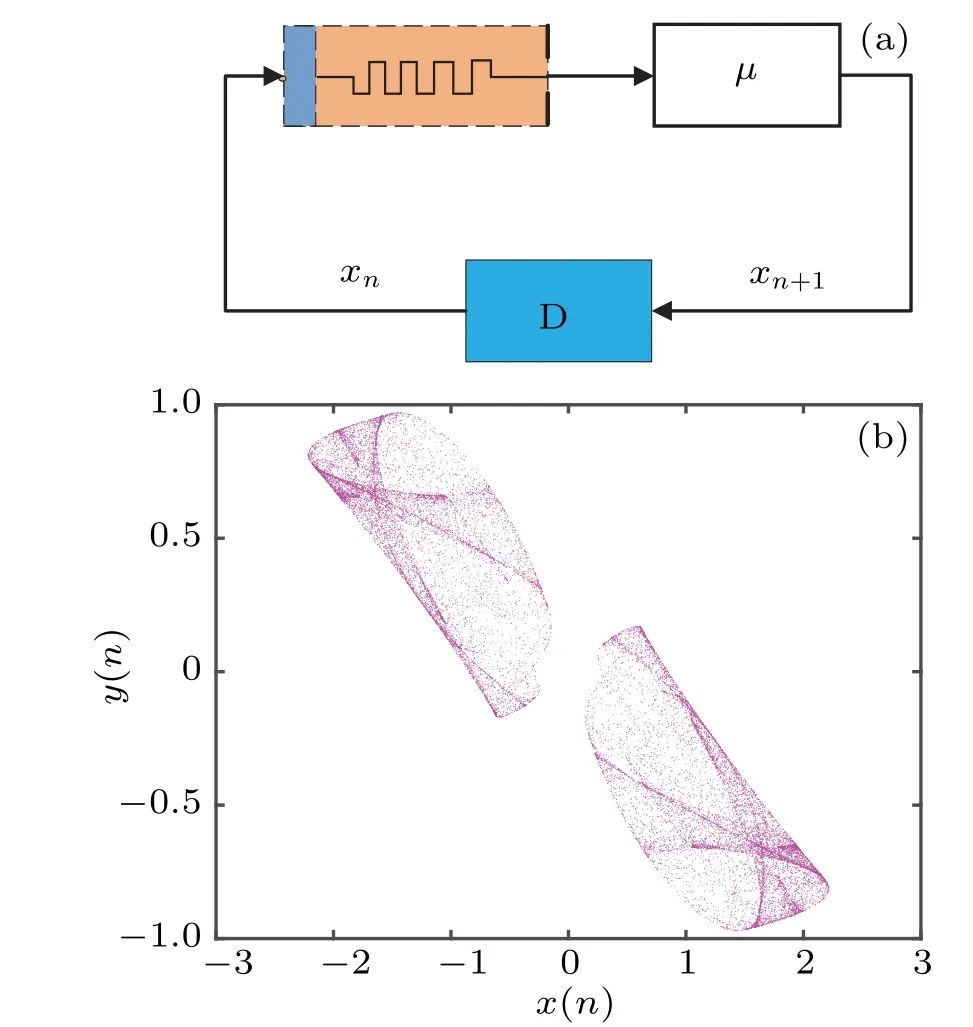
Fig. 2. The block diagram and the attractor of QMCM. (a) The block diagram and(b)the attractor whenµ =1.76,k=0.8.

3. The cascaded memristive hyperchaotic map

3.1. The chaotification methods

Sine chaotification method(SCM)has been proven to be effective in expanding the chaotic range and increasing the chaotic complexity.[34,41]The principle of SCM is to transform the output of a chaotic map with the sine function, and the mathematical equation of SCM is expressed as

whereλis the control parameter.

Cascade chaotification method (CCM) which connects two chaotic maps in series is shown to make the chaotic map be more unpredictable and have larger parameter interval. The output ofG(x)is used as the input ofF(x). The mathematical expression is

Finally,we delay the output of the previous seed mapxn+1to getxn, and then takexnas the input of the next seed map.The state variableyn+1is stored in the memristor. It is worth mentioning that the functions of the resistance can be the same or different to generate different maps.

According to SCM, we takexn+1in Eq. (8) as the input of the sine function,and get the sine-quadratic memristive hyperchaotic map(S-QMHM).Thus,the seed map is expressed as

whereεandµare the external control parameters,andkis the internal control parameter. We set them toµ=1.78,k=0.8,and get the attractors with differentε,which is shown in Fig.3.Whenε= 2.1131, the MLE is−0.2338, and the map exhibits a periodic state. Asε=2.3755, the map has one positive Lyapunov exponent equal to 0.3014, which means it is in the chaotic state, and it is in the hyperchaotic state whenε=2.2801 with two positive Lyapunov exponents.

Fig.3. Different attractors of S-QMHM:(a)ε =2.1131,period;(b)ε =2.3755,chaos;and(c)ε =2.2801,hyperchaos.

The structure of the cascaded S-QMHM is presented in Fig.4. For thei-th iteration,xi(0)is input into DM1,and then goes through the sine function and the delay unit to getxi(1).The obtained sequencexi(1)is used as the input of the second memristor DM2, and then goes through the sine function and the delay unit to getxi(2). In the same way, we finally getxi(m). So far, a complete iteration is completed. In the next iteration,xi(m) will be used as the initial valuexi+1(0). Besides,yi(n)(n=1,2,3,...,m)is stored in each memristor as an internal variable.

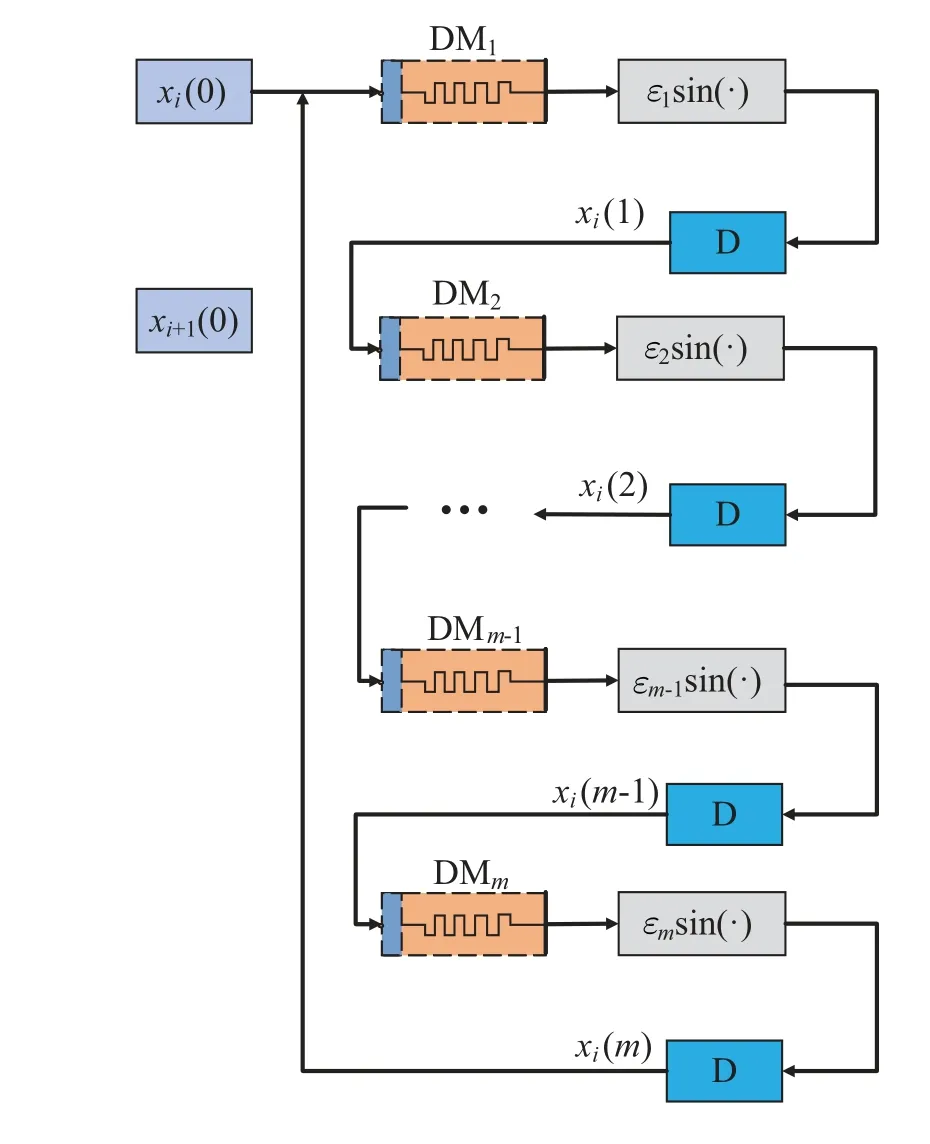
Fig.4. The block diagram of the cascaded S-QMHM.

3.2. The higher dimensional hyperchaotic map

Whenmseed maps are cascaded,the mathematical model is defined by

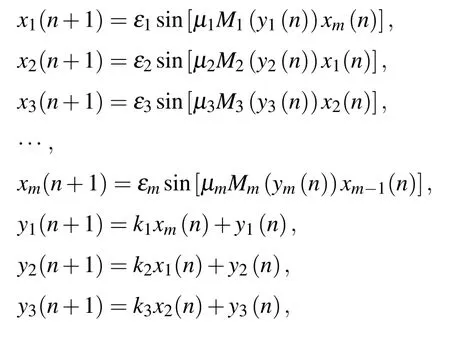
whereε1,ε2, ...,εm,µ1,µ2, ...,µmare the output control parameters,andk1,k2,...,kmare the internal control parameters.Mi(yi(n))depends on the different resistance functions of the memristor.It exhibits that the cascaded chaotic map withmseed maps can produce a 2m-dimensional hyperchaotic map,which shows great potential of building high-dimensional hyperchaotic maps.

4. Dynamics analysis

4.1. Dynamics in the cascaded hyperchaotic map with two seed maps

4.1.1. The system model

Using the chaotification method proposed in Subsection 3.1 and the seed map in Subsection 3.2, we design the cascaded 2-sine-quadratic memristive hyperchaotic map(2-SQMHM) which contains two seed maps. The mathematical model is

and the block diagram is shown in Fig.5.

We set the parameters toε1=1.9,ε2=2.28,µ1=µ2=1.78,k1=k2=0.8,and the initial values(x1(1),x2(1),y1(1),y2(1)) = (0.3,−0.1,0.5,0.2). The number of iterationnis set to 4×105,and the numerical results show that the MLE is 8.8272.The attractor is shown in Fig.6,and it exhibits that the sequence has a wide distribution in three-dimensional space.

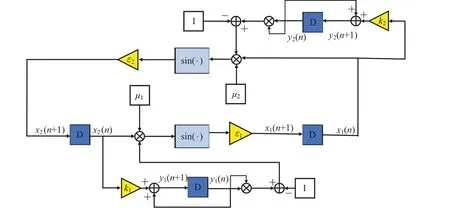
Fig.5. The block diagram of 2-S-QMHM.

Fig.6. The attractor of 2-S-QMHM.

4.1.2. Fixed point analysis

According to the Jacobian matrix and the fixed points expressionF=(0,yi)of 2-S-QMHM(i=1,2,andyiis an arbitrary real constant). The characteristic matrix of 2-S-QMHM is

The eigenvalues are thereby calculated asλ1=1,λ2=1,λ3=(ε1ε2µ1µ2(y12−1)(y22−1))1/2,λ4=−λ3. Therefore,these eigenvalues are related to the parametersε1,ε2,µ1,µ2and the initial statey1andy2. Sinceλ1andλ2always lie on the unit circle,the fixed point is critical stable when the absolute value ofλ3andλ4are not greater than 1. Otherwise,the fixed point is unstable.

4.1.3. Lyapunov exponent and bifurcation

To show the dynamics of the proposed maps clearly, bifurcation diagram and Lyapunov exponents spectra(LEs)are used. We analyze the dynamical behaviors of the seed map and 2-S-QMHM. Noting that all LEs are iterated calculated 4×105times.

When the initial values are set to(x0,y0)=(0.3,0.5)andk=0.8,the LEs and bifurcation diagram of the seed map varying withε,µare shown in Fig.7. It shows that whenε ∈(2.1,2.4) andµ ∈(0.5, 2.5), the map shows chaotic and hyperchaotic behavior. However,the length of the interval is small and there are many periodic windows. In practical applications,the value of the parameters that make the system appear periodic state should be avoided.

Similarly, the initial values of 2-S-QMHM are set to(x1(0), x2(0), y1(0), y2(0)) = (0.3, −0.1,0.5,0.2), andk1=k2=0.8. The LEs and bifurcation diagram varying withε1,µ1are shown in Fig. 8. At the range of (0, 5), there are three positive Lyapunov exponent within most of the interval,and two of them reach around 10. It is worth mentioning that the value of Lyapunov exponents still tends to become larger as the parameter increases. The other positive Lyapunov exponent oscillates around 0.01. Although the value is relatively small,it remains positive. Besides,the number of period window is reduced comparing to the seed map,making the system more stable.

Fig.7. LEs and bifurcation diagram of the seed map. When µ =1.78, (a)LEs versus ε ∈(2.1, 2.4), (b)bifurcation diagram versus ε ∈(2.1, 2.4)and when ε =2.28,(c)LEs versusµ ∈(0.5,2.5),(d)bifurcation diagram versusµ ∈(0.5,2.5).

Fig.8. LEs and bifurcation diagram of 2-S-QMHM.When ε2=2.9,µ1=µ2=1.78,(a)LEs versus ε1 ∈(0,5),(b)bifurcation diagram versus ε1 ∈(0,5)and when ε1=3,ε2=2.28,µ2=1.78,(c)LEs versusµ1 ∈(0,5),(d)bifurcation diagram versusµ1 ∈(0,5).

4.2. Dynamics in the higher-order cases

When 5 seed maps are cascaded,the LEs and bifurcation diagram varying withε1,µ1are shown in Fig.9. Comparing with Fig.8 for 2-S-QMHM,we see that 5-S-QMHM has more positive LEs and a larger hyperchaotic interval.

Table 1. the number of positive LEs and the MLE with cascade times.

As analyzed above, a 2m-dimensional chaotic map is generated by cascadingmseed maps. We set the parameters here to be the same as the seed map. By the simulation experimental research, the cascaded hyperchaotic map hasm+[(m+1)/2] positive LEs ([(m+1)/2] represents the largest integer no more than(m+1)/2). Among these LEs,mexponents oscillate around 10,and the remaining[(m+1)/2]exponents keep positive despite their small values. Table 1 lists the number of positive Lyapunov exponent and the MLE with cascade times. Moreover,in the chaotic interval,changes in the parameters and the initial values do not affect the number of positive Lyapunov exponents.

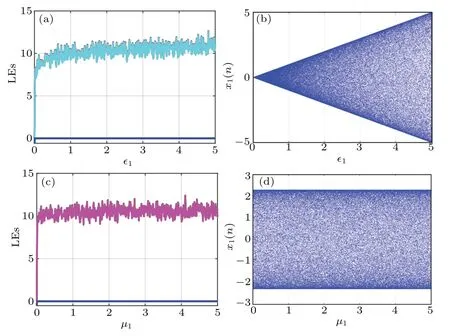
Fig.9. LEs and bifurcation diagram of 5-S-QMHM.(a)LEs versus ε1∈(0,5)and(b)bifurcation diagram versus ε1∈(0, 5)and(c)LEs versus µ1∈(0,5)and(d)bifurcation diagram versusµ1∈(0,5).

4.3. Sample entropy complexity analysis

Complexity is an indicator to measure the proximity of the chaotic sequence to the random sequence. The higher the complexity, the more random the chaotic sequence. We use the sample entropy algorithm to measure the complexity of these chaotic maps due to its high accurate in the statistical assessment of complexity.[42]

Fig. 10. Sample entropy of 2-S-QMHM with ε1, µ1, k1: (a) ε2 =2.9, µ1 =µ2 =1.78, k1 =k2 =0.8, ε1 ∈(0,5); (b) ε1 =3, ε2 =2.28, µ2 =1.78,k1=k2=0.8,µ1 ∈(0,5);and(c)ε1=3,ε2=2.9,µ1=µ2=1.78,k2=0.8,k1 ∈(0,5).

Fig.11. Sample entropy of the seed map,2-S-QMHM,and 3-S-QMHM:(a)the seed map(ε,µ)and(b)2-S-QMHM(ε1,µ1),and(c)3-S-QMHM(ε1,µ1).

In the following experiments, sample entropy of 2-SQMHM is calculatedversus ε,µ, andk. As it is shown in Fig. 10, sample entropy holds a small value in periodic windows and it remains greater than 2.2 in most range. In addition,the complexity of the seed map,2-S-QMHM,and 3-SQMHM are shown in Fig.11,and it shows that the region with high complexity of the seed map is small. With the increase of cascade times,the high-complexity range gradually expands.

The sample entropy of the seed map, 2-S-QMHM,3-S-QMHM, DM-based H´enon map,[18]DM-based cosine map,[43]and DM-based logistic map[33]are shown in Fig.12.Obviously,3-S-QMHM has larger sample entropy than that of other memristive chaotic maps.

Fig. 12. Sample entropy of seed map(ε), 2-S-QMHM (ε1), 3-S-QMHM(ε1), DM-based H´enon map(a/2+0.5), DM-based cosine map(γ/2), and DM-based logistic map(k/2).

5. Pseudo-random sequence generator

Pseudo-random sequence generator is one of the main applications of chaotic map. It is worth noting that the quantization algorithm is an important factor which affects the operation efficiency. For a chaotic sequencebgenerated by 2-SQMHM, the quantization algorithm we adopt is described as follows:[44]

In this way,a sequence with a length of 8Nis obtained afterniterations. In addition,two different quantization methods are adopted to switch,which increases the complexity and further improves the performance on the basis of little impact on the time efficiency.

As for 2-S-QMHM, we set the parameters toε1= 2,ε2=2.28,µ1=µ2=1.78,k1=k2=0.8,and the initial values(x1(0), x2(0), y1(0), y2(0))=(0.3, −0.1,0.5,0.2),then assess the randomness of the generated chaotic sequences by the NIST test. It includes 15 test indicators,and each indicator has two judgment bases, namely, pass rate andp-value. We set the significant levelα=0.01,and number of test sequence groupβ=100,and the length of each test sequence to 64. If the results meet the following two conditions at the same time,the sequences pass the NIST test.

(i)The pass rate of the test results is all within the confidence interval.

(ii)Thep-value is greater than 0.0001.

In addition, the larger thep-value, the better the random performance. The test results are shown in Table 2. It shows that the sequences pass the NIST test successfully.

Table 2. NIST test result.

6. Conclusion

In this paper,we introduced a discrete memristive chaotic map generated by the combination of a quadratic discrete memristor with the sine function. To increase the complexity,we applied a chaotification method.Numerical analysis shows that the generated map has rich dynamical behaviors including more positive Lyapunov exponents and larger hyperchaotic range. As an application,we used the map cascaded with two seed maps to generate pseudo-random sequences. The NIST test results demonstrated it has good randomness and unpredictability. Next, we will focus on studying fractional-order discrete memristors and their applications.

Acknowledgement

Project supported by the National Natural Science Foundation of China (Grant Nos. 61901530, 62071496, and 62061008).