热力耦合作用下水下井口连接器密封特性*

刘统亮 魏行超 冯 定

(1.中海石油(中国)有限公司海南分公司 海南海口 570300；2.长江大学机械工程学院 湖北荆州 434023)

水下井口连接器是水下油气生产系统的重要组成部分，连接器的上部连接采油树，下部连接井口装置，其密封性能对整个水下生产系统的可靠性和安全性有着直接影响[1]。在海上生产过程中，高温高压油气介质及恶劣的海洋环境作用在水下井口连接器上[2]，连接器各部件易发生不规则的热膨胀。同时，由于不规则的热应力往往伴随着不同的温度场出现，热应力对连接器各部件材料的力学性能的影响往往不容忽视。上述热应力和热膨胀可能会对连接器的密封性能产生影响，严重时还会危及整个水下生产系统的安全。

目前，许多学者针对连接器密封展开了相关研究。KELLY和THEISS[3]从水下密封形式的选型出发，探究了不同密封形式的水下密封机制，为满足不同水下密封要求的密封形式选型提供技术方案。OWENS[4]通过有限元和实验分析对井口连接器和井口头之间的相对刚度展开研究，得出金属密封圈密封接触应力随密封锥面、内部介质压力和接触压力的变化规律。BERNARD和MCCOY[5]对2 067 MPa(30 000 psi)压力下的476 mm(18.75英寸)水下采油树井口系统展开分析，利用仿真软件开展井口疲劳测试。绕松海[6]对采油树密封圈密封机制展开了研究，对其受力和变形进行了推导分析。李志刚等[7]提出了一种适用于水下卡爪式连接器的新型复合内外压密封结构。程子云等[8]以锁块式水下连接器为例，分析了连接器在不同工况下密封圈的密封性能随外部载荷的变化情况，但未考虑温度的影响。曾威等人[9]以密封强度为评价指标，分析密封圈密封性能随预紧力、工作压力和结构参数变化的规律。

上述文献对井口连接器在多种工况下的密封特性展开系列研究，获得了其密封性能的变化规律。但这些研究主要集中在密封圈受预紧力、工质压力的影响和密封圈结构优化等方面，在密封性能分析过程中，少有考虑工质压力和环境温度对密封性能的耦合影响。本文作者在前人研究的基础上，以现场使用的锁块式井口连接器为研究对象，建立了连接器密封的热传导和热力耦合的数学模型，针对某气田实际工况对温度场进行数值仿真。在上述基础上，开展不同工况下热-结构耦合数值模拟分析，得到油气介质压力及温度共同作用下水下井口连接器的密封性能变化，以期为工程应用中的风险预测提供理论参考。

1 水下井口连接器温度场分析

1.1 连接器传热模型建立

由热力学第二定律[10]可知：传热的问题普遍存在于水下井口连接器与内部高温油气、外部低温海水接触的工作过程中。在工程实际中，传热方式一般包括热传导、热辐射和热对流[11]，这几种传热方式同时作用于各个部件，情况十分复杂。其中对流换热系数无法直接得到，热辐射与物体温度具有高度非线性，无法直观计算求解，因此在建立传热模型时需忽略影响较小的传热因素，并对传热方式加以简化[12]。根据传热学原理建立下述3个模型：

(1)锁块与井口头之间海水层传热模型。其中井口头的密封面为锥面，锁块与井口头之间海水层非常薄，通过锯齿在连接器锁紧时进行啮合，定义当量导热系数λe1来描述热传递的整个过程：

(1)

式中：λk2为温度T2下海水导热系数，W/(m·K)；r1、r2分别为井口头外径和锁块内径，m；εs为系统的黑度，取0.8；φ1-2为井口头和锁块表面辐射形状系数，计算过程见文献[13]；C0为黑体辐射系数，取5.67 W/(m2·K4)；T1、T2分别为井口头外表面温度和锁块内表面温度，K。

(2)井口头和密封圈之间海水层传热模型。由于密封圈和井口之间的间隙是密封状态，忽略其对流换热，引入该传热模型的当量导热系数λe2：

(2)

式中:λk4为温度T4下海水导热系数，W/(m·K)；r3、r4分别为密封圈外径和井口头内径，m；φ3-4为密封圈外表面到井口头内表面的形状系数；T3、T4分别为密封圈外表面温度和井口头内表面温度，K。

(3)锁块及井口头外表面的传热模型。水下井口连接器的8瓣锁块周向环绕在井口头周围，其外表面与井口头之间的海水会通过间隙流动，引入复合传热系数：

(3)

式中:hc为空气表面自然对流换热系数，取25 W/(m2·K)；T5、T6分别为锁块外表面温度和海水温度，K；ε为锁块黑度，取0.8。

1.2 连接器传热边界条件

不同温度部件之间接触发生的热传递现象称为传热，其边界条件主要有3类[14-15]。

(1)第一类边界条件

若已知条件为物体边界上的温度值，或温度随时间及位置变化的函数，则其边界条件可表示为

T|Ω=T0;T|Ω=fΩ(x,y,z,t)

(4)

式中:T和T0分别为已知温度和物体温度，K；Ω为物体边界；fΩ(x,y,z,t)为已知的温度函数。

(2)第二类边界条件

若已知条件为物体边界热流密度值，或热流密度随时间及位置变化的函数，则其边界条件可表示为

(5)

式中:qr为已知热流密度，W/m2；gΩ(x,y,z,t)为已知热流密度函数。

(3)第三类边界条件

若已知条件为流经物体的流体换热系数和温度，则其边界条件可表示为

(6)

式中:Tf为流体介质的温度，K；hf为换热系数，W/(m2·K)。

对水下井口连接器进行温度场分析，已知连接器内壁接触介质为油气，外部液体为海水，均为流体，温度值已知；在生产过程中传热和对流换热也同时存在，故不适用于第一类边界条件。同时，因连接器处在复杂海水环境中，其热流密度在任意边上无法直接判断，因此第二类边界条件也不可用。考虑文中研究的东方1-1气田实际温度工况，连接器内部高温油气介质温度为121 ℃，外部海水低温为3 ℃，且内外流体介质换热系数可知，因此满足第3类边界条件。

1.3 连接器密封部位热力耦合有限元法

假定研究对象为连续介质时，对体积V进行积分，其边界为S，ρ代表密度。根据能量守恒定理，可得：

(7)

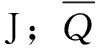
与力平衡方程进行积分化简，引入柯西应力分量σij可得关于热力耦合的能量方程为

(8)

根据文献[16]的推导过程，其有限元方程在结构瞬态温度场与热应力应变场下为

(9)

(10)

式中：Mu、KT、Ku、MT和Cu分别为热力耦合、热学刚度、力学刚度、热学传导和热容矩阵；F、D和Q分别表示载荷、耗散和热载荷矢量。

综合矩阵方程由上述两式合并化简如下：

(11)

式中：P(t)=KTT(t)+Q+D。

接触摩擦生热时表面热流表示两接触面摩擦力的功：

Qfr=MFfrvr

(12)

式中:Ffr为接触面摩擦力；M为功与热转换系数；vr为表面相对滑动速度。

2 水下井口连接器温度场数值模拟

2.1 井口连接器温度场有限元模型建立

基于上述理论分析，建立水下井口连接器的传热模型，对优化后密封结构的温度场进行分析计算。在ANSYS有限元分析过程中，忽略影响较小的因素，并对传热方式加以简化，方便对边界条件的施加。模型主要由树体部分、连接器、井口连接器(内含锁块和驱动装置)和金属密封圈4个部件组成，均为轴对称模型，各组成部件具体如图1所示。局部网格加密如图2所示。密封圈材料为Ni825合金，表1所示为材料属性。

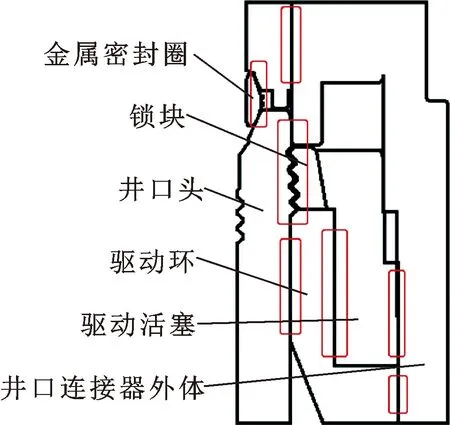
图1 水下井口连接器传热模型

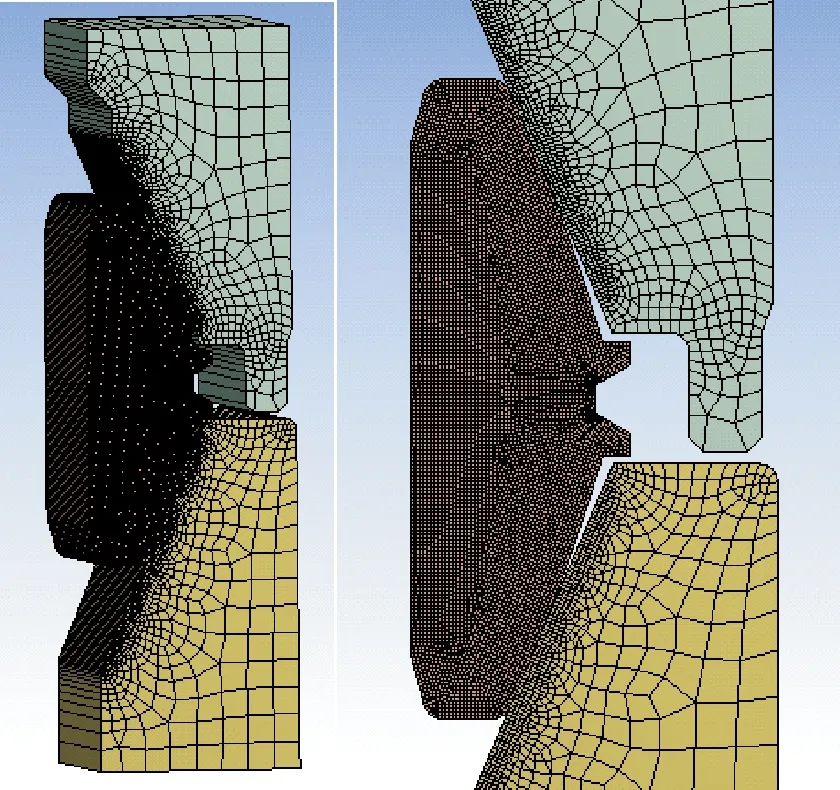
图2 密封圈网格模型

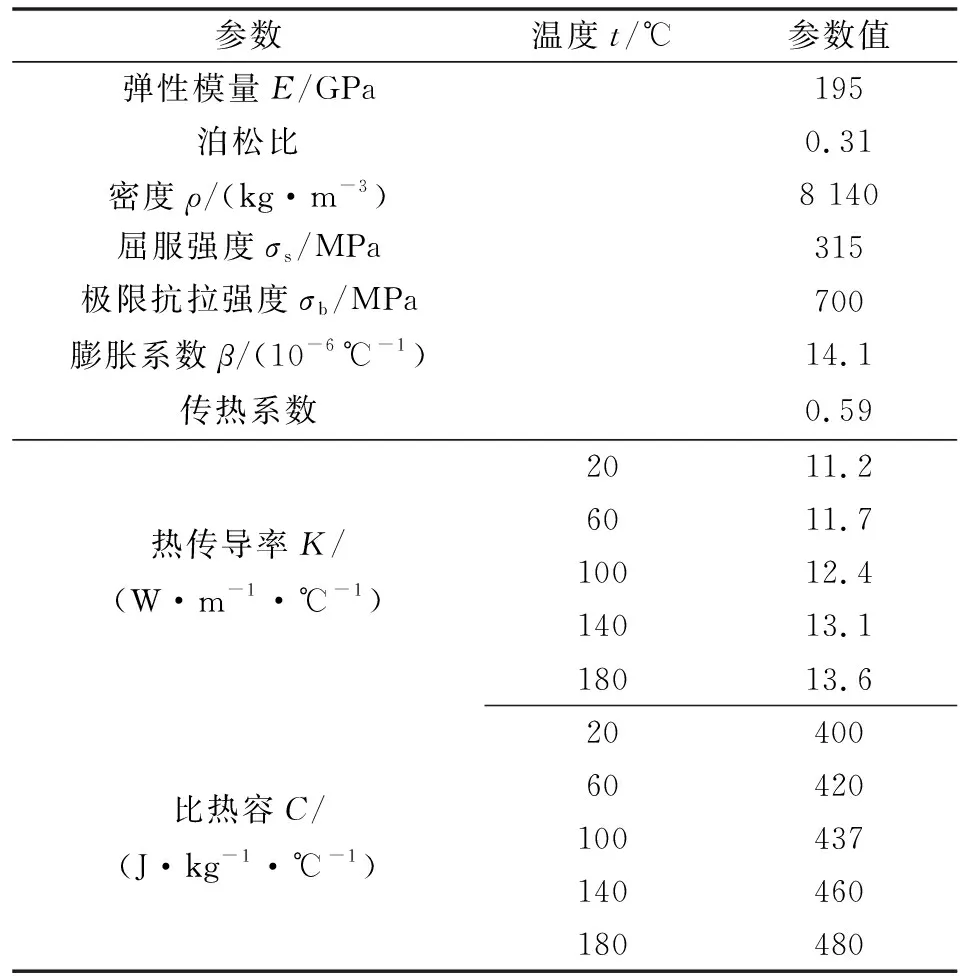
表1 Ni825材料属性

2.2 稳态温度场数值模拟

在正常生产工况下，水下连接器处于额定工作状态，此时稳态温度场数值模拟可很好地反映此时的温度变化。实际高温油气产出液与采油树树体、井口头和金属密封圈的内表面直接接触，流经生产内部通道；而连接器外部暴露在海底低温水中，将温度设置为3 ℃以近似模拟其表面温度。同时根据上文所述第三类边界条件，使用表1中材料的导热系数、热膨胀系数、比热容和传热系数。其有限元仿真模型在传热模型的基础上，除了添加轴向预紧力、介质压力等载荷，还需设置采油树树体、井口头和金属密封圈与生产介质直接接触边界的温度。

为研究水下井口不同温度下井口连接器及密封圈上的温度分布规律，考虑东方1-1气田实际温度工况-18～121 ℃，取油气介质温度分别为-18、10、40、70、100、121 ℃进行研究。此时只考虑外部低温海水和井口内部高温产出液较大温差对井口结构的影响，忽略井口的受力情况。井口头与采油树树体部件传热有限元计算结果如图3所示。

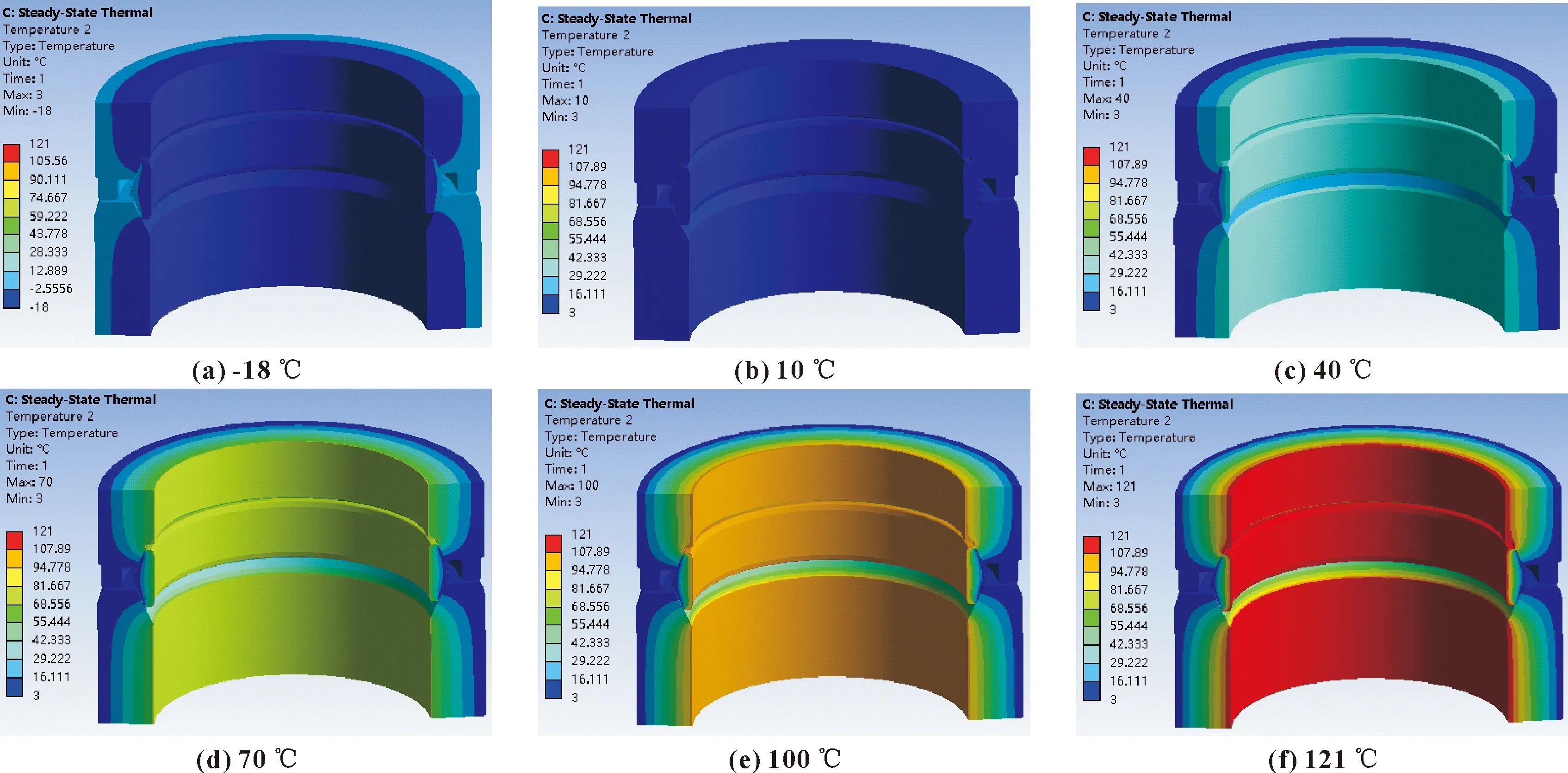
图3 不同油气温度下密封核心部件的稳态温度场云图

高温油气产出液与采油树树体、水下井口头和密封圈的内表面直接接触，周边的井口连接器内外部部件刚下放至海底时，接触低温的海水，密封件的工况较为特殊。由图3可知，随着井口产出液温度升高，密封件内温度梯度也随之增大，且整体温度从内到外依次递减。该仿真结果与文献[13]的密封性能温度循环试验的变化规律一致。因此，有必要分析巨大的温差对密封件内部结构产生的影响。取油气温度最高温度121 ℃，对密封圈的温度场进行有限元分析，结果如图4所示。

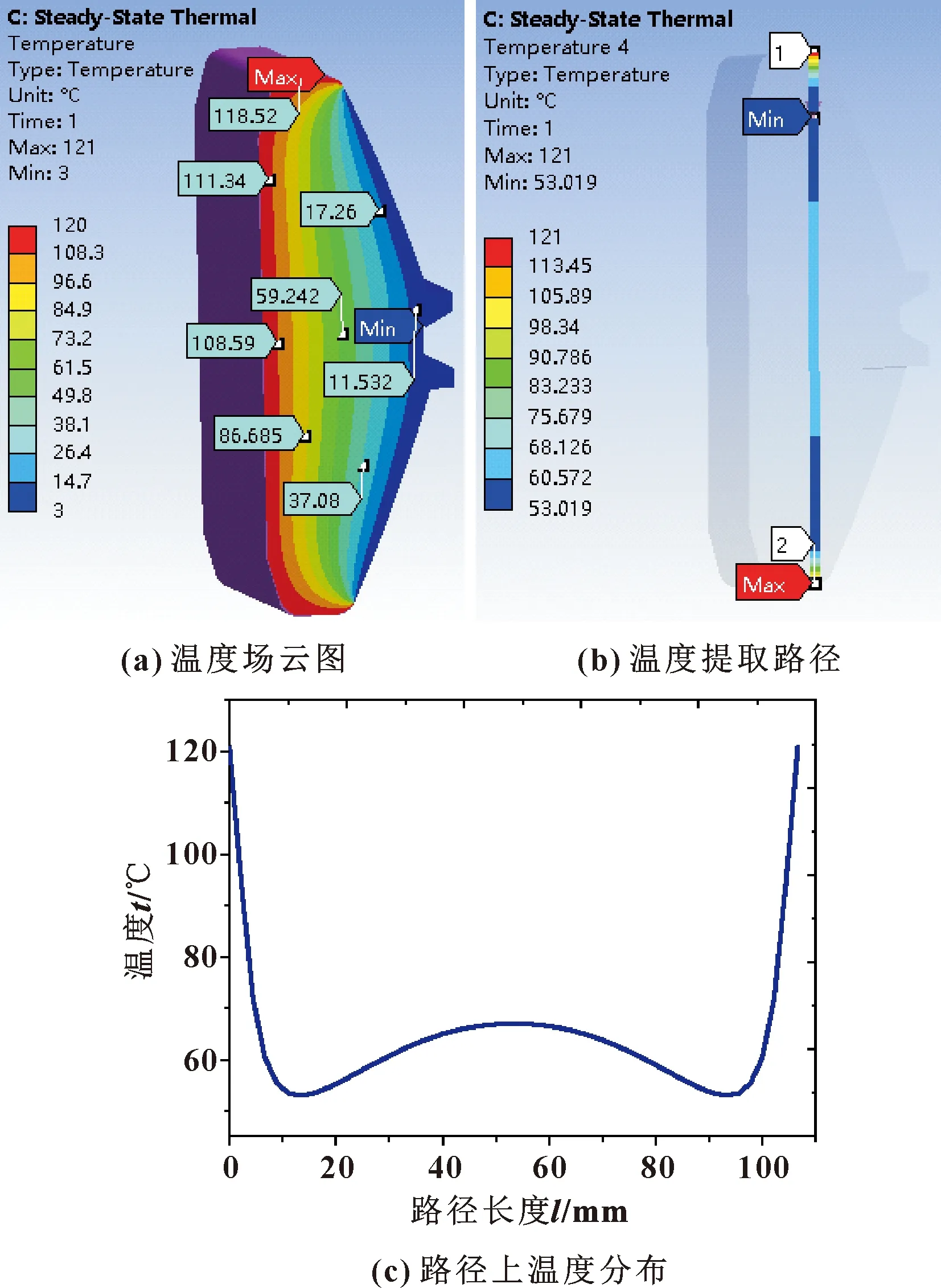
图4 121 ℃时密封圈稳态温度场模拟结果

图4(a)所示为金属密封圈的稳态温度场分布云图。可知，密封圈温度沿周向均匀分布，温度由内至外逐渐降低。建立如图4(b)所示的上端面至下端面路径并提取路径上的温度值，如图4(c)所示。由图4(c)可知，在0～13.335 mm范围，温度由121 ℃快速降低至53.01 ℃；在13.335～53.34 mm范围，温度缓慢上升至67.04 ℃；在53.34～93.35 mm范围，温度再次缓慢下降至53.01 ℃；在93.35 mm之后，温度快速上升至121 ℃。计算结果表明，在稳态温度分布下，该金属密封圈密封性能始终良好，与文献[13]试验结果一致。

2.3 瞬态温度场数值模拟

当水下采油树在开井和关井时，内部油气通道的温度变化显著，为研究不同油气瞬时温度对水下井口连接器密封性能的影响，利用瞬态温度场模拟其内部温度变化。水下井口连接器内部温度变化设置如下：0～100 s，由3 ℃升至121 ℃；100～200 s，由121 ℃降低至3 ℃。通过仿真对不同温度冲击作用下的连接器温度分布进行求解，得到内部温度场在瞬间升降温工况云图，如图5所示。

从图5(a)可知，在15 s时的热量主要集中各部件与油气介质接触的内壁，最高温度为21.74 ℃；随着热量逐渐往各部件外壁扩散，在30 s时密封圈最高温度为38.4 ℃，见图5(b)；在60 s时，温度场分布与30 s时相似，最高温度值提高到73.8 ℃，见图5(c)；在200 s时，内壁温度已经降至初始的3 ℃，此时热量主要集中在树体和井口头中部小部分区域，最高温度降低至35.84 ℃，见图5(d)。

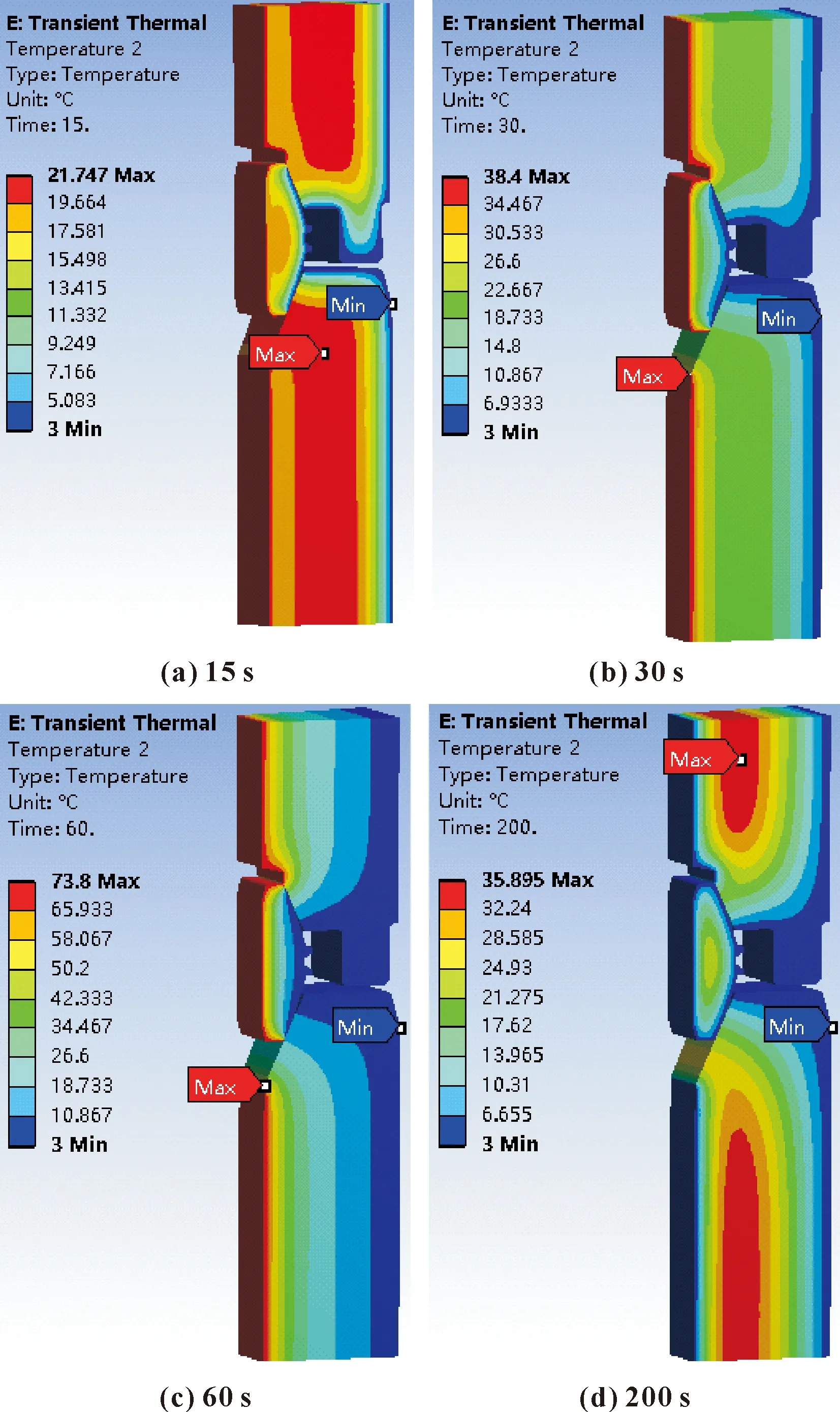
图5 水下井口连接器密封部分瞬态温度场

对100 s时温度参考点的瞬态温度变化情况进行分析，提取密封圈的轴向和径向路径的温度值，如图6、7所示。与密封圈直接相接触的零部件温度变化趋势基本相同，均为温度冲击后出现峰值后下降至海水环境温度3 ℃。同时，密封圈温度最早升至峰值，上部采油树本体和下部井口头则滞后一段时间。由此可知密封圈、上部采油树本体、下部井口头受到温度冲击的作用最大，卡爪和其他部件其次，同时说明温度的冲击波动会对连接器的密封性能产生一定影响。

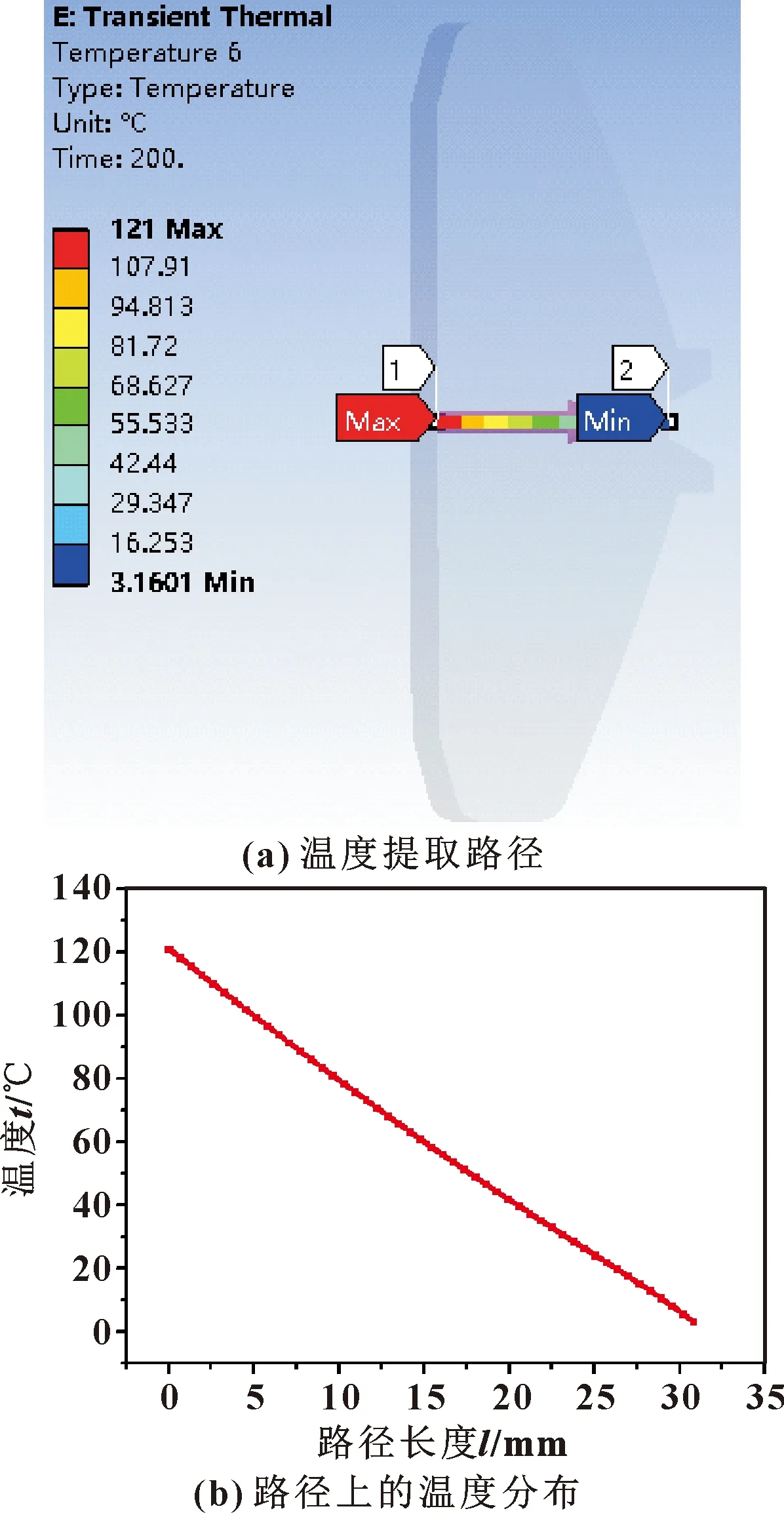
图7 油气温度121 ℃时密封圈瞬态径向温度分布

3 水下井口连接器热-结构耦合密封性能

3.1 耦合应力求解模型

井口连接器的耦合应力场计算，是在传热模型的基础上添加了轴向预紧力、介质压力等载荷，同时设置了采油树树体、井口头和金属密封圈与生产介质直接接触边界的温度，计算仿真复杂。而顺序耦合法可将稳态温度场分析中得到的核心部件各节点温度的“体载荷”直接转化为静态载荷，和其他载荷一同施加在密封核心部件上，得到稳态热-结构耦合应力状态。瞬态热-结构耦合应力求解过程类似。图8所示为稳态和瞬态热-结构有限元求解流程。

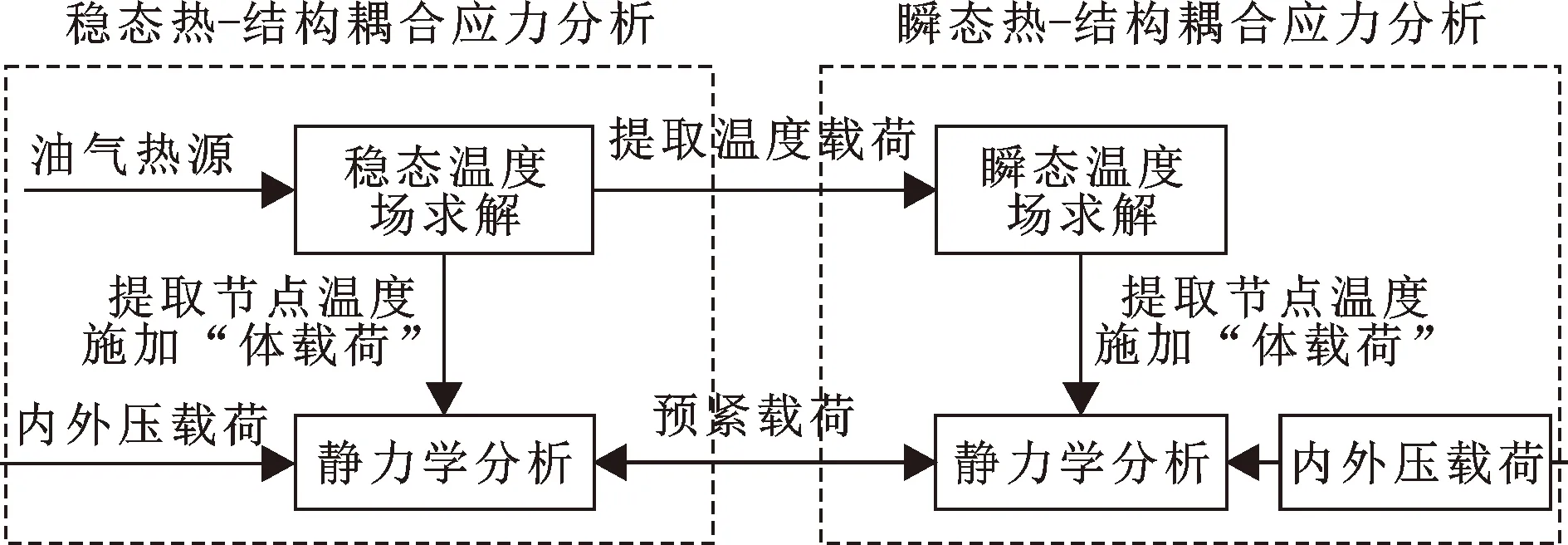
图8 稳态和瞬态热-结构有限元求解

3.2 稳态热-结构耦合数值模拟

为更精确地模拟实际工况，在仿真分析中先进行稳态温度场计算，再将各部件的节点温度作为静态载荷与其他载荷一同施加到井口连接器上。通过前面的分析，除密封核心部件外，连接器其余部件，如锁块、驱动环和驱动活塞等部件等温度变化很小，同时为了简化计算，提高计算效率，文中只对金属密封圈、采油树树体和水下井口核心部件随温度变化进行热-结构耦合数值模拟。在69 MPa高压油气工况下，施加温度载荷前等效应力分布，以及稳态耦合后井口连接器密封圈的等效应力和接触应力分布如图9所示。

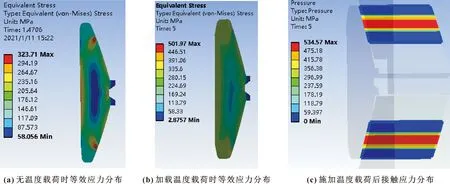
图9 密封圈施加温度载荷前等效应力云图和施加温度载荷后等效应力及接触应力云图

耦合后，密封圈的最大等效应力为501.97 MPa，而无温度载荷时密封圈最大等效应力为323.71 MPa；耦合后密封圈的最大接触应力为534.57 MPa，比无温度载荷时最高应力486.4 MPa高48.17 MPa，由此可知，温度因素对密封圈性能会产生一定影响。

图10所示为无温度场模型和稳态热-结构耦合模型计算的密封圈x、y方向的形变云图，其形变分布规律与文献[13]的仿真计算结果基本一致。对比可知，耦合模型的密封圈x方向最大变形量为0.121 85 mm，位于密封圈中部，与无温度场模型相比变形量增加0.115 088 7 mm。分析上述数据可知，膨胀现象发生在金属密封圈的升温过程中，但由于上下端的采油树和井口头的约束，上下密封接触面分别与采油树下端和井口头上端进行了压紧。

图10 密封圈x、y方向的形变云图

3.3 瞬态热-结构耦合数值模拟

在瞬态热-结构耦合场分析的过程中，在整个模型上选取25、100和200 s的参考点，以便于准确反映井口连接器在瞬态温度场下内部升温变化。仿真计算得到的各参考点温度随时间的变化情况如图11所示。

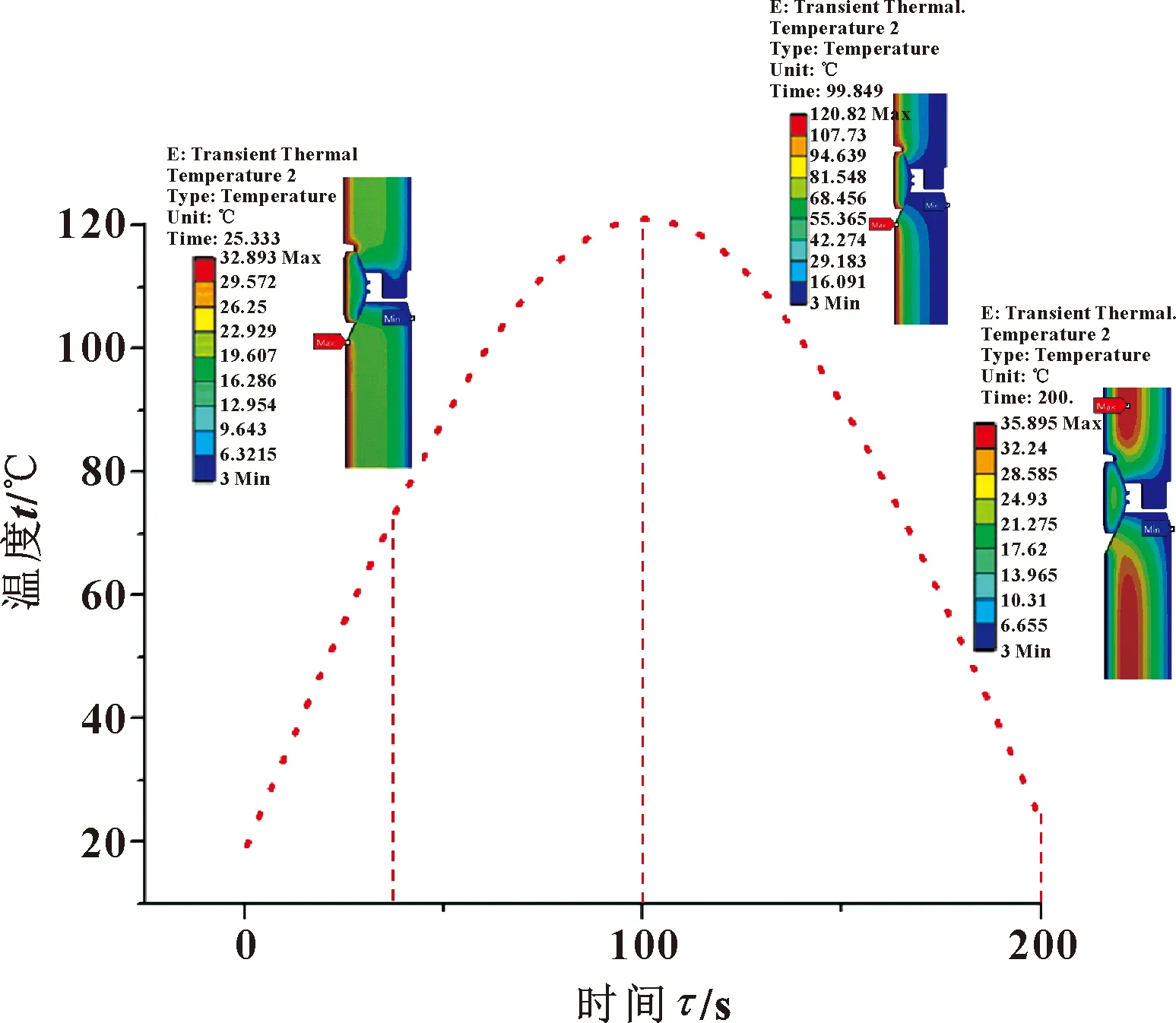
图11 各参考点温度随时间关系图

由图11可知，密封圈、采油树树体和水下井口头三者的内壁，由于和油气直接接触，正常开始工作后，内壁温度会急速升高。前25 s整体模型大部分保持为海水温度，直接接触生产流体的内壁温度开始有明显的上升；在25～100 s之间连接器各部件的温度加速提高，100 s时连接器的内外表面出现最大温度梯度，200 s时密封圈接触点处温度约为10 ℃，采油树树体和井口头接触面上的温度大约为13 ℃。

分析计算得到的瞬态耦合时密封圈等效应力和接触应力分布如图12所示。可知，连接器热力耦合后最大等效应力为465.34 MPa，而无温度载荷时等效应力最大值为323.71 MPa，可见温度对整个模型的应力计算影响很大；耦合模型的金属密封圈最大接触应力为701.68 MPa，比无温度载荷模型的最大接触486.4 MPa高215.28 MPa，表明温度对于密封圈的密封接触性能有较大的影响。

图12 瞬态耦合时密封圈等效应力和接触应力云图

时间节点分别为25、100、200 s时的接触宽度和变形瞬态耦合云图如图13所示。

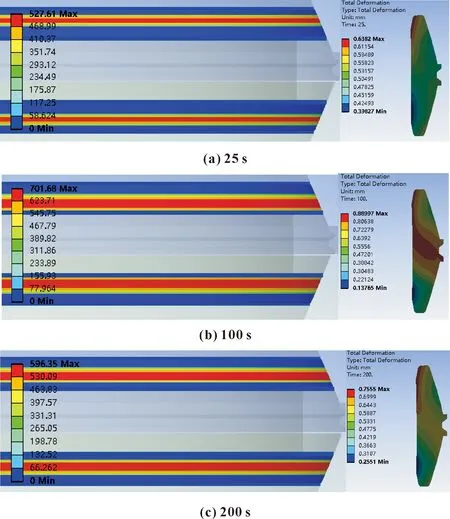
图13 瞬态耦合云图(接触宽度和变形)

由图13可知，在施加温度载荷过程中，由于刚开始升温，与海水接触的连接器一侧温度基本不变，此时密封圈流体侧热膨胀大于密封圈外侧，使其内部发生不协调变形，密封圈进一步被压缩。升温结束后出现的不同密封接触应力峰值相继出现，直至最后连接器内部的温度趋于稳定，热量开始从连接器的内部向外部传递，同时密封圈的形变量也随之减小。

提取整个瞬态过程中最大接触应力数据绘制曲线如图14所示。

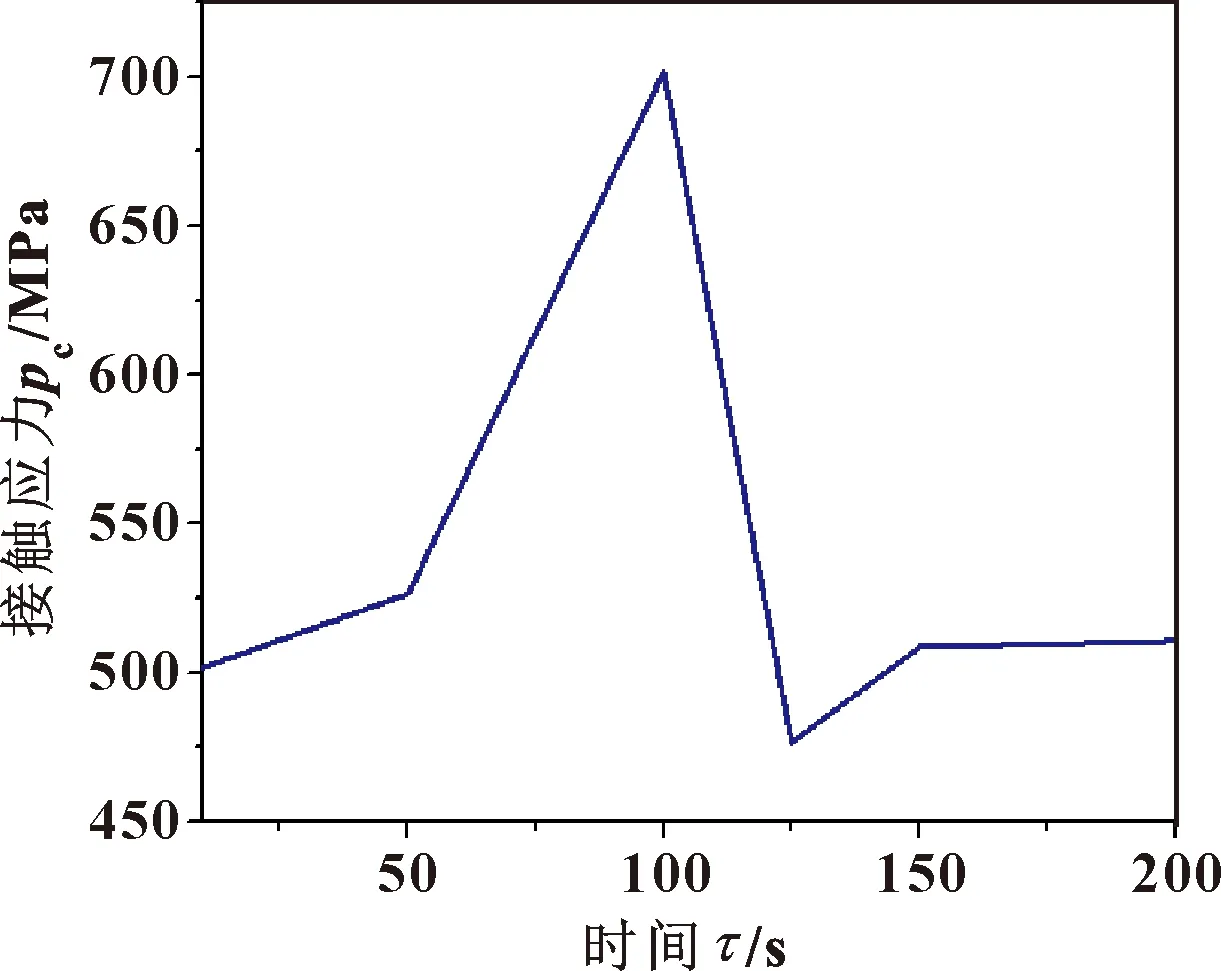
图14 瞬态耦合下接触应力变化

由图14可知，接触压力在0～50 s内缓慢上升，在50～100 s急速增加到最大，在100～125 s又快速下降至最小，随之在125 s后缓慢上升并趋于平稳。在整个过程中，密封接触压力始终满足密封油气要求，采油树树体和水下井口头的最大等效应力最大值小于材料的屈服极限。同时，密封圈的最大等效应力峰值为465.34 MPa，超出其材料屈服强度18%，满足金属密封塑性变形要求。

4 结论

(1)通过有限元软件建立水下井口连接器各部件之间海水层的传热模型，并对连接器密封关键部件的温度场进行了数值模拟，得到了不同井口产出液温度下井口密封部位稳态和瞬态温度场分布。

(2)生产通道内油气介质温度越高，密封件内部的温度梯度越大，连接器各零部件和密封圈之间的温差波动在温度冲击下要大于匀速变温及瞬间变温下产生的温差波动，说明温度变化会对连接器的密封性能产生影响。

(3)稳态热-结构耦合分析表明，金属密封圈会因温度升高而产生膨胀变形，并且该变形大于无温度载荷时的变形，说明温度载荷在特定条件下将对连接器的密封特性产生直接影响。

(4)瞬态热-结构耦合分析表明，井口产出液温度的快速变化导致密封圈中接触面受热产生的线膨胀比靠近海水端外圈中的线膨胀大，从而导致密封圈内部的不协调变形；瞬态耦合过程中的接触应力表明密封圈始终保持较好的密封性能，但由于井口产出液的温度压力频繁冲击，其密封表面易发生磨损和失效，因此在实际工作环境中应避免温度升高速度过快的现象发生。