初中学生数学解题错误的案例研究
⦿广州市玉岩中学 李小兵
《义务教育数学课程标准》明确要求,教师要耐心地引导学生分析错误产生的原因,并鼓励他们自己去改正,从而增强学习数学的兴趣和信心.因此,关注初中学生数学学习中出现的问题,尽可能帮助学生避免或减少解题错误并予以纠正,能够有效地提高初中数学课堂教学质量.
1 知识性错误
知识性错误是指对概念及定理的认识模糊不清或错误运用公式与法则导致的错误;基本技能不熟练,运算基本功不扎实,遗漏或随意添加条件导致的错误;等等.
1.1 概念不清
概念是学生思维的基本形式,也是解题的重要依据.学生在解题过程中由于对概念、规律的内容认识不清或不能正确理解它们的确切含义而产生的一些错误就是概念性错误.
例1下列方程哪些是一元二次方程?
(1)ax2+bx+c=0;
(2)x2=0;
(4)2x2-x-1=0;
(5)3x(x-1)=3x2+1;
(6)(1-m)x2+mx-2=0.
错解:(1),(2),(3),(4),(5),(6).
分析:例1中对一元二次方程概念的理解,特别容易忽视方程ax2+bx+c=0中系数a,b,c的限制条件.授新课时应讲明——(1)a≠0,b,c为常数;(2)三种特殊形式,即ax2=0(a≠0),ax2+bx=0(a≠0,b为常数),ax2+c=0(a≠0,c为常数);(3)方程要先化简为一般形式,牢牢抓住二次项系数a≠0.
1.2 法则不明
初中代数法则多、公式多且易混、易错.学生运算出现问题往往是公式记忆错误,运算法则混淆等.
例2计算:(1)(-4)2=,-22=;(2)(3x-2)2=.
错解:(1)-8 ,4;(2)9x2-4
分析:例2(1)错解的原因是将乘方的运算法则与数的运算法则相混淆了.例2(2)中把乘法公式中完全平方公式和平方差公式记混淆了.
2 逻辑性错误
逻辑性错误主要表现为推理欠严密,条理不清,自相矛盾.有些学生思维发展水平低,推理能力弱,数学知识、能力、方法储备不足,推理思路不明,从而得出不准确的结论[1].
2.1 变形不恒等
把代数式当等式来变形、化简.

错解:原式=2(x-2)-2(x+2)=2x-4-2x-4=-8.
分析:对于例3,学生在进行分式计算时,易将代数式的变形与等式的变形混在一起,错误地将分式转化为整式,从而违背恒等变形这个原则.
2.2 混淆“或”与“且”
“或”表示选择的关系,二者必居其一.“且”表示同时满足.在使用“且”和“或”时不能混为一谈.


x2+4x+3≠0.
整理,得(x+3)(x+1)≠0.

分析:例4中,当x=-3或x=-1时,分母都等于零.要使分式中的分母不等于0,则x既不能等于-3也不能等于-1,两者是一个并列的关系,所以应该用“且”.
2.3 偷换命题
学生在运用三角形中位线定理、等腰三角形三线合一性质、垂径定理解题时,往往将性质或判定的题设和结论混淆,导致论题改变,发生错误.
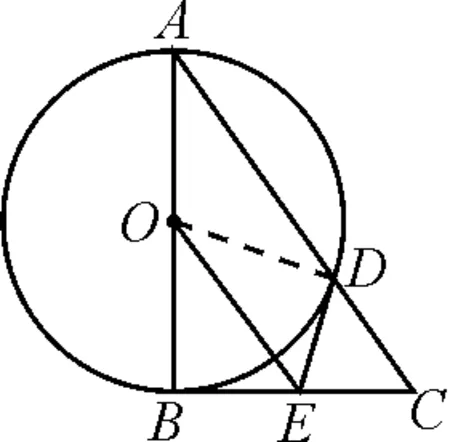
图1
例5如图1,⊙O是Rt△ABC中以直角边AB为直径的圆,⊙O与斜边AC交于点D,过点D作⊙O的切线DE交BC于点E.求证:OE是Rt△ABC的中位线.
错解:连结OD.
∵∠ABC=90°,AB为直径,
∴EB是⊙O的切线.
又∵DE是⊙O的切线,
∴∠BOE=∠DOE.
∴∠BOD=∠BOE+∠DOE=2∠BOE.
又∠BOD=2∠A,
∴∠BOE=∠A.
∴OE∥AD.
∵O是AB的中点,
∴OE是△ABC的中位线.
分析:三角形中位线定理是由E是BC的中点和O是AB的中点得出OE∥AD.例5中由OE∥AD和O是AB的中点得出OE是△ABC的中位线,显然是没有正确认识三角形中位线定理,但可进一步由平行线分线段成比例定理得出E是BC的中点.
3 策略性错误
策略性错误是指考虑不周全导致解题思路受阻或解题方向错误,或选择非最优解法明显增加了解题的难度与出错机会,使得问题最终得不到解决.
3.1 忽视题目中的隐含条件
解题时有些条件隐含于已知条件或图形中,但由于学生马虎大意,未深刻把握数学的严谨性要求,忽视题目中的隐含条件以致得出错误结论.
例6已知关于x的方程x2-2(k-1)x+k2=0有两个实数根x1,x2,且x1+x2=x1x2-1,求k的值.
错解:由题意可得x1+x2=2(k-1),x1x2=k2.
所以-2(k-1)=k2-1.
解得k1=1,k2=-3.
分析:对于含字母系数的一元二次方程或二次函数的问题,学生往往忽略考虑二次项系数不为零、根的判别式Δ≥0等隐含条件,因考虑不周全出错.例6中求k的值要进一步检验根的判别式.
3.2 忽视“分类思想”造成漏解或错解
解题时,如遇到等腰三角形、相似三角形或动点、动直线问题,常常要分类讨论所有可能情况,否则答案不完整.
例7在平面直角坐标系xOy中,点P在x轴上,点A(1,1).若△AOP为等腰三角形,请求出点P的坐标.
错解:满足条件的等腰三角形AOP的点P坐标为(1,0)和(2,0).
分析:应分三种情况讨论.
(1)当AO=AP时,以A为圆心,AO为半径作圆与x轴的交点即为点P,则P(2,0);
(2)当OP=AP时,作OA的垂直平分线,交x轴的于点P,则P(1,0);
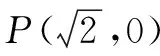
3.3 解题方法繁琐造成错误
同一道题,不同的解题思路或辅助线作法对解题有不同的影响,有的会直接增加题目的计算量和难度,有的会导致思维障碍解不出来.
例8如图2,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.求证:AE=EF.
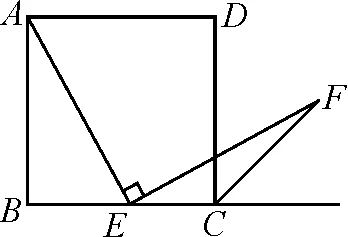
图2
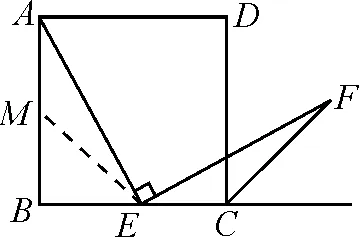
图3
证法1:如图3,取AB的中点M,连结EM.可证△AEM≌△EFC(ASA),从而得AE=EF.
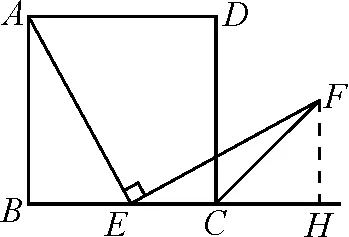
图4

分析:上述两种方法虽然都通过作辅助线利用全等证出线段相等,但显然证法1更简单,证法2在寻找全等的条件时难度更大,实际操作中学生会因缺全等条件而半途而废.
4 心理性错误
心理性错误主要表现为缺乏坚强的意志和信心,导致解题出错的急躁心理现象.良好的心理素质,可以克服心理障碍而减少错误.
4.1 解题思维定式,思维惯性
有些数学题目在形式上相似,在解法上也雷同.学生解题时容易产生惯性思维,“先入为主”匆忙下结论,因负迁移而导致错误.
例9解一元二次方程x(x+2)=3x.
错解:将方程两边除以x,得(x+2)=3.
所以,此方程的解是x=1.
分析:例9中方程两边同时除以x的前提条件是x≠0,而x=0恰好是此方程的一个解.凭经验约分造成漏解.
4.2 思维抑制或情绪焦虑
心理学的研究表明,考试中学生临场过分焦虑,心理压力过大以致于出现暂时性思维障碍,称为思维抑制.考试中,遇到运算数字较大的计算或不熟悉的题型一时找不到思路,就会产生焦虑,有时产生暂时的遗忘,干扰思维的正常运行,导致会而不对,对而不全.
例10已知二次函数y=mx2+(1-2m)x+1-3m与x轴相交于不同的两点A,B.
(1)证明此二次函数的图象一定经过一个定点P,并求出点P的坐标.
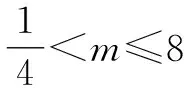
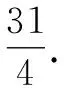
分析:例10证明过定点、求最值问题因不常见往往使学生望而却步,心理上有思维障碍.
4.3 审题马虎、理解肤浅
粗心大意源于不良的学习习惯.审题是解题的关键,许多学生在审题时粗心大意,经常看错题或看漏条件,没能正确地理解题意导致错误的产生.

错解:选A.

德国哲学家黑格尔曾说过:“错误本身乃是达到真理的一个必然的环节.”错题,既是学生积累学习经验和学习资料的宝库,又是教师发现教学问题、改进教法、及时调整教学策略的重要手段[2].因此,利用好错题资源,分析产生错误的原因,总结解题经验,就一定能提高数学解题水平.

