基于ADRC的永磁同步电机速度环控制器设计方法

陶海莉 高孝君

（1.广东美的暖通设备有限公司 佛山 528311；2.佛山鸿威技术有限公司 佛山 528311）

引言

永磁同步电机具有动态性能好，效率高等优点，在工业领域、民用领域有着越来越多的应用[1]。基于矢量控制方法，将其控制方式等效为直流电机，获得更好的控制效果和性能。永磁同步电机的控制系统由电流环和速度环构成，并采用PI控制器结构[2]。PI控制器虽然具有结构简单，调试方便等优点，但是其本质是“基于误差的反馈来消除误差”，对于系统的扰动以及模型变化等，其控制性能将受到限制。预测控制、自适应控制等现代控制方法在永磁同步电机控制系统的应用受到广泛的关注。但是，自适应预测控制算法复杂，对处理器的性能要求较高；预测控制算法存在模型预测精度不高、滚动优化策略少、反馈校正方法单调等问题[3]。

自抗扰控制器（active disturbance rejection controller,ADRC）是一种新型的控制方法。该控制器通过对整个系统的内外扰动进行实时估计，并进行动态补偿，结合设计合适的控制律，从而使得系统获得更好的鲁棒性和动态性能[4-7]。虽然自抗扰控制器（ADRC）在永磁同步电机应用上存在不少的研究成果[8-12]，但是其控制结构复杂，参数整定困难等特点，限制了应用范围。

为了降低自抗扰控制器的设计难度，本文研究了一种基于ADRC的永磁同步电机速度环控制器设计方法。将电机的参数变化以及内外扰动扩张为二阶变量，构建系统的扩张状态观测器（extended state observer, ESO）。将扰动量前馈补偿，使得系统等效为串联积分环节。基于扰动补偿后的系统模型，设计状态误差反馈控制律（state error feedback control law）。为了提升系统的动态性能，引入了基于跟踪微分器（tracking differentiator，TD）的前馈控制器。控制系统的整定参数依赖于系统转动惯量，本文引入了基于扩张状态观测器的转动惯量辨识方法。

通过MATLABSIMULINK搭建仿真模型和永磁同步电机控制器实验环境，验证控制器设计方法的有效性，并和PI控制器的矢量控制系统进行对比研究。实验以及仿真的结果均表明，ADRC的动态性能以及抗扰动性能优于PI控制器。

1 永磁同步电机动力学模型

基于转子磁链定向的矢量控制理论，永磁同步电机在忽略高次谐波影响，并进行同步坐标旋转变换可得电压-电流方程组如下所示：

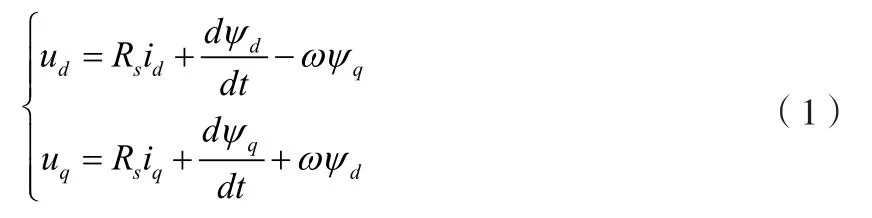
式中：

uq、ud、id、iq—定子侧电压电流；

Rs—定子电阻；

ω—电气角速度；

ψd、ψq—磁链。

使用d-q电流解耦控制，并基于典I型设计的电流环控制器，在考虑控制器以及功率逆变电路上的延时，可以等效为一阶惯性环节。

式中：

TΣi—电流环控制器的总延时，包含PWM更新、电流采样滤波器等；

使用标幺化的运动方程如下所示：

式中：

nN—永磁同步电机的额定转速；

n*—电机转速；

Kt—转矩系数；

TL—负载转矩；

J—系统的转动惯量；

B—系统粘滞系数；

2 转速环自抗扰控制器设计

由于电流控制带宽较高，通常采样PI控制器可以满足性能要求。速度环作为外环，控制带宽相对较低，且需要面对复杂的外界工况，结合自抗扰控制原理，构成了如图1的控制方案。一阶自抗扰控制器主要由跟踪微分器（tracking differentiator，TD）、扩张状态观测器（ESO）以及线性状态误差反馈控制率（state error feedback control law，NLSEF）。自抗扰控制器的跟踪微分器使系统的过渡过程更加平缓，无超调。采用扩展状态观测器对系统的扰动及参数变化进行补偿，提升系统的抗扰性能。

图1 基于ADRC的永磁同步电机速度环控制框图

2.1 扩张状态观测器设计

将式子（3）中的永磁同步电机动力学方程变形成如式子（4）所示。其中a(t)为系统的干扰项，包含了负载转矩以及摩擦力等非线性特性。

将系统扩展成二阶，并根据系统模型设计扩展观测器，如下公式（5）所示。

其中b为：

当t→∞时，扩展状态观测器的扩展状态z2收敛于如下式所示：

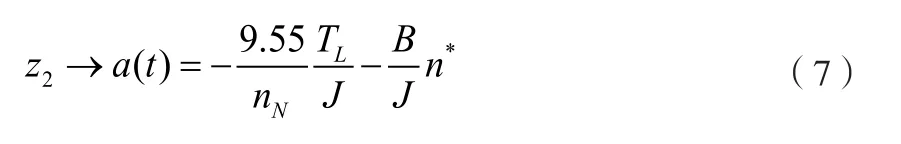
根据式子（5）所示，扩展状态观测器的输入值为转速n*和q，输出值通过状态反馈到电流环的输入端。

永磁同步电机的电流环传递函数表达式等效为式（8）所示。

引入扩张状态观测器后，电流环的控制器输入将满足如下关系是：

电流环的频带宽度远大于机械环节的频带宽度。因此在机械环节的频带宽度内，可将电流环等效为低通滤波器并视为为直通环节 结合式（4）、（8）和（9）表达式，实现对扰动量进行全补偿，速度环的被控对象可以简化为一阶积分环节，有助于系统的设计，提高系统的稳定性以及抗扰性能。

使用后向差分方法对转速环扩张状态观测器进行离散化，有利于在计算机系统上实现。其中h为系统的离散化步长。

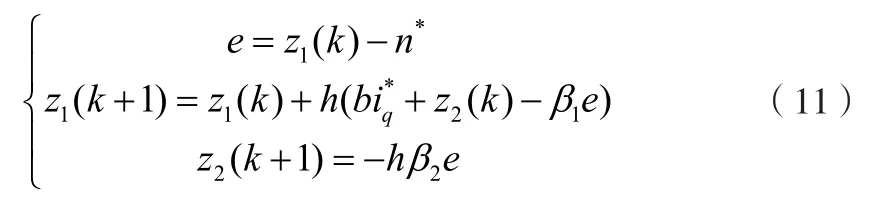
对公式（5）进行拉普拉斯变换，并使β1=2ω0，可得式（12）。

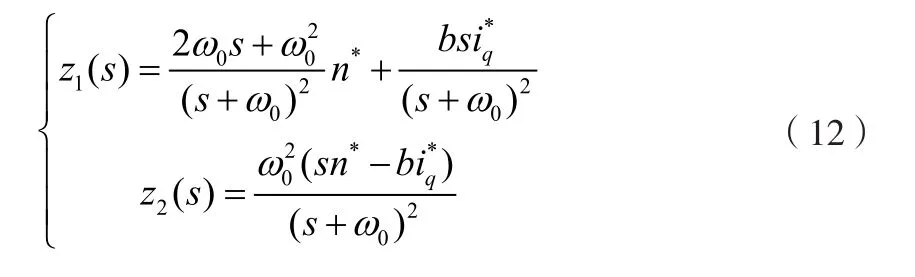
将扩展状态观测器同控制系统结合后，根据公式（12）和图2的结构，系统传递函数模型如图3所示。其中a(s)为扰动量传递函数表达式。

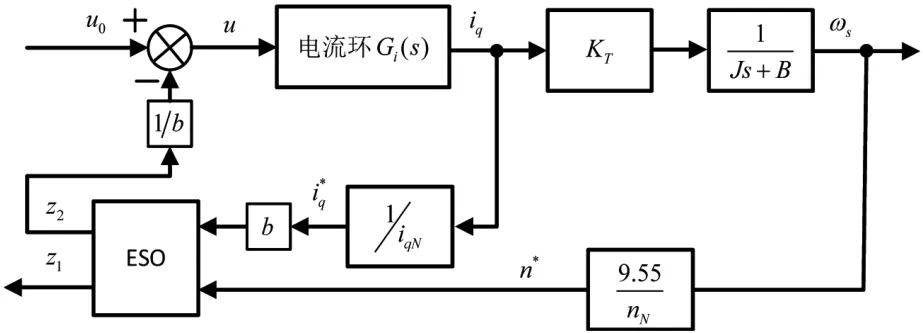
图2 加入扩张状态观测器的转速环控制结构图

图3 加入扩张状态观测器后的扰动模型

根据系统框图，可得扰动量通道的传递函数表达式为：

当扰动信号为阶跃信号时，式（13）的总扰动量将接近0，如式（14）所示。

当扰动信号为斜坡信号时，系统的总扰动量将存在一个静态的误差值。

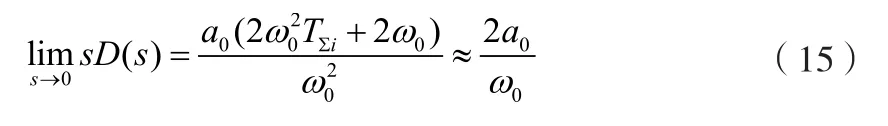
不引入扩展状态观测器时，系统的稳态误差为：

将扩张状态观测器设计成二阶共零点的形式，将保证系统的快速性和稳定性。并能够对于阶跃信号扰动保持无静差跟踪。根据以上设计，提升了系统的抗扰动性能。

2.2 控制器设计

根据“分离原理”，速度环控制器和扩展观测器单独设计，就能够满足系统的稳定性需求，不存在相互耦合的关系。

（1）线性状态反馈控制律

将电流环等效成一阶惯性环节，控制环路结构简图如图4所示。

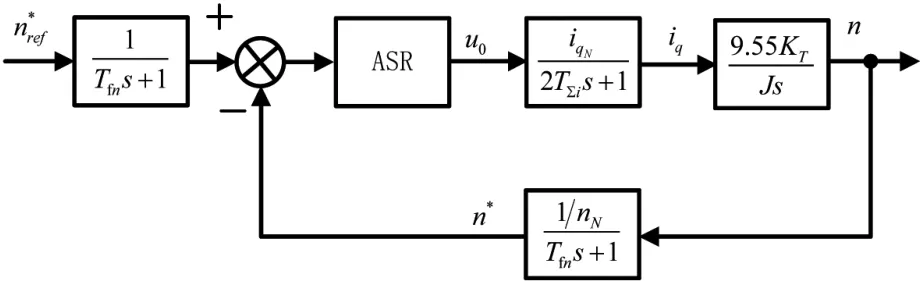
图4 转速环控制结构简图

其中反馈回路上的滤波器为：

式中：

Tfn—转速反馈环路等效延时。

将永磁同步电机的速度环为二阶系统，将其控制器设计为典II型。在设计速度环控制器过程中，将系统等效成单位反馈，把控制系统的滤波器提入到前向通道中，如图5所示。将电流环等效闭环传递函数同低通滤波器环节合并，合并后的时间常数为：

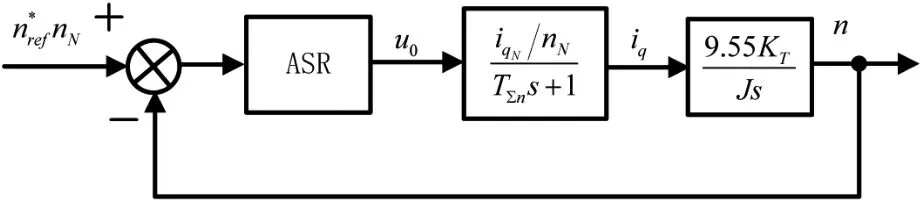
图5 转速环控制框图等效变换

速度环控制器的线性反馈率的传递函数如下式所示：

式中：

Kn—比例系数；

τn为积分时间常数。

因图5的中开环传递函数表达式为：

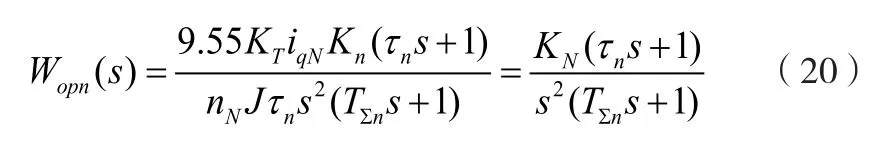
从公式（18）、（19）、（20）中对比可知，基于线性状态反馈控制率的速度环参数如式（22）、（23）所示：

2.3 TD跟踪微分器

引入前馈系统，可以提升系统的动态响应性能，拓宽频带宽度。根据图4控制系统框图，系统前馈表达式如公式（24）所示：

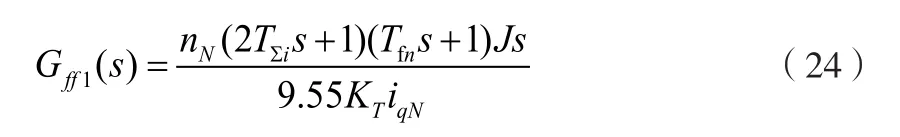
上式（24）是无法通过物理实现分子的阶次高于分母的控制系统。虽然可以通过引入三阶小惯性环节，让系统变为可实现系统，但是引入速度的三阶导数将带来大量的高频干扰，影响系统控制精度，增加系统的损耗。通过忽略高次项，引入一个可调系数kff，增加系统的可靠性和稳定性，可以控制系统的系统简化为：

当系统存在模型不准确时，可以通过可调系数kff使得控制器达到最佳的控制效果，实现系统的部分动态补偿。

系统模型中存在微分项目，使用跟踪微分器（TD）代替微分项，更加快速跟踪微分信号，减少相位滞后，提升噪声抑制能力。

2.4 总结

速度环控制器的结构如图6所示，使用ADRC的控制器，提升系统的快速性。

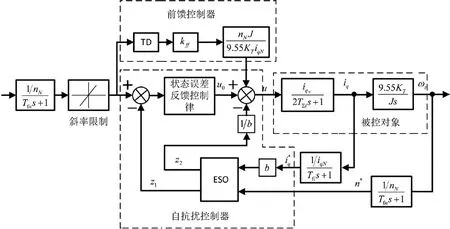
图6 转速环控制结构框图

3 基于扩展状态观测器的转动惯量辨识

永磁同步电机的速度环控制器设计过程中，都包含转动惯量参数。在实际应用过程中，不同的负载将引起转动惯量变化，进而导致控制对象的变化。引起系统的控制性能下降等。考虑转动惯量的变化量∆J，对公式（3）和公式（7）进行重写，

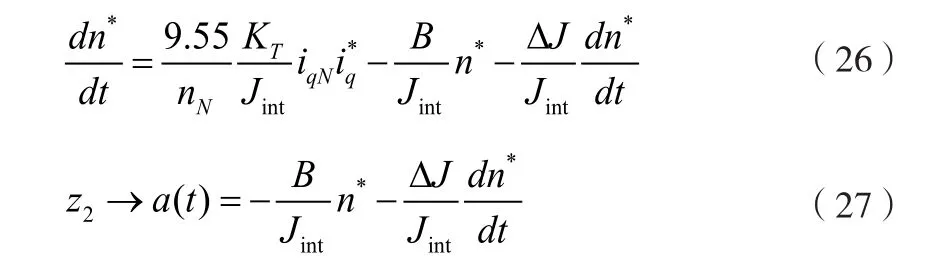
根据式（24）、（25）可知，给定一个转动惯量的初值Jint，并使负载转矩TL=0，线性扩展状态观测器输出值，将包含转动惯量变化值。

通过输入给定的三角波信号源，系统的扩张状态观测器z2的输出如式（27）所示，输出值和转速存在一定的关系。在实际工程中，电机的摩擦系数相对较小。因此摩擦力等非线性力矩，可以忽略不计。对半个周期内的z2进行积分并计算平均值，如式（28）、（29）所示：

将式（28）和式（29）作差，可得：

在给定的三角波信号源中dn*dt的斜率是已知量，对式（30）进行求解，可得：

4 仿真与分析

本文所使用的永磁同步电机的参数如表1所示。

表1 电机参数

根据电机参数，设计电机的转速环以及扩展状态观测器的参数。并基于此，搭建系统的仿真框图，如图7所示。

图7 转速环传递函数仿真模型

仿真结果如图8所示，使用传统PI控制器，在相同的上升时间，基于自抗扰控制器的速度环控制器性能优于PI控制器，具有更小的超调量，更强的抗扰动性能。

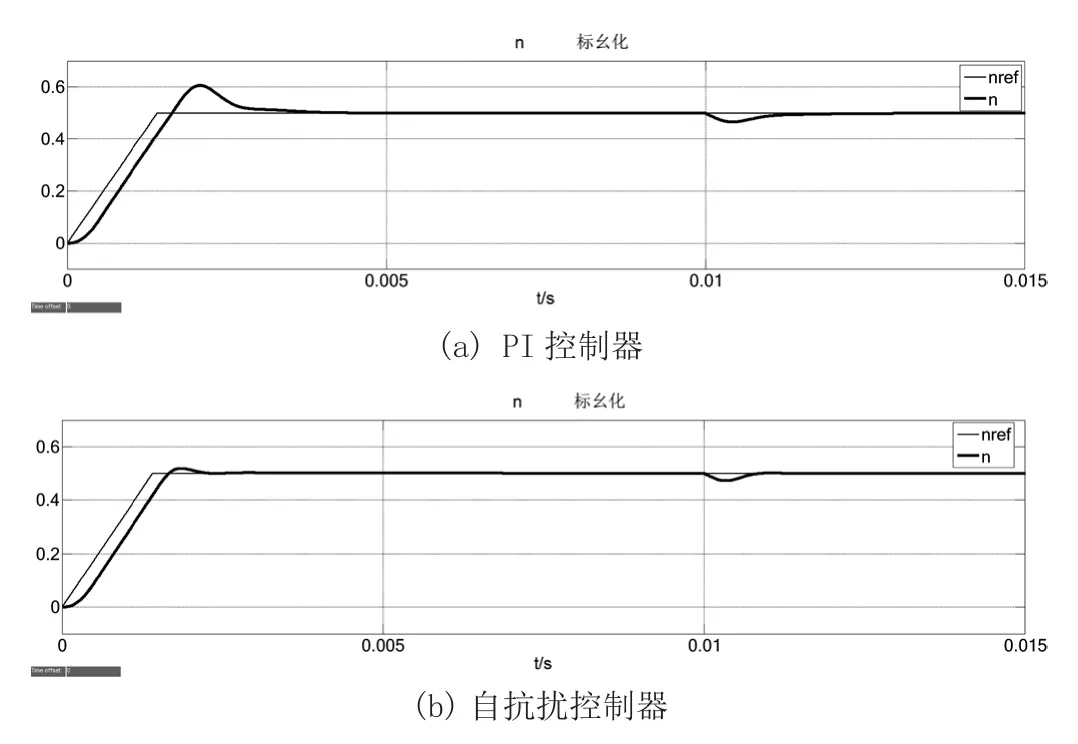
图8 速度环性能仿真对比图

实验电机，加入对拖电机后，转动惯量将发生变化。在仿真系统中，加入转动惯量变化量，输入转速激励信号，扩展状态观测器的输出波形如同图9（b）所示。最终转动惯量收敛于有真实值。

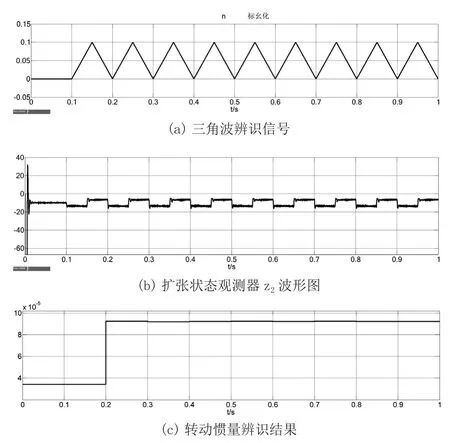
图9 转动惯量辨识仿真波形图

5 实验

本文所使用的实验平台如图10所示。该实验平台包含永磁同步电机及其控制系统以及简易的对拖平台，被拖动电机为安川400 W电机及其驱动器，并使用自研的开发的上位机获取实验波形图。

图10 永磁同步电机控制系统实验平台

实验平台上，速度环的惯量包含了实验电机、联轴器以及对拖电机的转动惯量。速度环控制器设计时，需要考虑以上全部惯量值。因此，使用本文提出的转动惯量辨识方法，实验波形如图11所示。

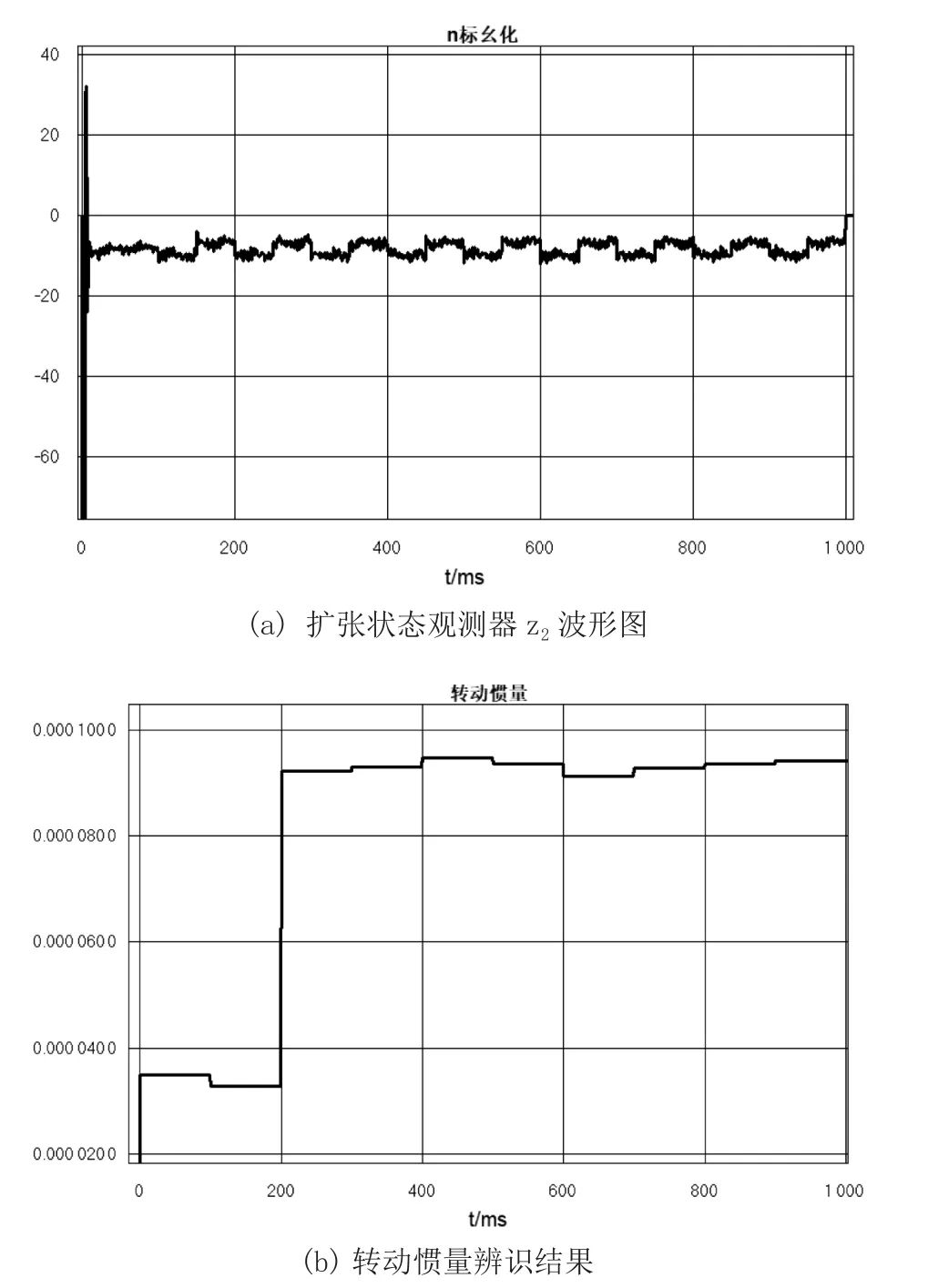
图11 转动惯量辨识实验波形图

传统PI控制器的实验结果如图12（a）所示。启动过程中，系统存在超调量，并且恢复时间更长。在突加负载实验时，PI控制器的最大调节量为3.14 %，转矩变换的时间响应为2.42 ms；自抗扰控制器的最大调节时间为2.23 %，转矩变换的时间响应为1.37 ms，控制系统有更强的抗扰性能。

图12 速度环控制器实验波形图

6 结论

本文从理论出发，通过分析自抗扰控制器的传递函数以及永磁同步电机速度环的数学模型，得到了永磁同步电机扩张状态观测器、反馈控制律以及TD微分器的设计方法。通过仿真与实验，验证了设计方法的有效性和可靠性。通过对比验证，基于ADRC的永磁同步电机速度环控制器，具有更快的响应性能，更强的抗扰动性能。