致密砂岩气藏射孔完井裂缝起裂压力研究
杨喜萍,胡景宏,付 亮,廖松泽
(1.中国地质大学(北京)能源学院,北京 100083;2.非常规天然气地质评价与开发工程北京市重点实验室,北京 100083;3.中国石化石油工程技术研究院有限公司,北京 102206)
致密砂岩储层裂缝起裂受到井眼轨迹、地应力场、注入压力等多种因素影响[1-2]。在上世纪六十年代到九十年代,国内外学者Yew等[3-7]通过研究井筒周围应力场的分布,系统提出了早期运用广泛的水力压裂裂缝起裂模型。1995年,陈勉等[8]给出了斜井井筒周围应力场计算模型和裂缝起裂新判据,认为注入流体和压裂液会对井筒产生轴向上的拉应力,并给出了修正系数的取值范围,但其物理意义不明确。2000年,Hossain[9-10]通过对射孔孔道应力集中现象进行分析,推导出目前普遍运用的井筒破裂压力计算公式,但其并未考虑压裂液滤失效应及孔压所造成的影响。进入21世纪,柳贡慧等[11-21]学者分别从不同角度对水力压裂裂缝起裂模型进行改良和补充,以期扩展应用领域及提高精确性。
鉴于目前国内外对于致密砂岩气藏射孔井筒周围应力场的分布并没有统一标准,本文通过分析国内外学者所提出的应力分布计算模型,结合实际压裂情况,考虑施工注入流体对井壁的作用、压裂液滤失现象和孔隙流体压力的影响,应用岩石力学、弹性力学相关理论知识,建立新的致密砂岩气藏射孔完井方式下井筒及射孔孔道表面应力分布模型(以下简称新模型),以期为准确预测目标储层裂缝起裂压力提供理论基础和依据。
1 井筒周围应力场理论分析
对井筒周围岩石进行受力分析首先应建立合适的数学模型,建立岩石受力数学模型过程中要综合考虑地层岩石的力学环境和施工情况[1]。地层岩石实际受多个因素影响,包括地层岩石所受的地应力、岩石中的孔隙流体压力、注入流体压力、压裂液滤失引发的应力变化和射孔完井在孔眼附近的应力集中等[6]。为便于后续模型建立与分析,作以下三点假设[2]:①岩石均匀且各向同性,为理想地质体模型;②岩石为满足线弹性的多孔介质;③岩石与注入流体之间不发生任何复杂反应。
为方便推导应力场公式,本文根据岩石的受力情况把地层原主应力简化为三个沿着直角坐标系主方向的等效应力,即沿水平方向的最大主应力(σH)和最小主应力(σh),沿重力方向的垂向主应力(σv)[5]。通常在莫尔-库仑剪切破坏理论的基础上,根据三个地层原主应力的相对大小把地层应力系统分为三类,分别是正断层(σv>σH>σh)、走滑断层(σH>σv>σh)和逆断层(σH>σh>σv)[22]。假定在地层中存在某井筒,其井斜角为φ、方位角为β,为方便对储层岩石进行受力分析,按照原地主应力σH、σh、σv的方向建立坐标系(1,2,3),然后通过坐标旋转一定角度建立井筒直角坐标系(x,y,z)和柱坐标系(r,θ,z),求得储层岩石原地主应力场[5]的分布(图1)。
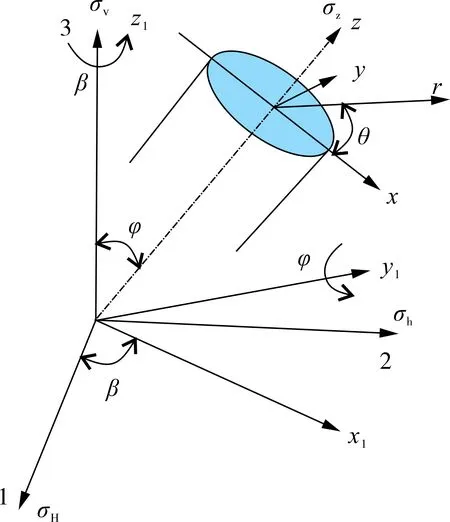
图1 井筒各坐标系间的变换关系
原地主应力在井筒直角坐标系(x,y,z)中的正应力和剪切应力分量分别为:
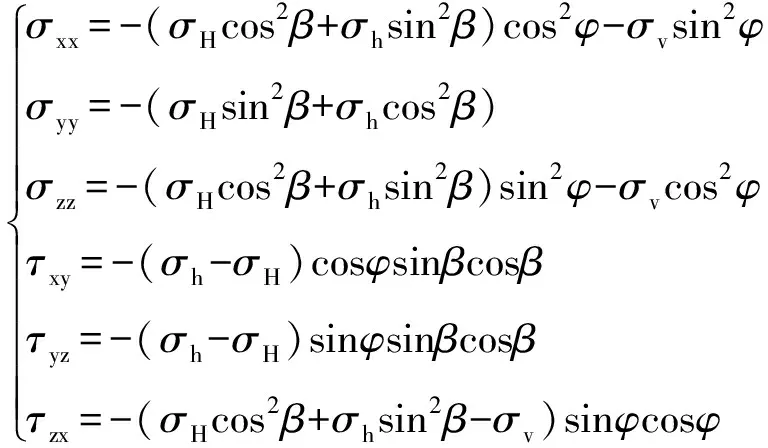
(1)
式中:σxx、σyy、σzz分别为直角坐标系主方向上的正应力分量,MPa;τxy、τyz、τzx分别为直角坐标系主平面上的剪应力分量,MPa。
1.1 射孔井筒周围岩石受力的应力场分布
基于前人在井筒应力分布模型上所做的工作,结合实际压裂情况,在岩石受到的原地主应力所产生的应力分量的基础上,又考虑施工注入流体对井壁产生的应力和压裂液在地层中通过渗透滤失所导致的应力变化(本文拉应力为正),对井筒周围的应力分布进行分析。
1.1.1 井筒注入流体对井壁产生的应力
在储层岩石压裂施工的过程中,井筒注入流体会产生井壁应力场,这种情况在裸眼井或者射孔井中都有存在。因此,必须充分考虑施工过程中井筒注入流体对井壁所产生的应力,在柱坐标系内其应力分量可表示为:
(2)
式中:σr、σθ分别为井筒径向应力、切向应力,MPa;r为目标点到井轴的距离,m;R为井壁半径,m;Pw为井筒内注入流体压力,MPa。
1.1.2 压裂液在地层中滤失产生的应力
在地层压裂作业过程中,若满足以下两个条件:①地层中存在滤失孔隙及相应存储空间;②存在驱动流体的压差;压裂液就会由于压差作用而产生滤失。在分析压裂液滤失引起的应力变化时,本文作了两点假设:①岩石为多孔弹性介质;②流体流动为达西流动[2]。由于裂缝中的注入流体压力高于地层孔隙压力,压裂液通过地层孔隙产生滤失,并且随着注入压力升高,滤失量逐渐增大。故由于压裂液的滤失效应而引起的应力分量变化在柱坐标系内可表示为:
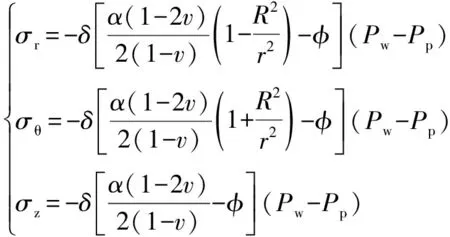
(3)
式中:σz为井筒轴向应力,MPa;α为波尔特多孔弹性系数;v为泊松比;φ为岩石孔隙度;δ为渗透性系数;Pp为地层初始孔隙压力,MPa。
基于前人的计算模型[2,5],考虑以上相关应力,由迭加原理可以推导出柱坐标系下射孔井筒在未射孔前的周围应力场分布:

(4)
式中:τrθ、τθz、τrz分别为井壁处的剪切应力分量,MPa;θ为作用点所在孔径与σxx方向夹角,°。
由于本文研究的是射孔完井方式,故仅考虑r=R的情况,则式(4)可简化为:
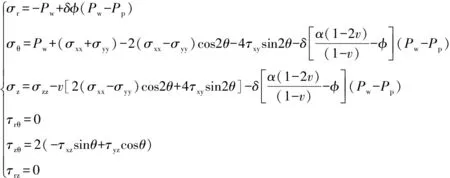
(5)
当不考虑现场施工条件限制、压裂液滤失和孔隙流体压力的影响(即α=0、δ=0、φ=0)时,式(5)可以写为:
(6)
式(6)就是Yew、Hossain等人所建立的斜井井壁应力场分布模型,该模型仅仅是新模型的一个特例,也正好从侧面验证了新模型的合理性和适用性。
1.2 射孔孔眼周围应力场分布模型
相对于裸眼完井,射孔完井的井筒周围,尤其是射孔孔道周围的应力分布要更复杂一些[16]。由于射孔完井的射孔孔道可以等效为一个井筒半径很小、井筒长度很短的微型井,受到两个相互垂直的应力σz和σθ的共同作用,故可以用裸眼井的分析思路去计算射孔井筒孔眼处的应力场(图2)。

图2 射孔孔眼应力分布
按照以上分析,射孔孔眼可以看成一个新的裸眼井筒,为了方便计算,假设射孔井筒与孔眼之间存在良好的水力联通,即具有相同的流体压力[23]。在进行其应力场分析时应以射孔孔道的半径作为新井筒半径,对孔眼井壁处的应力场进行分析与讨论。考虑孔眼引起的应力集中现象[2],基于应力迭加原理即可求出射孔孔眼井壁处的应力场分布:
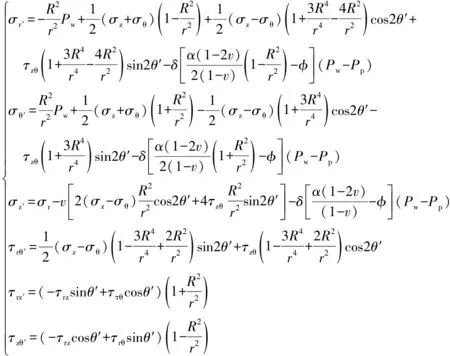
(7)
式中:σr′、σθ′、σz′分别为孔眼井壁处的径向应力、切向应力、轴向应力,MPa;σrθ′、σrz′、σzθ′分别为孔眼井壁处的剪切应力,MPa;θ′为裂缝起裂方位角,°。
当r=R,射孔井筒井壁处的σz和σθ可作为射孔孔道坐标系x′和y′方向上的应力分量,结合式(1),即可得到射孔孔眼井壁处的应力场分布:
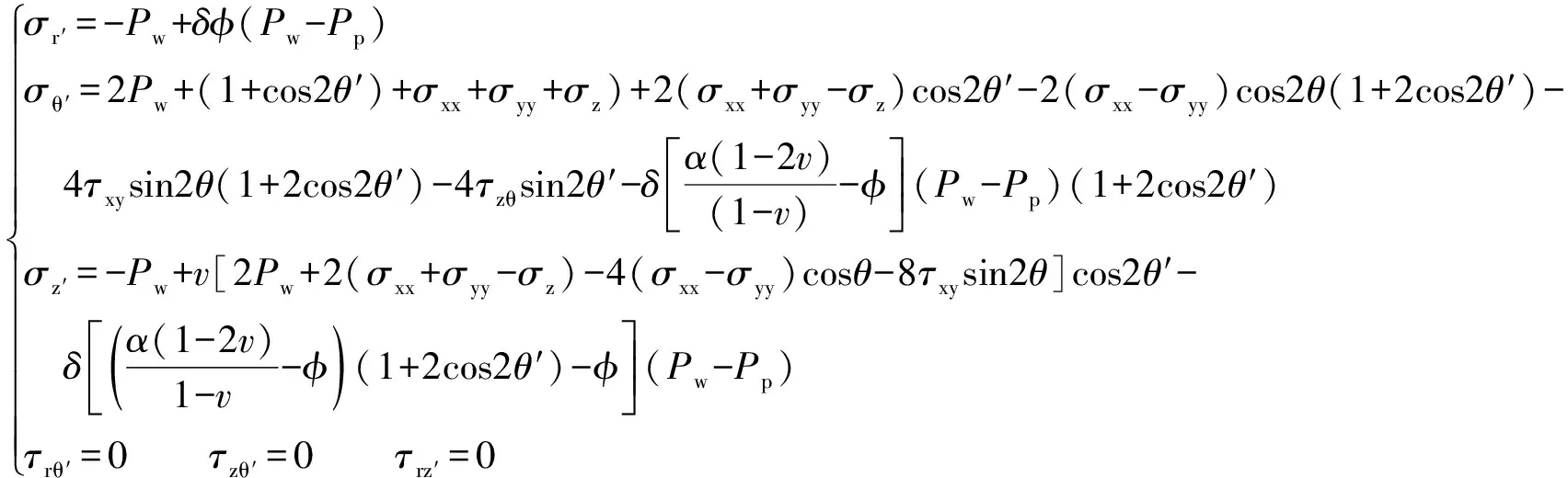
(8)
1.3 模型模拟与讨论
为观察并验证新模型的正确性和适用性,选择模拟参数如下:σH=45 MPa,σh=30 MPa,σv=40 MPa,Pp=18 Pa,Pw=53 MPa,α=0.65,v=0.25,φ=0.1,δ=1。由前文分析及建立的应力分布模型可以看出,井筒周围岩石的受力情况是非常复杂的,又因为同一岩石的抗压强度远高于其抗拉强度,故本文采用岩石的最大拉应力理论。
1.3.1 射孔井筒井壁处的应力场
根据岩石力学、弹性力学相关理论知识,忽略推导过程,直接给出井壁处任意点的三向主应力计算表达式(式(9))。由于本文拉应力为正,故σ2就是与裂缝起裂相关的周向最大应力σmax。
(9)
根据新模型模拟并计算出未射孔的射孔井筒随着井斜角的变化井壁处最大周向应力的值(图3)。

图3 最大周向应力随井斜角变化关系
当井斜方位角(β)固定时,随着井斜角(φ)的变化井壁表面的最大周向应力值不断变化,但井壁处出现最大周向应力值所对应的θ值并不变。这就可得出一个结论:井斜角并不能影响裂缝的起裂方位,但可通过影响井壁表面的最大周向应力值而影响井筒起裂压力。
当井斜角(φ)固定时,随着井斜方位角(β)的变化,井壁处最大周向应力值所对应的θ值也在不断变化,且二者成互补关系。这就可以得出另一个结论:井筒的井斜方位角决定着裂缝的起裂方位角。该结论可为后文的井筒射孔提供一定的理论支持。
1.3.2 射孔孔眼井壁处的应力场
根据岩石力学、弹性力学相关理论,直接给出考虑集中应力后计算得到的孔眼周围最大周向应力为:
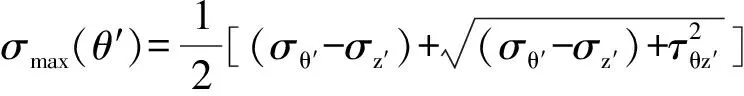
(10)
根据新模型,考虑不同射孔方位,即θ值不同,模拟计算出射孔孔眼井壁处的最大周向应力(图4)。
当射孔井筒在β=0°、θ=0°、射孔时,裂缝起裂方位角为0°时孔眼井壁处的周向应力值最大,此时岩石也最容易破裂。
当β=0°、θ=0°和β=0°、θ=30°时,σθ起主要作用,主要形成纵向裂缝,而井筒注入压力通过影响σθ′进而影响井筒周向应力值,此时最佳起裂方位角为0°。当β=0°、θ=60°和β=0°、θ=90°时,σz起主要作用,有可能形成横向裂缝,而此时原地主应力通过影响σz′进而影响井筒周向应力值;图4c、4d中起裂方位角为45°左右时出现转折是因为由注入压力Pw起主要作用转化为由原地主应力起主要作用所引起的,此时裂缝最佳起裂方位角为90°;而由原地主应力所决定的最大周向应力一直为负数(即压应力),跟前文所述采用的张性破裂准则相悖,故射孔孔眼的最佳起裂方位角应为0°。

图4 射孔孔眼井壁最大周向应力随射孔方位变化关系
孔眼存在所导致的应力集中,使得孔眼井壁处的应力比井筒井壁处的应力大幅度提高,即在相同条件下使地层发生破裂时,射孔井相对于裸眼井所需要的起裂压力要低很多,这符合实际情况。
2 射孔井裂缝起裂压力
2.1 射孔井起裂压力理论分析
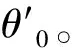
基于岩石最大拉应力理论,同时考虑孔隙流体压力对井筒围岩起裂的影响,当孔眼井壁z′-θ′平面上的有效拉应力满足式(11)时,岩石发生断裂,此时的注入流体压力即为岩石的起裂压力Pw。
(11)
式中:ηp为孔隙压力贡献系数;σt为岩石抗拉强度,MPa。
2.1.1 射孔垂直井筒起裂压力分析
射孔垂直井筒,井斜角(φ)为0°,方位角(β)为0°,此时σxx=-σH、σyy=-σh、σzz=-σv、τxy=0、τxz=0和τyz=0;为使射孔孔眼与预计的裂缝方向相同[24],结合新模型,沿σH方向射孔(θ=0°)为最佳射孔方位;同时对式(10)进行求导可知,裂缝的起裂方位角(θ′)为0°或90°。
当起裂方位角为90°时,由新模型所得到的切向应力主要形成横向裂缝,而横向裂缝的破裂与井筒流体压力并无太大关系,主要受地层主应力影响。对于正断层或者走滑断层,横向裂缝可能直接从射孔井筒表面开裂,但极其困难,且跟井筒射孔的初衷相悖;对于逆断层,直接从井壁开始横向断裂几乎是不可能的[10]。当起裂方位角为0°时,所得到的切向应力主要形成纵向裂缝,且对于预计的裂缝方向是有效的,故本文只考虑起裂方位角为0°这一种情况。从图4得出的结论验证了这个观点,而这也刚好证明了新模型的正确性。
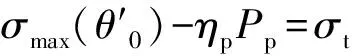
当σθ′≥σz′,即σmax=σθ′时,
(12)
当σθ′<σz′,即σmax=σz′时,
(13)

2.1.2 射孔水平井筒起裂压力分析
(1)水平井筒轴线沿σH方向,井斜角为90°,方位角为0°,此时σxx=-σv、σyy=-σh、σzz=-σH、τxy=0、τyz=0和τzx=0;为使孔眼与预计的裂缝方向相同,结合新模型及地应力关系,最佳射孔方位(θ)可能为0°(正断层或走滑断层,沿σv方向)或者90°(逆断层,沿σh方向)。本文以走滑断层(σH>σv>σh)为例,结合图3得出的结论可知,最佳射孔方位(θ)为0°;与前文垂直井筒推导相似,当起裂方位角(θ′)为0°时,将以上数据带入式(8)并根据岩石张性破裂准则,将σmax=max(σθ′,σz′)带入,即可得出裂缝的实际起裂压力Pw。
当σθ′≥σz′,即σmax=σθ′时,
(14)
当σθ′<σz′,即σmax=σz′时,
(15)
(2)水平井筒轴线沿σh方向,井斜角为90°,方位角为90°,此时σxx=-σv、σyy=-σH、σzz=-σh、τxy=0和τzx=0;为使孔眼与预计的裂缝方向相同,根据σH>σv>σh(走滑断层)以及图3得出的结论可知,最佳射孔方位(θ)为90°;类似于前文推导即可分别得出裂缝的实际起裂压力Pw。
当σθ′≥σz′,即σmax=σθ′时,
(16)
当σθ′<σz′,即σmax=σz′时,
(17)
2.2 实例与讨论
选取松辽盆地某一致密砂岩油气藏进行模型验证,该井水平段井筒倾斜角为85.6°,采用直径138.6 mm套管并使用水泥固井。该气藏所处地层最大水平主应力(σH)为38.8 MPa,最小水平主应力(σh)为29.2 MPa,垂向主应力(σv)为36.5 MPa,储层岩石的抗拉强度(σt)为3.11 MPa,初始孔隙压力为19.20 MPa,孔隙压力贡献系数为0.72,平均孔隙度0.108,Biot多孔弹性系数为0.68,泊松比为0.25,平均渗透率为16.8×10-3μm2。对该井进行压裂作业时所需的起裂压力约为37.12 MPa。应用新模型和理论编制相应程序,对裂缝起裂压力进行模拟计算,并将结果与Hossain模型进行对比分析(图5)。

图5 Hossain模型及新模型裂缝起裂压力对比
应用新模型,当井筒井斜角为85.6°、井斜方位为0°时,射孔形成纵向裂缝所需的起裂压力为 38.78 MPa,跟实际生产所需压力相差不大,误差仅为 4.45%,在工程误差许可范围内,也进一步证明了新模型的正确性。而Hossain模型结果偏小,误差较大,原因在于Hossain模型没有考虑压裂液滤失效应以及孔隙流体压力对有效应力的影响,从而导致裂缝起裂压力偏低。
3 结论
(1)致密砂岩气藏具有储层物性差、渗透率低、自然产能极低的特征,在地层原地主应力所产生的应力分量基础上,充分考虑施工注入流体压力、压裂液滤失现象和孔隙流体压力等多种因素影响,应用岩石张性破裂准则,建立了具有更高精度的射孔完井方式下裂缝起裂压力和起裂方位的计算模型(新模型),并通过实例验证了新模型的正确性和适用性;新模型的建立对于现场压裂施工设计与开发具有一定的理论指导作用。
(2)井筒的井斜角并不能影响裂缝的起裂方位,但可通过影响井壁表面的最大周向应力值而影响井筒起裂压力;井筒的井斜方位角和地层主应力决定着储层岩石起裂方位角;由于射孔孔眼所导致的应力集中现象,使得孔眼周围的应力大幅度提高。
(3)新模型计算结果表明,地层构造主应力场、井身轨迹参数、射孔方位、完井方式等对裂缝起裂压力均有重要影响。
——以准噶尔盆地玛湖凹陷致密砾岩为例

