基于等几何分析的三维风力机叶片数值仿真研究

汪 泉， 杨书益， 朱晓霜

（湖北工业大学 机械工程学院， 湖北 武汉 430068）

0 引言

目前，有限元分析是研究风力机叶片空气动力学性能最常见的计算方法，但在风力机叶片有限元求解中会遇到几个问题。 一是有限元求解精度与网格的细化程度有关，网格越细，计算结果精度越高，但计算时间和成本也随之增加。 二是网格划分工具对风力机叶片等高级复杂曲面识别精度较低，无法精确划分，会导致计算精度的缺失。三是当风力机叶片模型发生改变，必须重新划分网格，耗费大量时间。 基于以上原因，Hughes T J R 提出等几何分析（IGA）的方法，该方法直接结合了CAD 中的几何模型，将其中的几何信息作为有限元分析的输入信息，大大节省了划分网格的时间[1]。IGA 是基于有限元分析方法的等参单元思想，是将CAD 中用于表达几何模型的非均匀有理B 样条的基函数作为形函数，实现了CAD 到CAE的无缝结合。

许多学者对IGA 进行了研究。 陈明飞基于一阶剪切变形理论，并采用等几何有限元方法对任意曲率的功能梯度曲梁进行了自由振动分析[2]。王悦提出了一种基于T 样条曲面的变网格柔性系统等几何分析方法，形成了系统的T 样条单元局部细化算法[3]。 荣吉利研究了IGA 中的HB 样条基函数构造以及多层贝塞尔提取方法问题， 并通过带圆孔平板静力学算例验证了基于HB 样条IGA 方法的有效性和准确性[4]。刘宏亮针对结构等几何优化设计， 系统梳理和综述了主要的等几何优化方法及其在结构优化设计中的应用[5]。 Deng X W 将Kirchhoff-Love 壳单元用于3D 叶片建模，在基于Rhino 的Grasshopper 中的集成框架进行建模和分析[6]。 Herrema A J 利用IGA 创建了一个优化设计的框架， 用压管为例证实了该框架的实用性[7]。 Aung T L 开发了集成IGA 的优化设计框架， 并将其应用于优化两个焊缝的形状以减少应力集中[8]。

然而以上研究大多基于简单模型的IGA，风力机叶片作为一种高级复杂的曲面， 在等几何方面的应用还很少， 且目前的研究大多是借助三维软件平台的二次开发， 没有实现真正意义上的设计和分析的统一。 为了实现复杂三维风力机叶片设计与分析的完全统一， 避免复杂的网格划分过程，提高其求解精度与效率，本文开展了风力机叶片的IGA 研究。首先构建适合IGA 的风力机叶片NURBS 模型， 然后推导三维静力学IGA 相关计算公式，实现三维复杂风力机叶片的IGA。一方面通过简单算例精确解验证IGA 算法正确性，另一方面通过与商业软件对比验证其优越性。

1 风力机叶片模型的构建

在风力机叶片设计和分析过程中， 设计师通常会先设计其CAD 模型，然后通过有限元分析软件对其进行网格划分。 网格划分的质量决定了仿真分析的精度与效率， 特别对于风力机叶片这种复杂的曲面，容易划分低质量的网格，从而影响分析结果的精度与效率。 为此本文基于NURBS 构建了适合IGA 的风力机叶片二维三维模型，模型设计和分析均采用同一的基函数， 不仅避免了复杂的网格划分过程， 同时也消除了模型设计与分析之间的误差。

1.1 风力机叶片二维翼型的构建

本文将NURBS 作为设计和分析基函数，连接了设计和分析。 一条p 次NURBS 曲线定义为

式中：c（u）为NURBS 样条函数；pi为控制点；wi为权因子；Ni，p（u）为定义在非均匀节点u 上第i 个P次B 样条基函数；a，b 为节点矢量u 的取值范围。

NURBS 曲线具有几何不变性、凸包性和局部支撑性等性质， 是计算机辅助设计系统中最常见的表示方法。 采用NURBS 构建风力机叶片二维翼型可以提高翼型的光滑连续性，可以更准确、更光滑地构建风力机叶片的翼型，为后续的IGA 提供准确的模型支撑。 利用NURBS 来实现风力机叶片翼型的参数化是翼型设计中至关重要的一步，也是IGA 的基础。

在Matlab 中， 先编写翼型反求控制点程序，得到二维翼型的控制点， 然后基于NURBS 理论编写构建翼型程序，其流程如图1 所示。

图1 NURBS 流程图Fig.1 Flow chart of NURBS

首先选择翼型的型值点， 然后通过参数化处理确定样条的阶数，求得节点矢量信息，再通过切矢边界条件，求解线性方程组A*D=E，获得控制顶点向量D， 接着将得到的控制点和节点矢量及权因子作为输入参数，得到NURBS 构建的翼型。图2 为DU97-W-300 翼型分布图。

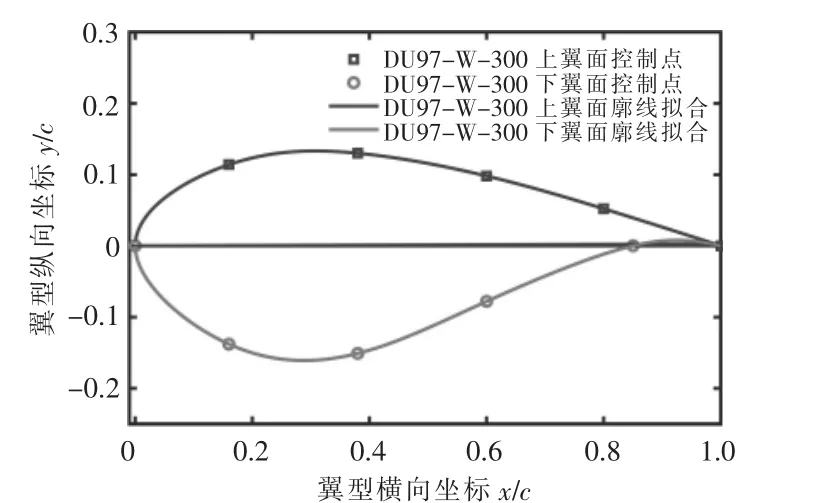
图2 DU97-W-300 翼型分布图Fig.2 DU97-W-300 airfoil

选取了部分型值点，求得其控制点为

1.2 风力机叶片三维模型的构建

叶片是以气动中心轴进行扭转的， 翼型的气动中心为1/4 弦长位置， 一般变弦长变扭角的三维叶片集成表达式为

式中：θ 为幅角；u 为叶片展向位置；ρ（θ）为翼型分布函数；a 为拟合系数；xM为翼型气动中心展向位置，一般取0.25；c（u）为弦长分布函数；β（u）为扭角分布函数。

根据三维叶片的形函数/分布函数公式将其耦合到NURBS 建模中。 分别设置21 个翼型的数据，每个翼型由24 个控制点构成，其中12 个控制上翼型，12 个控制下翼型。

图3 为基于NURBS 构建的三维风力机叶片模型。模型由21 个翼型组成，每个翼型由24 个控制点组成。

图3 风力机叶片NURBS 模型Fig.3 NURBS model of wind turbine blade

2 风力机叶片的IGA

2.1 IGA 方法

设定风力机叶片的材料为各向同性材料，风力机叶片的IGA 属于线弹性问题，风力机叶片在载荷和边界条件下的位移可以表示为边界值问题，其位移ui为

式中：Γ 为域边界；σ 为应力。

式（7）为狄利克雷边界条件，式（8）为纽曼边界条件。

IGA 是对上述式进行变分后得到弱形式，对于边界条件来说，u∈s，v∈V 满足以下条件：

式中：K 为刚度矩阵；P 为载荷向量。

采用高斯积分方法，在得到了位移值之后，可以求得单元的应变ε 为

式中：L 为微分算子。

由此可得应力σ 为

式中：D 为弹性矩阵，与材料的泊松比和弹性模量有关。

IGA 流程如图4 所示。

图4 IGA 流程图Fig.4 IGA flow chart

2.2 NURBS 算例

为了验证NURBS 三维实体IGA 的正确性，首先对简单的算例进行IGA 并与其精确解对比。考虑到受均匀拉力作用下的球形孔洞问题， 算例模型结构尺寸及相关参数如图5 所示。

图5 算例模型结构尺寸Fig.5 Model structure size of the calculation example

图中各参数均为无量纲参数， 其在球坐标系（r，ϕ，θ）的精确解[9]为

式中：a 为球体的半径；S 为施加的拉力；ν 为泊松比。

由于该算例的对称性，本文考虑对模型的1/8 进行IGA，并将计算得到的结果与精确解进行对比。 当S=1，ν=0.3 时，σmax=3S（9-5ν）/（14-10ν），其最大应力精确解为2.045 45。 图6 为球形孔洞的应力云图。 图中IGA 计算得到最大应力值为2.05， 而其精确解为2.045 45， 其相对误差为0.22%。 求解结果与精确解相差无几，通过此算例验证了本文构造的IGA 程序的正确性，为后文风力机叶片的IGA 提供了有效的理论依据。

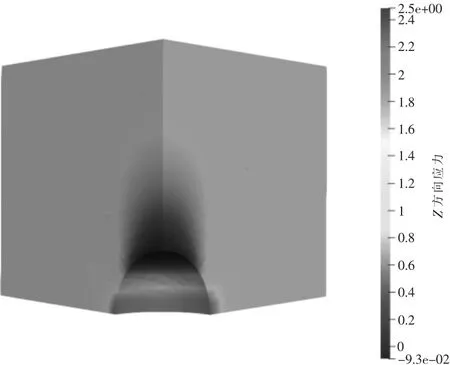
图6 球形孔洞的应力云图Fig.6 Stress cloud diagram of spherical holes

2.3 风力机叶片的IGA

在1.2 节中构建了适合IGA 的三维风力机叶片模型，考虑了叶片的弯扭特性，根据文献[10]，为了方便计算， 将实际风力机叶片模型进行适当简化，将其材料定义为各向同性材料，材料参数设置为弹性模量为1×105MPa，泊松比为0.3，密度为7.8×103kg/m3。

风力机叶片在正常工作时， 其实际受载情况为挥舞方向、拍打方向和扭矩的耦合。本文考虑在风力机叶片挥舞方向受载这一工况下的三维风力机叶片的等几何静力学分析， 根据挥舞方向实际受载情况，其具体约束设置为每个节点的Y，Z 方向固定，X 方向受位移约束-1 mm （图7 中载荷B），将风力机叶片的叶根位置固定。

图7 风力机叶片的模型Fig.7 Model of wind turbine blade

将求解结果输出为.vtu 文件格式， 然后通过将风力机叶片IGA 结果导入开源软件Paraview中进行可视化，得到了风力机叶片的位移云图（图8），在该载荷作用下，其最大位移为2.929 9 mm，最小位移为0.027 5 mm。

图8 风力机叶片位移云图Fig.8 Wind turbine blade displacement cloud diagram

3 结果验证

为了验证风力机叶片IGA 结果的正确性，将计算所得风力机叶片模型控制点信息通过插入曲线命令导入三维建模软件SolidWorks 中进行建模，然后将模型导入软件ANSYS 中构建其有限元模型（图9）。 将IGA 的结果和与有限元分析的结果进行对比，以验证风力机叶片IGA 的正确性。

图9 有限元模型Fig.9 Finite element model

在商业软件ANSYS 中施加与IGA 相同的材料属性、 边界条件和载荷约束， 并进行求解（图10）。

图10 有限元结果Fig.10 Finite element results

为了验证IGA 的正确性，将风力机叶片在相同的条件下进行了有限元分析，叶片在载荷的作用下最大位移为3.012 4 mm，最小位移为0.028 7 mm，IGA 与有限元分析的最大误差为5.1%。 为了进一步验证IGA 的正确性，分别取固定位置处的节点，分析对比IGA 和有限元分析的结果（表1）。从不同位置节点位移的对比结果可以看出，IGA与有限元分析的结果误差均在5.1%以内，进一步验证了IGA 的准确性。

表1 载荷下的位移Table 1 Displacement under load mm

为了验证IGA 的优越性，将不同的控制点数目情况下IGA 的结果与ANSYS 结果进行了对比（图11）。

图11 两种方法不同节点数目的位移值对比Fig.11 Comparison of displacement values of the two methods with different numbers of nodes

当节点数为600 时，IGA 的计算结果为2.8831，计算时间为42 s； 当ANSYS 节点数量为2 300时，计算时间为151 s，其计算结果与IGA 计算结果基本一致。 这也证明了在不损失计算结果精度的条件下，IGA 方法较有限元方法节省了大量的节点，提高了求解的效率。

4 结论

本文针对复杂三维风力机叶片， 首先构建了适合IGA 的风力机叶片NURBS 模型， 然后推导三维静力学IGA 相关计算公式，并编写了相关程序，实现了三维复杂风力机叶片的IGA。并通过简单算例精确解和商业软件对其进行验证， 得到以下结论。

①构建IGA 框架， 并编写相关计算程序，通过简单算例的精确解验证了其正确性。

②将风力机叶片变弦长变扭角公式与NURBS 相耦合， 构建了适合IGA 的三维风力机叶片模型， 并对构建的模型进行IGA， 并将IGA结果与商业软件进行对比。对比结果表明：位移最大误差为5.1%， 验证了风力机叶片IGA 的正确性； 对两种方法在不同节点数情况下的计算结果进行对比，在不损失求解精度的情况下，IGA 较有限元分析节省了大量的节点，提高了求解的效率。