基于电磁-热-流体耦合的隧道敷设电缆载流量分析
石大城,李 乾,余志强,孙晓云,张明志,白英杰,郑海青,韩 广
(1.北京全路通信信号研究设计院集团有限公司,北京 100070;2.国网石家庄供电公司,河北 石家庄 050000;3.石家庄铁道大学a.电气与电子工程学院;b.河北省交通电力网智能融合技术与装备协同创新中心,河北 石家庄 050043)
0 引言
随着城市化程度越来越高,城市用地越来越紧张,对城市电网建设提出了更高的要求。目前比较常见的电缆敷设方式包括排管敷设、地下直埋敷设、隧道敷设等[1]。相比于排管敷设和地下直埋敷设,电缆隧道敷设具有便于检修、便于管理、能够实现多回路电缆集群敷设等优点而被广泛应用在城市电网建设中。随着电缆隧道敷设使用越来越广泛,隧道内空气流速、空气温度等对各回路电缆载流量的影响引起了研究者们的广泛关注[2]。
目前电缆载流量主要通过IEC 60287:2011规定方法和有限元法进行计算[3-4],对于隧道敷设的电缆,IEC 60287:2011标准将其等效为空气敷设且不受阳光直射的条件来计算电缆载流量[5-6],该标准可以快速对电缆载流量进行计算,但其计算的值相对保守,且考虑条件单一[7]。朱攀勇等[8]使用有限元法分析了直埋电缆载流量的影响因素;梁永春等[9]建立地下电缆群温度场有限元模型,对地下电缆群载流量和温度场进行了分析研究;乐彦杰等[10]建立了耦合场仿真模型,对多回路排管敷设电缆载流量进行了研究;郑文坚[11]建立了空气敷设耦合场仿真模型,其研究方法具有一定的借鉴意义。
这些对隧道敷设电缆载流量的研究大多采用二维模型,不能精确模拟隧道内强制对流换热过程。为了更精确地研究电缆隧道敷设下各因素对电缆载流量的影响,本研究建立电缆隧道敷设下电磁-热-流体多物理场耦合的三维有限元模型,与二维模型相比增加了隧道内强制对流换热过程,更加贴近隧道内空气流动,并能直观地观察电缆的径向传热。通过建立的仿真模型研究隧道空气温度、空气流速、水平排列相间距、通风口长度等因素对隧道敷设下电缆载流量的影响规律,根据实际工程数据和检修人员经验数据,设计正交实验研究各影响因素对电缆载流量影响程度的大小,为电缆隧道敷设提供建议。
1 模型介绍
由于隧道深埋于地下,本文建立电磁-热-流多物理场耦合三维模型,忽略地表与空气对流换热对电缆载流量的影响。
1.1 模型几何参数以及电缆参数
模型尺寸设置:隧道横截面长为2.9 m、宽为2.8 m,混凝土厚度为250 cm。采用型号为YJLW03-64/110 1×1 200 mm2的单芯电缆,在模型中共敷设8条回路高压单芯电缆,根据《国家电网公司电缆敷设典型设计技术导则》,电缆中间过道宽度为1.5 m,电缆上下每层间距为400 mm。隧道及电缆分布几何模型如图1所示。

图1 隧道及电缆分布示意图Fig.1 Schematic diagram of tunnel and cable distribution
1.2 物理场模型
1.2.1 电磁场模型
输电线路在输电过程中,通入缆芯的交流电会产生交变磁场,在磁场的作用下,电缆各层会产生电磁损耗,主要存在于缆芯和金属护套。缆芯和金属护套电导率温度函数如式(1)所示,电缆各层损耗如式(2)~(4)所示[12]。

式(1)~(4)中:R20为20℃时导体电阻率,Ω·m;α20为导体的电阻率温度系数,K-1;θc为变化的温度值;ω为角频率,rad/s;A为各层的矢量磁位,Wb/m;σ为材料的电导率,S/m;μ为磁导率,H/m;J为各层电流密度,A/m2;Js为源电流密度,A/m2;P为各层单位长度损耗功率,W/m;S为横截面积,m2。
1.2.2 热场模型
电缆各层损耗可视为热场中的热源,在热场中存在有热源区域包括缆芯、金属护套等和无热源区域包括电缆其余部分、土壤等,电缆敷设在隧道内还存在与空气的对流换热。对于固体有热源稳态导热微分方程如式(5)所示,无热源稳态导热微分方程如式(6)所示,稳态对流传热方程如式(7)所示[13]。

式(5)~(7)中:T为温度变量,K;q为热流密度,W/m2;λ为导热系数,W/(m·K);u、v、w分别为在x、y、z轴方向上速度分量,单位为m/s;ρ为气体的密度,kg/m3;cp为流体比热容,J/(kg·K)。
对于整个模型的热场计算,还需要指定相应的边界条件,主要有3类边界条件:第1类狄氏边界条件即已知边界温度,第2类纽曼边界条件即已知边界热流密度,第3类为对流边界条件,3类边界条件控制方程如式(8)~(10)所示[14]。

式(8)~(10)中:T为温度变量,K;Tw为给定温度,K;λ为土壤导热系数,W/(m·K);n为边界单位法线向量;qw为热流密度,W/m2;α为地表与空气的对流换热系数,W/(m2·K);Tf为地表空气温度,K。
在本模型中,设置深层土壤温度为第1类边界条件,温度为298.15 K。左右边界为第2类边界条件,其热流密度为0。上边界设置为第3类边界条件,地表空气温度为298.15 K。地表与空气的对流换热系数为10 W/(m2·K)。
1.2.3 流体场模型
在地下隧道中由于布置了通风装置,隧道内空气流动主要为强制对流散热。通过计算雷诺数来选择湍流模型。隧道内空气流动遵循气体自然对流连续性方程、流体动量方程和能量方程,如式(11)~(13)所示[15]。
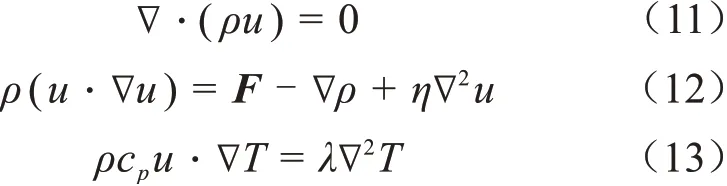
式(11)~(13)中:ρ为流体密度,kg/m3;u为流体的速度,m/s;F为流体单位体积所受的体积力矢量,N/m3;η为流体动力黏度,Pa·s;T为流体介质温度,K;λ为流体的导热系数,W/(m·K);cp为流体比热容,J/(kg·K);∇为拉普拉斯算子。
电缆的电磁损耗为热场中的热源,在Comsol软件中通过设定缆芯和金属护套电导率的温度函数,实现电磁场、热场和流体场之间的直接耦合计算,计算过程如图2所示。
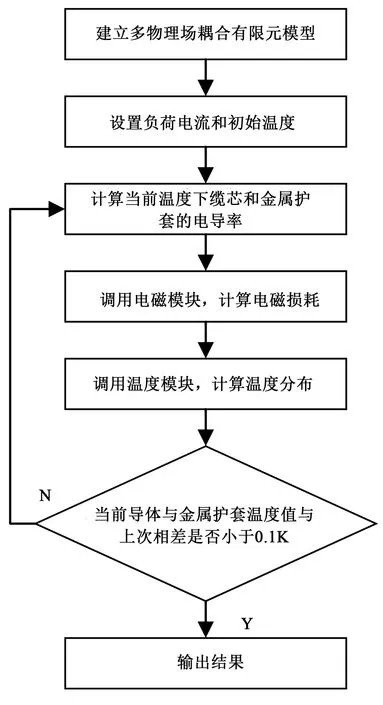
图2 多物理场耦合计算过程Fig.2 Calculation process
1.3 仿真结果分析验证
在IEC 60287:2011中对于隧道敷设电缆载流量的计算等效为空气辐射且不受太阳直射的情况,选用单芯电缆且无铠装层,计算单回路三相水平排列电缆,主要计算公式简化为式(14)。
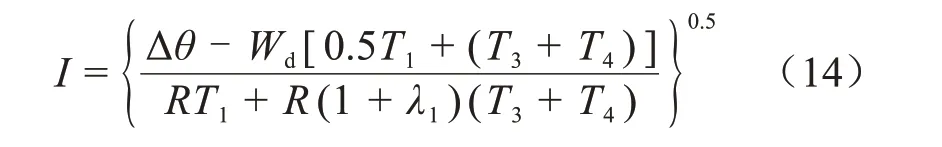
式(14)中:△θ表示缆芯高于环境温度的温升;T1、T3、T4分别为绝缘热阻、外护层热阻和外部热阻;R为缆芯交流电阻;Wd为绝缘层损耗;λ1代表电缆金属套损耗相对于总损耗的比值。
对于式(14)中各个参数的计算,由于公式较为繁多,本文不再一一列举,经计算得出T1=0.944 3,T2=0.095 3,T3=0.751 9,λ1=0.051,缆芯温度最高设为90℃,计算不同环境温度下的电缆载流量。
在模型中将强制对流换热变为自然对流换热,模型中隧道风速设为0,计算结果如表1所示。由表1可知,仿真计算得到的载流量比IEC 60287:2011标准计算得到的值略高,这是因为采用该标准计算出的载流量值相对保守,计算中直接将缆芯温度设为90℃,而在仿真模型中随着温度的变化不断修正电导率和内部损耗,计算结果相对准确。两者相对误差小于3%,符合工程上的使用标准。

表1 仿真计算结果与标准计算结果对比Tab.1 Comparison of simulation results with standard calculation results
为验证本模型的准确性,进行隧道现场实测。选择某段电缆隧道,通过电网公司监控系统得到隧道中敷设电缆的载流量,由于选用隧道为新建隧道,内敷设电缆回路较少,仅敷设了3条回路110 kV电缆,电缆型号为YJLW03-64/110 1×1 200 mm2,电缆内部各层主要参数如表2所示。

表2 电缆几何参数Tab.2 Cable geometry parameters
使用CEM DT-8894型风速仪测量隧道中间位置风速及隧道空气温度,使用DT-9868S型红外热像仪测量电缆表皮温度,选取电缆左、右、上3点取温度平均值作为某条电缆表皮温度。通过实测得出,隧道内空气温度为17.3℃,隧道内风速为0.3 m/s,本次测量位置选在距离通风口6 m处,将实测获得的隧道内风速和空气温度加入到仿真模型中,同时模型中电缆载流量已通过电网监控系统得知,则仿真计算得到的电缆表面温度与实测得到的结果如表3所示。由表3中结果可知,通过仿真计算得到的结果与实测值相差不大,相对误差在允许范围内,说明能够通过本模型进行隧道敷设下电缆载流量的分析计算。

表3 电缆表面温度仿真结果与测量值对比Tab.3 Comparison of cable surface temperature simulation results and experimental values℃
2 隧道敷设下电缆载流量影响因素分析
采用电磁-热-流多物理场耦合三维仿真模型,分析各因素对电缆载流量的影响规律。电缆各层产生的损耗作为模型中的热源,缆芯和金属护套的电磁损耗受电流密度分布的影响会出现集肤效应,其主要损耗出现在导体和金属护套上,如图3所示。

图3 电缆各层损耗Fig.3 Losses at all cable layers
2.1 隧道内空气流速的影响
隧道内空气流速以国网某段电缆隧道实际风速情况进行研究,在强制对流换热条件下,隧道内风速一般不大于0.6 m/s。通过计算得到,风速为0.45 m/s时,隧道内速度分布如图4所示。从图4可以看出,电缆周围空气流速相对较低,而在隧道中部和上方流速较大,这是因为电缆和支架等会阻碍空气流动,造成风速降低,对流换热作用降低,因此在隧道内应尽量减少障碍物,保证空气的充分流动。

图4 隧道内速度分布切面图Fig.4 Cross section of velocity distribution in tunnel
隧道内空气流速与电缆载流量的关系曲线如图5所示。从图5可以看出,载流量随隧道内空气流速的增大而增加,两者近似呈线性关系,风速能够带走电缆散发出的热量,是促进电缆散热的有效手段。因此在高负荷期间可提高风速,在低负荷时可降低风速或者关闭风机使隧道内处于自然对流,降低运行成本。

图5 隧道内空气流速对电缆载流量的影响曲线Fig.5 Influence curve of air velocity in tunnel on the current carrying capacity of cable
2.2 流入隧道空气温度的影响
流入隧道的空气温度会影响隧道内的热场,对电缆的散热产生影响,从而影响电缆载流量。流入隧道的空气温度与电缆载流量的关系曲线如图6所示。由图6可以看出,流入隧道内的空气温度与电缆载流量近似为线性关系,隧道内空气温度每升高1℃,电缆载流量下降约9 A。
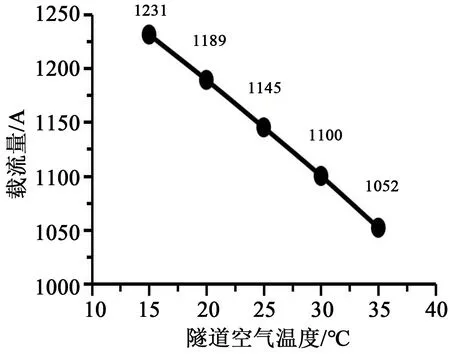
图6 流入隧道空气温度对电缆载流量的影响曲线Fig.6 Influence curve of the air temperature flowing into the tunnel on the current carrying capacity of cable
冬天外部空气较低时,流入隧道内的空气温度较低,可适当降低风机系统风速甚至关闭风机节约资源;夏天时外部空气较高,可通过布置相应制冷机降低流入隧道的空气温度。
2.3 水平排列间距的影响
电缆排列方式主要为水平排列和三角形排列,本文分别对水平排列和三角形排列的电缆载流量进行计算,结果表明水平排列时中间相温度最高,而三角形排列时温度最大值出现在靠近隧道壁面电缆上,在距离电缆隧道相同位置处,水平排列和三角形排列温度场分布如图7~8所示。从图7~8可以看出,水平排列时电缆载流量不会受与隧道壁面距离的影响,而三角形排列与其相反,距壁面越远其载流量越高。由于规定电缆支架长度不超过50 cm,在距壁面最大距离处水平排列载流量仍然要高于三角形排列。
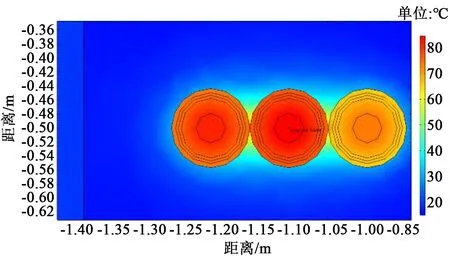
图7 水平排列温度场分布Fig.7 Temperature field distribution in horizontal arrangement

图8 三角排列温度场分布Fig.8 Temperature field distribution in triangular arrangement
通过本模型研究水平排列的电缆间距对电缆载流量的影响,在电缆支架长度不超过50 cm这个限制下,计算110 kV和220 kV电缆不同排列距离对水平排列电缆载流量的影响,两者对应的关系曲线如图9所示。由图9可以看出,同回路电缆排列间距为0时,对电缆载流量的影响最大,随着排列间距不断增大,电缆载流量增长幅度逐渐减小,由于电缆支架长度的限制,两种型号电缆在其排列间距小于电缆半径(110 kV为56.1 mm,220 kV为74.2 mm)时近似为线性关系,当间距大于电缆半径时,其载流量增长幅度越来越小。因此在布置水平排列电缆时应避免电缆紧凑排列,可选择其排列间距为敷设电缆的半径长度,此时对于提高电缆载流量的效果较好。
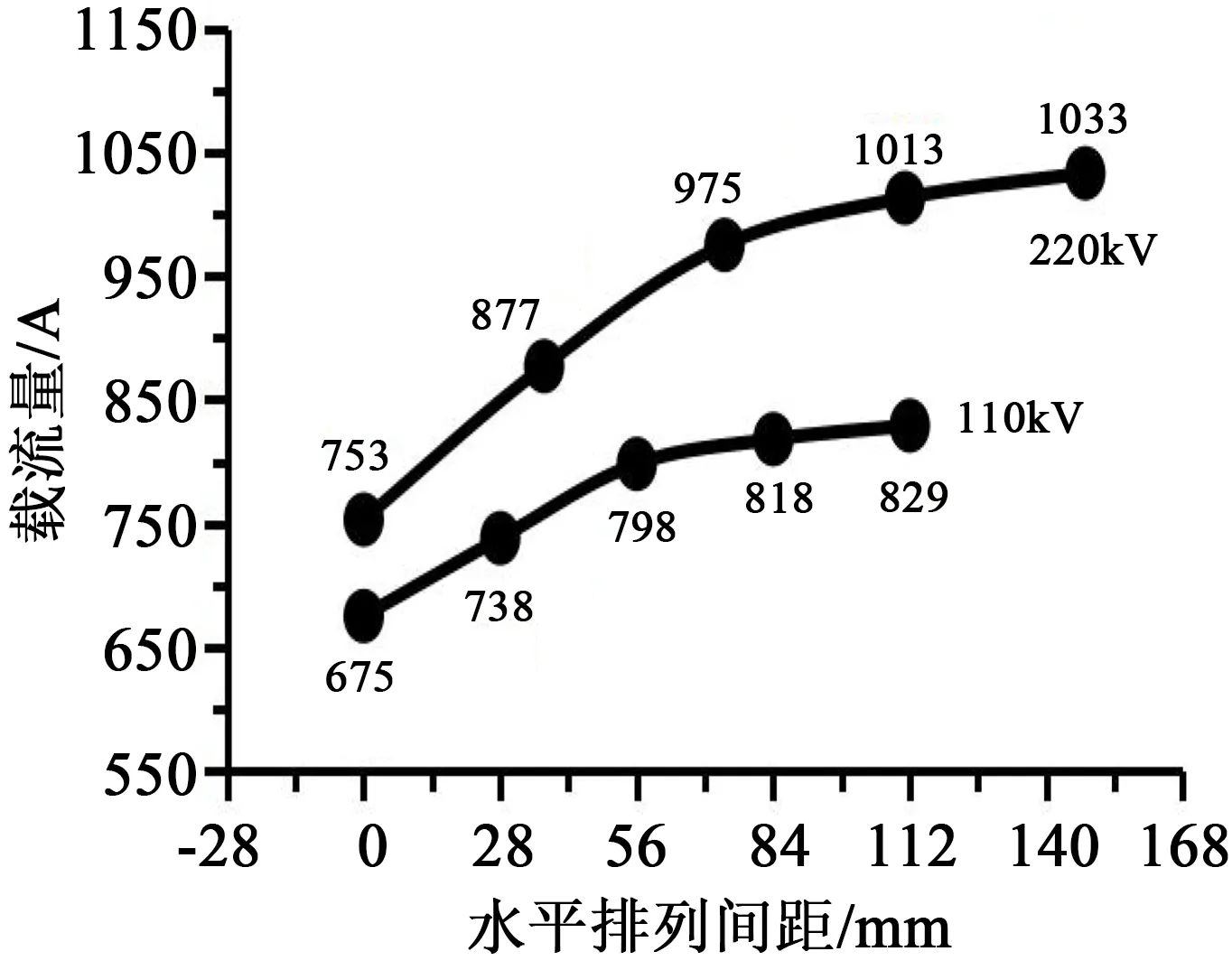
图9 水平排列间距对电缆载流量的影响曲线Fig.9 Influence curves of horizontal arrangement spacing on cable current carrying capacity
2.4 通风口长度的影响
隧道内电缆表面温度分布如图10所示。从图10可以看出,与出口处相比,进口处电缆温度更高。随着隧道长度的增加,温度不断升高,这是由于隧道内存在强制对流换热,空气沿电缆轴向流动将电缆产生的热量不断吹向出口处,隧道内热量随着电缆轴向不断堆积,出口处温度高于进口处温度。以通风口长度为45 m为例,计算相同载流量下单回路电缆表层温度轴向分布,结果如图11所示。从图11可以看出,相同载流量下进风口和出风口处电缆表层温度最大可差20℃,因此需要合理安排隧道通风口长度。
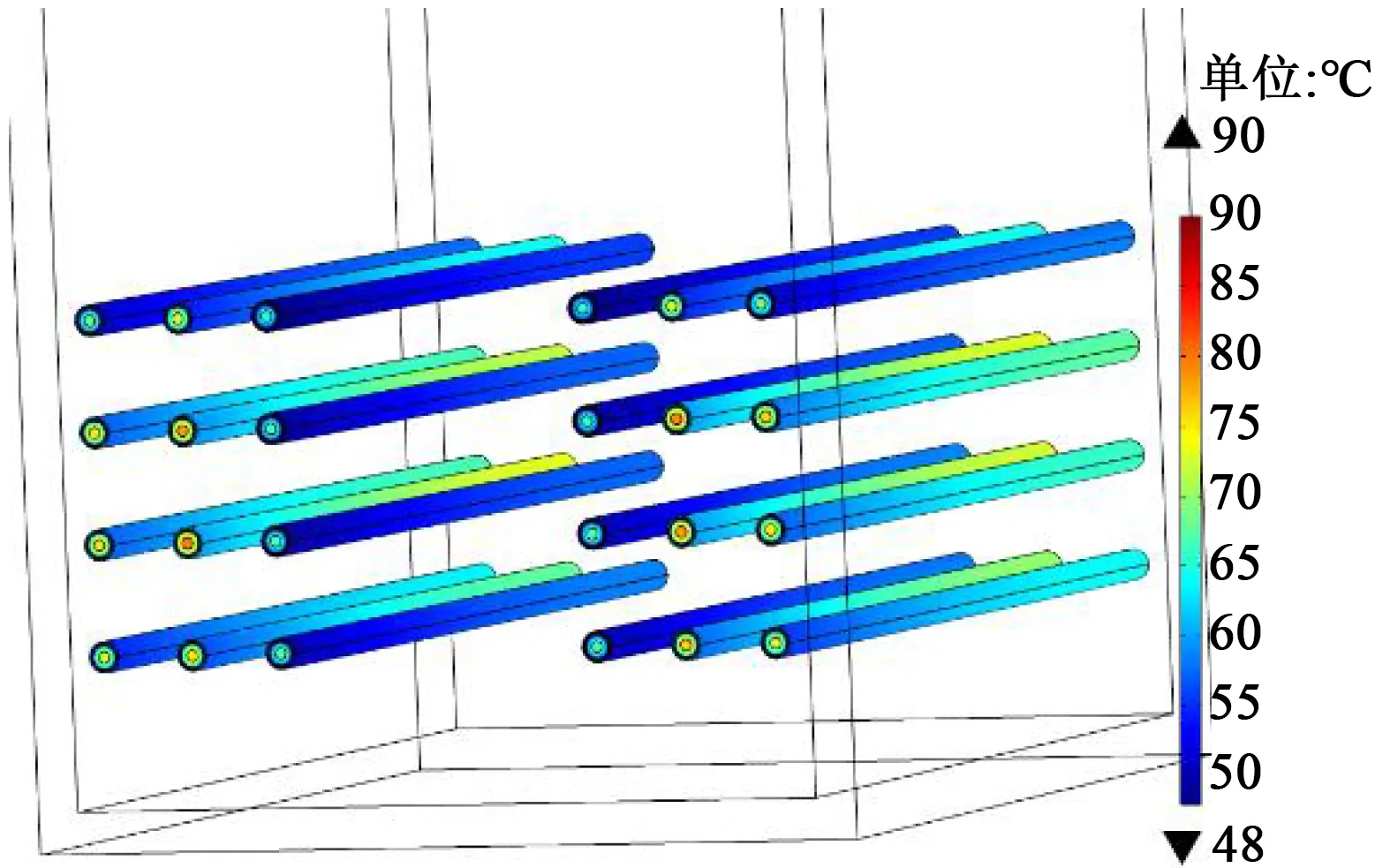
图10 隧道内电缆表面温度分布Fig.10 Cable surface temperature distribution in tunnel

图11 电缆轴向温度曲线Fig.11 Cable axial temperature curves
根据隧道建设相关规定,隧道敷设电缆安全口间距不应大于70 m,隧道内通风口长度与电缆载流量的关系曲线如图12所示。由图12可以看出,电缆载流量随着通风口长度的增加而降低,通风口间距较大会造成电缆散发的热量沿电缆径向不断堆积,使某段电缆温度过高,从而制约整条电缆载流量,因此通风口长度也是影响电缆载流量的重要因素。

图12 通风口长度对电缆载流量影响曲线Fig.12 Influence curve of vent length on the current carrying capacity of cable
2.5 设计正交试验
本节通过设计正交试验判断通风口长度、隧道内空气流速、流入隧道内空气温度和水平排列间距4种因素对电缆载流量的影响程度,为实际电缆隧道敷设工程提供理论依据以及合理化建议。
正交试验作为一种研究多因素多水平的设计方法,具有分布均匀性和整齐可比性等特点,每个因素之间存在交互作用,讨论某个因素时,不论因素水平为何值,仅分析极差便可判断它影响程度的大小[16]。通过设计相对应的正交表格,能够研究多因素高水平的科学试验方法。一般正交表表示为Ln(rm),其中n为试验次数(即正交表的行数),r为正交试验中因素的水平数,m为试验中的因素个数(即正交表的列数)。
以载流量为目标函数,选取4个影响因素:隧道内通风口长度、空气流速、流入隧道内空气温度、水平排列间距。试验因素水平根据隧道敷设电缆实际工程数据以及工作人员长期经验数据进行选择,数据如表4所示。

表4 试验因素水平表Tab.4 Test factor level table
本文中设计方案为4个因素,3个水平,选用L9(34)正交表,共需要进行9次试验,试验方案如表5所示。

表5 试验方案Tab.5 Experimental schemes
经过9次试验,试验结果分析如表6所示,表6中Kij为j列中第i对应的指标值之和,极差R可通过某一列中K1j、K2j、K3j的各个平均值中的最大值与最小值之差近似计算,极差R值的大小代表某种因素对结果影响程度的大小,R值越大,表示对结果的影响程度越大。

表6 试验数据统计Tab.6 Test data statistics
在表5中进行了9次仿真计算,并由仿真计算结果,计算了4种影响因素的极差。由计算的极差值能够看出,4种因素影响程度由大到小依次为隧道内空气流速、电缆的水平排列间距、通风口长度、流入隧道空气温度。因此在实际电缆隧道建设中,应将隧道内通风作为首要考虑的因素,由于隧道空气强制对流换热,能够快速带走电缆产生的热量,可近似认为隧道内空气温度为某定值,因此流入隧道空气温度相比其他3种因素其影响程度最低。
3 结论
(1)空气流速对电缆载流量的影响程度最大,通过布置风机系统增大隧道内空气流速,以此来提高隧道内电缆载流量,同时注意减少障碍物增大空气流动通道。
(2)在进行隧道电缆布置时,水平排列比三角形排列的电缆载流量更高,可在载流量要求高的回路使用水平排列,载流量要求较低的回路使用三角形排列,以节约隧道内空间资源。对于水平排列的电缆,其排列间距可选择为电缆半径。
(3)冬季与夏季流入隧道空气温差较大,造成电缆载流量相差较大,在不同季节可通过调节风机系统风速或者装设制冷机降低流入空气温度,以达到适合的载流量。
(4)隧道电缆载流量的影响程度由大到小顺序依次为隧道内空气流速、电缆的水平排列间距、通风口长度、流入隧道空气温度。对于城市隧道通风口由于其成本和城市用地的限制,可在规定要求内适当增大通风口长度,并通过增大风速,增大电缆排列间距和降低流入隧道内空气温度来提高整个隧道内的电缆载流量。

