周期型控制结构汽车队列的干扰抑制特性*

杨秀建，殷新雨，高 晋

（昆明理工大学交通工程学院，昆明 650500）

前言

汽车队列是指由若干辆汽车组成且能按照指定的控制策略规范有序成组运行的车队。队列中的车辆通过车载雷达、车-车通信获取前车的运动状态作为自车的控制输入。汽车队列通过合理的跟驰控制，可以显著缩小车间距，对缓解交通拥堵、保证交通安全、提升运输效率、降低能耗等方面都有积极的作用［1-3］。

国内外研发人员对汽车队列做了大量的研究工作，其中研究探讨较早较多的一个方面是从多智能体系统、群集系统或网络控制系统的角度研究队列的控制理论，多专注于队列的信息流拓扑、队形结构、队列稳定性、可扩展性、干扰抑制等方面的指标特性［4-12］。另一方面，随智能交通系统研究的深入，一些学者关注汽车队列在改善交通流方面的应用，试图在传统交通流中渗入部分车辆队列，以期改善交通流特性，缓解交通拥堵［13-16］。对交通流的改善，实质上是对交通波的抑制问题，文献［15］和文献［16］中将汽车队列与人工驾驶车辆组成的混合交通流跟驰模型视作控制系统，分别推导人工驾驶车辆到汽车队列以及汽车队列到人工驾驶车辆的传递函数，进而组合成混合交通流传递函数，并以此导出稳定性判别条件。这种方法实际上是通过局部节点车辆的误差传递特性得出整个交通流的误差传递特性，由于无法直接对整个队列进行建模处理，在应用上有一定的局限性。

在交通流问题研究中，一种处理方法是将交通流等效成质量-弹簧-阻尼系统［13］，交通波的抑制问题就等效为质点振动的抑制问题。振动抑制是一个专门领域的问题，相关的理论方法很多，这里不做过多的评述。其中，通过周期性结构抑制波的传递是振动抑制的一种思路，通过合理设计周期性结构就能在内部产生阻带，某些频率的波通过阻带时振幅会降低，从而达到抑制波传递的效果［17-20］。本文中从这一思路出发，尝试通过队列节点车辆控制增益的周期设置达到“周期性结构”的效果，以期实现对某些频率范围的交通波进行抑制。这一问题的研究须从整个汽车队列进行考虑，为便于分析将交通波的抑制等效成对干扰引起的车辆跟驰误差的抑制。在汽车队列干扰抑制研究方面，文献［5］中建立了队列各节点车辆的控制输入干扰到各节点车辆跟驰误差的传递函数关系，通过考察传递函数矩阵的最大奇异值来评价队列的干扰抑制特性。该方法的优点是队列内所有车辆自身的物理属性、队形结构、控制增益等对干扰抑制的影响都集中体现在误差传递矩阵中，基于这一思路，分析外界干扰和前方车辆扰动产生的跟驰误差沿周期型控制结构汽车队列的传播特性与干扰抑制特性。

1 周期型控制结构汽车队列建模

本文不考虑车-车通信，队列中各车辆仅通过车载雷达探测与其最近前方车辆的车间距、相对速度等信息进行跟驰控制，作为周期型控制结构汽车队列的初步研究探讨，主要考虑“…-K1-K2-K1-K2-K1-…”型简单的控制增益周期设置结构，如图1所示，其中K1、K2分别为相邻两辆车的控制增益组，分别又具体包含间距误差及其变化率的控制增益，即（kp1，kv1）和（kp2，kv2），整个车辆队列的控制原理可以按照如图2所示的质量-弹簧-阻尼等效机械系统模型来理解。

图1 周期型控制结构队列示意图

图2 周期型控制结构汽车队列等效机械模型

队列车辆采用定时距跟驰控制策略，第i辆车的期望车间距为di=hwvi(t)+δd，其中hw为车头时距，δd为静态车间距。因此，t时刻第i辆车的间距跟驰误差可表示为

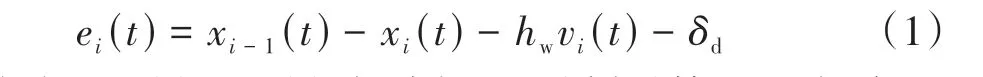
式中：xi-1（t）和xi（t）分别表示t时刻时第i-1辆车以及第i辆车的位移；vi（t）为第i辆车的速度。采用PD控制策略，则第i辆车的控制输入为

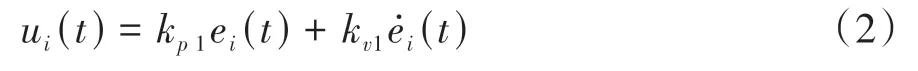
同理，第i-1辆车的控制输入为

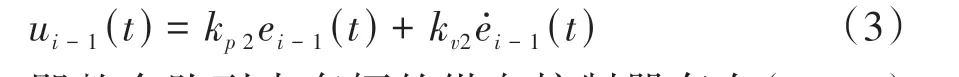
即整个队列中车辆的纵向控制器存在（kp1，kv1）和（kp2，kv2）两组控制增益，相邻的两辆车分别采用这两组增益，因此在上层控制层面形成了以两辆车为一个周期的周期型控制结构，队列中各车辆的控制输入为

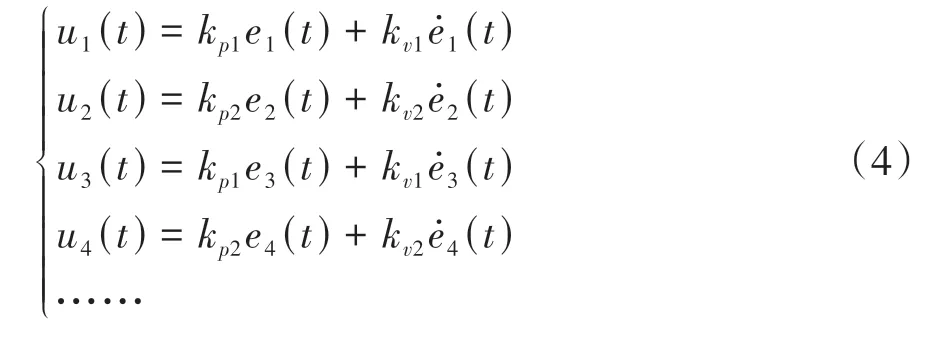
2 误差传播动力学

2.1 跟驰误差建模

考虑执行器响应延迟，用τ表示响应时间常数，则第i辆车的运动方程可表达为

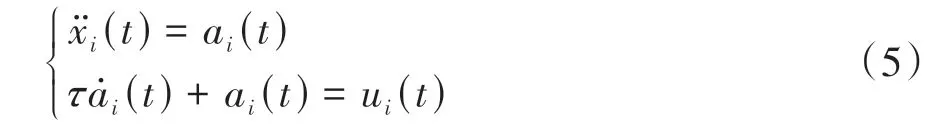
式中ai（t）为车辆i的加速度响应。联立式（5）中两式并进行拉氏变换，令初始条件为零，可得从控制输入ui（t）到位移响应xi（t）的传递函数模型：

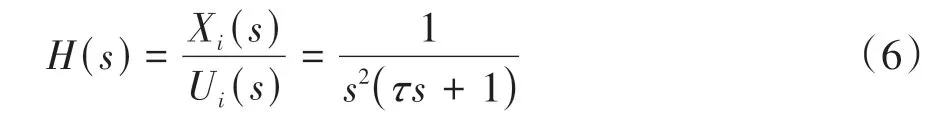
考虑初始位移和初始速度的影响，车辆i位移的拉氏变换为

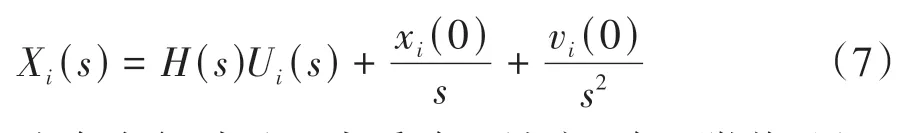
汽车在行驶过程中受路面坡度、路面附着、风阻等因素的影响，车辆实际产生的加速度可能并不能达到期望的加速度值，这里将实际加速度跟踪期望加速度的误差用Di（s）表示，即外部干扰引起的加速度增量。假设队列中每辆车的初始速度为零，即vi(0)=0，且相邻两车初始间距为δ，假设x0(0)=0，则第i辆车的初始位置为xi(0)=-iδ，式（7）可进一步写为

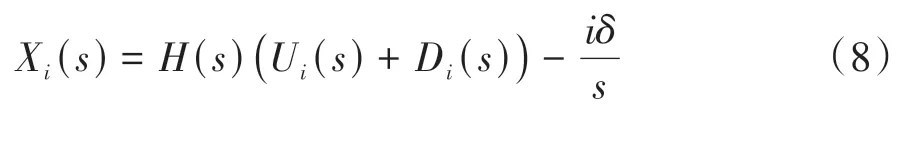
同理，对第i-1辆车，有

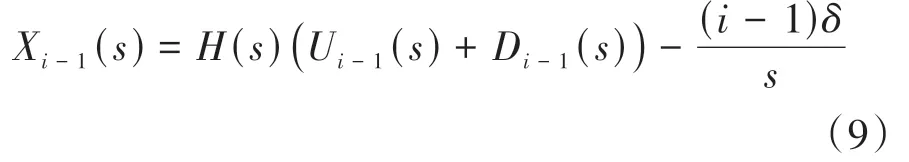
对式（1）间距跟驰误差进行拉氏变换得

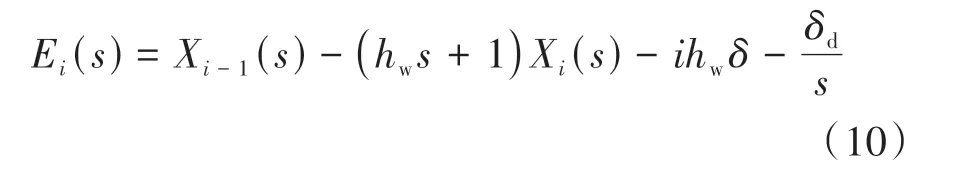
当i=1时，有

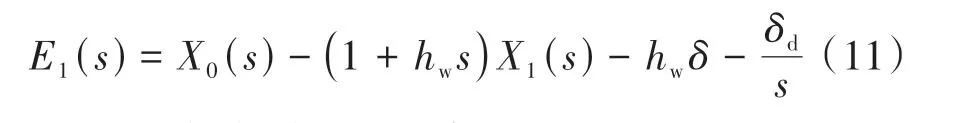
对式（2）控制输入进行拉氏变换得

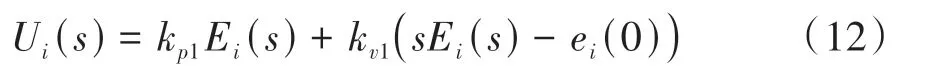
假设初始间距误差为0，即ei(0)=0，则

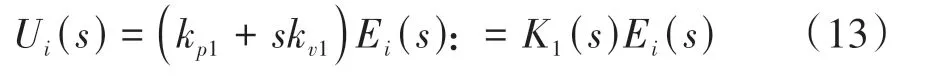
考虑本文探讨的周期型控制结构，有

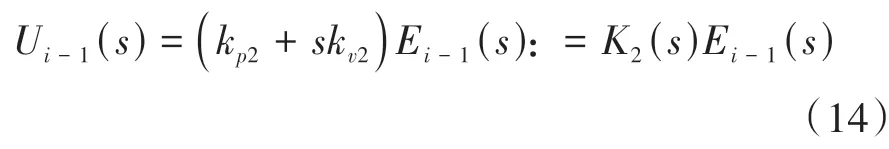
相应地，K1(s)=kp1+skv1，K2(s)=kp2+skv2。

将式（8）和式（13）代入式（11），并令δ=δd，得i=1时的跟驰误差传递关系：

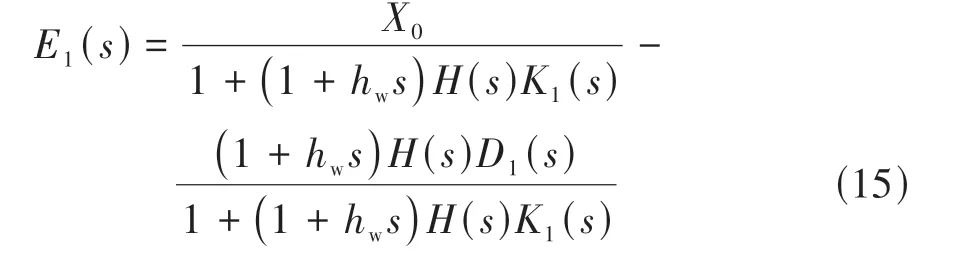
将式（8）和式（9）代入式（10），并令δ=δd，得到

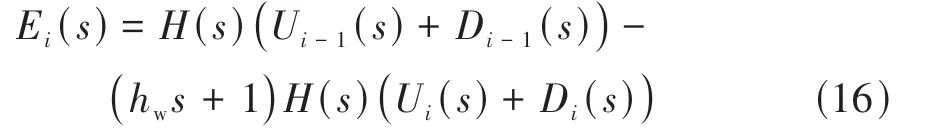
将式（13）与式（14）代入式（16）得车辆i的跟驰误差传递关系：

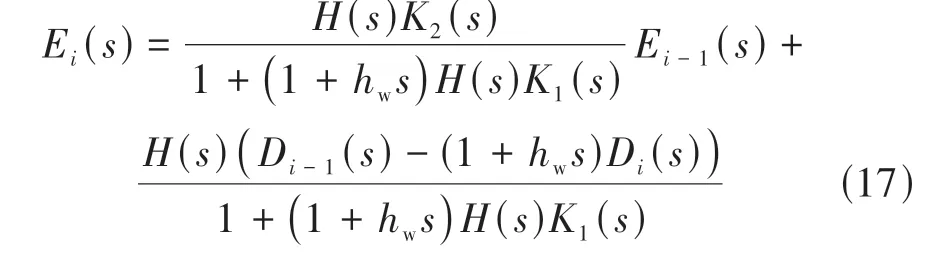
令

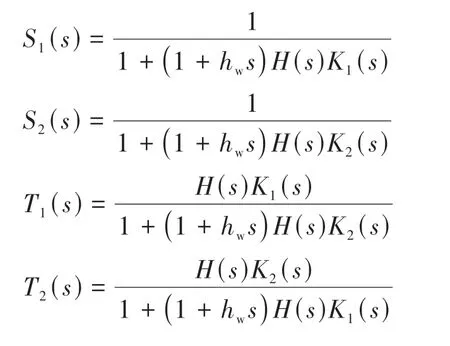
从而，误差传递关系可重写为

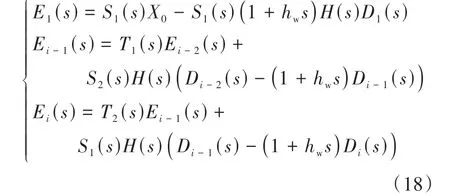
式中T1(s)和T2(s)为相应车辆的误差传播的传递函数。可以看出，由于采用周期型控制结构，一个周期内的两辆车有不同的跟驰误差传递函数。

2.2 误差传递函数矩阵

由式（18）可以看出，队列中车辆在行驶过程中导致间距误差的外界干扰是互相耦合的，本车的跟驰误差不但与前车的跟驰误差有关，还与本车及前车受到的外界干扰有关。

根据前文推导的误差传递关系，整个队列的间距误差方程可表达为

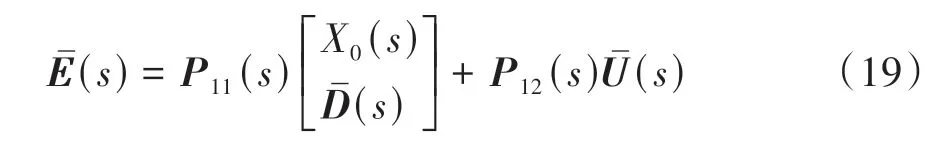
其中：

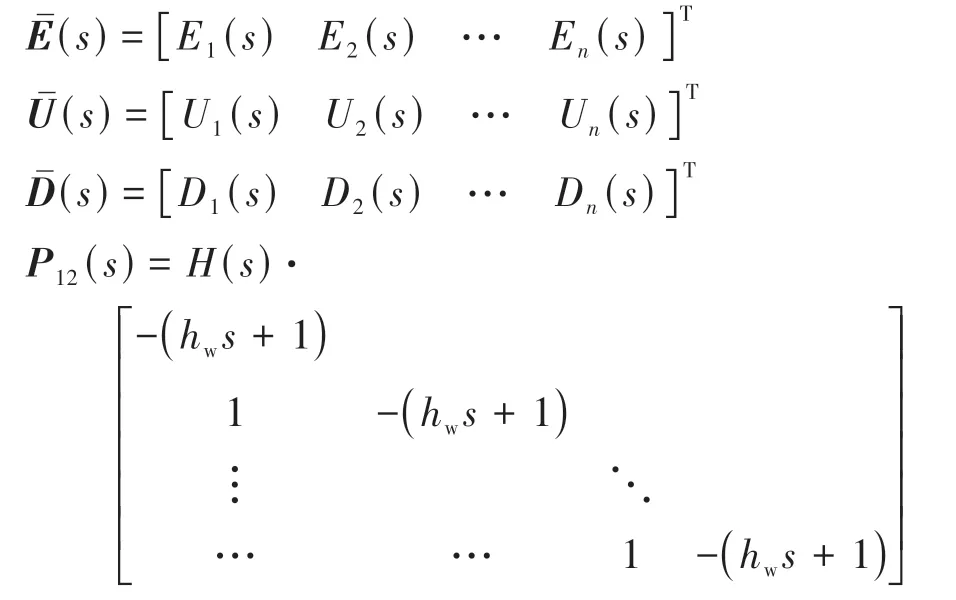
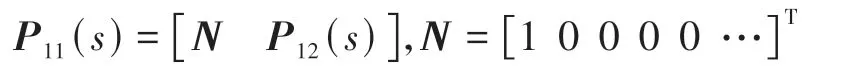
由式（13）和式（14），车辆加速度输入矩阵可写为

其中

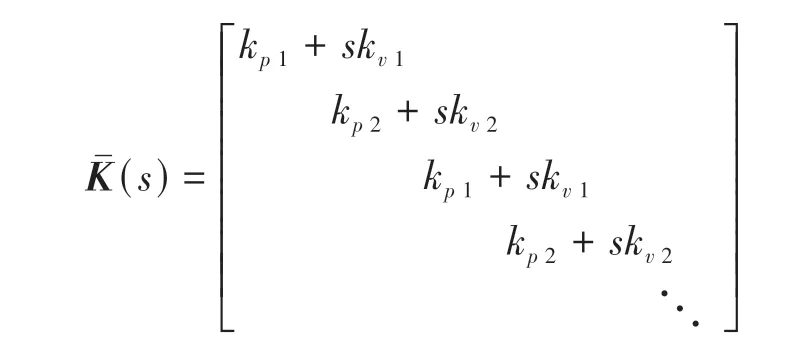
联立式（19）和式（20）得干扰到间距误差的传递关系方程为

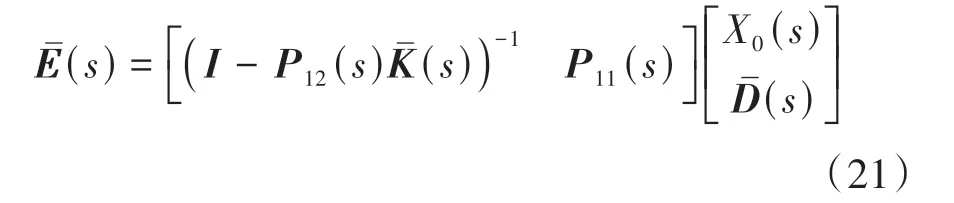
则有

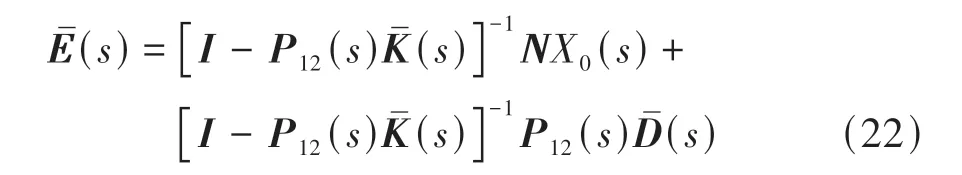
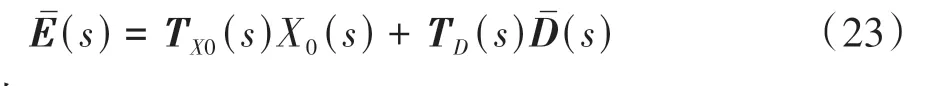
其中：

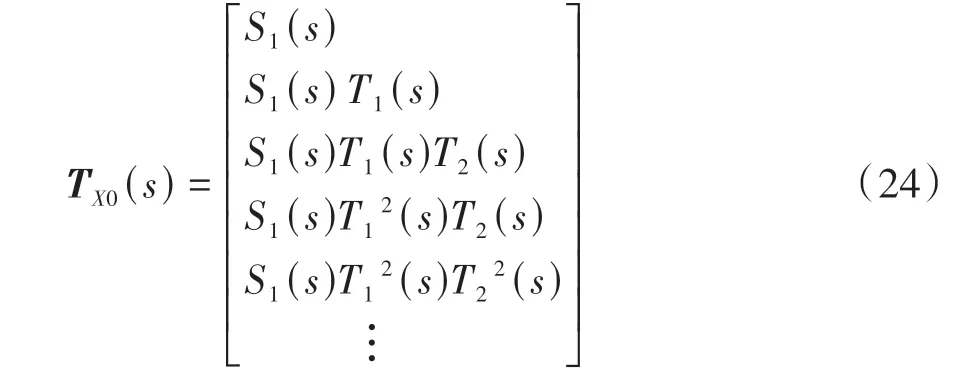
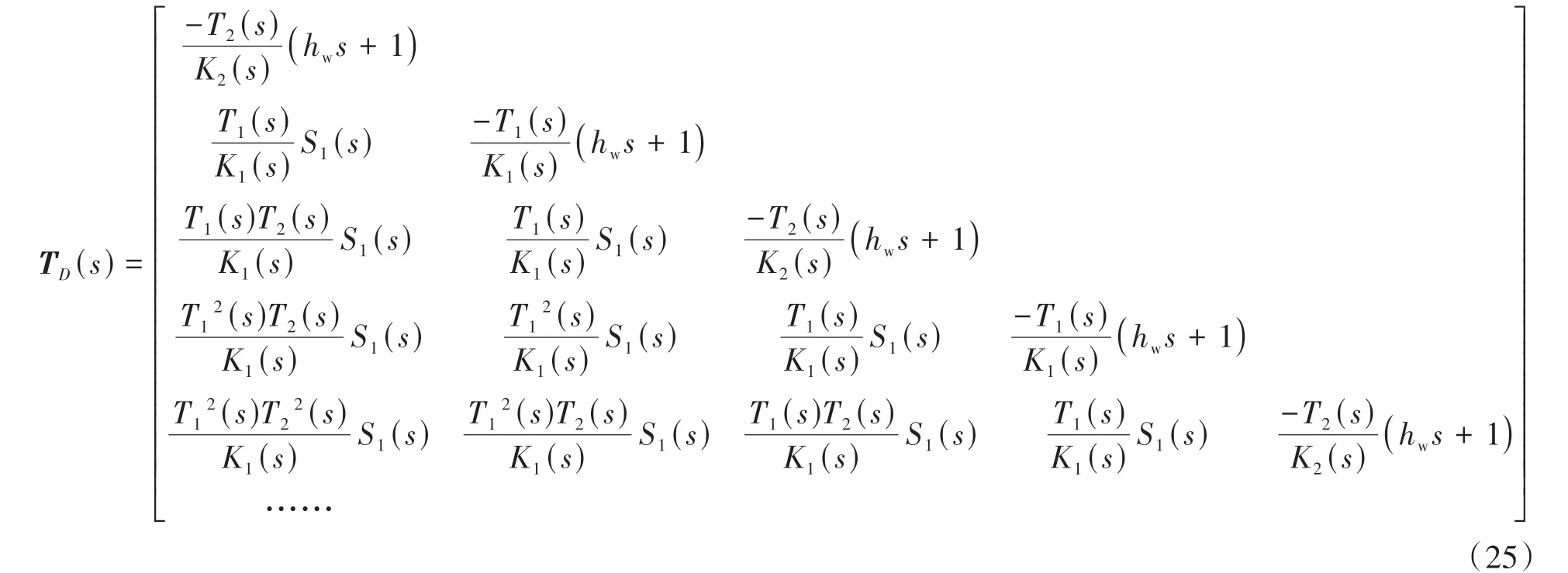
式中TD(s)、TX0(s)分别为外界干扰和领航车位移扰动到间距误差的传递函数矩阵，实际上TD(s)、TX0(s)可以认为是间距误差对外界干扰和领航车位移扰动的灵敏度函数矩阵，下面将通过灵敏度矩阵分析周期型控制结构队列的干扰抑制特性。

3 结果分析

3.1 同质队列的干扰抑制性分析

首先定义灵敏度函数矩阵TD(s)、TX0(s)的最大奇异值，分别用表示，由于最大奇异值随角频率ω变化，进一步定义灵敏度函数矩 阵TD(s)、TX0(s)的∞范 数，即其 中

表示最大奇异值的上界。在下面的分析中，根据需要用灵敏度函数矩阵TD(s)、TX0(s)的最大奇异值或∞范数来表征间距误差对外界干扰和领航车扰动的灵敏度，最大奇异值或∞范数值大，说明间距误差对干扰的灵敏度大，干扰将导致较大的跟驰误差。

考虑由6辆车组成的车辆队列，首先考察控制增益kp、kv的影响，取hw=0.6 s，τ=0.1 s/rad，增益kp和kv的取值范围皆为与增益kp和kv之间的关系分别如图3和图4所示。由图3可知，kp的影响相对而言更大一些，尤其是在kp显著较小时，无论kv如何取值的值都会显著较大。而从图4可知，对而言，kv的影响更为显著，特别是在kv>1时的值基本上都在1左右，不随kp、kv的变化而产生较大波动。

图3 控制增益kp和kv对‖ TD(s)‖∞的影响

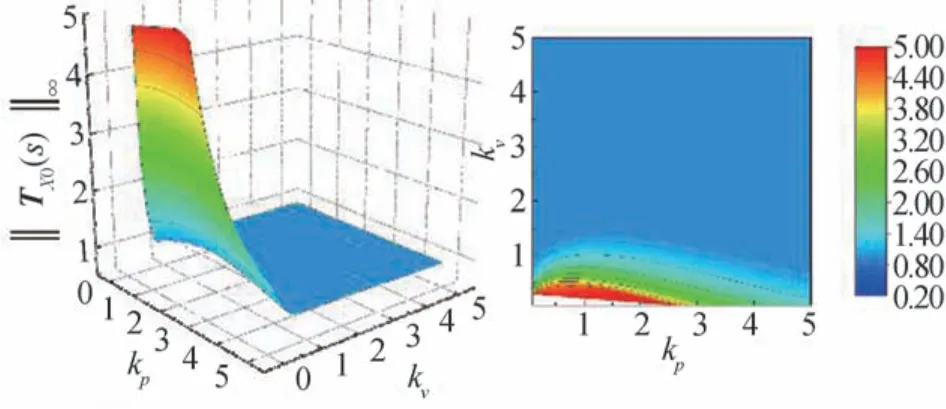
图4 控制增益kp和kv对‖ TX0(s)‖∞的影响

为进行周期控制结构分析，首先在‖TD(s)‖∞值为1的附近取对应的kp、kv增益值，表1给出了5种不同的取值组合及对应的‖TD(s)‖∞值。为研究周期型控制结构增益的变化对队列干扰抑制特性的影响，首先将其中一组增益固定为kp1=1.7，kv1=1.4，这里将其标记为K1，再从表1中取另外一个kp、kv组合（标记为K2）与之构成周期型控制结构。不同组合下灵敏度函数矩阵TD(s)的最大奇异值变化如图5所示。图中K1K2表示由K1、K2这两种增益组成的周期型控制结构。可以看出，与单一控制增益相比，在合理的增益组合下周期型控制结构可以降低(TD(jω))的峰值，即可以减小间距误差对外界干扰的最大灵敏度，提升对外界干扰的抑制能力，如图5（a）和图5（d）所示。但当组成周期型控制结构的两组增益相差较小时，周期型控制结构与单一增益控制的情况相比优势不太明显，如图5（b）和图5（c）所示。

表1 kp和kv取值组合

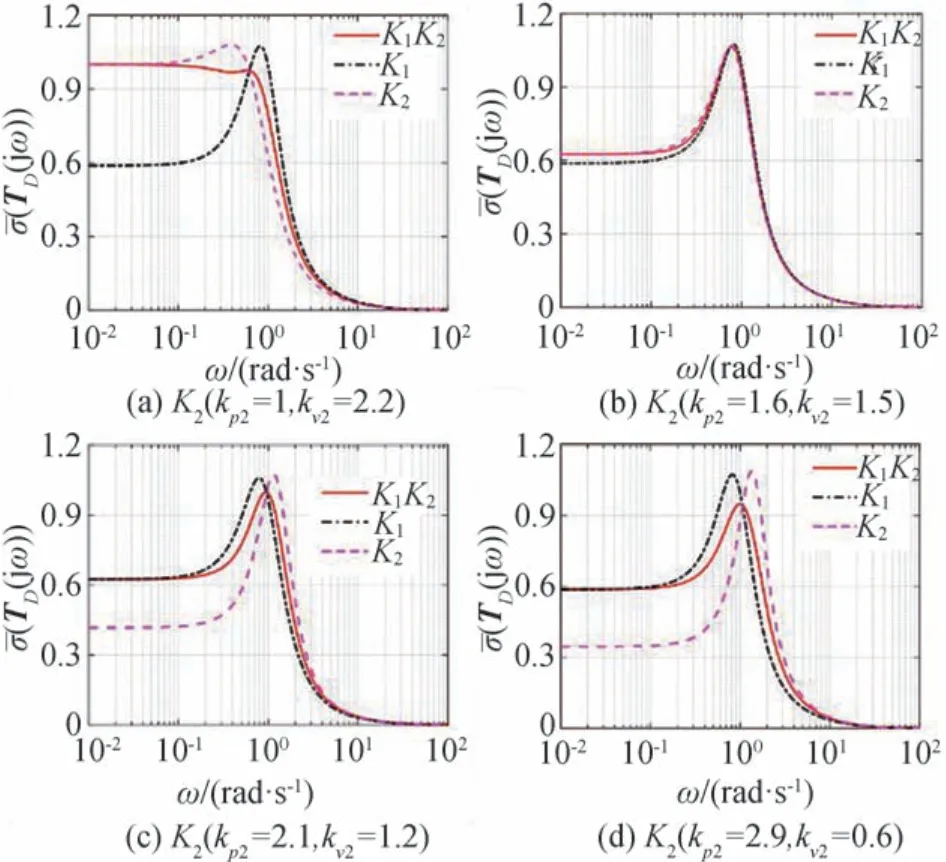
图5 不同增益组合的周期控制结构对(TD(jω))的影响

为避免结果的偶然性，分别在‖TD(s)‖∞值为2和3的附近另取对应的kp、kv增益组合，组成周期型控制结构，与单一控制增益相比对σˉ(TD(jω))的影响如图6所示。其中，图6（a）是在‖TD(s)‖∞值为2的附近选取对应的kp、kv增益组合，两组增益分别为K1：kp1=0.7，kv1=1.4；K2：kp2=2.1，kv2=0.5。图6（b）是在‖TD(s)‖∞值为3的附近选取的增益组合，两组增 益 分 别 为K1：kp1=0.7，kv1=1.0；K2：kp2=2.3，kv2=0.2。可以看出，与单一的增益控制相比，组成周期型控制结构可以显著降低σˉ(TD(jω))的峰值，从而可以显著降低跟驰间距误差对外界干扰的最大灵敏度，且对比图5和图6还可以发现，‖TD(s)‖∞值越大对应的kp、kv增益组合形成的周期型控制结构优势越明显。

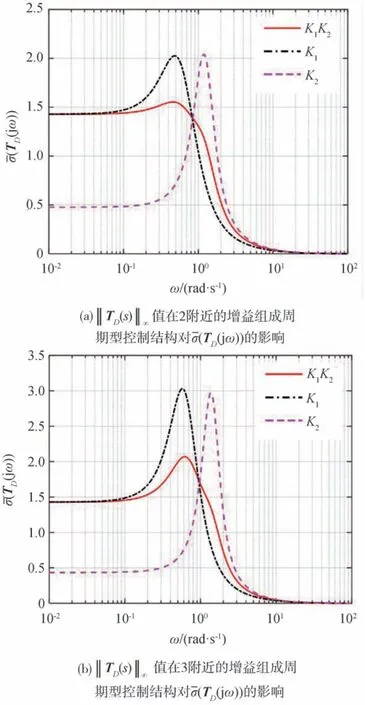
图6 ‖ TD(s)‖∞值在2和3附近的增益组成周期型控制结构对(TD(jω))的影响

从干扰到跟驰误差传递方程式（23）可知，汽车队列的间距跟驰误差不仅受行驶工况不确定性等外界干扰Dˉ(s)的影响，且与队列领航车的运动扰动X0(s)密切相关，因此下面继续考察周期型控制结构对领航车运动扰动灵敏度(TX0(jω))的影响。仍在‖TD(s)‖∞值为2和3的附近分别取两组对应的kp、kv增益组合，其中在‖TD(s)‖∞值为2附近取增益K1：kp1=0.7，kv1=1.4；K2：kp2=2.1，kv2=0.5。组成的周期型控制结构对领航车运动扰动灵敏度σˉ(TX0(jω))的影响如图7（a）所示；在‖TD(s)‖∞值为3附 近 取 增 益K1：kp1=0.7，kv1=1.0；K2：kp2=2.3，kv2=0.2。组成的周期型控制结构对灵敏度(TX0(jω))的影响如图7（b）所示。总体来看，在单一控制增益的情况下，不同的控制增益对灵敏度(TX0(jω))的影响差别很大，如图7中K1与K2的影响对比；而组成周期型控制结构后，虽然在‖TD(s)‖∞值较小时（如图7（a）‖TD(s)‖∞=2）不能完全优于所有的单一控制增益的情况，但基本上都可以保持较小的灵敏度值，特别是在‖TD(s)‖∞值较大时（如图7（b）‖TD(s)‖∞=3），周期型控制结构对降低灵敏度(TX0(jω))优势相对更明显。

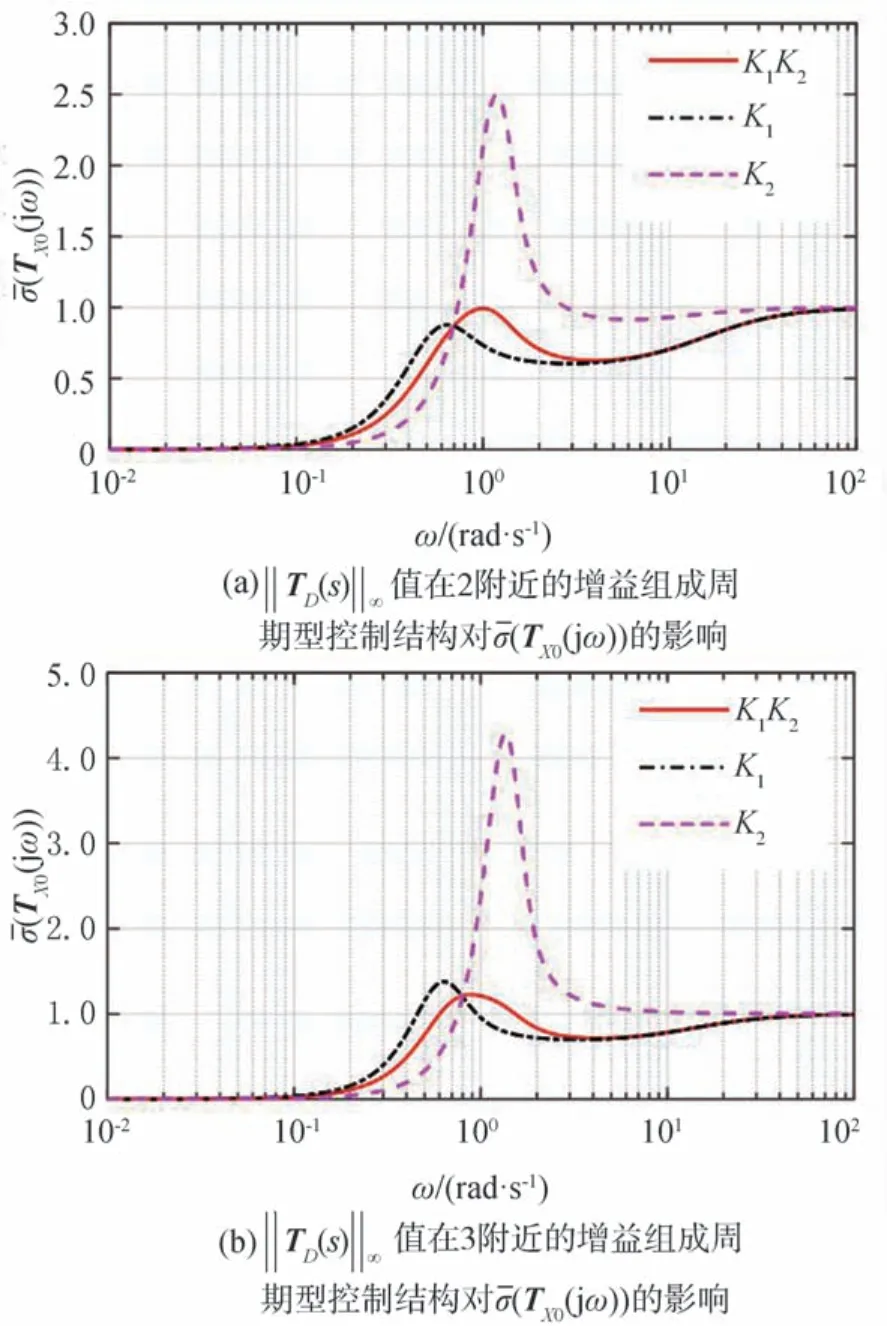
图7 ‖ TD(s)‖∞值在2和3附近的增益组成周期型控制结构对(TX0(jω))的影响

3.2 队列规模与干扰抑制分析

一般来说，汽车队列的规模越大控制越困难，对队列后方的车辆而言，既要承受外界干扰对自身的影响，又要受到前方各车辆运动扰动的影响，往往会产生更大的跟驰误差，队列的规模越大受到的影响越大。这里继续考察周期型控制结构对不同规模队列干扰抑制特性的影响。图8给出了‖TD(s)‖∞值在2附近对应的kp、kv增益组合形成的周期型控制结构对不同队列规模下(TD(jω))的影响，增益组合K1、K2与图7（a）的相同；图9给出了‖TD(s)‖∞值在3附近对应的kp、kv增益组合形成的周期型控制结构对不同队列规模下(TD(jω))的影响，增益组合K1、K2与图7（b）的相同。

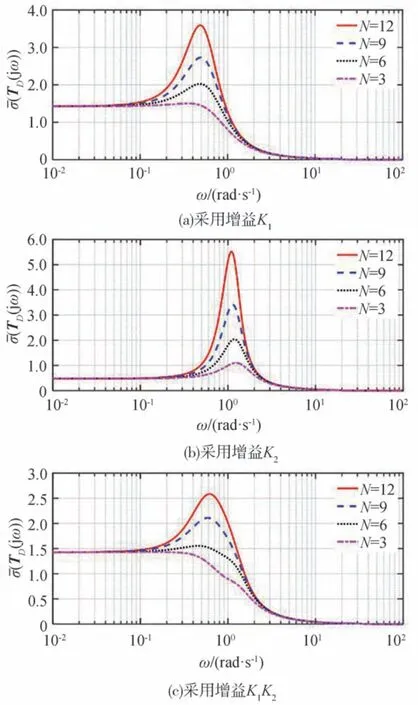
图8 ‖ TD(s)‖∞值在2附近的增益形成的周期型控制结构对不同队列规模下(TD(jω))的影响

综合图8和图9可以看出，在相同队列规模下单一控制增益组合成周期型控制结构后，(TD(jω))的峰值都要显著小于原单一控制增益的情况；采用单一控制增益时，随着队列规模的增加，(TD(jω))峰值增加的幅度越来越大，即队列的可扩展性较差，而将增益组合成周期型控制结构后随队列规模的增加(TD(jω))峰值增加的幅度越来越小，体现出较好的队列可扩展性。

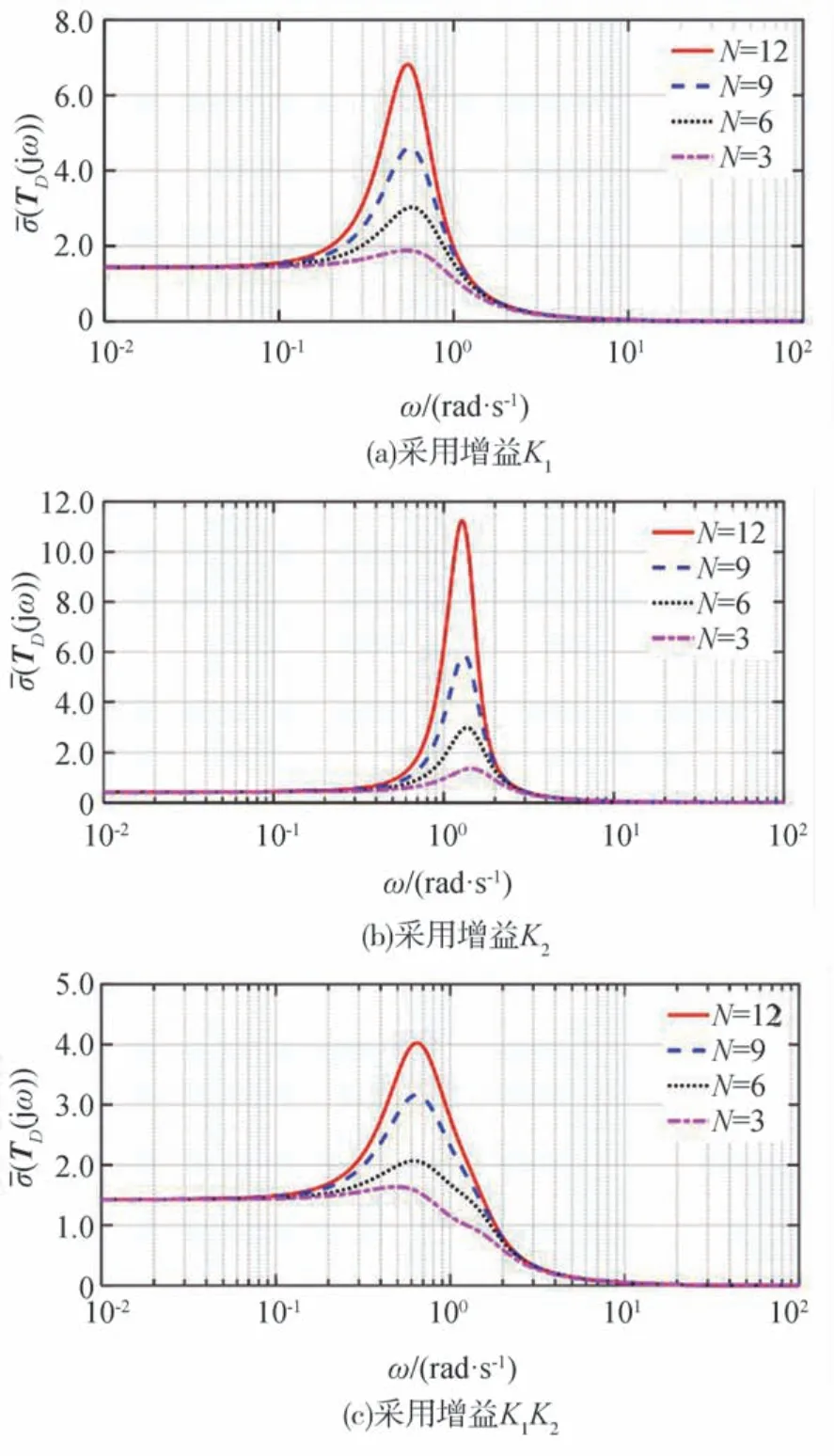
图9 ‖ TD(s)‖∞值在3附近的增益形成的周期型控制结构对不同队列规模下(TD(jω))的影响

3.3 异质队列的干扰抑制性分析

实际的汽车队列都是异质的，下面继续考察周期型控制结构对异质汽车队列的影响。考虑到车辆异质的复杂性，这里将车辆的异质性集中用车辆响应延迟时间常数τ来体现。考虑如图10所示的异质车辆队列，由3种不同时间常数的车辆组成，并假设τ1=0.1 s/rad，τ2=0.2 s/rad，τ3=0.3 s/rad。 在‖TD(s)‖∞值为2的附近取两组增益K1：kp1=1.0，kv1=1.2；K2：kp2=3.0，kv2=0.4。在‖TD(s)‖∞值为3的附近 取 两 组，即K1：kp1=1.0，kv1=0.9；K2：kp2=2.4，kv2=0.4。

图10 异质周期型控制结构队列示意图

周期型控制结构对异质车辆队列外界干扰灵敏度(TD(jω))的影响如图11所示。可以看出，与同质车辆队列的情况类似，周期型控制结构可显著减小间距跟驰误差对外界干扰灵敏度(TD(jω))的峰值，且‖TD(s)‖∞的值越大采用周期型控制结构的优势越明显。周期型控制结构对异质车辆队列领航车扰动灵敏度(TX0(jω))的影响如图12所示。可以看出，与同质车辆队列的情况类似，在单一控制增益情况下，不同增益对灵敏度(TX0(jω))的影响差别很大；组成周期型控制结构后基本上都可以保持较小的灵敏度值。

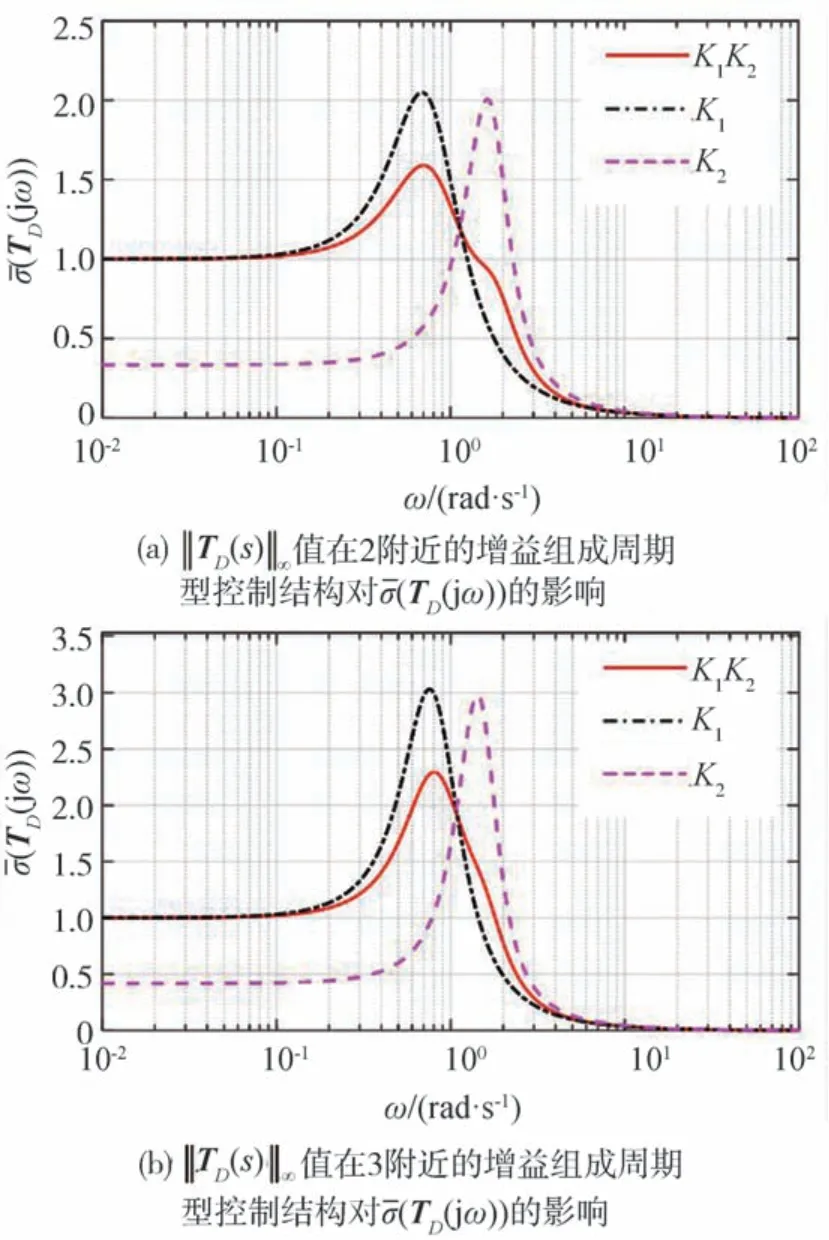
图11 周期型控制结构对异质车辆队列(TD(jω))的影响

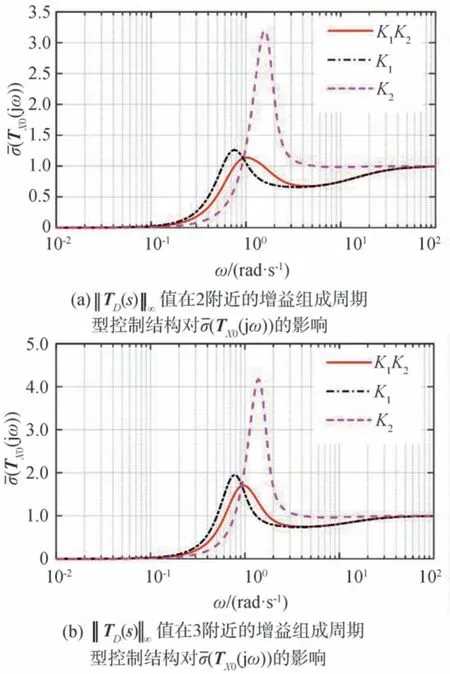
图12 周期型控制结构对异质车辆队列(TX0(jω))的影响

3.4 时域响应分析

基于Matlab/Simulink搭建由100辆车组成的同质车辆队列仿真模型，采用周期型控制结构和定时距跟驰控制策略。假设队列的初速度为20 m/s，初始加速度为0，静态车间距δd=10 m，车头时距hw=0.6 s，执行器延迟时间常数τ=0.1 s/rad，构成周期型控制结构的两组增益分别为K1：kp1=1.0，kv1=2.2；K2：kp2=2.9，kv2=0.6。仿真中在相应的车辆上施加加速度干扰，通过考察各车辆的间距跟驰误差来评价周期型控制结构的干扰抑制性能。

考察两种加速度干扰。第一种情况是在t=0时刻，在前10辆车上同时施加持续时间为4 s、峰值为0.5 m/s2的加速度干扰，如图13（a）所示。第二种情况，是在第10、20、30、40、50辆车上先后施加峰值为0.5 m/s2、持续时间为8 s的加速度干扰，干扰信号如图13（b）所示，其中在t=0时刻施加在第10辆车上，仿真30 s后即在t=30 s时刻在第20辆车上施加该干扰，持续时间仍为8 s，以此类推，在t为60、90、120 s时刻分别在第30、40、50辆车上依次施加该干扰。

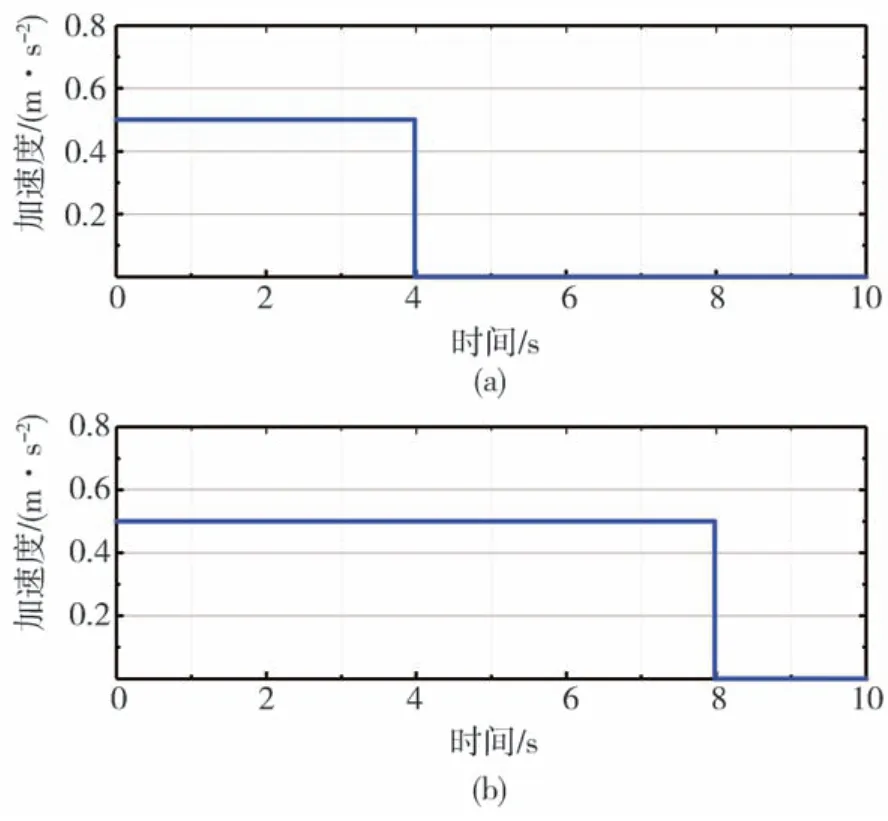
图13 加速度施加干扰信号

在两种干扰情况下仿真的第50、100、150 s时刻各车辆的间距跟驰误差响应分别如图14和图15所示。显然，采用周期型控制结构的汽车队列中各车辆都始终可以保持较小的间距跟驰误差，最大跟驰误差均小于5 m，且随着时间的推移，间距跟驰误差逐渐趋于零，队列趋于稳定，而采用单一控制增益的车辆队列在某些时刻相应车辆会出现相对较大的间距跟驰误差，最大误差达30 m，队列调整控制困难，难以趋于稳定。

图14 前10辆车施加干扰的间距跟驰误差响应

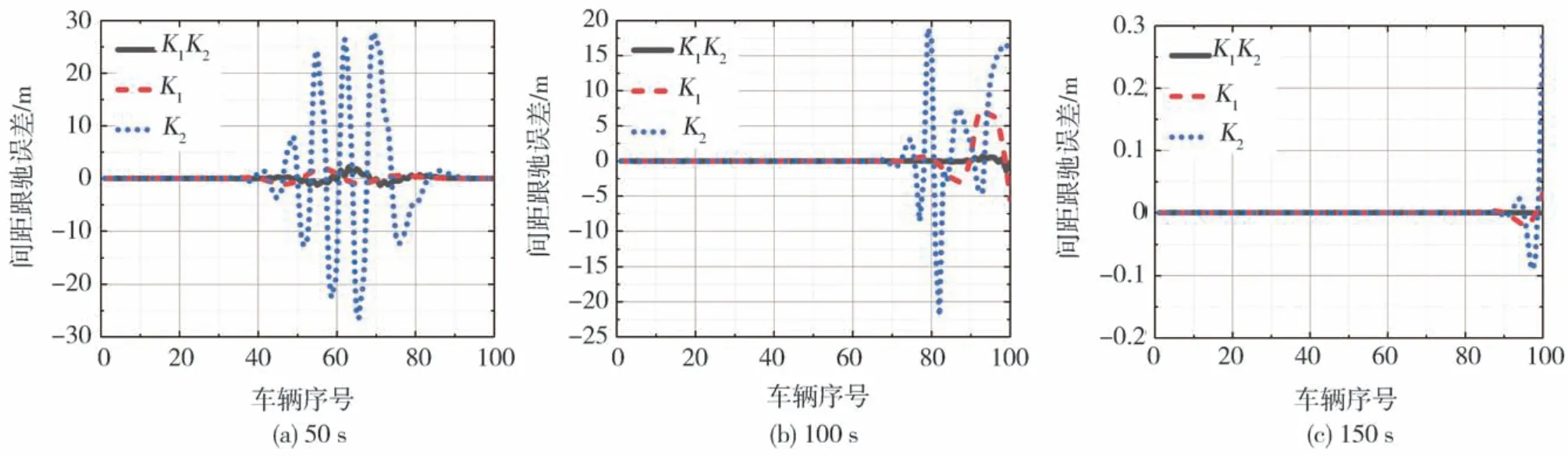
图15 第10、20、30、40、50辆车施加干扰的间距跟驰误差响应

4 结论

受周期性结构抑制振动的启发，针对汽车队列控制提出了周期型队列控制结构。推导了周期型控制结构汽车队列的干扰到间距跟驰误差的传递关系，通过间距误差传递函数矩阵分析了周期型控制结构汽车队列的干扰抑制特性，得到以下结论。

（1）周期型控制结构通过合理设计，可有效降低干扰到间距误差传递函数矩阵最大奇异值的峰值，即可有效降低干扰引起的最大间距跟驰误差，提升汽车队列的干扰抑制能力，且组成周期型控制结构的两组增益相差越大，对干扰的抑制能力越强，周期型控制结构的优势越明显。

（2）随着队列规模的增加，在单一增益控制间距跟驰误差增长幅度越来越大的情况下，组成周期型控制结构后间距误差的增长幅度逐渐衰减，体现出较好的队列可扩展性。

（3）考察了周期型控制结构对异质车辆队列的影响，通过执行器延迟时间常数来集中体现车辆的异质性。结果表明，周期型控制结构对异质车辆队列仍有较好的干扰抑制特性，总体影响与同质队列的情况类似。

周期型控制结构的形式并不是唯一的，作为初步研究本文主要考虑“…-K1-K2-K1-K2-K1-…”型增益大小周期变化的周期型控制结构，在后续的研究中还将继续探讨控制器结构及信息流拓扑结构周期变化等类型的周期型控制结构车辆队列，并深入研究各周期型控制结构车辆队列的干扰抑制机制等问题。